On the a posteriori estimates for inverse operators of linear parabolic equations with applications to the numerical enclosure of solutions for nonlinear problems

Abstract

We consider the guaranteed a posteriori estimates for the inverse parabolic operators with homogeneous initial-boundary conditions. Our estimation technique uses a full-discrete numerical scheme, which is based on the Galerkin method with an interpolation in time by using the fundamental solution for semidiscretization in space. In our technique, the constructive a priori error estimates for a full discretization of solutions for the heat equation play an essential role. Combining these estimates with an argument for the discretized inverse operator and a contraction property of the Newton-type formulation, we derive an a posteriori estimate of the norm for the infinite-dimensional operator. In numerical examples, we show that the proposed method should be more efficient than the existing method. Moreover, as an application, we give some prototype results for numerical verification of solutions of nonlinear parabolic problems, which confirm the actual usefulness of our technique.

1 Introduction

Setting $\fancyscript{L}_t:={\frac{\partial {}}{\partial {t}}}-\nu \triangle +b\cdot \nabla +c$, for $f \in L^2\bigl (J;L^2(\varOmega )\bigr )$, consider the following linear parabolic partial differential equations (PDEs) with homogeneous initial and boundary conditions:

where $\varOmega \subset \mathbb R ^d$, $(d\in \{1,2,3\})$ is a bounded polygonal or polyhedral domain, $J:=(0,T)\subset \mathbb R$, $(T<\infty )$ is a bounded interval, $\nu$ is a positive constant, $b \in L^\infty \bigl (J;L^\infty (\varOmega )\bigr )^d$, and $c \in L^\infty \bigl (J;L^\infty (\varOmega )\bigr )$. As is well known, for any $f \in L^2\bigl (J;L^2(\varOmega )\bigr )$, there exists a unique weak solution $u \in L^2\bigl (J;H_0^1(\varOmega )\bigr )$ to the problem (1). Denoting the solution operator of (1) by $\fancyscript{L}_t^{-1}$, it is a bounded linear operator from $L^2\bigl (J;L^2(\varOmega )\bigr )$ to $L^2\bigl (J;H_0^1(\varOmega )\bigr )$.

The main aim of this paper is to obtain the concrete value $C_{L^2L^2,L^2H_0^1}>0$ satisfying the following estimates:

$$\begin{aligned} \left\| {{{\fancyscript{L}}}_t^{-1}}\right\| _{{\fancyscript{L}} \bigl (L^2(J;L^2(\varOmega )),L^2(J;H_0^1(\varOmega ))\bigr )} \le C_{L^{2}L^{2},L^{2}H_{0}^{1}}. \end{aligned}$$

(2)

The constant $C_{L^2L^2,L^2H_0^1}$ plays an important role in the verification of solutions for the initial-boundary-value problems for the nonlinear parabolic PDEs, and we usually need to estimate it as small as possible. The concrete value $C_{L^2L^2,L^2H_0^1}>0$ satisfying (2) can be calculated by the Gronwall inequality or other theoretical considerations (e.g., [16]), which we call the “a priori estimates.” However, in general, $C_{L^2L^2,L^2H_0^1}$ obtained by such a priori estimates is exponentially dependent on the length of the time interval $J$ unless the corresponding elliptic part of the operator $\fancyscript{L}_t$ is coercive [4, 5]. Thus a priori estimates often lead to an overestimate for the norm of $\fancyscript{L}_t^{-1}$, which yields worse results for some purposes.

In order to overcome this difficulty, we proposed a method to calculate $C_{L^2L^2,L^2H_0^1}$ by numerical computation with guaranteed accuracy in [10], which we called “a posteriori estimates.” The method is based on combining the a priori error estimates for a semidiscretization with the a priori estimates for the ordinary differential equations (ODEs) in time. It has proven to be more efficient than the existing a priori method; some numerical examples show that this a posteriori method can remove the exponential dependency on the time interval $J$. However, it has a very large computational cost, because the semidiscretization of (1) causes stiff ODEs that require a very small step size. Also, it is not clear what time-space ratio to use in the discretization process.

In this paper, we propose a new a posteriori method with a fully discretized Newton-type operator, which uses the Galerkin approximation in the space direction and the Lagrange-type interpolation in the time direction. In the case of the simple heat equations, some fundamental properties (e.g., the stability and a priori error estimates) for this full-discretization scheme have already been obtained in [11]. In the desired estimation of the inverse operator norm $\left\| {\fancyscript{L}_t^{-1}}\right\| _{\fancyscript{L}\left( L^2(J;L^2(\varOmega )),L^2(J;H_0^1(\varOmega ))\right) }$, the matrix norm estimates corresponding to the discretized inverse operator and the constructive error analysis for the simple heat equations are important and essential. By constructive analysis, we can also guess an appropriate time-space ratio prior to the actual computation. Moreover, by using numerical examples, we will show that the proposed method succeeds in obtaining a posteriori estimates with less computational cost than the previous method in [10]. This means that the present method is very robust compared with the previous one.

The contents of this paper are as follows: In Sect. 2, we introduce some function spaces, operators, and other notation. In Sect. 3, we introduce the results of stability and a priori error estimates for the full-discretization scheme for the simple heat equations, which were obtained in [11]. In Sect. 4, we consider the approximate quasi-Newton operator that corresponds to the full-discretization scheme for problem (1). In Sect. 5, we derive the new a posteriori estimates of (2) by combining the results in Sect. 3 with the property of the approximate quasi-Newton operator defined in the previous section. In Sect. 6, we compare the computed values for $C_{L^2L^2,L^2H_0^1}$ by three methods, namely, the a priori method, the a posteriori estimates in [10], and the new a posteriori method obtained in Sect. 5. In this section we also show some prototype results of the numerical enclosure of solutions for nonlinear parabolic problems as an application of our method.

2 Notation

In this section, we introduce some function spaces, operators, and other notation. Let $L^2(\varOmega )$ and $H^1(\varOmega )$ be the usual Lebesgue and Sobolev spaces on $\varOmega$, respectively, and define the natural inner product of $u$, $v$ in $L^2(\varOmega )$ by $\left( u,v\right) _{L^2(\varOmega )}:=\int _\varOmega u(x)v(x)\,dx$. Also, let $H_0^1(\varOmega )$ be a Sobolev space defined by $H_0^1(\varOmega ):={\left\{ {u \in H^1(\varOmega )\!}~;~{u = 0 \ \mathrm{on } \ \partial \varOmega }\right\} }$ with inner product $\left( u,v\right) _{H_0^1(\varOmega )}:=\left( \nabla u,\nabla v\right) _{L^2(\varOmega )^d}$. We will sometimes refer to the following Sobolev inequality on $H_0^1(\varOmega )$. Namely, for a suitable constant $p \ge 1$, which is dependent on the dimension of $\varOmega$, there exists a constant $C_{s,p}>0$ such that

$$\begin{aligned} \left\| {u}\right\| _{L^p(\varOmega )}&\le C_{s,p}\left\| {u}\right\| _{H_0^1(\varOmega )}, \quad \forall u\in H_0^1(\varOmega ). \end{aligned}$$

(3)

When $p=2$, (3) is called the Poincaré inequality.

Let $\triangle :L^2(\varOmega ) \rightarrow L^2(\varOmega )$ be the Laplace operator that is self-adjoint on the domain $D(\triangle ):=\left\{ u \in H_0^1(\varOmega );\triangle u \in L^2(\varOmega )\right\}$. Let $V^1(J)$ be a subspace of $H^1(J)$ defined by $V^1(J):=\left\{ u \in H^1(J); u(0) = 0\right\}$. Then, $V^1(J)$ is a Hilbert space with inner product $\left( u,v\right) _{V^1(J)}:=\left( u^\prime ,v^\prime \right) _{L^2(J)}$. The time-dependent Lebesgue space $L^2\bigl (J;L^2(\varOmega )\bigr )$ is defined as a space of square-integrable $L^2(\varOmega )$-valued functions on $J$. Then, $L^2\bigl (J;L^2(\varOmega )\bigr )$ is a Hilbert space with inner product $\left( u,v\right) _{L^2(J;L^2(\varOmega ))}:=\int _J\int _\varOmega u(x,t)v(x,t)\,dxdt$. We denote the function space $L^2\bigl (J;L^2(\varOmega )\bigr )$ as $L^2L^2$, for short. Let $L^2\bigl (J;H_0^1(\varOmega )\bigr )$ be a subspace of $L^2L^2$ defined by

$$\begin{aligned} L^2\bigl (J;H_0^1(\varOmega )\bigr ):={\left\{ {u \in L^2L^2\!}~;~{\nabla u \in L^2\bigl (J;L^2(\varOmega )\bigr )^d,~u(\,\cdot \,,t)=0 \quad \mathrm{on }\quad \partial \varOmega , \,\mathrm{a.e. }\, t \in J}\right\} }. \end{aligned}$$

Then, $L^2H_0^1 \equiv L^2\bigl (J;H_0^1(\varOmega )\bigr )$ is a Hilbert space with inner product $\left( u,v\right) _{L^2H_0^1}:=\left( \nabla u,\nabla v\right) _{(L^2L^2)^d}$. Let $V^1\bigl (J;L^2(\varOmega )\bigr )$ be a subspace of $L^2L^2$ defined by

$$\begin{aligned} V^1\bigl (J;L^2(\varOmega )\bigr ):={\left\{ {u \in L^2\bigl (J;L^2(\varOmega )\bigr )\!}~;~{{\frac{\partial {u}}{\partial {t}}} \in L^2\bigl (J;L^2(\varOmega )\bigr ),~u(\,\cdot \,,0)=0 \quad \mathrm{in }\quad L^2(\varOmega )}\right\} }. \end{aligned}$$

Then, $V^1L^2 \equiv V^1\bigl (J;L^2(\varOmega )\bigr )$ is a Hilbert space with inner product $\left( u,v\right) _{V^1L^2}:=\left( {\frac{\partial {u}}{\partial {t}}},{\frac{\partial {v}}{\partial {t}}}\right) _{L^2L^2}$. We define the Hilbert space $V:=V^1L^2 \cap L^2H_0^1$ with inner product $(u,v)_V := \left( u,v\right) _{V^1L^2} + \left( u,v\right) _{L^2H_0^1} = \left( {\frac{\partial {u}}{\partial {t}}},{\frac{\partial {v}}{\partial {t}}}\right) _{L^2L^2} + \left( \nabla u,\nabla v\right) _{(L^2L^2)^d}$. Moreover, we define the partial differential operator $\triangle _t:L^2L^2 \rightarrow L^2L^2$ by $\triangle _t:={\frac{\partial {}}{\partial {t}}}-\nu \triangle$ on the domain $D(\triangle _t):=V^1L^2 \cap L^2\bigl (J;D(\triangle )\bigr )$. Then, the inverse of $\triangle _t$ exists (e.g., [3]), and we denote it by $\triangle _t^{-1} \in \fancyscript{L}(L^2L^2)$. Notably, the range of $\triangle _t^{-1}$ satisfies $R(\triangle _t^{-1})=D(\triangle _t)$. From the compactness of the embedding $I_e:D(\triangle _t) \hookrightarrow L^2H_0^1$, the bounded linear operator $I_e\triangle _t^{-1} \in \fancyscript{L}(L^2L^2,L^2H_0^1)$ is also compact.

Let $S_h(\varOmega )$ be a finite-dimensional subspace of $H_0^1(\varOmega )$ dependent on the discretization parameter $h$. For example, $S_h(\varOmega )$ is considered to be a finite element space with mesh size $h$. Let $n$ be the number of degrees of freedom of $S_h(\varOmega )$, and let $\{\phi _i\}_{i=1}^n \subset H_0^1(\varOmega )$ be the basis functions of $S_h(\varOmega )$. Moreover, we denote a vector of the basis functions of $S_h(\varOmega )$ by $\phi :=(\phi _1,\ldots ,\phi _n)^T$. We also assume the inverse estimates on $S_h(\varOmega )$ like as follows:

Assumption 2.1

There exists a positive constant $C_{\mathrm{inv}}(h)$ satisfying

$$\begin{aligned} \left\| {u_h}\right\| _{H_0^1(\varOmega )}&\le C_{\mathrm{inv}}(h)\left\| {u_h}\right\| _{L^2(\varOmega )}, \quad \forall u_h\in S_h(\varOmega ). \end{aligned}$$

(4)

For example, if $\varOmega$ is a bounded open interval in $\mathbb R$, and $S_h(\varOmega )$ is the P1 finite element space, then Assumption 2.1 is realized with $C_{\mathrm{inv}}(h)=\frac{\sqrt{12}}{h_{\min }}$, where $h_{\min }$ is the minimum mesh size in the division of $\varOmega$ (see e.g., [15, Theorem 1.5]).

Let $P_h^1:H_0^1(\varOmega ) \rightarrow S_h(\varOmega )$ be an $H_0^1$-projection. Namely, for an arbitrary element $u \in H_0^1(\varOmega )$, $P_h^1u \in S_h(\varOmega )$ satisfies the following variational equation:

$$\begin{aligned} \left( \nabla (u-P_h^1u),\nabla v_h\right) _{L^2(\varOmega )^d} = 0, \quad \forall v_h \in S_h(\varOmega ). \end{aligned}$$

(5)

We need the following assumptions as the a priori error estimates for $P_h^1$.

Assumption 2.2

There exists a positive constant $C_\varOmega (h)$ satisfying

$$\begin{aligned} \left\| {u-P_h^1u}\right\| _{H_0^1(\varOmega )}&\le C_\varOmega (h)\left\| {\triangle u}\right\| _{L^2(\varOmega )}, \quad \forall u\in D(\triangle ), \end{aligned}$$

(6)

$$\begin{aligned} \left\| {u-P_h^1u}\right\| _{L^2(\varOmega )}&\le C_\varOmega (h)\left\| {u-P_h^1u}\right\| _{H_0^1(\varOmega )}, \quad \forall u\in H_0^1(\varOmega ). \end{aligned}$$

(7)

For example, if $\varOmega$ is a bounded open interval in $\mathbb R$, and $S_h(\varOmega )$ is the P1 finite element space, then Assumption 2.2 is realized as $C_\varOmega (h)=\frac{h}{\pi }$, where $h$ is the mesh size (see e.g., [1, 7]).

Let $V_k^1(J)$ be a finite-dimensional subspace of $V^1(J)$ dependent on the discretization parameter $k$. For example, $V_k^1(J)$ is considered to be a finite element space with mesh size (time step size) $k$. Let $m$ be the number of degrees of freedom for $V_k^1(J)$, and let $\{\psi _i\}_{i=1}^m \subset V^1(J)$ be the basis functions of $V_k^1(J)$. Moreover, we denote a vector of the basis functions of $V_k^1(J)$ by $\psi :=(\psi _1,\ldots ,\psi _m)^T$.

We assume that $\varPi _k:V^1(J) \rightarrow V_k^1(J)$ is a Lagrange interpolation operator. Namely, if the mesh points on $J$ are taken as $0=t_0<t_1<\cdots <t_m=T$, for any element $u \in V^1(J)$, $\varPi _ku \in V_k^1(J)$ satisfies

$$\begin{aligned} u(t_i) = \bigl (\varPi _ku\bigr )(t_i), \quad \forall i \in \{1,\ldots ,m\}. \end{aligned}$$

(8)

We need the following assumption as the a priori error estimate for $\varPi _k$.

Assumption 2.3

There exists a positive constant $C_J(k)$ satisfying

$$\begin{aligned} \left\| {u-\varPi _ku}\right\| _{L^2(J)}&\le C_J(k)\left\| {u}\right\| _{V^1(J)}, \quad \forall u\in V^1(J). \end{aligned}$$

(9)

For example, if $V_k^1(J)$ is the P1 finite element space, then Assumption 2.3 is realized by $C_J(k)=\frac{k}{\pi }$ (see e.g., [15, Theorem 2.4]).

Let $V^1\bigl (J;S_h(\varOmega )\bigr )$ and $V_k^1\bigl (J;S_h(\varOmega )\bigr )$ be the semidiscretization and the full-discretization subspaces of $V$, respectively. We now define the semidiscretization operator $P_h:V \rightarrow V^1\bigl (J;S_h(\varOmega )\bigr )$ by the following weak form for any $u \in V$

$$\begin{aligned} \left( {\frac{\partial {}}{\partial {t}}}\bigl (u-P_hu\bigr )(t),v_h\right) _{L^2(\varOmega )} + \nu \left( \nabla \bigl (u-P_hu\bigr )(t),\nabla v_h\right) _{L^2(\varOmega )^d} = 0, \nonumber \\ \forall v_h \in S_h(\varOmega ),~~{\mathrm{a.e.}}~~t \in J. \end{aligned}$$

(10)

Then the full-discretization operator $P_{h,k}:V \rightarrow V_k^1\bigl (J;S_h(\varOmega )\bigr )$ is defined as the composition of $P_h$ and $\varPi _k$, that is, by $P_{h,k}:=\varPi _kP_h$.

3 Constructive a priori error estimates

In this section, we introduce some results for the stability of, and a priori error estimates for, the full-discretization operator $P_{h,k}$. Since the results of this section are given in [11], we omit the proofs.

Theorem 3.1

([11, Lemma 5.3 & Theorem 5.4]) Under Assumption 2.1 and Assumption 2.3, the following constructive a priori estimate holds,

$$\begin{aligned} \left\| {P_{h,k}u}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )}&\le \left( \frac{C_{s,2}}{\nu } +C_{\mathrm{inv}}(h)C_J(k)\right) \left\| {{\frac{\partial {u}}{\partial {t}}}-\nu \triangle u}\right\| _{L^2L^2}, \quad \forall u\in D(\triangle _t). \end{aligned}$$

(11)

Moreover, if $V_k^1(J)$ is the P1 finite element space then we have the following estimates:

$$\begin{aligned} \left\| {P_{h,k}u}\right\| _{V^1\bigl (J;L^2(\varOmega )\bigr )}&\le 2\left\| {{\frac{\partial {u}}{\partial {t}}}-\nu \triangle u}\right\| _{L^2\bigl (J;L^2(\varOmega )\bigr )}, \quad \forall u\in D(\triangle _t). \end{aligned}$$

(12)

Since the full-discretization scheme proposed in [6, 9] has no $V^1L^2$ stability, we can say that the present full-discretized approximation has better properties, in an analytical and practical sense.

Finally, we introduce the constructive a priori error estimates for $P_{h,k}$.

Theorem 3.2

([11, Theorem 5.5 & Theorem 5.6]) Under the assumptions 2.1– 2.3, we have the following constructive a priori error estimates:

$$\begin{aligned} \left\| {u-P_{h,k}u}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )}&\le C_1(h,k)\left\| {{\frac{\partial {u}}{\partial {t}}}-\nu \triangle u}\right\| _{L^2\bigl (J;L^2(\varOmega )\bigr )}, \quad \forall u\in D(\triangle _t),\end{aligned}$$

(13)

$$\begin{aligned} \left\| {u-P_{h,k}u}\right\| _{L^2\bigl (J;L^2(\varOmega )\bigr )}&\le C_0(h,k)\left\| {{\frac{\partial {u}}{\partial {t}}}-\nu \triangle u}\right\| _{L^2\bigl (J;L^2(\varOmega )\bigr )}, \quad \forall u\in D(\triangle _t), \end{aligned}$$

(14)

where $C_1(h,k):=\frac{2}{\nu }C_\varOmega (h) + C_{\mathrm{inv}}(h)C_J(k)$ and $C_0(h,k)=\frac{8}{\nu }C_\varOmega (h)^2+C_J(k)$.

4 Discretized quasi-Newton scheme

In this section, we consider a full-discretized approximation scheme for solutions of (1) by using a quasi-Newton operator. Since the full-discretization scheme in this paper uses interpolation in time, its computational method is somewhat complicated. However, it enables us to get an efficient and accurate estimation of the inverse operator norm in (2), as well as the verified computation of solutions to nonlinear problems.

We first describe an easy, but an important operation of matrix-vector multiplication.

Definition 4.1

Let $M$ be an $m_1$-by-$m_2$ matrix. Then, we define the $m_1m_2$ vector $\mathrm{vec}\left( M\right)$ as follows:

$$\begin{aligned} \mathrm{vec}\left( M\right) := \left( M_{1,1}, M_{1,2}, \ldots , M_{1,m_2}, M_{2,1}, \ldots , M_{m_1,m_2} \right) ^T. \end{aligned}$$

(15)

We call this transformation a “row-major matrix-vector transformation”.

Definition 4.2

Let $M$ be an $m_1$-by-$m_2$ matrix. Then, we define the block diagonal matrix $\left( I_{n}\otimes {M}\right)$ as follows:

$$\begin{aligned} \left( I_{n}\otimes {M}\right) := \underbrace{ \begin{pmatrix} M &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} M \end{pmatrix}}_{n}. \end{aligned}$$

(16)

Here, $I_n$ is the $n$-by-$n$ identity matrix, and the operator $\otimes$ denotes the Kronecker product.

From these definitions, we have the following lemma.

Lemma 4.3

For an arbitrary $n$-by-$m$ matrix $M$ and $m$-dimensional vector $x$, the following equality holds:

$$\begin{aligned} Mx = \left( I_{n}\otimes {x^T}\right) \mathrm{vec}\left( M\right) . \end{aligned}$$

(17)

Proof

The elements of $Mx$ are calculated by

$$\begin{aligned} Mx = \begin{pmatrix} M_{1,1} &{} \cdots &{} M_{1,m} \\ \vdots &{} \ddots &{} \vdots \\ M_{n,1} &{} \cdots &{} M_{n,m} \end{pmatrix} \begin{pmatrix} x_1 \\ \vdots \\ x_m \end{pmatrix} = \begin{pmatrix} M_{1,1}x_1 + \cdots + M_{1,m}x_m \\ \vdots \\ M_{n,1}x_1 + \cdots + M_{n,m}x_m \end{pmatrix}. \end{aligned}$$

On the other hand, the elements of $\left( I_{n}\otimes {x^T}\right) \mathrm{vec}\left( M\right)$ are calculated by

$$\begin{aligned} \left( I_{n}\otimes {x^T}\right) \mathrm{vec}\left( M\right)&= \begin{pmatrix} x^T &{} \cdots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} x^T \end{pmatrix} \begin{pmatrix} M_{1,1} \\ \vdots \\ M_{n,m} \end{pmatrix} = \begin{pmatrix} M_{1,1}x_1 + \cdots + M_{1,m}x_m \\ \vdots \\ M_{n,1}x_1 + \cdots + M_{n,m}x_m \end{pmatrix}. \end{aligned}$$

Therefore, the corresponding components coincide with each other.$\square$

Next, we consider the quasi-Newton operator of (1) and its full-discretization. Let $A$ be an integral operator defined by $A:=-I_e\triangle _t^{-1}(b\cdot \nabla +c):L^2\bigl (J;H_0^1(\varOmega )\bigr ) \rightarrow L^2\bigl (J;H_0^1(\varOmega )\bigr )$. Since the domain of $\triangle _t$ is $D(\triangle _t)$, denoting the range of $A$ by $R(A)$, it holds that $R(A) \subset D(\triangle _t)=V^1L^2 \cap L^2D(\triangle )$. Then, the differential operator of the left-hand side of (1a) can be represented as $\fancyscript{L}_t=\triangle _t(I-A)$, where $I$ denotes the identity operator on $D(\triangle _t)$. We define the quasi-Newton operator as the inverse of $I-A$, i.e., $(I-A)^{-1}:L^2H_0^1 \rightarrow L^2H_0^1$.

We now define the symmetric and positive definite matrices $L_\phi$ and $D_\phi \in \mathbb R ^{n \times n}$ by

$$\begin{aligned} L_{\phi ,i,j}:=\left( \phi _j,\phi _i\right) _{L^2(\varOmega )}, \quad D_{\phi ,i,j}:=\left( \nabla \phi _j,\nabla \phi _i\right) _{L^2(\varOmega )^d}, \quad \forall i,j \in \{1,\ldots ,n\}. \end{aligned}$$

Let $L_\phi ^{1/2}$ and $D_\phi ^{1/2}$ be the Cholesky factors of $L_\phi$ and $D_\phi$, respectively, i.e., the following equalities hold

$$\begin{aligned} L_\phi =L_\phi ^{1/2}L_\phi ^{T/2}, \quad D_\phi =D_\phi ^{1/2}D_\phi ^{T/2}, \end{aligned}$$

where $L_\phi ^{1/2}$ and $D_\phi ^{1/2}$ are lower triangular matrices, and $L_\phi ^{T/2}$ and $D_\phi ^{T/2}$ are those matrices transposed. Let $L_\psi \in \mathbb R ^{m \times m}$ be the symmetric and positive-definite matrix whose elements are defined by $L_{\psi ,i,j}:=\left( \psi _j,\psi _i\right) _{L^2(J)}$. We define $Z_\phi \in L^\infty (J)^{n \times n}$ as the matrix function on $J$ whose elements are defined by

$$\begin{aligned} Z_{\phi ,i,j}:=\left( (b\cdot \nabla )\phi _j +c\phi _j,\phi _i\right) _{L^2(\varOmega )}, \quad \forall i,j \in \{1,\ldots ,n\}. \end{aligned}$$

For any $i \in \{1, \ldots , m\}$, we define the matrices $\tilde{G}_{\phi ,\psi }^{(i)} \in \mathbb R ^{n \times nm}$ and $\tilde{G}_{\phi ,\psi } \in \mathbb R ^{nm \times nm}$ by

$$\begin{aligned} \tilde{G}_{\phi ,\psi }^{(i)} :=\int \limits _0^{t_i}\exp \left( (s-t_i)\nu L_\phi ^{-1}D_\phi \right) L_\phi ^{-1}Z_\phi (s)\left( I_{n}\otimes {\psi (s)^T}\right) \,ds, \quad \tilde{G}_{\phi ,\psi } :=\begin{pmatrix} \tilde{G}_{\phi ,\psi }^{(1)} \\ \vdots \\ \tilde{G}_{\phi ,\psi }^{(m)} \end{pmatrix}. \end{aligned}$$

(18)

Moreover, we define $G_{\phi ,\psi } \in \mathbb R ^{nm \times nm}$ as $G_{\phi ,\psi }:=I_{nm}-\tilde{G}_{\phi ,\psi }$.

We obtain the Theorem 4.4 as a full-discretization scheme of the quasi-Newton operator.

Theorem 4.4

Let $V_k^1(J)$ be a finite element space constituted by the Lagrange elements. For a function $f_{h,k} \in V_k^1\bigl (J;S_h(\varOmega )\bigr )$, let $u_{h,k} \in V_k^1\bigl (J;S_h(\varOmega )\bigr )$ be a solution of the following equation

$$\begin{aligned} u_{h,k} - P_{h,k}Au_{h,k} = f_{h,k}. \end{aligned}$$

(19)

Then, the unique existence of a solution $u_{h,k}$ of (19) is equivalent to the nonsingularity of $G_{\phi ,\psi }$.

Proof

First, we consider $P_{h,k}Au_{h,k}$. For an arbitrary $u_{h,k} \in V_k^1\bigl (J;S_k(\varOmega )\bigr )$, there exists a matrix $U \in \mathbb R ^{n \times m}$ such that $u_{h,k}(x,t)=\phi (x)^TU\psi (t)$. Let $w_h:=P_hAu_{h,k}$. Similarly, from $w_h \in V^1\bigl (J;S_h(\varOmega )\bigr )$, there exists a vector function $\mathfrak w \in V^1(J)^n$ such that

$$\begin{aligned} w_h(x,t)=\phi (x)^T\mathfrak w (t)=\sum _{i=1}^n \phi _i(x)\mathfrak w _i(t). \end{aligned}$$

For each $v_h \in S_h(\varOmega )$, and almost everywhere $t \in J$, from the definition of $P_h$ and the operator $A$, we have

$$\begin{aligned}&\left( {\frac{\partial {w_h}}{\partial {t}}}(t),v_h\right) _{L^2(\varOmega )} + \nu \left( \nabla w_h(t),\nabla v_h\right) _{L^2(\varOmega )^d} \nonumber \\&\qquad = \left( {\frac{\partial {Au_{h,k}}}{\partial {t}}}(t),v_h\right) _{L^2(\varOmega )} + \nu \left( \nabla Au_{h,k}(t),\nabla v_h\right) _{L^2(\varOmega )^d}, \nonumber \\&\qquad = \left( \bigl (b(t)\cdot \nabla \bigr )u_{h,k}(t) +c(t)u_{h,k}(t),v_h\right) _{L^2(\varOmega )}. \end{aligned}$$

(20)

From the arbitrariness of $v_h \in S_h(\varOmega )$, the variational equation (20) is equivalent to the following system of first-order linear ODEs with homogeneous initial conditions

$$\begin{aligned} \left( L_\phi \frac{d}{dt}+\nu D_\phi \right) \mathfrak w = Z_\phi U\psi . \end{aligned}$$

(21)

Since (21) is an initial-value problem for an ODE system with constant coefficients, by using its fundamental matrix, $\mathfrak w$ can be presented as

$$\begin{aligned} \mathfrak w (t)&= \int \limits _0^t\exp \left( (s-t)\nu L_\phi ^{-1}D_\phi \right) L_\phi ^{-1}Z_\phi (s)U\psi (s)\,ds \end{aligned}$$

(22)

$$\begin{aligned}&= \left( \int \limits _0^t\exp \left( (s-t)\nu L_\phi ^{-1}D_\phi \right) L_\phi ^{-1}Z_\phi (s) \left( I_{n}\otimes {\psi (s)^T}\right) \,ds\right) \mathrm{vec}\left( U\right) , \end{aligned}$$

(23)

where we have used (17) to make the deformation from (22) to (23). And, from (18), we have

$$\begin{aligned} \mathfrak w (t_i) = \tilde{G}_{\phi ,\psi }^{(i)}\mathrm{vec}\left( U\right) \in \mathbb R ^n, \quad \forall i \in \{1, \ldots , m\}. \end{aligned}$$

(24)

Thus, from (23), we obtain the following relation between $U$ and $\mathfrak w$:

$$\begin{aligned} \left( \mathfrak w (t_1)^T,\ldots , \mathfrak w (t_m)^T\right) ^T=\tilde{G}_{\phi ,\psi }\mathrm{vec}\left( U\right) . \end{aligned}$$

Now, we prove that if (19) is solvable for each $f_{h,k} \in V_k^1\bigl (J;S_h(\varOmega )\bigr )$, then $G_{\phi ,\psi }$ is nonsingular. For an $f_{h,k} \in V_k^1\bigl (J;S_h(\varOmega )\bigr )$, we denote the solution of (19) as $u_{h,k} \in V_k^1\bigl (J;S_h(\varOmega )\bigr )$. From the fact that $f_{h,k} \in V_k^1S_h$, there exists an $F\in \mathbb R ^{n \times m}$ such that $f_{h,k}(x,t)=\phi (x)^TF\psi (t)$. Note that, for any nodal points $t_i$, we have $(P_{h,k}Au_{h,k})(x,t_i)=(\varPi _kw_h)(x,t_i)=\phi (x)^T\mathfrak w (t_i)$ by the definition of $\varPi _k$. Therefore, from (19) and (24), we have

$$\begin{aligned} u_{h,k}(x,t_i)-f_{h,k}(x,t_i)&= (P_{h,k}Au_{h,k})(x,t_i), \quad \forall x \in \varOmega ,~\forall i \in \{1, \ldots , m\}, \\&= (\varPi _kw_h)(x,t_i), \end{aligned}$$

which implies

$$\begin{aligned} \phi (x)^T(U-F)\psi (t_i)&= \phi (x)^T\mathfrak w (t_i) \nonumber \\&= \phi (x)^T\tilde{G}_{\phi ,\psi }^{(i)}\mathrm{vec}\left( U\right) . \end{aligned}$$

(25)

Since we assume that $V_k^1(J)$ is the finite element space constituted by the Lagrange elements, $\psi _j(t_i)=\delta _{j,i}$ is satisfied, where $\delta _{j,i}$ denotes the Kronecker delta. Therefore, we get

$$\begin{aligned} (U-F)\psi (t_i) = \begin{pmatrix} U_{1,1}-F_{1,1} &{} \cdots &{} U_{1,m}-F_{1,m} \\ \vdots &{} \ddots &{} \vdots \\ U_{n,1}-F_{n,1} &{} \cdots &{} U_{n,m}-F_{n,m} \end{pmatrix} \begin{pmatrix} \psi _1(t_i) \\ \vdots \\ \psi _m(t_i) \end{pmatrix} = \begin{pmatrix} U_{1,i}-F_{1,i} \\ \vdots \\ U_{n,i}-F_{n,i} \end{pmatrix}. \end{aligned}$$

From the arbitrariness of $x$ and $i$, the variational equation (25) is equivalent to the following simultaneous linear equations:

$$\begin{aligned} \mathrm{vec}\left( U-F\right)&= \tilde{G}_{\phi ,\psi }\mathrm{vec}\left( U\right) . \end{aligned}$$

Namely, we have

$$\begin{aligned} \left( I_{nm}-\tilde{G}_{\phi ,\psi }\right) \mathrm{vec}\left( U\right)&= \mathrm{vec}\left( F\right) . \end{aligned}$$

Therefore, from the arbitrariness of $f_{h,k}$, the nonsingularity of $I_{nm}-\tilde{G}_{\phi ,\psi }$ follows.

The converse of this proposition is easily obtained by reversing the discussion. $\square$

When we apply the proposed a posteriori estimates, it is necessary to confirm that $G_{\phi ,\psi }$ is nonsingular, which will be able to verify by validated computations such as [14]. Therefore, in what follows, we always assume the nonsingularity of $G_{\phi ,\psi }$. Moreover, we define the linear operator $[I-A]_{h,k}^{-1}:V_k^1\bigl (J;S_h(\varOmega )\bigr ) \rightarrow V_k^1\bigl (J;S_h(\varOmega )\bigr )$ by the solution of (19). We call this operator a “fully discretized quasi-Newton operator”.

5 A posteriori estimates

In this section, we derive a new a posteriori estimate to obtain $C_{L^2L^2,L^2H_0^1}$, which satisfies (2) by using the fully discretized quasi-Newton operator.

First, we describe a method to calculate the norm of the elements in the full-discretization space. Let $K_{\phi ,\psi }$ be a matrix in $\mathbb R ^{nm \times nm}$ defined by

$$\begin{aligned} K_{\phi ,\psi } := D_\phi \otimes L_\psi = \begin{pmatrix} D_{\phi ,1,1}L_\psi &{} \cdots &{} D_{\phi ,1,n}L_\psi \\ \vdots &{} \ddots &{} \vdots \\ D_{\phi ,n,1}L_\psi &{} \cdots &{} D_{\phi ,n,n}L_\psi \end{pmatrix}. \end{aligned}$$

(26)

From the symmetric positive definiteness of $D_\phi$ and $L_\psi$, it is readily seen that $K_{\phi ,\psi }$ is also symmetric positive definite. Therefore, $K_{\phi ,\psi }$ is Cholesky decomposable such that $K_{\phi ,\psi }=K_{\phi ,\psi }^{1/2}K_{\phi ,\psi }^{T/2}$. Similarly, we define the matrix $L_{\phi ,\psi }$ in $\mathbb R ^{nm \times nm}$ as $L_{\phi ,\psi } := L_\phi \otimes L_\psi$.

Lemma 5.1

For an element $u_{h,k} \in V_k^1\bigl (J;S_h(\varOmega )\bigr )$, taking $U\in \mathbb R ^{n \times m}$ such that $u_{h,k}=\phi ^TU\psi$, then the following equalities hold

$$\begin{aligned} \left\| {u_{h,k}}\right\| _{L^2\bigl (J;L^2(\varOmega )\bigr )}&= \left| L_{\phi ,\psi }^{T/2}\mathrm{vec}\left( U\right) \right| , \end{aligned}$$

(27)

$$\begin{aligned} \left\| {u_{h,k}}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )}&= \left| K_{\phi ,\psi }^{T/2}\mathrm{vec}\left( U\right) \right| , \end{aligned}$$

(28)

where $\left| ~\cdot ~\right|$ denotes the Euclidean norm of a vector.

Proof

Since the proofs of (27) and (28) are almost the same, we will prove only (27). From (17), we have

$$\begin{aligned} \left\| {u_{h,k}}\right\| _{L^2\bigl (J;L^2(\varOmega )\bigr )}^2&= \int \limits _J\int \limits _\varOmega \psi (t)^TU^T\phi (x)\phi (x)^TU\psi (t)\,dxdt \\&\!=\! \int \limits _J\int \limits _\varOmega \mathrm{vec}\left( U\right) ^T\left( I_{n}\otimes {\psi (t)}\right) ^T\phi (x)\phi (x)^T\left( I_{n}\otimes {\psi (t)^T}\right) \mathrm{vec}\left( U\right) \,dxdt\\&= \mathrm{vec}\left( U\right) ^T \int \limits _J \left( I_{n}\otimes {\psi (t)}\right) ^TL_\phi \left( I_{n}\otimes {\psi (t)^T}\right) \,dt\,\mathrm{vec}\left( U\right) \\&= \mathrm{vec}\left( U\right) ^T \int \limits _J \begin{pmatrix} L_{\phi ,1,1}\psi (t)\psi (t)^T &{} \cdots &{} L_{\phi ,1,n}\psi (t)\psi (t)^T\\ \vdots &{} \ddots &{} \vdots \\ L_{\phi ,n,1}\psi (t)\psi (t)^T &{} \cdots &{} L_{\phi ,n,n}\psi (t)\psi (t)^T \end{pmatrix}\,dt\,\mathrm{vec}\left( U\right) \\&= \mathrm{vec}\left( U\right) ^T \begin{pmatrix} L_{\phi ,1,1}L_\psi &{} \cdots &{} L_{\phi ,1,n}L_\psi \\ \vdots &{} \ddots &{} \vdots \\ L_{\phi ,n,1}L_\psi &{} \cdots &{} L_{\phi ,n,n}L_\psi \end{pmatrix}\mathrm{vec}\left( U\right) \\&= \left( L_{\phi ,\psi }^{T/2}\mathrm{vec}\left( U\right) \right) ^T\left( L_{\phi ,\psi }^{T/2}\mathrm{vec}\left( U\right) \right) , \end{aligned}$$

which proves equation (27). $\square$

Let $M_{\phi ,\psi }(h,k)$ be a nonnegative constant defined by $M_{\phi ,\psi }(h,k):=\left\| {K_{\phi ,\psi }^{T/2}G_{\phi ,\psi }^{-1}K_{\phi ,\psi }^{-T/2}}\right\| _{2}$, where $\left\| {~\cdot ~}\right\| _{2}$ denotes the matrix two-norm. The following theorem for $M_{\phi ,\psi }$ holds.

Theorem 5.2

It holds that

$$\begin{aligned} \left\| {[I-A]_{h,k}^{-1}f_{h,k}}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )} \le M_{\phi ,\psi }\left\| {f_{h,k}}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )}, \quad \forall f_{h,k} \in V_k^1S_h. \end{aligned}$$

(29)

Proof

For any $f_{h,k} \in V_k^1S_h$, we set $u_{h,k}:=[I-A]_{h,k}^{-1}f_{h,k} \in V_k^1S_h$. Since $f_{h,k}$ and $u_{h,k}$ are the elements of $V_k^1\bigl (J;S_h(\varOmega )\bigr )$, there exist matrices $F$ and $U$ in $\mathbb R ^{n \times m}$ such that $f_{h,k}=\phi ^TF\psi$ and $u_{h,k}=\phi ^TU\psi$, respectively. Moreover, from the proof of Theorem 4.4, it follows that $\mathrm{vec}\left( U\right) =G_{\phi ,\psi }^{-1}\mathrm{vec}\left( F\right)$. Therefore, we have the following estimates

$$\begin{aligned} \left\| {u_{h,k}}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )}^2&= \mathrm{vec}\left( U\right) ^TK_{\phi ,\psi }\mathrm{vec}\left( U\right) \\&= \left( K_{\phi ,\psi }^{T/2}\mathrm{vec}\left( U\right) \right) ^T\left( K_{\phi ,\psi }^{T/2}G_{\phi ,\psi }^{-1} K_{\phi ,\psi }^{-T/2}\right) \left( K_{\phi ,\psi }^{T/2}\mathrm{vec}\left( F\right) \right) \\&\le \left\| {u_{h,k}}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )} \left\| {K_{\phi ,\psi }^{T/2}G_{\phi ,\psi }^{-1}K_{\phi ,\psi }^{-T/2}}\right\| _{2}\left\| {f_{h,k}}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )}. \end{aligned}$$

This completes the proof.$\square$

Let $\fancyscript{C}_0$ and $\fancyscript{C}_1$ be the nonnegative constants defined by

$$\begin{aligned} \fancyscript{C}_0&:= M_{\phi ,\psi }\left( \frac{C_{s,2}}{\nu }+C_{\mathrm{inv}}(h)C_J(k)\right) ,&\fancyscript{C}_1&:= \left\| {b}\right\| _{L^\infty L^\infty }+C_{s,2}\left\| {c}\right\| _{L^\infty L^\infty }, \end{aligned}$$

respectively. Moreover, we define the constant $\kappa _{\phi ,\psi }$ as follows:

$$\begin{aligned} \kappa _{\phi ,\psi }&:= \frac{\left\| {b}\right\| _{L^\infty L^\infty }(1+\fancyscript{C}_0\fancyscript{C}_1)C_1(h,k) +\fancyscript{C}_0\fancyscript{C}_1C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }}{1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }}, \end{aligned}$$

(30)

provided that $1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }\not =0$.

Theorem 5.3

Assume that

$$\begin{aligned} 0 \le \kappa _{\phi ,\psi } < 1. \end{aligned}$$

(31)

Then under the same assumptions as in Theorem 3.2, we have the following constructive a posteriori estimates

$$\begin{aligned} \left\| {\fancyscript{L}_t^{-1}}\right\| _{\fancyscript{L}\bigl (L^2(J;L^2(\varOmega )),L^2(J;H_0^1(\varOmega ))\bigr )}&\le \frac{1}{1-\kappa _{\phi ,\psi }} \frac{\fancyscript{C}_0+(1+\fancyscript{C}_0 \fancyscript{C}_1)C_1(h,k)}{1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }}. \end{aligned}$$

(32)

Proof

For any $f \in L^2\bigl (J;L^2(\varOmega )\bigr )$, we set $u:=\fancyscript{L}_t^{-1}f \in D(\triangle _t)$. Then we make the following decomposition of (1) into two parts, e.g., the finite- and infinite-dimensional parts, using the projection $P_{h,k}$. Namely, in the space $L^2\bigl (J;H_0^1(\varOmega )\bigr )$, using the following equivalency

$$\begin{aligned} {\frac{\partial {u}}{\partial {t}}}&- \nu \triangle u + (b\cdot \nabla )u + cu = f \nonumber \\&\Longleftrightarrow u = I_e\triangle _t^{-1}\bigl (-(b\cdot \nabla )u-cu+f\bigr ), \end{aligned}$$

(33)

we have the decomposition:

We set $u_\perp :=u-P_{h,k}u$ for short. From (34a), using the definition of the operator $A$, we have

$$\begin{aligned} P_{h,k}u = P_{h,k}\left( A(P_{h,k}u+u_{\perp })+I_{e}{\triangle }_{t}^{-1}f\right) , \end{aligned}$$

by the definition of the operator $[I-A]_{h,k}^{-1}$, which implies

$$\begin{aligned} P_{h,k}u = [I-A]_{h,k}^{-1}P_{h,k}\bigl (Au_\perp +I_e\triangle _t^{-1}f\bigr ). \end{aligned}$$

Therefore, from (29) and (11), we have the following estimates,

$$\begin{aligned} \left\| {P_{h,k}u}\right\| _{L^2H_0^1}&\le M_{\phi ,\psi }\left( \left\| {P_{h,k}Au_\perp }\right\| _{L^2H_0^1} + \left\| {P_{h,k}I_e\triangle _t^{-1}f}\right\| _{L^2H_0^1}\right) \\&\le M_{\phi ,\psi }\left( \frac{C_{s,2}}{\nu } +C_{\mathrm{inv}}(h)C_J(k)\right) \left( \left\| {(b\cdot \nabla +c)u_\perp }\right\| _{L^2L^2} + \left\| {f}\right\| _{L^2L^2}\right) . \end{aligned}$$

From the definition of $\fancyscript{C}_0$, we have

$$\begin{aligned} \left\| {P_{h,k}u}\right\| _{L^2H_0^1}&\le \fancyscript{C}_0\left\| {(b\cdot \nabla ) u_\perp +cu_\perp }\right\| _{L^2L^2}+\fancyscript{C}_0\left\| {f}\right\| _{L^2L^2} \nonumber \\&\le \fancyscript{C}_0\left\| {b}\right\| _{L^\infty L^\infty } \left\| {u_\perp }\right\| _{L^2H_0^1}+\fancyscript{C}_0\left\| {c}\right\| _{L^\infty L^\infty }\left\| {u_\perp }\right\| _{L^2L^2} + \fancyscript{C}_0\left\| {f}\right\| _{L^2 L^2}. \end{aligned}$$

(35)

By calculating the $L^2L^2$ norm of (34b) using (14), we have

$$\begin{aligned} \left\| {u_\perp }\right\| _{L^2L^2}&\le C_0(h,k)\left\| {-(b\cdot \nabla )u-cu+f}\right\| _{L^2L^2} \\&\le C_0(h,k)\bigl ( \left\| {b}\right\| _{L^\infty L^\infty }\left\| {u}\right\| _{L^2H_0^1}+\left\| {c}\right\| _{L^\infty L^\infty }\left\| {u}\right\| _{L^2L^2}+\left\| {f}\right\| _{L^2L^2}\bigr ), \end{aligned}$$

which yields

$$\begin{aligned}&\bigl (1\!-\!C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }\bigr )\left\| {u_\perp }\right\| _{L^2L^2} \le C_0(h,k)\bigl ( \left\| {b}\right\| _{L^\infty L^\infty }\left\| {u}\right\| _{L^2H_0^1}\\&\quad +\left\| {c}\right\| _{L^\infty L^\infty }\left\| {P_{h,k}u}\right\| _{L^2L^2}\!+\!\left\| {f}\right\| _{L^2L^2}\bigr ). \end{aligned}$$

From (31), $1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty } >0$ is satisfied. Therefore, we obtain

$$\begin{aligned} \left\| {u_\perp }\right\| _{L^2L^2}&\le \frac{C_0(h,k)}{1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }}\Bigl (\left\| {b}\right\| _{L^\infty L^\infty } \left\| {P_{h,k}u+u_\perp }\right\| _{L^2H_0^1} \nonumber \\&\quad +C_{s,2}\left\| {c}\right\| _{L^\infty L^\infty } \left\| {P_{h,k}u}\right\| _{L^2H_0^1}+\left\| {f}\right\| _{L^2L^2}\Bigr ) \nonumber \\&\le \frac{C_0(h,k)}{1-C_0(h,k) \left\| {c}\right\| _{L^\infty L^\infty }}\bigl (\fancyscript{C}_1 \left\| {P_{h,k}u}\right\| _{L^2H_0^1}+\left\| {b}\right\| _{L^\infty L^\infty } \left\| {u_\perp }\right\| _{L^2H_0^1}+\left\| {f}\right\| _{L^2L^2}\bigr ). \end{aligned}$$

(36)

Thus (35) is estimated as

$$\begin{aligned} \left\| {P_{h,k}u}\right\| _{L^2H_0^1}&\le \fancyscript{C}_0\left\| {b}\right\| _{L^\infty L^\infty } \left\| {u_\perp }\right\| _{L^2H_0^1} + \fancyscript{C}_0\left\| {f}\right\| _{L^2 L^2} \nonumber \\&\quad +\fancyscript{C}_0\frac{C_0(h,k) \left\| {c}\right\| _{L^\infty L^\infty }}{1-C_0(h,k) \left\| {c}\right\| _{L^\infty L^\infty }}\Bigl (\fancyscript{C}_1 \left\| {P_{h,k}u}\right\| _{L^2H_0^1}\nonumber \\&\quad +\left\| {b}\right\| _{L^\infty L^\infty } \left\| {u_\perp }\right\| _{L^2H_0^1}+\left\| {f}\right\| _{L^2L^2}\Bigr ). \end{aligned}$$

(37)

Setting nonnegative constants $R_{1,1}$, $R_{1,2}$, and $b_1$ as follows:

$$\begin{aligned} R_{1,1}&:= 1-\fancyscript{C}_0\fancyscript{C}_1\frac{C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }}{1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }},&R_{1,2}&:= \frac{\fancyscript{C}_0\left\| {b}\right\| _{L^\infty L^\infty }}{1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }}, \\ b_1&:= \frac{\fancyscript{C}_0}{1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }},&\end{aligned}$$

(37) is rewritten as

$$\begin{aligned} R_{1,1}\left\| {P_{h,k}u}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )} - R_{1,2}\left\| {u_\perp }\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )}&\le b_1\left\| {f}\right\| _{L^2\bigl (J;L^2(\varOmega )\bigr )}. \end{aligned}$$

(38)

On the other hand, by considering the $L^2H_0^1$ norm of (34b), from (13) we have

$$\begin{aligned} \left\| {u_\perp }\right\| _{L^2H_0^1}&\le C_1(h,k)\left\| {-(b\cdot \nabla )u-cu+f}\right\| _{L^2L^2} \\&\le C_1(h,k)\left( \left\| {b}\right\| _{L^\infty L^\infty }\left\| {P_{h,k}u+u_\perp }\right\| _{L^2H_0^1}\right. \\&\quad \left. +\left\| {c}\right\| _{L^\infty L^\infty }\left\| {P_{h,k}u+u_\perp }\right\| _{L^2L^2}+\left\| {f}\right\| _{L^2L^2}\right) \\&\le C_1(h,k)\left( \fancyscript{C}_1\left\| {P_{h,k}u}\right\| _{L^2H_0^1}+\left\| {b}\right\| _{L^\infty L^\infty }\left\| {u_\perp }\right\| _{L^2H_0^1}\right. \\&\quad \left. +\left\| {c}\right\| _{L^\infty L^\infty }\left\| {u_\perp }\right\| _{L^2L^2}+\left\| {f}\right\| _{L^2L^2}\right) . \end{aligned}$$

From (36), we obtain

$$\begin{aligned} \left\| {u_\perp }\right\| _{L^2H_0^1}&\le C_1(h,k)\fancyscript{C}_1\left\| {P_{h,k}u}\right\| _{L^2H_0^1}\nonumber \\&\quad +C_1(h,k)\left\| {b}\right\| _{L^\infty L^\infty }\left\| {u_\perp }\right\| _{L^2H_0^1}+C_1(h,k)\left\| {f}\right\| _{L^2L^2} \nonumber \\&\quad +C_1(h,k)\frac{C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }}{1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }}\bigl (\fancyscript{C}_1\left\| {P_{h,k}u}\right\| _{L^2H_0^1}\nonumber \\&\quad +\left\| {b}\right\| _{L^\infty L^\infty }\left\| {u_\perp }\right\| _{L^2H_0^1}+\left\| {f}\right\| _{L^2L^2}\bigr ). \end{aligned}$$

(39)

We set nonnegative constants $R_{2,1}$, $R_{2,2}$, and $b_2$ as follows:

$$\begin{aligned} R_{2,1}&:= \frac{\fancyscript{C}_1C_1(h,k)}{1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }},&R_{2,2}&:= 1-\frac{\left\| {b}\right\| _{L^\infty L^\infty }C_1(h,k)}{1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }}, \\ b_2&:= \frac{C_1(h,k)}{1-C_0(h,k)\left\| {c}\right\| _{L^\infty L^\infty }},&\end{aligned}$$

where we note that the positivity of $R_{2,2}$ follows by the condition (31). Thus (39) can be rewritten as

$$\begin{aligned} -R_{2,1}\left\| {P_{h,k}u}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )} + R_{2,2}\left\| {u_\perp }\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )}&\le b_2\left\| {f}\right\| _{L^2\bigl (J;L^2(\varOmega )\bigr )}. \end{aligned}$$

(40)

From (38) and (40), we have the following simultaneous inequalities,

$$\begin{aligned} \begin{pmatrix} R_{1,1} &{} -R_{1,2} \\ -R_{2,1} &{} R_{2,2} \end{pmatrix} \begin{pmatrix} \left\| {P_{h,k}u}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )} \\ \left\| {u_\perp }\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )} \end{pmatrix} \le \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}\left\| {f}\right\| _{L^2\bigl (J;L^2(\varOmega )\bigr )}. \end{aligned}$$

By assumption (31), we obtain

$$\begin{aligned} \det \begin{pmatrix} R_{1,1} &{} -R_{1,2} \\ -R_{2,1} &{} R_{2,2} \end{pmatrix} = 1 - \kappa _{\phi ,\psi } > 0. \end{aligned}$$

Therefore, the simultaneous inequalities can be solved as follows:

$$\begin{aligned} \begin{pmatrix} \left\| {P_{h,k}u}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )} \\ \left\| {u_\perp }\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )} \end{pmatrix}&\le \frac{1}{1-\kappa _{\phi ,\psi }} \begin{pmatrix} R_{2,2} &{} R_{1,2} \\ R_{2,1} &{} R_{1,1} \end{pmatrix} \begin{pmatrix} b_1 \\ b_2 \end{pmatrix}\left\| {f}\right\| _{L^2\bigl (J;L^2(\varOmega )\bigr )}. \end{aligned}$$

(41)

Finally, from (41), we have

$$\begin{aligned} \left\| {u}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )}&\le \left\| {P_{h,k}u}\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )} + \left\| {u_\perp }\right\| _{L^2\bigl (J;H_0^1(\varOmega )\bigr )} \\&\le \frac{R_{2,2}b_1+R_{1,2}b_2+R_{2,1}b_1 +R_{1,1}b_2}{1-\kappa _{\phi ,\psi }}\left\| {f}\right\| _{L^2\bigl (J;L^2(\varOmega )\bigr )}, \end{aligned}$$

which proves the desired estimates.$\square$

6 Numerical examples

In this section, we show several rigorous numerical results for $C_{L^2L^2,L^2H_0^1}$ satisfying (2) for test problems by three kinds of methods, namely, a priori estimates (the Gronwall inequality), a posteriori estimates proposed in [10], and the new method in Theorem 5.3. Moreover, we also show several rigorous error bounds of the numerical solutions for the nonlinear parabolic equations as an application of the estimates of (2).

We considered the norm estimates for an inverse operator of the following $\fancyscript{L}_t$:

$$\begin{aligned} \fancyscript{L}_t:=\frac{\partial }{\partial t}-\nu \triangle -2u_h^k, \end{aligned}$$

(42)

that is, $b=0$ and $c=-2u_h^k$ in (2). Here, $u_h^k$ is assumed to be an approximate solution of the following nonlinear parabolic problem:

Therefore, (42) becomes a linearized operator of (43) at $u_h^k$. We only considered one-space-dimensional case ($d=1$) with $\varOmega =(0,1)$. Furthermore, the function $f$ was chosen so that the problem (43) had the following exact solutions:

• $u(x,t)=0.5 t \sin (\pi x),\, \nu =0.1,$ (Example 1.1);

• $u(x,t)=0.5 t \sin (\pi x),\, \nu =1.0,$ (Example 1.2);

• $u(x,t)=\sin (\pi t)\sin (\pi x),\, \nu =0.1,$ (Example 2.1);

• $u(x,t)=\sin (\pi t)\sin (\pi x),\, \nu =1.0,$ (Example 2.2).

Note that Example 1.1 and Example 2.1 are studied in [10]. In each example, the function $u_h^k$ was computed as an approximation of the corresponding $u$ by using a piecewise-cubic Hermite interpolation in the space direction with a piecewise-linear interpolation in the time direction. Therefore, $u_h^k$ belongs to $V^1\bigl (J;H_0^1(\varOmega ) \cap H^2(\varOmega )\bigr )$.

We used the finite-dimensional spaces $S_h(\varOmega )$ and $V_k^1(J)$, spanned by piecewise linear functions with uniform mesh size $h$ and $k$, respectively, so that they satisfied $k=h^2$. Then, it was seen that the constants in previous sections could be taken as $C_\varOmega (h)=h/\pi$, $C_{\mathrm{inv}}(h)=\sqrt{12}/h$, $C_J(k)=k/\pi =h^2/\pi$, and $C_{s,2}=1/\pi$, respectively. Moreover, we had

$$\begin{aligned} \left\| {c}\right\| _{L^\infty \bigl (J;L^\infty (\varOmega )\bigr )} =2\left\| {u_h^k}\right\| _{L^\infty \bigl (J;L^\infty (\varOmega )\bigr )} \le {\left\{ \begin{array}{ll} T&{}\text {(Example 1.1 and 1.2)}\\ 2&{}\text {(Example 2.1 and 2.2)}. \end{array}\right. } \end{aligned}$$

6.1 A posteriori estimates of the inverse parabolic operator

We now present the results computed for $C_{L^2L^2,L^2H_0^1}$ by using three kinds of method. Here, we used the following a priori estimate, which comes from the Gronwall inequality

$$\begin{aligned} \left\| {\fancyscript{L}_t^{-1}}\right\| _{\fancyscript{L}\bigl (L^2(J;L^2(\varOmega )), L^2(J;H_0^1(\varOmega ))\bigr )}\le \exp ({\gamma T})\frac{C_{s,2}}{\nu },\quad \gamma := \max \left\{ \sup _{\varOmega \times J}(-c), 0\right\} . \end{aligned}$$

In this subsection, we will refer to the a posteriori estimates studied in [10] and our present estimates (32) as “a posteriori estimate I” and “a posteriori estimate II,” respectively. To compute a posteriori estimate I, we used the same parameters as in [10], i.e., $(n, m)=(5, 700 \cdot T^2)$ for Example 1.1, $(n, m)=(5, 100\cdot 4^T)$ for Example 2.1, where we note that $h=1/(n+1)$ and $k=1/m$. For a posteriori estimate II, we used $h=1/8$ and $h=1/16$, with $k=h^2$.

Fig. 1

$\nu =0.1$

Fig. 2

$\nu =1$

Example 1.1 and 1.2: $u_h^k(x,t) \approx -t \sin (\pi x)$

Figures 1, 2 show the values of $C_{L^2L^2,L^2H_0^1}$ for Example 1.1–1.2, plotted out on log-linear coordinates. For $T>1$, the values of the proposed estimates are smaller than the other estimates. The two kinds of a posteriori estimates require the validated upper bound for the matrix two-norm of the corresponding unsymmetric dense matrices (e.g., $M_{\phi ,\psi }$), and most of the computational costs is due to this task. In Example 1.1, for $T=2$, a posteriori estimate I a matrix of size $14000$, but in a posteriori estimate II, we can attain our purpose with a matrix of size $896$ for $h=1/8$, and $7680$ for $h=1/16$. This fact shows, in the case of a posteriori estimate II, that it is not necessary to take special account of the stiff property of the ODEs coming from the semidiscretization.

Example 2.1 and 2.2: $u_h^k(x,t) \approx -2\sin (\pi t) \sin (\pi x)$

Figures 3, 4 show the values of $C_{L^2L^2,L^2H_0^1}$ for Example 2.1-2.2 (log-linear coordinates). For $T>1/2$, the values of the proposed estimates with $h=1/16$ are smaller than the other estimates. In Example 2.1, for $T=2$, a posteriori estimate I requires a matrix of size $8000$, but a posteriori estimate II requires only one of size $896$ for $h=1/8$ and size $7680$ for $h=1/16$. It is notable that the results of the proposed estimates show no exponential dependency for $T$. On the other hand, due to the stiffness of the corresponding ODEs, we were not successful in computing the inverse operator of a posteriori estimate I, except for the case where $T$ was very small.

Fig. 3

$\nu =0.1$

Fig. 4

$\nu =1$

6.2 Verification results for solutions of nonlinear parabolic equations

Applying the estimates (2), we implemented a numerical verification method to prove the existence of solutions for the nonlinear parabolic problems. As a prototype application, we considered the nonlinear parabolic initial-boundary-value problems of the form (43). In a similar way as in [8] for the elliptic case, we defined the fixed-point equation for a compact operator, which is equivalent to (43) with the Newton-type residual form, and derived a verification condition by applying the Schauder fixed-point theorem.

First, we considered the following residual equation for (43):

where

$$\begin{aligned} g(w)=w^2+\varepsilon ,\quad \varepsilon =(u_h^k)^2+f-\left( {\frac{\partial {u_h^k}}{\partial {t}}}-\nu \triangle {u_h^k}\right) . \end{aligned}$$

Note that if the approximate solution $u_h^k$ is close to the exact solution of (43), then $w\approx 0$, $\varepsilon \approx 0$, and $g(w)\approx 0$. Thus (44) can be rewritten as the following fixed-point equation of the compact map $F$:

$$\begin{aligned} w=\fancyscript{L}_t^{-1}g(w)=:F(w). \end{aligned}$$

(45)

Next, for any positive constants $\alpha$ and $\beta$, we define the candidate set $W_{\alpha ,\beta }$ as

$$\begin{aligned} W_{\alpha ,\beta }:={\left\{ {w \in V}~;~{\left\| {w}\right\| _{L^2H_0^1}\le \alpha ,\,\left\| {w}\right\| _{V^1L^2}\le \beta }\right\} }. \end{aligned}$$

From the Schauder fixed-point theorem, noting that the continuity of the map $F$ in the space $L^2H^1_0$, if the set $W_{\alpha ,\beta }$ satisfies

$$\begin{aligned} F(W_{\alpha ,\beta })\subset W_{\alpha ,\beta }, \end{aligned}$$

(46)

then a fixed point of (45) exists in the set $\overline{W_{\alpha ,\beta }}$, where $\overline{W_{\alpha ,\beta }}$ stands for the closure of the set $W_{\alpha ,\beta }$ in $L^2H^1_0$.

Now, for any $w \in W_{\alpha ,\beta }$, we obtain the following estimates:

$$\begin{aligned} \left\| {F(w)}\right\| _{L^2H_0^1}&\le C_{L^2L^2,L^2H_0^1}\left\| {g(w)}\right\| _{L^2L^2} \\&\le C_{L^2L^2,L^2H_0^1}\bigl (\left\| {w}\right\| _{L^4L^4}^2+\left\| {\varepsilon }\right\| _{L^2L^2}\bigr ). \nonumber \end{aligned}$$

(47)

Taking notice of the Sobolev embedding constants in one domensional case with $\varOmega =(0,1)$ and $J=(0,T)$ (cf. [15, p. 8]), we have

$$\begin{aligned} \left\| {w}\right\| _{L^4L^4}^4&\le \int \limits _J\left\| {w(t)}\right\| _{L^2(\varOmega )}^2\left\| {w(t)}\right\| _{L^\infty (\varOmega )}^2\,dt \\&\le \frac{1}{4}\int \limits _J\left\| {w(t)}\right\| _{L^2(\varOmega )}^2 \left\| {w(t)}\right\| _{H_0^1(\varOmega )}^2\,dt\\&\le \frac{1}{4}\left\| {w}\right\| _{L^\infty L^2}^2\left\| {w}\right\| _{L^2 H_0^1}^2 \\&\le \frac{T}{8}\left\| {w}\right\| _{V^1 L^2}^2\left\| {w}\right\| _{L^2 H_0^1}^2. \end{aligned}$$

Here, in order to get the last inequality, we have used the fact that in case of the function with 0 only at one endpoint, i.e., $t=0$, we can also apply the usual embedding theorem by considering a symmetric extension of the function on $(0,T)$ to $(0,2T)$. Therefore, from $w \in W_{\alpha ,\beta }$, we have

$$\begin{aligned} \left\| {g(w)}\right\| _{L^2L^2}&\le \sqrt{\frac{T}{8}}\left\| {w}\right\| _{V^1 L^2}\left\| {w}\right\| _{L^2 H_0^1} + \left\| {\varepsilon }\right\| _{L^2L^2} \le \sqrt{\frac{T}{8}}\alpha \beta + \left\| {\varepsilon }\right\| _{L^2L^2}. \end{aligned}$$

(48)

On the other hand, from [10, Lemma 2], the $V^1L^2$ norm of $F(w)$ is estimated by:

$$\begin{aligned} \left\| {F(w)}\right\| _{V^1L^2}&\le \left\| {\triangle _t F(w)}\right\| _{L^2L^2} \le \left\| {g(w)}\right\| _{L^2L^2} + 2\left\| {u_h^k}\right\| _{L^\infty L^\infty }\left\| {F(w)}\right\| _{L^2L^2}. \end{aligned}$$

Noting that the Poincaré constant can be taken as $\frac{1}{\pi }$ with $\varOmega =(0,1)$, we obtain, by (47)

$$\begin{aligned} \left\| {F(w)}\right\| _{L^2L^2}&\le \frac{1}{\pi }\left\| {F(w)}\right\| _{L^2H_0^1} \le \frac{1}{\pi }C_{L^2L^2,L^2H_0^1}\left\| {g(w)}\right\| _{L^2L^2}. \end{aligned}$$

Therefore, from (48), the following inequality holds:

$$\begin{aligned} \left\| {F(w)}\right\| _{V^1L^2}&\le \left( \frac{2}{\pi }C_{L^2L^2,L^2H_0^1}\left\| {u_h^k}\right\| _{L^\infty L^\infty }+1\right) \left( \alpha \beta \sqrt{\tfrac{T}{8}}+\left\| {\varepsilon }\right\| _{L^2L^2}\right) . \end{aligned}$$

By these inequalities, we have the following sufficient condition for (46):

$$\begin{aligned} \left\{ \begin{array}{lll} C_{L^2L^2,L^2H_0^1}\left( \alpha \beta \sqrt{\tfrac{T}{8}}+\left\| {\varepsilon }\right\| _{L^2L^2}\right) \le \alpha ,\\ \left( \frac{2}{\pi }C_{L^2L^2,L^2H_0^1}\left\| {u_h^k}\right\| _{L^\infty L^\infty }+1\right) \left( \alpha \beta \sqrt{\tfrac{T}{8}}+\left\| {\varepsilon }\right\| _{L^2L^2}\right) \le \beta . \end{array}\right. \end{aligned}$$

Thus, we obtain the verification condition for the existence of the solutions of (44). Since it holds that $w=u-u_h^k$, by solving the above simultaneous algebraic inequalities in $\alpha$ and $\beta$, we have error bounds of the form $\left\| {u-u_h^k}\right\| _{L^2H_0^1}\le \alpha$.

Fig. 5

Verification results: exact solution for $u(x,t) = 0.5 t \sin (\pi x)$, with $\nu =0.1$ (left), $\nu =1.0$ (right)

Fig. 6

Verification results: exact solution for $u(x,t) = \sin (\pi t) \sin (\pi x)$, with $\nu =0.1$ (left), $\nu =1.0$ (right)

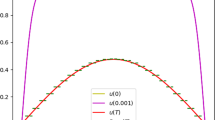
We now present the verification results for the solutions of (44), namely, $\alpha$, $\beta$, and the residual norm, $\left\| {\varepsilon }\right\| _{L^2L^2}$. In Fig. 5, we chose the function $f$ so that (43) has the exact solution $u(x,t) = 0.5 t \sin (\pi x)$, with $\nu =0.1$ and $\nu =1.0$, which correspond to Example 1.1 and Example 1.2, respectively, in the previous subsection. We show more results in Fig. 6, in which the function $f$ is chosen so that (43) has the exact solution $u(x,t) = \sin (\pi t) \sin (\pi x)$, with $\nu =0.1$ and $\nu =1.0$, which correspond to Example 2.1 and Example 2.2, respectively.

From these figures, it is seen that the error bounds increase in proportion to the residual norms. This property should be expected in our verification conditions. Namely, the validated accuracy of the present method is essentially dependent on the residual norm of the approximate solutions.

We see in the left side of Fig. 6, for the case $\nu =0.1$, that our verification method failed for $T>0.5$ with $h=1/8$. On the other hand, since $C_\varOmega (h)$ and the residual norm $\left\| {\varepsilon }\right\| _{L^2L^2}$ for the mesh size $h=1/16$ are smaller than in case of $h=1/8$, we succeeded in verification up to $T \le 1.25$. This fact shows that a smaller $h$ yields better verification, which should also be quite expected.

Remark 6.1

(Computer environment) All computations were carried out on a Dell Precision T7500 (Intel Xeon x5680, 72 GB of memory) with MATLAB R2010b. The computation errors have been taken into account by using INTLAB 6.0, a toolbox for self-validating algorithms, developed by Rump [14].

7 Conclusions

We propose a method to compute constructive a posteriori estimates of the inverse operators for parabolic initial-boundary-value problems. This method is based on the full-discretization quasi-Newton operator, as well as the constructive a priori error estimates for the Galerkin method, with an interpolation in time by effectively using the fundamental solution for the spatial semidiscretization. Our proposed new estimates (32) seem to be better and more robust than the previous estimates [10], as illustrated in the test problems. Moreover, by applying the method to some prototype examples, we illustrated that our method can be used to enclose solutions for nonlinear parabolic problems.