Abstract
We give a description of the center of the affine nilTemperley–Lieb algebra based on a certain grading of the algebra and on a faithful representation of it on fermionic particle configurations. We present a normal form for monomials, hence construct a basis of the algebra, and use this basis to show that the affine nilTemperley–Lieb algebra is finitely generated over its center. As an application, we obtain a natural embedding of the affine nilTemperley–Lieb algebra on N generators into the affine nilTemperley–Lieb algebra on \(N+1\) generators.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The main goal of this work is to describe the center of the affine nilTemperley–Lieb algebra \(\text {n}\widehat{\text {TL}}_{N}\) over any ground field. Only two tools are used: a fine grading on \(\text {n}\widehat{\text {TL}}_{N}\) and a representation of \(\text {n}\widehat{\text {TL}}_{N}\) on fermionic particle configurations on a circle. It is essential that this graphical representation be faithful (see [12, Prop. 9.1]). We provide an alternative proof of that fact by constructing a basis for \(\text {n}\widehat{\text {TL}}_{N}\) that is especially adapted to the problem. This basis has further advantages: It can be used to prove that the affine nilTemperley–Lieb algebra is finitely generated over its center. Also, it can be used to exhibit an explicit embedding of \(\text {n}\widehat{\text {TL}}_{N}\) into \(\text {n}\widehat{\text {TL}}_{N+1}\) defined on basis elements that otherwise would not be apparent, since the defining relations of these algebras are affine, and there is no embedding of the corresponding Coxeter graphs.
For a ground field \(\mathbb {k}\), the affine nilTemperley–Lieb algebra \(\text {n}\widehat{\text {TL}}_{N}\) is the unital associative \(\mathbb {k}\)-algebra given by N generators \(a_0,\ldots ,a_{N-1}\) and nil relations \(a_i^2=0\) and \(a_ia_{i\pm 1}a_i=0\) for all i. Generators that are far apart commute, i.e. \(a_ia_j=a_ja_i\) for \(i-j \ne \pm 1 \text { mod }N\). In these relations, the indices are interpreted modulo N so that the generators \(a_0\) and \(a_{N-1}\) are neighbours that do not commute. The subalgebra of \(\text {n}\widehat{\text {TL}}_{N}\) generated by \(a_1,\ldots ,a_{N-1}\) is the (finite) nilTemperley–Lieb algebra \( n TL _{N}\), as in [19]. The affine nilTemperley–Lieb algebra appears in many different settings, which we describe next.
-
1.
\(\text {n}\widehat{\text {TL}}_{N}\) is a quotient of the affine nilCoxeter algebra of type \(\tilde{\textsf {A}}_{N-1}\).
The affine nilCoxeter algebra \(\widehat{\mathsf U}_N\) of type \(\tilde{\textsf {A}}_{N-1}\) over a field \(\mathbb {k}\) is the unital associative algebra generated by elements \(u_i\), \(0 \le i \le N-1\), satisfying the relations \(u_i^2 = 0\); \(u_i u_j = u_j u_i\) for \(i - j \ne \pm 1\text { mod }N\); and \(u_i u_{i+1}u_i = u_{i+1}u_i u_{i+1}\) for \(1 \le i \le N-1\), where the subscripts are read modulo N. The algebra \(\text {n}\widehat{\text {TL}}_{N}\) is isomorphic to the quotient of \(\widehat{\mathsf U}_N\) obtained by imposing the additional relations \(u_i u_{i+1}u_i = u_{i+1}u_i u_{i+1}=0\) for \(1 \le i \le N-1\). The affine nilCoxeter algebra is closely connected with affine Schur functions, k-Schur functions, and the affine Stanley symmetric functions, which are related to reduced word decompositions in the affine symmetric group (see e.g. [14, 15]).
The nilCoxeter algebra \(\mathsf {U}_{N}\) has generators \(u_i, 1\le i \le N-1\), which satisfy the same relations as they do in \(\widehat{\mathsf {U}}_N\). It first appeared in work on the cohomology of flag varieties [3] and has played an essential role in studies on Schubert polynomials, Stanley symmetric functions, and the geometry of flag varieties (see for example [8, 11, 16, 17]). The definition of \(\mathsf {U}_N\) was inspired by the divided difference operators \(\partial _i\) on polynomials in variables \(\mathbf {x} = \{x_1, \dots , x_{N}\}\) defined by
$$\begin{aligned} \partial _i(f) = \frac{f(\mathbf x) - f(\sigma _i \mathbf {x})}{x_i - x_{i+1}}, \end{aligned}$$where the transposition \(\sigma _i\) fixes all the variables except for \(x_i\) and \(x_{i+1}\), which it interchanges. The operators \(\partial _i\) satisfy the nilCoxeter relations above, and applications of these relations enabled Fomin and Stanley [8] to recover known properties and establish new properties of Schubert polynomials.
The algebra \(\mathsf {U}_N\) belongs to a two-parameter family of algebras having generators \(u_i\), \(1 \le i \le N-1\), which satisfy the relations \(u_i u_j = u_j u_i\) for \(\vert i-j \vert > 1\) and \(u_i u_{i+1}u_i = u_{i+1}u_i u_{i+1}\) for \(1 \le i \le N-2\) from above, together with the relation \(u_i^2= \alpha u_i + \beta \) for all i, where \(\alpha , \beta \) are fixed parameters. In particular, the specialization \(\alpha =\beta =0\) yields the nilCoxeter algebra; \(\alpha =0\), \(\beta =1\) gives the standard presentation of the group algebra of the symmetric group \(\mathbb {k}\mathsf {S}_N\); and \(\alpha = q-1, \beta = q\) gives the Hecke algebra \(\mathsf {H}_N(q)\) of type \(\textsf {A}\).
Motivated by categorification results in [6], Khovanov [10] introduced restriction and induction functors \(\mathsf {F}_D\) and \(\mathsf {F}_{X}\) corresponding to the natural inclusion of algebras \(\mathsf {U}_N \hookrightarrow \mathsf {U}_{N+1}\) on the direct sum \(\mathcal C\) of the categories \(\mathcal C_N\) of finite-dimensional \(\mathsf {U}_N\)-modules. These functors categorify the Weyl algebra of differential operators with polynomial coefficients in one variable and correspond to the Weyl algebra generators \(\partial \) and x (derivative and multiplication by x), which satisfy the relation \(\partial x - x\partial = 1\).
Brichard [5] used a diagram calculus on cylinders to determine the dimension of the center of \(\mathsf {U}_N\) and to describe a basis of the center for which the multiplication is trivial. In this diagram calculus on N strands, the generator \(u_i\) corresponds to a crossing of the strands i and \(i+1\). The nil relation \(u_i^2=0\) is represented by demanding that any two strands may cross at most once; otherwise the diagram is identified with zero.
-
2.
\(\text {n}\widehat{\text {TL}}_{N}\) is a quotient of the negative part of the universal enveloping algebra of the affine Lie algebra
 .
.The negative part \(U^-\) of the universal enveloping algebra U of the affine Lie algebra
 has generators \(f_i\), \(0 \le i \le N-1\), which satisfy the Serre relations $$\begin{aligned}&f_i^2f_{i+ 1} - 2 f_i f_{i+ 1}f_i + f_{i + 1}f_i^2 = 0\\&\qquad =f_{i+1}^2f_{i} - 2 f_{i+ 1} f_{i}f_{i+ 1}+ f_{i }f_{i+ 1}^2\ \text { and }\ f_i f_j = f_j f_i\text { for }i-j \ne \pm 1\text { mod }N \end{aligned}$$
has generators \(f_i\), \(0 \le i \le N-1\), which satisfy the Serre relations $$\begin{aligned}&f_i^2f_{i+ 1} - 2 f_i f_{i+ 1}f_i + f_{i + 1}f_i^2 = 0\\&\qquad =f_{i+1}^2f_{i} - 2 f_{i+ 1} f_{i}f_{i+ 1}+ f_{i }f_{i+ 1}^2\ \text { and }\ f_i f_j = f_j f_i\text { for }i-j \ne \pm 1\text { mod }N \end{aligned}$$(all indices modulo N). Factoring \(U^-\) by the ideal generated by the elements \(f_i^2\), \(0 \le i \le N-1\), gives \(\text {n}\widehat{\text {TL}}_{N}\) whenever the characteristic of \(\mathbb {k}\) is different from 2.
-
3.
\(\text {n}\widehat{\text {TL}}_{N}\) acts on the small quantum cohomology ring of the Grassmannian.
As in [19, Sec. 2], (see also [12]), consider the cohomology ring \(\text {H}^\bullet (\text {Gr}(k,N))\) with integer coefficients for the Grassmannian \(\text {Gr}(k,N)\) of k-dimensional subspaces of \(\mathbb {k}^N\). It has a basis given by the Schubert classes \([\Omega _\lambda ]\), where \(\lambda \) runs over all partitions with k parts, the largest part having size \(N-k\). By recording the k vertical and \(N-k\) horizontal steps that identify the Young diagram of \(\lambda \) inside the northwest corner of a \(k \times (N-k)\) rectangle, such a partition corresponds to a (0, 1)-sequence of length N with k ones (resp. \(N-k\) zeros) in the positions corresponding to the vertical (respectively horizontal) steps.
As a \({\mathbb Z}[q]\)-module for an indeterminate q, the quantum cohomology ring of the Grassmannian is given by \(\text {qH}^\bullet (\text {Gr}(k,N))\ =\ {\mathbb Z}[q]\otimes _{\mathbb Z}\text {H}^\bullet (\text {Gr}(k,N))\) together with a q-multiplication. The \(\text {n}\widehat{\text {TL}}_{N}\)-action can be defined combinatorially on
$$\begin{aligned} \text {qH}^\bullet (\text {Gr}(k,N))\ \cong \ span _{{\mathbb Z}[q]} \,\{(0,1)\text {-sequences of length }N\text { with }k\text { ones}\} \end{aligned}$$as described in the next item, and the multiplication of two Schubert classes \([\Omega _\lambda ]\cdot [\Omega _\mu ]\) is equal to \(s_\lambda \cdot [\Omega _\mu ]\) where \(s_\lambda \) is a certain Schur polynomial in the generators of \(\text {n}\widehat{\text {TL}}_{N}\) as in [19, Cor. 8.3].
-
4.
\(\text {n}\widehat{\text {TL}}_{N}\) acts faithfully on fermionic particle configurations on a circle.
This is the graphical representation from [12] (see also [19]), which we use in our description of the center of \(\text {n}\widehat{\text {TL}}_{N}\). First, a (0, 1)-sequence with k ones is identified with a circular particle configuration having N positions, where the k particles are distributed at the position on the circle that corresponds to their position in the sequence, so that there is at most one particle at each position. On the space
$$\begin{aligned} span _{\mathbb {k}[q]} \,\{\text {fermionic particle configurations of }k\text { particles on a circle with }N\text { positions}\}, \end{aligned}$$the generators \(a_i\) of \(\text {n}\widehat{\text {TL}}_{N}\) act by sending a particle lying at position i to position \(i+1\). Additionally, the particle configuration is multiplied by \(\pm q\) when applying \(a_0\). The precise definition is given in Sect. 4, but here is a representative picture (Fig. 1).
-
5.
\(\text {n}\widehat{\text {TL}}_{N}\) appears as a subalgebra of the annihilation/creation algebra.
The finite nilTemperley–Lieb algebra is a subalgebra of the Clifford algebra having generators \(\{\xi _i,\xi _i^{*}\ |\ 0\le i\le N-1\}\) and relations \(\xi _i\xi _j+\xi _j\xi _i=0\), \(\xi _i^{*}\xi _j^{*}+\xi _j^{*}\xi _i^{*}=0\), \(\xi _i\xi _j^{*}+\xi _j^{*}\xi _i=\delta _{ij}\). The Clifford generators \(\xi _i\) (resp. \(\xi _i^{*}\)) act on the fermionic particle configurations by annihilation (resp. creation) of a particle at position i. The finite nilTemperley–Lieb algebra appears inside the Clifford algebra via \(a_i\mapsto \xi _{i+1}^{*}\xi _i\). As discussed in [12, Sec. 8], the affine nilTemperley–Lieb algebra is a q-deformation of this construction.
-
6.
\(\text {n}\widehat{\text {TL}}_{N}\) is the associated graded algebra of the affine Temperley–Lieb algebra.
The affine Temperley–Lieb algebra \(\widehat{ TL }_{N}(\delta )\) has the usual commuting relations and the relations \(a_ia_{i\pm 1}a_i=a_i\) and \(a_i^2=\delta a_i\) for some parameter \(\delta \in \mathbb {k}\) instead of the nil relations (where again all indices are mod N). It is a filtered algebra with its \(\ell \)th filtration space generated by all monomials of length \(\le \ell \). Since its associated graded algebra is \(\text {n}\widehat{\text {TL}}_{N}\) for any value of \(\delta \), elements of \(\text {n}\widehat{\text {TL}}_{N}\) can be identified with reduced expressions in \(\widehat{ TL }_{N}(\delta )\).
The diagrammatic structure of \(\widehat{ TL }_{N}(\delta )\) is given by the same pictures as for the Temperley–Lieb algebra, but now the diagrams are wrapped around the cylinder (see e.g. [7, 13]). The top and bottom of the cylinder each have N nodes. Monomials in the affine Temperley–Lieb algebra are represented by diagrams of N non-crossing strands, each connecting a pair of those 2N nodes. Multiplication of two monomials is realized by stacking the cylinders one on top of the other, and connecting and smoothing the strands. Whenever the strands form a circle, this is removed from the diagram at the expense of multiplying by the parameter \(\delta \). The relation \(a_ia_{i\pm 1}a_i=a_i\) corresponds to the isotopy between a strand that changes direction and a strand that is pulled straight.
In contrast, this diagrammatic realization for the affine nilTemperley–Lieb algebra would not respect isotopy: The relation \(a_ia_{i\pm 1}a_i=0\) implies that strands which change the direction are identified with zero. Nevertheless, the diagram of a reduced expression in \(\widehat{ TL }_{N}\) may be considered as an element of \(\text {n}\widehat{\text {TL}}_{N}\). Such a diagram consists of a number (possibly 0) of arcs that connect two nodes on the top of the cylinder, the same number of arcs connecting two nodes on the bottom, and arcs that connect a top node and a bottom one. The latter arcs wrap around the cylinder either all in a strictly clockwise direction or all in a strictly counterclockwise way. Since the multiplication of two such diagrams may give zero, we will not use this diagrammatic realization here.
We proceed as follows: In Sect. 2, we introduce the notation used in this article. The \({\mathbb Z}^N\)-grading of \(\text {n}\widehat{\text {TL}}_{N}\) is given is Sect. 3, and its importance for the description of the center is discussed. In Sect. 4, we give a detailed definition of the \(\text {n}\widehat{\text {TL}}_{N}\)-action on particle configurations on a circle. We also define special monomials that serve as the projections onto a single particle configuration (up to multiplication by \(\pm q\)). Theorem 4.5 of that section recalls [12, Prop. 9.1] stating that the representation is faithful. In [12], this fact is deduced from the finite nilTemperley–Lieb algebra case, as treated in [4] and [2, Prop. 2.4.1]. We give a complete, self-contained proof in Sect. 8. Our proof is elementary and relies on the construction of a basis. Section 5 contains the main result (Theorem 5.5) of this article:
Theorem
The center of \(\text {n}\widehat{\text {TL}}_{N}\) is the subalgebra

where the generator  is the sum of monomials
is the sum of monomials  corresponding to particle configurations given by increasing sequences
corresponding to particle configurations given by increasing sequences  of length k. The monomial
of length k. The monomial  sends particle configurations with \(n \ne k\) particles to 0 and acts on a particle configuration with k particles by projecting onto
sends particle configurations with \(n \ne k\) particles to 0 and acts on a particle configuration with k particles by projecting onto  and multiplying by \((-1)^{k-1}q\). Hence, \(\mathbf t _k\) acts as multiplication by q on the configurations with k particles.
and multiplying by \((-1)^{k-1}q\). Hence, \(\mathbf t _k\) acts as multiplication by q on the configurations with k particles.
Our \(N-1\) central generators \(\mathbf t _k\) are essentially the \(N-1\) central elements constructed by Postnikov. Lemma 9.4 of [19] gives an alternative description of \(\mathbf t _k\) as product of the kth elementary symmetric polynomial (with factors cyclically ordered) with the \((N-k)\)th complete homogeneous symmetric polynomial (with factors reverse cyclically ordered) in the noncommuting generators of \(\text {n}\widehat{\text {TL}}_{N}\). The above theorem shows that in fact these elements generate the entire center of \(\text {n}\widehat{\text {TL}}_{N}\). In Sect. 6, we establish that \(\text {n}\widehat{\text {TL}}_{N}\) is finitely generated over its center. In Sect. 7, we define a monomial basis for \(\text {n}\widehat{\text {TL}}_{N}\) indexed by pairs of particle configurations together with a natural number indicating how often the particles have been moved around the circle. A proof that this is indeed a basis of \(\text {n}\widehat{\text {TL}}_{N}\) can be found in Sect. 8. With this basis at hand, we obtain inclusions \(\text {n}\widehat{\text {TL}}_{N}\subset \text {n}\widehat{\text {TL}}_{N+1}\). The inclusions are not as obvious as those for the nilCoxeter algebra  having underlying Coxeter graph of type \(\textsf {A}_{N-1}\), since one cannot deduce them from embeddings of the affine Coxeter graphs. Our result, Theorem 7.1, reads as follows:
having underlying Coxeter graph of type \(\textsf {A}_{N-1}\), since one cannot deduce them from embeddings of the affine Coxeter graphs. Our result, Theorem 7.1, reads as follows:
Theorem
For all \(0\le m \le N-1\), there are unital algebra embeddings \(\varepsilon _m :\ \text {n}\widehat{\text {TL}}_{N}\rightarrow \text {n}\widehat{\text {TL}}_{N+1}\) given by
In Sect. 8, we show how to construct the monomial basis, namely by using a normal form algorithm that reorders the factors of a nonzero monomial. Our basis is reminiscent of the Jones normal form for reduced expressions of monomials in the Temperley–Lieb algebra, as discussed in [20], and is characterised in Theorem 8.6 as follows: (See also Theorem 7.5 which gives a different description.)
Theorem
(Normal form) Every nonzero monomial in the generators \(a_j\) of \(\text {n}\widehat{\text {TL}}_{N}\) can be rewritten uniquely in the form
with \(a^{(n)}_{i_\ell }\in \{1,a_0,a_1,\ldots ,a_{N-1}\}\text { for all }1\le n\le m,\ 1\le \ell \le k\), such that
The factors \(a_{i_1},\ldots ,a_{i_k}\) are determined by the property that the generator \(a_{i_\ell -1}\) does not appear to the right of \(a_{i_\ell }\) in the original presentation of the monomial. Alternatively, every nonzero monomial is uniquely determined by the following data from its action on the graphical representation:
-
the input particle configuration with the minimal number of particles on which it acts nontrivially,
-
the output particle configuration,
-
the power of q by which it acts.
For the proof of this result, we recall a characterisation of the nonzero monomials in \(\text {n}\widehat{\text {TL}}_{N}\) from [9]. Then we prove faithfulness of the graphical representation of \(\text {n}\widehat{\text {TL}}_{N}\) by describing explicitly the matrices representing our basis elements. Al Harbat [1] has recently described a normal form for fully commutative elements of the affine Temperley–Lieb algebra, which gives a different normal form when passing to \(\text {n}\widehat{\text {TL}}_{N}\).
Our results hold over an arbitrary ground field \(\mathbb {k}\), even one of characteristic 2, simply by ignoring signs in that case. In fact, our arguments work for any associative commutative unital ground ring R by replacing \(\mathbb {k}\)-vector spaces and \(\mathbb {k}\)-algebras with free R-modules and R-algebras, respectively. In particular, the affine nilTemperley–Lieb algebra over \(\mathbb {k}\) is replaced by the R-algebra with the same generators and relations, and the polynomial ring \(\mathbb {k}[q]\) is replaced by R[q]. We can even drop the assumption that the ring R is commutative if we slightly modify the statements about the center. This is possible because our arguments mainly rely on investigating monomials in the generators of \(\text {n}\widehat{\text {TL}}_{N}\). However, for simplicity we have chosen to assume \(\mathbb {k}\) is a field throughout the article.
2 Notation
Let \(\mathbb {k}\) be any field, and assume N is a positive integer. The affine nilTemperley–Lieb algebra \(\text {n}\widehat{\text {TL}}_{N}\) of rank N is the unital associative \(\mathbb {k}\)-algebra generated by elements \(a_0,\ldots ,a_{N-1}\) subject to the defining relations

where all indices are taken modulo N, so in particular \(a_{N-1}a_0a_{N-1}=a_0a_{N-1}a_0=0\). The finite nilTemperley–Lieb algebra
\( n TL _{N}\), as defined in [19], is the subalgebra of \(\text {n}\widehat{\text {TL}}_{N}\) generated by \(a_1,\ldots ,a_{N-1}\) (or in fact, by any \(N-1\) of the generators \(a_i\)). We adopt the convention that \( n TL _{1} =\mathbb {k}1\). We fix the following notation for monomials in \(\text {n}\widehat{\text {TL}}_{N}\) and \( n TL _{N}\): For an ordered index sequence  with \(0\le j_1,\ldots ,j_m\le N-1\), we define the ordered monomial
with \(0\le j_1,\ldots ,j_m\le N-1\), we define the ordered monomial  . Unless otherwise specified, we use the letters i, j
for indices from \({\mathbb Z}/N{\mathbb Z}\); in particular, we often identify the indices 0 and N.
. Unless otherwise specified, we use the letters i, j
for indices from \({\mathbb Z}/N{\mathbb Z}\); in particular, we often identify the indices 0 and N.
Throughout we will assume \(N\ge 3\).
3 Gradings
One of the ingredients needed in Sect. 5 to study the center of \(\text {n}\widehat{\text {TL}}_{N}\) is a grading on the algebra.
Gradings faciliate the computation of the center of an algebra, as the following standard result reduces the work to determining homogeneous central elements.
Lemma 3.1
If \(A=\bigoplus _{g\in G} A_g\) is an algebra graded by some abelian group G, then the center of A is homogeneous, i.e. it inherits the grading.
Proof
Let \(a=\sum _{g\in G}a_g\) be a central element of the graded algebra \(A=\bigoplus _{g\in G} A_g\). We have for \(b_h\in A_h\) that
Since this equality must hold in every graded component, we get \(a_g b_h = b_h a_g\) for all homogeneous elements \(b_h\). Now take any element \(b=\sum \limits _{h\in G}b_h\) in A, then
hence \(a_g\) is central. \(\square \)
Since the defining relations are homogeneous, both \(\text {n}\widehat{\text {TL}}_{N}\) and \( n TL _{N}\) have a \({\mathbb Z}\)-grading by the length of a monomial, i.e. all generators \(a_i\) have \({\mathbb Z}\)-degree 1. This can be refined to a \({\mathbb Z}^N\)-grading by assigning to the generator \(a_i\) the degree \(\zeta _i\), the ith standard basis vector in \({\mathbb Z}^N\). In either grading, we say that the degree 0 part of an element in \(\text {n}\widehat{\text {TL}}_{N}\) or \( n TL _{N}\) is its constant term.
The \({\mathbb Z}^N\)-grading is finer than the \({\mathbb Z}\)-grading in the sense that any \({\mathbb Z}\)-graded component of degree different from 0 decomposes into a sum of \({\mathbb Z}^N\)-graded components of strictly smaller dimension.
Remark 3.2
Why do we exclude the case of \(N\le 2\) from our considerations? For \(N = 1,2\), there are isomorphisms \(\text {n}\widehat{\text {TL}}_{N}\cong n TL _{N+1}\), and in these cases the center is uninteresting. The algebra \(\text {n}\widehat{\text {TL}}_{1}\) is 2-dimensional and commutative; while \(\text {n}\widehat{\text {TL}}_{2}\) has dimension 5, and its center can be computed by hand making use of Lemma 3.1 and can be shown to be the \(\mathbb {k}\)-span of \(1, a_0a_1, a_1a_0\).
Remark 3.3
The affine (or finite) Temperley–Lieb algebra, which has relations \(a_i a_j = a_j a_i\) for \(i-j \ne \pm 1\ (\text {mod }N)\), \(a_ia_{i\pm 1}a_i=a_i\), and \(a_i^2=\delta a_i\) for some \(\delta \in \mathbb {k}\), is a filtered algebra with respect to the length filtration. For this algebra, the \(\ell \)th filtration space is generated by all monomials of length \({\le }\ell \). Its associated graded algebra is \(\text {n}\widehat{\text {TL}}_{N}\) (or \( n TL _{N}\)). Thus, \(\text {n}\widehat{\text {TL}}_{N}\) is infinite dimensional when \(N \ge 3\), while \( n TL _{N}\) has dimension equal to the Nth Catalan number \(\frac{1}{N+1}{{2N} \atopwithdelims ()N}\).
4 A faithful representation
The second ingredient we use to determine the center is a faithful representation of \(\text {n}\widehat{\text {TL}}_{N}\). Here we recall the definition of the representation from [12] and describe its graphical realization, which is very convenient to work with.
Fix a basis \(v_1,\ldots , v_N\) of \(\mathbb {k}^N\). Consider the vector space \(\textsf {V}=\bigoplus \limits _{k=0}^N\left( \mathbb {k}[q] \otimes \bigwedge ^k\mathbb {k}^N\right) \). It has a standard \(\mathbb {k}[q]\)-basis consisting of wedges

for all \(0\le k\le N\), where the basis element of \(\mathbb {k}=\bigwedge ^0\mathbb {k}^N\) is denoted \(v(\emptyset )\). Throughout the rest of the paper, all tensor products are taken over \(\mathbb {k}\), and we omit the tensor symbol in \(\mathbb {k}[q]\)-linear combinations of wedges.
Remark 4.1
The indices of the vectors \(v_j\) should be interpreted modulo N. We make no distinction between \(v_0\) and \(v_N\) and often use the two interchangeably.
It is helpful to visualize the basis elements  as particle configurations having \(0\le k\le N\) particles arranged on a circle with N positions, where there is at most one particle at each site, as pictured below for \(N=8\) and \(v(1,5,6)=v_1\wedge v_5\wedge v_6\) (Fig. 2). The vector \(v(\emptyset )\) corresponds to the configuration with no particles. Then \(\textsf {V}\) is the \(\mathbb {k}[q]\)-span of such circular particle configurations.
as particle configurations having \(0\le k\le N\) particles arranged on a circle with N positions, where there is at most one particle at each site, as pictured below for \(N=8\) and \(v(1,5,6)=v_1\wedge v_5\wedge v_6\) (Fig. 2). The vector \(v(\emptyset )\) corresponds to the configuration with no particles. Then \(\textsf {V}\) is the \(\mathbb {k}[q]\)-span of such circular particle configurations.
There is an action of the affine nilTemperley–Lieb algebra \(\text {n}\widehat{\text {TL}}_{N}\) defined on the basis vectors  of \(\textsf {V}\) as follows:
of \(\textsf {V}\) as follows:
Definition 4.2
For \(1\le j\le N-1\),

For the action of \(a_0\), note that \(v_N\) appears in the basis element  if and only if it occurs in the last position, i.e. \(v_{i_k}=v_N\), and define
if and only if it occurs in the last position, i.e. \(v_{i_k}=v_N\), and define

The sign appears in  because of the equality
because of the equality
Remark 4.3
It follows that  if the sequence
if the sequence  contains
contains  or if it does not contain j. In other words,
or if it does not contain j. In other words,  acts by replacing
acts by replacing  by
by  . If this creates a wedge expression with two factors equal to
. If this creates a wedge expression with two factors equal to  , the result is zero. Thus, for any monomial
, the result is zero. Thus, for any monomial  there is a unique increasing sequence
there is a unique increasing sequence  with k minimal on which the monomial acts nontrivially.
with k minimal on which the monomial acts nontrivially.
In the graphical description, \(a_j\) moves a particle clockwise from position j to position \(j+1\), and one records ‘passing position 0’ by multiplying by \(\pm q\) as illustrated by the particle configurations in Fig. 3.
It is easy to verify that the defining relations for \(\text {n}\widehat{\text {TL}}_{N}\) hold for this action, assuming that \(N\ge 3\). Hence we obtain
Lemma 4.4
-
(a)
Definition 4.2 gives a representation of \(\text {n}\widehat{\text {TL}}_{N}\) on \(\textsf {V}\).
-
(b)
The number of wedges (i.e., the number of particles) remains constant under the action of the generators \(a_i\), so that \(\textsf {V}={\bigoplus _{k=0}^N\left( \mathbb {k}[q] \otimes \bigwedge ^k\mathbb {k}^N\right) }\) is a direct sum decomposition of \(\textsf {V}\) as an \(\text {n}\widehat{\text {TL}}_{N}\)-module.
The following crucial statement is taken from [2, Prop. 2.4.1] and [12, Prop. 9.1.(2)]. We will give a detailed proof adapted to our notation in Sect. 8.
Theorem 4.5
The action from Definition 4.2 gives a faithful representation of \(\text {n}\widehat{\text {TL}}_{N}\) on \(\textsf {V}\) when \(N \ge 3\).
From now on, we will identify elements of \(\text {n}\widehat{\text {TL}}_{N}\) with their action on the particle configurations of the graphical representation.
Remark 4.6
The spaces \(\mathbb {k}[q]\otimes \bigwedge ^0\mathbb {k}^N\) and \(\mathbb {k}[q] \otimes \bigwedge ^N\mathbb {k}^N\) are trivial summands in \(\textsf {V}\) on which every generator \(a_i\) acts as 0, and so they may be ignored when proving Theorem 4.5.
For a standard basis element  of \(1 \le k \le N-1\) wedges corresponding to an increasing sequence
of \(1 \le k \le N-1\) wedges corresponding to an increasing sequence  , the next lemma defines a certain monomial
, the next lemma defines a certain monomial  that projects
that projects  and sends
and sends  to zero for
to zero for  . Before stating the result, we give an example to demonstrate in the graphical description how this projector will be defined.
. Before stating the result, we give an example to demonstrate in the graphical description how this projector will be defined.
Example 4.7
Let \(N=8\), and consider the particle configuration  With \(a(\widehat{1\ 5\ 6})\ =\ (a_0 a_7)\cdot (a_4 a_3 a_2)\cdot (a_1 a_5 a_6)\) we obtain \(a(\widehat{1\ 5\ 6})\cdot \ v_1\wedge v_5\wedge v_6\ =\ (-1)^2 q\cdot v_1\wedge v_5\wedge v_6\), which looks as follows in the graphical description (Fig. 4).
With \(a(\widehat{1\ 5\ 6})\ =\ (a_0 a_7)\cdot (a_4 a_3 a_2)\cdot (a_1 a_5 a_6)\) we obtain \(a(\widehat{1\ 5\ 6})\cdot \ v_1\wedge v_5\wedge v_6\ =\ (-1)^2 q\cdot v_1\wedge v_5\wedge v_6\), which looks as follows in the graphical description (Fig. 4).
The factor \(a_1a_5a_6\) moves every particle one step forward clockwise. It is critical that we start by moving the particle at position 6 before moving the particle at position 5, as otherwise the result would be zero. But since there is a ‘gap’ at position 7, we can move the particle from site 6 to 7, and afterwards the particle from site 5 to 6, without obtaining zero. The assumption that \(k<N\) ensures such a gap always exists.
After applying \(a_1a_5a_6\), the particles are at positions 2, 6, and 7. The particle previously at position 5 is now at position 6, which is where we want a particle to be. The particle currently at position 2 can be moved to position 5 by applying the product \(a_4 a_3 a_2\). The particle now at position 7 can be moved by \(a_0 a_7\) to position 1. Hence, the result of applying \((a_0 a_7)\cdot (a_4 a_3 a_2) \cdot (a_1 a_5 a_6)\) is the same particle configuration as the original one. However, the answer must be multiplied by \(\pm q\), since applying \(a_0 a_7\) involves crossing the zero position once. To determine the sign, note from Definition 4.2 that \((a_0 a_7) \cdot (a_4 a_3 a_2) \cdot (a_1 a_5 a_6)(v_1 \wedge v_5 \wedge v_6) = q \cdot v_5 \wedge v_6 \wedge v_1 = (-1)^2 q \cdot v_1 \wedge v_5 \wedge v_6\), so the sign is \(+\).
Now we describe the general procedure:
Lemma 4.8
Assume  is a particle configuration, where
is a particle configuration, where  is an increasing sequence and \(1 \le k \le N-1\). Then there exists an index \(\ell \) such that \(i_\ell +1<i_{\ell +1}\) (or \(i_{k}+1<i_1\)), i.e. the sequence has a ‘gap’ between \(i_\ell \) and \(i_{\ell +1}\). Split the sequence
is an increasing sequence and \(1 \le k \le N-1\). Then there exists an index \(\ell \) such that \(i_\ell +1<i_{\ell +1}\) (or \(i_{k}+1<i_1\)), i.e. the sequence has a ‘gap’ between \(i_\ell \) and \(i_{\ell +1}\). Split the sequence  into the two parts \(\{i_1<\cdots < i_\ell \}\) and \(\{i_{\ell +1}<\cdots <i_k\}\). Set
into the two parts \(\{i_1<\cdots < i_\ell \}\) and \(\{i_{\ell +1}<\cdots <i_k\}\). Set

where the indices are modulo N in the factor \((a_{i_{1}-1}a_{i_{1}-2}\ldots a_{i_k+2}a_{i_k+1})\). Then

and  has
has  -degree \((1,1,\ldots ,1)\).
-degree \((1,1,\ldots ,1)\).
Proof
The assertions can be seen using the graphical realization of \(\textsf {V}\). The terms in the second line of equation (*) move a particle at site  one step forward to \(i_j+1\) for each j, while the terms in the first line send the particle from \(i_j+1\) to the original position of \(i_{j+1}\).
one step forward to \(i_j+1\) for each j, while the terms in the first line send the particle from \(i_j+1\) to the original position of \(i_{j+1}\).
Consider first  By applying
By applying  , every particle is first moved clockwise by one position. By our choice of the index \(i_\ell \), we avoid mapping the whole particle configuration to zero. After that step, every particle is moved by one of the factors \((a_{i_{s+1}-1}a_{i_{s+1}-2}\ldots a_{i_s+2}a_{i_s+1})\) to the original position of its successor in the sequence
, every particle is first moved clockwise by one position. By our choice of the index \(i_\ell \), we avoid mapping the whole particle configuration to zero. After that step, every particle is moved by one of the factors \((a_{i_{s+1}-1}a_{i_{s+1}-2}\ldots a_{i_s+2}a_{i_s+1})\) to the original position of its successor in the sequence  , so the particle configuration remains the same. One of the particles has passed the zero position, so we have to multiply by \(\pm q\). Definition 4.2 tells us the appropriate sign is \((-1)^{k-1}\).
, so the particle configuration remains the same. One of the particles has passed the zero position, so we have to multiply by \(\pm q\). Definition 4.2 tells us the appropriate sign is \((-1)^{k-1}\).
Now consider  for
for  The monomial \((a_{i_{\ell +1}}a_{i_{\ell +2}}\ldots a_{i_{k-1}}a_{i_{k}})\cdot (a_{i_1}a_{i_{2}}\ldots a_{i_{\ell -1}}a_{i_\ell })\) expects a particle at each of the sites \(i_1,\ldots , i_k\), so if any of these positions is empty in
The monomial \((a_{i_{\ell +1}}a_{i_{\ell +2}}\ldots a_{i_{k-1}}a_{i_{k}})\cdot (a_{i_1}a_{i_{2}}\ldots a_{i_{\ell -1}}a_{i_\ell })\) expects a particle at each of the sites \(i_1,\ldots , i_k\), so if any of these positions is empty in  , the result of applying
, the result of applying  is zero. If the positions
is zero. If the positions  are already filled, and there is an additional particle somewhere, multiplication by \((a_{i_{\ell +1}-1}a_{i_{\ell +1}-2}\ldots a_{i_\ell +2}a_{i_\ell +1})\) will cause two particles to be at the same position, hence the result is again zero.
are already filled, and there is an additional particle somewhere, multiplication by \((a_{i_{\ell +1}-1}a_{i_{\ell +1}-2}\ldots a_{i_\ell +2}a_{i_\ell +1})\) will cause two particles to be at the same position, hence the result is again zero.
Since every \(a_j\) appears in  exactly once, the monomial
exactly once, the monomial  has
has  -degree \((1,1, \ldots , 1)\). \(\square \)
-degree \((1,1, \ldots , 1)\). \(\square \)
Example 4.9
In the previous example, \(N = 8\),  , and we may assume the two subsequences are (1) and (5, 6). Then the terms in the second line of (*) are \((a_5 a_6)\cdot (a_1) = a_1 a_5 a_6\). The term corresponding to \(j = 1\) in the product on the first line of (*) is \(a_4 a_3 a_2\), and the expression corresponding to \(j=2\) is empty, hence taken to be 1. The first factor on the first line is \(a_0 a_7\). Thus, for
, and we may assume the two subsequences are (1) and (5, 6). Then the terms in the second line of (*) are \((a_5 a_6)\cdot (a_1) = a_1 a_5 a_6\). The term corresponding to \(j = 1\) in the product on the first line of (*) is \(a_4 a_3 a_2\), and the expression corresponding to \(j=2\) is empty, hence taken to be 1. The first factor on the first line is \(a_0 a_7\). Thus, for  ,
,  , as in Example 4.7. If the gap between 6 and 0 is used instead, the right-hand factor of the second line is
, as in Example 4.7. If the gap between 6 and 0 is used instead, the right-hand factor of the second line is  and the left-hand factor is 1. The factors in the first line remain the same, and so one obtains the same expression for
and the left-hand factor is 1. The factors in the first line remain the same, and so one obtains the same expression for  .
.
Remark 4.10
Because  is a faithful module,
is a faithful module,  is, as an element in
is, as an element in  (i.e. up to reordering according to the defining relations), uniquely determined by the increasing sequence
(i.e. up to reordering according to the defining relations), uniquely determined by the increasing sequence  One can read off
One can read off  from
from  as follows: In the defining equation (*) of
as follows: In the defining equation (*) of  the factors in the first line are pairwise commuting. The underlying subsequence
the factors in the first line are pairwise commuting. The underlying subsequence  corresponding to the factor \(a_{i_{s+1}-1}a_{i_{s+1}-2}\ldots a_{i_s+2}a_{i_s+1}\) of
corresponding to the factor \(a_{i_{s+1}-1}a_{i_{s+1}-2}\ldots a_{i_s+2}a_{i_s+1}\) of  is a decreasing sequence. After all such decreasing sequences are removed from
is a decreasing sequence. After all such decreasing sequences are removed from  what remains is a product of generators
what remains is a product of generators  with an increasing subsequence of indices or a product of two such subsequences corresponding to the factors in the second line. This is
with an increasing subsequence of indices or a product of two such subsequences corresponding to the factors in the second line. This is  . Given any monomial
. Given any monomial  of \({\mathbb Z}^N\)-degree \((1,\ldots ,1)\), one can rewrite it using the relations in
of \({\mathbb Z}^N\)-degree \((1,\ldots ,1)\), one can rewrite it using the relations in  so that it is of the form
so that it is of the form  for some increasing sequence
for some increasing sequence  . Then
. Then  is the unique standard basis element upon which
is the unique standard basis element upon which  acts by multiplication by \(\pm q\).
acts by multiplication by \(\pm q\).
5 Description of the center
In this section, we give an explicit description of the center \({\textsf {C}}_N\) of \(\text {n}\widehat{\text {TL}}_{N}\). We start with the following initial characterisation of the central elements:
Lemma 5.1
Any central element c in \(\text {n}\widehat{\text {TL}}_{N}\) with constant term 0 is a linear combination of monomials  where every generator \(a_i\), \(0\le i\le N-1\), appears at least once. In particular, a homogeneous nonconstant central element c has \({\mathbb Z}\)-degree at least N.
where every generator \(a_i\), \(0\le i\le N-1\), appears at least once. In particular, a homogeneous nonconstant central element c has \({\mathbb Z}\)-degree at least N.
Proof
Assume  , where
, where  for all
for all  . By Lemma 3.1, we can assume c is a homogeneous central element with respect to the \({\mathbb Z}^N\)-grading. By our assumption, \(c\notin \mathbb {k}\). For all i, we need to show that \(a_i\) occurs in each monomial
. By Lemma 3.1, we can assume c is a homogeneous central element with respect to the \({\mathbb Z}^N\)-grading. By our assumption, \(c\notin \mathbb {k}\). For all i, we need to show that \(a_i\) occurs in each monomial  appearing in c. Without loss of generality, we show this for \(i=0\). If some summand is missing \(a_0\), then no summand contains \(a_0\) because c is homogeneous. Hence
appearing in c. Without loss of generality, we show this for \(i=0\). If some summand is missing \(a_0\), then no summand contains \(a_0\) because c is homogeneous. Hence  and
and  for all
for all  with
with  , and since \(a_0 c= c a_0\), none of the
, and since \(a_0 c= c a_0\), none of the  can contain the factor \(a_1\) either, as otherwise the factor \(a_0\) cannot pass through c from left to right (so also \(a_{N-1}\) cannot be contained in the
can contain the factor \(a_1\) either, as otherwise the factor \(a_0\) cannot pass through c from left to right (so also \(a_{N-1}\) cannot be contained in the  ). Proceeding inductively, we see that all
). Proceeding inductively, we see that all  must be a constant, contrary to our assumption. \(\square \)
must be a constant, contrary to our assumption. \(\square \)
The next proposition states that on the standard wedge basis vector  of \(\textsf {V}\), any central element acts via multiplication by a polynomial \(p_k\in \mathbb {k}[q]\) that only depends on the length
of \(\textsf {V}\), any central element acts via multiplication by a polynomial \(p_k\in \mathbb {k}[q]\) that only depends on the length  of the increasing sequence
of the increasing sequence  . In other words, the decomposition of \(\textsf {V}\) into the summands \(\mathbb {k}[q] \otimes \bigwedge ^k\mathbb {k}^N\) is a decomposition with respect to different central characters (apart from the two trivial summands for \(k\in \{0,N\}\)).
. In other words, the decomposition of \(\textsf {V}\) into the summands \(\mathbb {k}[q] \otimes \bigwedge ^k\mathbb {k}^N\) is a decomposition with respect to different central characters (apart from the two trivial summands for \(k\in \{0,N\}\)).
Proposition 5.2
For any central element \(c\in \text {n}\widehat{\text {TL}}_{N}\) and all increasing sequences  with fixed length k, there is some element \(p_k\in \mathbb {k}[q]\) such that
with fixed length k, there is some element \(p_k\in \mathbb {k}[q]\) such that  .
.
Proof
We may assume c is a nonconstant \({\mathbb Z}^N\)-homogeneous central element of \(\text {n}\widehat{\text {TL}}_{N}\). For \(k\in \{0,N\}\), the action of a generator \(a_i\) on a monomial of length k is 0, so \(p_k=0\) for such values of k. Now consider \(1\le k\le N-1\), and suppose that  is an increasing sequence of length k. According to Lemma 4.4 (b), the number of wedges in a vector remains constant under the action of the \(a_i\). Hence
is an increasing sequence of length k. According to Lemma 4.4 (b), the number of wedges in a vector remains constant under the action of the \(a_i\). Hence  for some polynomials
for some polynomials  . We want to prove that
. We want to prove that  for all
for all  .
.
We have shown in Lemma 4.8 that to each increasing sequence  there corresponds a monomial
there corresponds a monomial  that allows us to select a single basis vector:
that allows us to select a single basis vector:

Thus, for  we see that
we see that

implying  for
for  . Hence, we may assume for each increasing sequence
. Hence, we may assume for each increasing sequence  that
that  for some polynomial
for some polynomial  .
.
Now it is left to show that  for all
for all  with
with  . It is enough to verify this for
. It is enough to verify this for  ,
,  that differ in exactly one entry, i.e. \(i_s=i\), \(i_s^{\prime }=i+1\), and \(i_\ell =i_\ell ^{\prime }\) for all \(\ell \ne s\), for some \(1\le s\le k\) and \(i\in {\mathbb Z}/N{\mathbb Z}\). If \(1\le i\le N-1\), we have
that differ in exactly one entry, i.e. \(i_s=i\), \(i_s^{\prime }=i+1\), and \(i_\ell =i_\ell ^{\prime }\) for all \(\ell \ne s\), for some \(1\le s\le k\) and \(i\in {\mathbb Z}/N{\mathbb Z}\). If \(1\le i\le N-1\), we have

and if \(i=0\), we get

Hence,  , and this common polynomial is the desired polynomial \(p_k\). \(\square \)
, and this common polynomial is the desired polynomial \(p_k\). \(\square \)
Corollary 5.3
Any central element in \(\text {n}\widehat{\text {TL}}_{N}\) with constant term 0 acts on a standard basis vector  as multiplication by an element of \(q\mathbb {k}[q]\).
as multiplication by an element of \(q\mathbb {k}[q]\).
Proof
According to Lemma 5.1, each summand of such a central element must contain the factor \(a_0\), and \(a_0\) acts on a wedge product by 0 or multiplication by \(\pm q\). \(\square \)
Now we are ready to introduce nontrivial central elements in \(\text {n}\widehat{\text {TL}}_{N}\). For each \(1\le k\le N-1\), set

where the monomials  correspond to increasing sequences
correspond to increasing sequences  of length k as defined in Lemma 4.8.
of length k as defined in Lemma 4.8.
Example 5.4
In \(\text {n}\widehat{\text {TL}}_{3}\):
In \(\text {n}\widehat{\text {TL}}_{4}\):
In the graphical realization of \(\textsf {V}\), \(\mathbf t _k\) acts by annihilating all particle configurations whose number of particles is different from k. For particle configurations having k particles, every particle is moved clockwise to the original site of the next particle. Hence, the particle configuration itself remains fixed by the action of \(\mathbf t _k\) (and it is multiplied with \((-1)^{2(k-1)}q =q\), since a particle has been moved through position 0). All the \(\mathbf t _k\) have \({\mathbb Z}^N\)-degree equal to \((1,\ldots ,1)\) and \({\mathbb Z}\)-degree equal to N. Any monomial whose \({\mathbb Z}^N\)-degree is \((1,\ldots ,1)\) occurs as a summand in some central element (after possibly reordering the factors), and the number of summands of \(\mathbf t _k\) equals \(\left( {\begin{array}{c}N\\ k\end{array}}\right) = dim (\bigwedge ^k\mathbb {k}^N)\); see Remark 4.10.
Theorem 5.5
-
1.
The \(\mathbf t _k\) are central for all \(1\le k\le N-1\), and the center of \(\text {n}\widehat{\text {TL}}_{N}\) is generated by 1 and the \(\mathbf t _k\), \(1\le k\le N-1\).
-
2.
The subalgebra generated by \(\mathbf t _k\) is isomorphic to the polynomial ring \(\mathbb {k}[q]\) for all \(1\le k\le N-1\). Moreover \(\mathbf t _k\mathbf t _\ell =0\) for all \(k\ne \ell \). Hence the center of \(\text {n}\widehat{\text {TL}}_{N}\) is the subalgebra
$$\begin{aligned} {\textsf {C}}_N\ =\ \mathbb {k}\oplus \mathbf t _1\mathbb {k}[\mathbf t _1]\oplus \cdots \oplus \mathbf t _{N-1}\mathbb {k}[\mathbf t _{N-1}]\ \cong \ \frac{\mathbb {k}[\mathbf t _1,\ldots ,\mathbf t _{N-1}]}{(\mathbf t _k\mathbf t _\ell \mid k\ne \ell )}. \end{aligned}$$
Proof
-
1.
The action of \(\mathbf t _k\) on \(\textsf {V}\) is the projection onto the \(\text {n}\widehat{\text {TL}}_{N}\)-submodule \(\mathbb {k}[q] \otimes \bigwedge ^k\mathbb {k}^N\) followed by multiplication by q. This commutes with the action of every other element of \(\text {n}\widehat{\text {TL}}_{N}\). Since \(\textsf {V}\) is a faithful module, \(\mathbf t _k\) commutes with any element of \(\text {n}\widehat{\text {TL}}_{N}\). As we have seen in Proposition 5.2, any central element c without constant term acts on the summand \(\mathbb {k}[q] \otimes \bigwedge ^k\mathbb {k}^N\) via multiplication by some polynomial \(p^c_{k}\in q\mathbb {k}[q]\). Once again using the faithfulness of \(\textsf {V}\), we get that \(c = \sum _{k=1}^{N-1} p_k^c(\mathbf t _k)\).
-
2.
Recall that \(\mathbb {k}[q] \otimes \bigwedge ^k\mathbb {k}^N\) is a free \(\mathbb {k}[q]\)-module of rank \({N \atopwithdelims ()k}\). Since \(\mathbf t _k\) acts by multiplication with q on that module, the subalgebra of \(\text {n}\widehat{\text {TL}}_{N}\) generated by \(\mathbf t _k\) must be isomorphic to the polynomial ring \(\mathbb {k}[q]\). Since
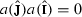 for all
for all  we get \(\mathbf t _k \mathbf t _\ell =0\) for \(k \ne \ell \), as they consist of pairwise distinct summands.\(\square \)
we get \(\mathbf t _k \mathbf t _\ell =0\) for \(k \ne \ell \), as they consist of pairwise distinct summands.\(\square \)
Theorem 5.5 enables us to describe the \(\mathbb {k}\)-algebra \( End _{\text {n}\widehat{\text {TL}}_{N}}(\textsf {W})\) of \(\text {n}\widehat{\text {TL}}_{N}\)-endomorphisms of the space of nontrivial particle configurations \(\textsf {W}:=\bigoplus _{k=1}^{N-1}\left( \mathbb {k}[q] \otimes \bigwedge ^k\mathbb {k}^N\right) \subset \ \textsf {V}\). We first observe that on \(\textsf {W}\) multiplication by q is given by the action of a central element in \({\textsf {C}}_N\), therefore it is justified to speak about \(\mathbb {k}[q]\)-linearity of a \(\text {n}\widehat{\text {TL}}_{N}\)-endomorphism of \(\textsf {W}\).
Lemma 5.6
\( End _{\text {n}\widehat{\text {TL}}_{N}}(\textsf {W})\subset End _{\mathbb {k}[q]}(\textsf {W})\), hence any \(\text {n}\widehat{\text {TL}}_{N}\)-module endomorphism \(\varphi \) of \(\textsf {W}\) is \(\mathbb {k}[q]\)-linear.
Proof
Observe that \(\sum _{k=1}^{N-1}\mathbf t _k\in \text {n}\widehat{\text {TL}}_{N}\) acts by multiplication by q on every element in \(\textsf {W}\). Therefore multiplication by q commutes with the application of every \(\varphi \in End _{\text {n}\widehat{\text {TL}}_{N}}(\textsf {W})\).
\(\square \)
Proposition 5.7
The endomorphism algebra \( End _{\text {n}\widehat{\text {TL}}_{N}}(\textsf {W})\) is isomorphic to a direct sum of \(N-1\) polynomial algebras \(\mathbb {k}[T_1]\oplus \cdots \oplus \mathbb {k}[T_{N-1}]\).
Proof
The proof is very similar to that of Proposition 5.2. First we show that  is a \(\mathbb {k}[q]\)-linear multiple of
is a \(\mathbb {k}[q]\)-linear multiple of  for any \(\varphi \in End _{\text {n}\widehat{\text {TL}}_{N}}(\textsf {W})\) and any increasing sequence
for any \(\varphi \in End _{\text {n}\widehat{\text {TL}}_{N}}(\textsf {W})\) and any increasing sequence  . This statement holds if and only if
. This statement holds if and only if  . Indeed, by Lemmas 4.8 and 5.6 we get
. Indeed, by Lemmas 4.8 and 5.6 we get

Therefore, we can write  for some polynomial
for some polynomial  . Note that this implies
. Note that this implies
What remains is to show that these polynomials only depend on the number of particles in  , in other words there exists \(p_k \in \mathbb {k}[q]\) so that
, in other words there exists \(p_k \in \mathbb {k}[q]\) so that  for all
for all  with
with  . Again it suffices to show this for two sequences
. Again it suffices to show this for two sequences  ,
,  of length k that differ in exactly one entry. So say \(i_s=i\), \(i_s^{\prime }=i+1\), and \(i_\ell =i_\ell ^{\prime }\) for all \(\ell \ne s\), for some \(1\le s\le k\) and \(i\in {\mathbb Z}/N{\mathbb Z}\). When \(1\le i\le N-1\),
of length k that differ in exactly one entry. So say \(i_s=i\), \(i_s^{\prime }=i+1\), and \(i_\ell =i_\ell ^{\prime }\) for all \(\ell \ne s\), for some \(1\le s\le k\) and \(i\in {\mathbb Z}/N{\mathbb Z}\). When \(1\le i\le N-1\),

and when \(i = 0\),

Hence we can write \(\varphi = \sum _{k=1}^{N-1} p_k \pi _k\) where \(\pi _k\) is the projection onto \(\mathbb {k}[q]\otimes \bigwedge ^k\mathbb {k}^N\), and we get that
where \(T_k\) denotes the multiplication action of the central element \(\mathbf t _k\), which is indeed a \(\text {n}\widehat{\text {TL}}_{N}\)-module endomorphism of \(\textsf {W}\). Thus, \( End _{\text {n}\widehat{\text {TL}}_{N}}(\textsf {W})\) is isomorphic to a direct sum of polynomial algebras as claimed. \(\square \)
Remark 5.8
The arguments in the proof of Proposition 5.7 remain valid even if we specialize the indeterminate q to some element in \(\mathbb {k}\setminus \{0\}\). In this case, we obtain that the summands \(\bigwedge ^k\mathbb {k}^N\) are simple modules and \( End _{\text {n}\widehat{\text {TL}}_{N}}\big (\bigoplus _{k=1}^{N-1}\bigwedge ^k\mathbb {k}^N\big )\ \cong \ \mathbb {k}^{N-1}\). For \(q=0\), the situation is more complicated: If q is specialized to zero, the generator \(a_0\) acts by zero on the module. The action of \(\text {n}\widehat{\text {TL}}_{N}\) factorizes over \( n TL _{N}\), and the module \(\bigwedge ^k\mathbb {k}^N\) is no longer simple. Instead it has a one-dimensional head spanned by the particle configuration \(v(1,\ldots ,k)\), and any endomorphism is given by choosing an image of this top configuration. It is always possible to map it to itself and to the one-dimensional socle spanned by \(v(N-k,\ldots ,N)\), but in general there are more endomorphisms. For example, in \(\bigwedge ^4\mathbb {k}^8\), the image of v(1, 2, 3, 4) may be any linear combination of v(1, 2, 3, 4), v(2, 3, 4, 8), v(3, 4, 7, 8), v(4, 6, 7, 8) and v(5, 6, 7, 8), so that \( End _{\text {n}\widehat{\text {TL}}_{8}}\Big (\bigwedge ^4\mathbb {k}^8\Big )\) is 5-dimensional.
6 The affine nilTemperley–Lieb algebra is finitely generated over its center
The affine nilTemperley–Lieb algebra is infinite dimensional when \(N \ge 3\); however, the following finiteness result holds:
Theorem 6.1
The algebra \(\text {n}\widehat{\text {TL}}_{N}\) is finitely generated over its center.
Proof
Given an arbitrary monomial  , we first factor it as
, we first factor it as  in the following way: Take the minimal particle configuration
in the following way: Take the minimal particle configuration  on which the monomial
on which the monomial  acts nontrivially; see Remark 4.3. The monomial
acts nontrivially; see Remark 4.3. The monomial  moves all of the particles by at least one step, because the particle configuration was assumed to be minimal. Using the faithfulness of the representation, we know that we may reorder the monomial
moves all of the particles by at least one step, because the particle configuration was assumed to be minimal. Using the faithfulness of the representation, we know that we may reorder the monomial  so that first each particle is moved one step clockwise, and afterwards the remaining particle moves are carried out. Hence, we may choose some factorization
so that first each particle is moved one step clockwise, and afterwards the remaining particle moves are carried out. Hence, we may choose some factorization  , where
, where  is a sequence obtained by permuting \(j_1, \ldots , j_k\) so that the particle at position \(j_r\) is moved one step clockwise by the action of \(a_{j_r}\) for all \(1\le r\le k\). The remaining particle moves are carried out by
is a sequence obtained by permuting \(j_1, \ldots , j_k\) so that the particle at position \(j_r\) is moved one step clockwise by the action of \(a_{j_r}\) for all \(1\le r\le k\). The remaining particle moves are carried out by  .
.
In Sect. 8, this decomposition is explicitly constructed (not using the faithful representation).
Next, we want to find an expression of the form

where \(a_\text {fin}\) is a monomial of some subalgebra \({}^i n TL _{N}\) of \(\text {n}\widehat{\text {TL}}_{N}\), \(\mathbf t _k^n\) is in the center of \(\text {n}\widehat{\text {TL}}_{N}\), and  is the above factor. Here
is the above factor. Here
denotes a copy of the finite nilTemperley–Lieb algebra \( n TL _{N}\) sitting in \(\text {n}\widehat{\text {TL}}_{N}\). To accomplish this, we have to subdivide the action of  on the particle configuration
on the particle configuration  one more time. There are two cases:
one more time. There are two cases:
-
1.
There is an index i not appearing in
 . In this case,
. In this case,  is an element of \({}^i n TL _{N}\) and we are done.
is an element of \({}^i n TL _{N}\) and we are done. -
2.
All indices appear at least \(n\ge 1\) times in
 . Let us investigate the action of
. Let us investigate the action of  on the particle configuration
on the particle configuration  , where
, where  . Note that
. Note that  is the minimal particle configuration for
is the minimal particle configuration for  . Each of the particles in
. Each of the particles in  is moved by
is moved by  to the position of the next particle in the sequence
to the position of the next particle in the sequence  , because there is no index missing (a missing index is equivalent to a particle being stopped before reaching the position of its successor), before possibly continuing to move along the circle. Again invoking the faithfulness of the representation, we can rewrite
, because there is no index missing (a missing index is equivalent to a particle being stopped before reaching the position of its successor), before possibly continuing to move along the circle. Again invoking the faithfulness of the representation, we can rewrite  , with the monomial
, with the monomial 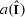 from Lemma 4.8. For maximal n, the remaining factor
from Lemma 4.8. For maximal n, the remaining factor  is an element of \({}^i n TL _{N}\) for some i. Observe that
is an element of \({}^i n TL _{N}\) for some i. Observe that  , which follows immediately from the definition of \(\mathbf t _k\) and Lemma 4.8.
, which follows immediately from the definition of \(\mathbf t _k\) and Lemma 4.8.
Therefore, we have shown that

where \(n =0\) in the first case. Since there are only finitely many monomials in \( {}^0 n TL _{N},{}^1 n TL _{N},\ldots ,{}^{N-1} n TL _{N}\) and only finitely many monomials  such that every index \(0,1,\ldots ,N-1\) occurs at most once in the sequence
such that every index \(0,1,\ldots ,N-1\) occurs at most once in the sequence  , the affine nilTemperley–Lieb algebra is indeed finitely generated over its center. \(\square \)
, the affine nilTemperley–Lieb algebra is indeed finitely generated over its center. \(\square \)
Remark 6.2
The affine nilTemperley–Lieb algebra is not free over its center (see [18]).
7 Embeddings of affine nilTemperley–Lieb algebras
In the proof of Theorem 6.1, we have used the N obvious embeddings of \( n TL _{N}\) into \(\text {n}\widehat{\text {TL}}_{N}\) coming from the N different embeddings of the Coxeter graph  into
into  . Next we construct N embeddings of \(\text {n}\widehat{\text {TL}}_{N}\) into \(\text {n}\widehat{\text {TL}}_{N+1}\). They correspond to the subdivision of an edge of
. Next we construct N embeddings of \(\text {n}\widehat{\text {TL}}_{N}\) into \(\text {n}\widehat{\text {TL}}_{N+1}\). They correspond to the subdivision of an edge of  by inserting a vertex on the edge to obtain
by inserting a vertex on the edge to obtain  .
.
Theorem 7.1
Let \(N\ge 3\). For any number \(0\le m \le N-1\), there is a unital embedding of algebras \(\varepsilon _m:\ \text {n}\widehat{\text {TL}}_{N}\ \rightarrow \ \text {n}\widehat{\text {TL}}_{N+1}\) given by
Lemma 7.2
For \(N \ge 3\), the map \(\varepsilon _m\) from \(\text {n}\widehat{\text {TL}}_{N}\) to \(\text {n}\widehat{\text {TL}}_{N+1}\) given by (3) is an algebra homomorphism.
Proof
Due to the circular nature of the relations, it suffices to check this for \(\varepsilon _0\). This amounts to showing the following, since all the other relations are readily apparent. To avoid confusion, we indicate generators of \(\text {n}\widehat{\text {TL}}_{N+1}\) in these calculations by \(\tilde{a}_i\):
Remark 7.3
How should one visualize the action of \(\varepsilon _m(\text {n}\widehat{\text {TL}}_{N}) \subset \text {n}\widehat{\text {TL}}_{N+1}\) on the particle configurations on a circle with \(N+1\) positions? Except for \(a_m\), all generators of \(\text {n}\widehat{\text {TL}}_{N}\) are mapped to corresponding generators of \(\text {n}\widehat{\text {TL}}_{N+1}\). They will act as before, by moving a particle one step clockwise around the circle. Since \(a_m\) is mapped by \(\varepsilon _m\) to the product \(\tilde{a}_{m+1}\tilde{a}_m\) in \(\text {n}\widehat{\text {TL}}_{N+1}\), it will move a particle from m to \(m+2\) as depicted in Fig. 5. In other words, the elements in \(\varepsilon _m(\text {n}\widehat{\text {TL}}_{N})\) do not move a particle to or from position \(m+1\).
Next we introduce a basis of \(\text {n}\widehat{\text {TL}}_{N}\) that will enable us to see directly that these homomorphisms are embeddings. The basis has a simple description in terms of the graphical representation \(\textsf {V}\) from Sect. 4. For any two particle configurations with \(1\le k\le N-1\) particles corresponding to the increasing sequences  and
and  , there is a monomial in \(\text {n}\widehat{\text {TL}}_{N}\) moving particles at the positions
, there is a monomial in \(\text {n}\widehat{\text {TL}}_{N}\) moving particles at the positions  to the positions
to the positions  . We require that every particle from
. We require that every particle from  be moved by at least one step, but we do not prescribe explicitly which of the j’s is mapped to which of the i’s. For
be moved by at least one step, but we do not prescribe explicitly which of the j’s is mapped to which of the i’s. For  , take
, take  to be the monomial such that the power of q in
to be the monomial such that the power of q in  is minimal (under the assumption that every particle from
is minimal (under the assumption that every particle from  must be moved). By faithfulness of the graphical representation,
must be moved). By faithfulness of the graphical representation,  is uniquely determined. For
is uniquely determined. For  , we have
, we have  , the special monomial defined in Sect. 4, hence
, the special monomial defined in Sect. 4, hence  Observe that one can write
Observe that one can write  , where the sum runs over all possible increasing sequences
, where the sum runs over all possible increasing sequences  of length k, and that
of length k, and that  is a monomial, since all but one summand vanish for
is a monomial, since all but one summand vanish for  .
.
Remark 7.4
The condition that  move all particles from
move all particles from  by at least one step guarantees that it acts as zero on all particle configurations with fewer particles than
by at least one step guarantees that it acts as zero on all particle configurations with fewer particles than  .
.
For example, when \(N=7\),
(Note that \(a_1\) moves v(0, 1) to v(0, 2), but this does not satisfy the requisite property that all the particles must be moved by at least one step.) If we apply the factorization of monomials from Theorem 6.1 to  , the minimality condition implies that
, the minimality condition implies that  , where if
, where if  , then
, then  is a sequence obtained by permuting the elements of
is a sequence obtained by permuting the elements of  .
.
Theorem 7.5
The set of monomials

defines a \(\mathbb {k}\)-basis of the affine nilTemperley–Lieb algebra \(\text {n}\widehat{\text {TL}}_{N}\).
Proof
First, observe that  is indeed a monomial since
is indeed a monomial since  . We show that the elements
. We show that the elements  act \(\mathbb {k}\)-linearly independently on the graphical representation \(\textsf {V}=\bigoplus _{k=0}^N \left( \mathbb {k}[q] \otimes \bigwedge ^k \mathbb {k}^N\right) \). By Remark 7.4, the monomial
act \(\mathbb {k}\)-linearly independently on the graphical representation \(\textsf {V}=\bigoplus _{k=0}^N \left( \mathbb {k}[q] \otimes \bigwedge ^k \mathbb {k}^N\right) \). By Remark 7.4, the monomial  acts by zero on summands \(\mathbb {k}[q] \otimes \bigwedge ^{k^{\prime }} \mathbb {k}^N\) for
acts by zero on summands \(\mathbb {k}[q] \otimes \bigwedge ^{k^{\prime }} \mathbb {k}^N\) for  . On
. On  , the matrix representing the action of
, the matrix representing the action of  relative to the standard basis has exactly one nonzero entry, and this one distinguishes all monomials with the same minimal number of particles
relative to the standard basis has exactly one nonzero entry, and this one distinguishes all monomials with the same minimal number of particles  . From these two observations, the linear independence follows. On the other hand, given any nonzero monomial in \(\text {n}\widehat{\text {TL}}_{N}\), there exists a minimal particle configuration
. From these two observations, the linear independence follows. On the other hand, given any nonzero monomial in \(\text {n}\widehat{\text {TL}}_{N}\), there exists a minimal particle configuration  on which it acts nontrivially. Recording the image particle configuration
on which it acts nontrivially. Recording the image particle configuration  and the power of q, we conclude that there is some \(\ell \) so that the element
and the power of q, we conclude that there is some \(\ell \) so that the element  acts on \(\textsf {V}\) in the same way as the given monomial does. Due to the faithfulness of this representation (see Theorem 4.5), the proposition follows. \(\square \)
acts on \(\textsf {V}\) in the same way as the given monomial does. Due to the faithfulness of this representation (see Theorem 4.5), the proposition follows. \(\square \)
In Sect. 8, a basis is constructed using a different approach (without relying on the faithful representation). Both bases are labelled by pairs of particle configurations (pairs of increasing sequences) together with a natural number \(\ell \). Up to an index shift in the output configuration  and a shift of the natural number \(\ell \), the labelling sets agree, and both bases actually coincide.
and a shift of the natural number \(\ell \), the labelling sets agree, and both bases actually coincide.
Proof
(Theorem 7.1) We have already proven in Lemma 7.2 that \(\varepsilon _m\) is an algebra homomorphism. Using Remark 7.3, observe that the monomial  is mapped to a monomial
is mapped to a monomial  (tilde again indicates in \(\text {n}\widehat{\text {TL}}_{N+1}\)), where the new index sets are obtained by \(i\mapsto i\) for \(0\le i\le m\) and \(i\mapsto {i+1}\) for \(m+1\le i\le N-1\). The injectivity follows since basis elements
(tilde again indicates in \(\text {n}\widehat{\text {TL}}_{N+1}\)), where the new index sets are obtained by \(i\mapsto i\) for \(0\le i\le m\) and \(i\mapsto {i+1}\) for \(m+1\le i\le N-1\). The injectivity follows since basis elements  of \(\text {n}\widehat{\text {TL}}_{N}\) are mapped to basis elements
of \(\text {n}\widehat{\text {TL}}_{N}\) are mapped to basis elements  of \(\text {n}\widehat{\text {TL}}_{N+1}\). \(\square \)
of \(\text {n}\widehat{\text {TL}}_{N+1}\). \(\square \)
Remark 7.6
It is possible to verify this theorem on generators and relations in the language of Sect. 8 without using the graphical description.
Remark 7.7
Observe that these embeddings work specifically for the affine nilTemperley–Lieb algebras but fail for the ordinary Temperley–Lieb algebras. The relation that fails to hold is the braid relation for Temperley–Lieb algebras, i.e. \(a_i a_{i\pm 1}a_i = a_i\). Interestingly, the relation \(a_i^2=\delta a_i\) is respected for \(\delta =1\).
8 A normal form and the faithfulness of the graphical representation
In this section, we prove Theorem 4.5 which we recall here:
Proposition
For \(N\ge 3\), \(\textsf {V}\) is a faithful \(\text {n}\widehat{\text {TL}}_{N}\)-module with respect to the action described in Definition 4.2.
For the proof, we will explicitly prove the linear independence of the matrices representing the monomials in \(\text {n}\widehat{\text {TL}}_{N}\). We proceed in three steps: (1) First, we define a normal form for the monomials. (2) Next, we find a bijection between the monomials and certain pairs of particle configurations together with a power of q. In other words, we find a basis for \(\text {n}\widehat{\text {TL}}_{N}\) and describe a labeling set. (3) The final step is the description of the action of a monomial on \(\textsf {V}\) using its matrix realization. The matrices representing the monomials have a distinguished nonzero entry that is given in terms of the particle configurations and the power of q from the bijection, and for most matrices, this is the only nonzero entry. From this description it will quickly follow that all these matrices are linearly independent.
8.1 Some useful facts
The following lemma characterises nonzero monomials in \(\text {n}\widehat{\text {TL}}_{N}\). They correspond to fully commutative elements in \(\widehat{ TL }_{N}\), see [9].
Lemma 8.1
The monomial  if and only if for any two neighbouring appearances of \(a_i\) in
if and only if for any two neighbouring appearances of \(a_i\) in  there are exactly one \(a_{i+1}\) and one \(a_{i-1}\) in between, apart from possible factors \(a_\ell \) for \(\ell \ne i-1,i,i+1\) (indices to be understood modulo N).
there are exactly one \(a_{i+1}\) and one \(a_{i-1}\) in between, apart from possible factors \(a_\ell \) for \(\ell \ne i-1,i,i+1\) (indices to be understood modulo N).
According to this result, two consecutive \(a_i\) have to enclose \(a_{i+1}\) and \(a_{i-1}\), i.e. \(a_i\ldots a_{i\pm 1}\ldots a_{i\mp 1}\ldots a_i\), with the dots being possible products of \(a_\ell \)’s with \(\ell \ne i\pm 1,i\). This lemma is a special case of [9, Lem. 2.6]; here is a quick proof for the convenience of the reader.
Proof
The monomial  is zero if and only if we can bring two neighbouring factors \(a_i\) together so that we obtain either \(a_i^2\) (‘square’) or \(a_ia_{i\pm 1}a_i\) (‘braid’). But expressions of the form \(a_i\ldots a_{i\pm 1}\ldots a_{i\mp 1}\ldots a_i\) cannot be resolved this way by commutativity relations. On the other hand, if there are two neighbouring factors \(a_i\) with either none or only one of the terms \(a_{i\pm 1}\) in between, we get after commutations either \(a_i^2\) or \(a_ia_{i\pm 1}a_i\). If there are at least two factors \(a_{i+1}\) (or \(a_{i-1}\)) in between the two \(a_i\), one can repeat the argument: Either we can create a square or a braid, or we have at least two factors of the same kind in between. In the case of a square or a braid we are done; otherwise we pick two neighbouring \(a_{i+k}\) in the kth step of the argument. Since we always consider the space in between two neighbouring factors \(a_i,a_{i+1},\ldots ,a_{i+k}\), none of the previous \(a_i,a_{i+1},\ldots ,a_{i+k-1}\) occurs between the two neighbouring \(a_{i+k}\). Unless we found a square or a braid in an earlier step, we end up in step \(N-1\) with a subexpression of the form \(a_{r}a_{r\pm 1}^ma_{r}\) which is zero for any \(m\ge 0\). \(\square \)
is zero if and only if we can bring two neighbouring factors \(a_i\) together so that we obtain either \(a_i^2\) (‘square’) or \(a_ia_{i\pm 1}a_i\) (‘braid’). But expressions of the form \(a_i\ldots a_{i\pm 1}\ldots a_{i\mp 1}\ldots a_i\) cannot be resolved this way by commutativity relations. On the other hand, if there are two neighbouring factors \(a_i\) with either none or only one of the terms \(a_{i\pm 1}\) in between, we get after commutations either \(a_i^2\) or \(a_ia_{i\pm 1}a_i\). If there are at least two factors \(a_{i+1}\) (or \(a_{i-1}\)) in between the two \(a_i\), one can repeat the argument: Either we can create a square or a braid, or we have at least two factors of the same kind in between. In the case of a square or a braid we are done; otherwise we pick two neighbouring \(a_{i+k}\) in the kth step of the argument. Since we always consider the space in between two neighbouring factors \(a_i,a_{i+1},\ldots ,a_{i+k}\), none of the previous \(a_i,a_{i+1},\ldots ,a_{i+k-1}\) occurs between the two neighbouring \(a_{i+k}\). Unless we found a square or a braid in an earlier step, we end up in step \(N-1\) with a subexpression of the form \(a_{r}a_{r\pm 1}^ma_{r}\) which is zero for any \(m\ge 0\). \(\square \)
Definition 8.2
For any \(i\in \{0,1,\ldots ,N-1\}\), we define a (clockwise) order \(\mathop {\prec }\limits ^{i}\) on the set \(\{0,1,\ldots ,N-1\}\) starting at i by
8.2 Step 1: A normal form
Given an arbitrary nonzero monomial  in \(\text {n}\widehat{\text {TL}}_{N}\), reorder its factors according to the following algorithm (as usual, the indices are considered modulo N):
in \(\text {n}\widehat{\text {TL}}_{N}\), reorder its factors according to the following algorithm (as usual, the indices are considered modulo N):
-
1.
Find all factors \(a_i\) in
 with no \(a_{i-1}\) to their right. We denote them by \(a_{i_1},\ldots ,a_{i_k}\), ordered according to their appearance in
with no \(a_{i-1}\) to their right. We denote them by \(a_{i_1},\ldots ,a_{i_k}\), ordered according to their appearance in  ; in other words,
; in other words,  is of the form
is of the form 
-
2.
Move the \(a_{i_1},\ldots ,a_{i_k}\) to the far right, without changing their internal order,

for
 and some sequence
and some sequence  . This is possible because
. This is possible because-
(a)
by assumption, there is no \(a_{i-1}\) to the right of an \(a_i\) in this list;
-
(b)
if for some i, \(a_{i+1}\) occurs to the right of some \(a_i\), then either \(a_i\ldots a_{i+1}\ldots a_i\) would occur as a subword without \(a_{i-1}\) in between, hence
 , or else \(a_{i+1}\) does not have \(a_i\) to its right, so it is one of the \(a_{i_1},\ldots ,a_{i_k}\) itself, and will be moved to the far right of
, or else \(a_{i+1}\) does not have \(a_i\) to its right, so it is one of the \(a_{i_1},\ldots ,a_{i_k}\) itself, and will be moved to the far right of  , too;
, too; -
(c)
\(a_i\) commutes with all \(a_\ell \) for \(\ell \ne i-1, i+1\).
-
(a)
-
3.
Repeat for
 until we get
until we get 
for sequences
 obtained successively the same way as described above. Notice:
obtained successively the same way as described above. Notice:-
Inside a sequence
 , every index occurs at most once. If two consecutive indices occur within
, every index occurs at most once. If two consecutive indices occur within  , they are increasingly ordered using the order \(\mathop {\prec }\limits ^{i_k}\) from Definition 8.2.
, they are increasingly ordered using the order \(\mathop {\prec }\limits ^{i_k}\) from Definition 8.2. -
For two consecutive sequences
 ,
,  and for every index \(i^{(n+1)}_r\) occurring in
and for every index \(i^{(n+1)}_r\) occurring in  , we can find some index \(i^{(n)}_s\) in
, we can find some index \(i^{(n)}_s\) in  such that \(i^{(n+1)}_r= i^{(n)}_{s}+1\).
such that \(i^{(n+1)}_r= i^{(n)}_{s}+1\). -
From that property, it also follows that the length of
 is less or equal than the length of
is less or equal than the length of  .
.
-
-
4.
Reorder the factors
 internally:
internally:-
(a)
Start with
 . There is some
. There is some  which does not occur in
which does not occur in  , but
, but  occurs. For example, this is satisfied by
occurs. For example, this is satisfied by  , as \(i_k\) occurs in
, as \(i_k\) occurs in  and is to the right of every other factor of
and is to the right of every other factor of  . Choose the largest such
. Choose the largest such  (with respect to the usual order). Then we can move
(with respect to the usual order). Then we can move  to the very right of the sequence
to the very right of the sequence  , because
, because  is not present, and
is not present, and  may only occur to the left of
may only occur to the left of  due to the construction of
due to the construction of  . We proceed in the same way with those indices
. We proceed in the same way with those indices  that appear in
that appear in  . The result is a reordering of the sequence
. The result is a reordering of the sequence  so that it is increasing from left to right with respect to
so that it is increasing from left to right with respect to  .
. -
(b)
Repeat with all other factors
 taking as the initial right-hand index of the sequence
taking as the initial right-hand index of the sequence  respectively, and reordering within each
respectively, and reordering within each  so that the indices are increasing from left to right with respect to
so that the indices are increasing from left to right with respect to  . Throughout, the index
. Throughout, the index  is the one from step (4a).
is the one from step (4a).
-
(a)
Example 8.3
As an example for \(\text {n}\widehat{\text {TL}}_{7}\), suppose  . (We omit the commas to simplify the notation.)
. (We omit the commas to simplify the notation.)
Find all \(a_i\) without \(a_{i-1}\) to their right: | \(a(6\ 4\ 2\ 1\ 3\ 5\ 4\ 2\ 0\ 6\ \underline{\underline{1}}\ 3\ \underline{\underline{2}}\ \underline{\underline{5}})\) |
Move them to the far right, and do not change their internal order: | \(a(6\ 4\ 2\ 1\ 3\ 5\ 4\ 2\ 0\ 6\ 3)\cdot a(1\ 2\ 5)\) |
Repeat: | \(a(6\ 4\ 2\ 3\ 5\ 4\ 1\ \underline{\underline{2}}\ 0\ \underline{\underline{6}}\ \underline{\underline{3}})\cdot a(1\ 2\ 5)\) |
\(a(6\ 4\ 2\ 3\ 5\ 4\ 1\ 0)\cdot a(2\ 6\ 3)\cdot a(1\ 2\ 5)\) | |
\(a(6\ 4\ 2\ \underline{\underline{3}}\ 5\ \underline{\underline{4}}\ 1\ \underline{\underline{0}})\cdot a(2\ 6\ 3)\cdot a(1\ 2\ 5)\) | |
\(a(6\ 4\ 2\ 5\ 1)\cdot a(3\ 4\ 0)\cdot a(2\ 6\ 3)\cdot a(1\ 2\ 5)\) | |
\(a(6\ \underline{4}\ 2\ \underline{\underline{5}}\ \underline{\underline{1}})\cdot a(3\ 4\ 0)\cdot a(2\ 6\ 3)\cdot a(1\ 2\ 5)\) | |
\(a(6\ 2)\cdot a(4\ 5\ 1)\cdot a(3\ 4\ 0)\cdot a(2\ 6\ 3)\cdot a(1\ 2\ 5)\) | |
With the right-hand indices of the | \(a(6\ 2)\cdot a(4\ 5\ 1)\cdot a(3\ 4\ 0)\cdot a(2\ 3\ 6)\cdot a(1\ 2\ 5)\) |
As a shorthand notation, in the following we often identify the index sequence  with
with  (and manipulate
(and manipulate  according to the same relations as
according to the same relations as  ) as demonstrated in the following example.
) as demonstrated in the following example.
Example 8.4
Let \(N=6\).

Lemma 8.5
Let  be a nonzero monomial in \(\text {n}\widehat{\text {TL}}_{N}\), where we use as always the notation from Section 2. Let
be a nonzero monomial in \(\text {n}\widehat{\text {TL}}_{N}\), where we use as always the notation from Section 2. Let  be the monomials constructed by the algorithm above.
be the monomials constructed by the algorithm above.
-
1.
The equality
 holds in \(\text {n}\widehat{\text {TL}}_{N}\).
holds in \(\text {n}\widehat{\text {TL}}_{N}\). -
2.
Given any two representatives
 ,
, 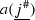 of the same element in \(\text {n}\widehat{\text {TL}}_{N}\), the above algorithm creates the same representative
of the same element in \(\text {n}\widehat{\text {TL}}_{N}\), the above algorithm creates the same representative 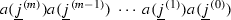 for both
for both  and
and  .
.
Proof
-
1.
The algorithm never interchanges the order of two factors \(a_i\), \(a_{i\pm 1}\) with consecutive indices within
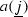 . Hence, the reordering of the factors of
. Hence, the reordering of the factors of  uses only the commutativity relation \(a_i a_j = a_j a_i\) for \(i-j \ne \pm 1\text { mod }N\) of \(\text {n}\widehat{\text {TL}}_{N}\).
uses only the commutativity relation \(a_i a_j = a_j a_i\) for \(i-j \ne \pm 1\text { mod }N\) of \(\text {n}\widehat{\text {TL}}_{N}\). -
2.
Two monomials
 ,
,  in \(\text {n}\widehat{\text {TL}}_{N}\) are equal if and only if they only differ by applications of commutativity relations \(a_i a_j = a_j a_i\) for \(i-j \ne \pm 1\text { mod }N\), hence, if and only if they contain the same number of factors \(a_i\) for each i and the relative position of each \(a_i\) and \(a_{i\pm 1}\) is the same. Since the outcome of the algorithm depends only on the relative positions of consecutive indices, the resulting decomposition
in \(\text {n}\widehat{\text {TL}}_{N}\) are equal if and only if they only differ by applications of commutativity relations \(a_i a_j = a_j a_i\) for \(i-j \ne \pm 1\text { mod }N\), hence, if and only if they contain the same number of factors \(a_i\) for each i and the relative position of each \(a_i\) and \(a_{i\pm 1}\) is the same. Since the outcome of the algorithm depends only on the relative positions of consecutive indices, the resulting decomposition 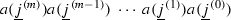 is the same.
is the same.
\(\square \)
We have shown the following. In stating this result and subsequently, whenever we refer to monomials in normal form, we assume the monomial is nonzero and nonconstant, in particular the sequence  is nonempty.
is nonempty.
Theorem 8.6
Assume \(N \ge 3\).
-
1.
The algorithm in Step 1 above provides a normal form for nonzero monomials
 in the generators \(a_i\) of \(\text {n}\widehat{\text {TL}}_{N}\), or equivalently for nonzero fully commutative monomials in \(\widehat{ TL }_{N}\), so that
in the generators \(a_i\) of \(\text {n}\widehat{\text {TL}}_{N}\), or equivalently for nonzero fully commutative monomials in \(\widehat{ TL }_{N}\), so that 
where \(a^{(n)}_{i_\ell }\in \{1,a_0,a_1,\ldots ,a_{N-1}\}\text { for all }1\le n\le m,\ 1\le \ell \le k\), and
$$\begin{aligned} a^{(n+1)}_{i_\ell }\in {\left\{ \begin{array}{ll}\{1\} &{}\quad \text {if }a^{(n)}_{i_\ell }=1,\\ \{1,a_{j+1}\} &{}\quad \text {if }a^{(n)}_{i_\ell }=a_j.\end{array}\right. } \end{aligned}$$The factors \(a_{i_1},\ldots ,a_{i_k}\) are determined by the property that the generator \(a_{i_\ell -1}\) does not appear to the right of \(a_{i_\ell }\) in the original presentation of the monomial. The internal ordering of the factors is increasing with respect to the relation
 , as in Step (4a) of the normal form algorithm, where
, as in Step (4a) of the normal form algorithm, where  is the largest value in \(\{0,1,\ldots , N-1\}\) such that
is the largest value in \(\{0,1,\ldots , N-1\}\) such that  , but
, but 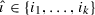 .
. -
2.
The set
 is a \(\mathbb {k}\)-basis of \(\text {n}\widehat{\text {TL}}_{N}\).
is a \(\mathbb {k}\)-basis of \(\text {n}\widehat{\text {TL}}_{N}\).
8.3 Step 2: Labelling of basis elements
Definition 8.7
Given  in normal form, we call
in normal form, we call  the \(\ell \)th block of
the \(\ell \)th block of  , and a string of indices of maximal length of the form
, and a string of indices of maximal length of the form  (modulo N) the sth strand of
(modulo N) the sth strand of  . We use the notation \([\ldots ,i_s+1,i_s]\) for the strands.
. We use the notation \([\ldots ,i_s+1,i_s]\) for the strands.
Example 8.8
Let \(N=6\), and consider Example 8.4 once again, where

The blocks are  ,
,  ,
,  ,
,  ,
,  , and
, and  . The strands are [3210], [54321], [105432] and [21054]. In particular, strands (and blocks) can have different lengths, but the longest strand has length \(m=6\).
. The strands are [3210], [54321], [105432] and [21054]. In particular, strands (and blocks) can have different lengths, but the longest strand has length \(m=6\).
Each monomial  determines two sets
determines two sets  and an integer
and an integer  as follows:
as follows:

These are well defined because, as in the proof of Lemma 8.5, any element of \(\text {n}\widehat{\text {TL}}_{N}\) is uniquely determined by the number of factors \(a_i\) and the relative position of each \(a_i\) and \(a_{i\pm 1}\), for all i. The set  equals the underlying set of
equals the underlying set of  in the normal form from the algorithm above. All strands of
in the normal form from the algorithm above. All strands of  begin with an element in
begin with an element in  and end with an element from
and end with an element from  .
.
The goal of this subsection is to show
Proposition 8.9
The mapping

is injective, where \(\mathcal{P}_N\) is the power set of \(\{0,1,\ldots ,N-1\}\).
Remark 8.10
The map \(\psi \) is defined so that in the graphical description of the representation \(\textsf {V}\) of \(\text {n}\widehat{\text {TL}}_{N}\), the set  equals the set of positions where
equals the set of positions where  expects a particle to be. The set
expects a particle to be. The set  equals the set of positions where
equals the set of positions where  moves the particles from
moves the particles from  , but each one is translated by 1, that is,
, but each one is translated by 1, that is,

The map \(\psi \) is far from being surjective. An obvious constraint is that  , and furthermore, for some pairs
, and furthermore, for some pairs  , one can only obtain sufficiently large values
, one can only obtain sufficiently large values  .
.
To ease the presentation, we start by proving injectivity of the restriction \(\psi _0\) of \(\psi \) to those monomials  in normal form whose first element \(i_1\) of
in normal form whose first element \(i_1\) of  is 0. The proof itself will amount to counting indices.
is 0. The proof itself will amount to counting indices.
Proposition 8.11
The map

is injective.
Before beginning the proof of this result, we note that for monomials  with \(i_1=0\), the inequality \(i_k<N-1\) must hold in
with \(i_1=0\), the inequality \(i_k<N-1\) must hold in  , since \(i_1 = 0\) implies that \(i_1-1=N-1\) is not an element of
, since \(i_1 = 0\) implies that \(i_1-1=N-1\) is not an element of  . Consequently, the ordering of the indices in
. Consequently, the ordering of the indices in  agrees with the natural ordering of \({\mathbb Z}\), so we can regard
agrees with the natural ordering of \({\mathbb Z}\), so we can regard  as a subset of \(({\mathbb Z},<)\) and replace the modular index sequence
as a subset of \(({\mathbb Z},<)\) and replace the modular index sequence  by an integral index sequence
by an integral index sequence  such that
such that  as follows:
as follows:
Definition 8.12
Assume  is a normal form sequence with
is a normal form sequence with  and
and  , where indices in
, where indices in  are modulo N and \(1\le k(n)\le k\) for all \(1\le n\le m\). The integral normal form sequence for
are modulo N and \(1\le k(n)\le k\) for all \(1\le n\le m\). The integral normal form sequence for
 is
is

for \(n = 1,\dots ,m\).
Example 8.13
We continue Example 8.4 with \(N=6\).

Our proof of Proposition 8.11 will hinge upon the following technical lemma.
Lemma 8.14
Let  be the integral normal form sequence for
be the integral normal form sequence for  and let \([i_s,\ldots , i_s+n_s]\) for \(s=1,\dots ,k\) be the strands of
and let \([i_s,\ldots , i_s+n_s]\) for \(s=1,\dots ,k\) be the strands of  . Assume \(i_1 = 0\). Then
. Assume \(i_1 = 0\). Then
-
(a)
\(n_1 =i_1+n_1< i_2+n_2< \cdots < i_k+n_k;\)
-
(b)
\(i_k+n_k< i_1+n_1+N = n_1+N\).
We postpone the proof of this result and proceed directly to proving the proposition.
Proof
(Proposition 8.11) Since the sequence  will be fixed throughout the proof, we will drop the subscript
will be fixed throughout the proof, we will drop the subscript  on
on  . To show the injectivity of \(\psi _0\), we consider the factorization \(\psi _0=\gamma \circ \beta \circ \alpha \) given by
. To show the injectivity of \(\psi _0\), we consider the factorization \(\psi _0=\gamma \circ \beta \circ \alpha \) given by

where  and
and  similar to the definition of
similar to the definition of  . The map \(\alpha \) replaces indices in \({\mathbb Z}/N{\mathbb Z}\) by indices in \({\mathbb Z}\) as in Definition 8.12 above. The map \(\beta \) is given by reading off
. The map \(\alpha \) replaces indices in \({\mathbb Z}/N{\mathbb Z}\) by indices in \({\mathbb Z}\) as in Definition 8.12 above. The map \(\beta \) is given by reading off  and
and  from
from  . The map \(\gamma \) sends the pair
. The map \(\gamma \) sends the pair  to a triple consisting of the respective images
to a triple consisting of the respective images  modulo N of the pair and the integer \(\ell =1+\sum \ell _r\) where \(\ell _r=\lfloor \frac{j_r}{N}\rfloor \) for each
modulo N of the pair and the integer \(\ell =1+\sum \ell _r\) where \(\ell _r=\lfloor \frac{j_r}{N}\rfloor \) for each  . The summand 1 corresponds to \(0=i_1\); all other occurrences of 0 are counted by \(\sum \ell _r\). Now we check injectivity.
. The summand 1 corresponds to \(0=i_1\); all other occurrences of 0 are counted by \(\sum \ell _r\). Now we check injectivity.
The map \(\alpha \) is clearly injective since  is a left inverse map.
is a left inverse map.
To see that \(\beta \) is injective, we need to know that  can be uniquely reconstructed from
can be uniquely reconstructed from  . Observe that
. Observe that  is determined by knowing all the ‘strands’ \(i_s, i_s+1, i_s+2,\ldots , i_s+n_s\) for \(1\le s\le k\), hence by assigning an element
is determined by knowing all the ‘strands’ \(i_s, i_s+1, i_s+2,\ldots , i_s+n_s\) for \(1\le s\le k\), hence by assigning an element  to each
to each  . But it follows from Lemma 8.14 (a) that \(i_1+n_1\) must be the smallest element of
. But it follows from Lemma 8.14 (a) that \(i_1+n_1\) must be the smallest element of  , \(i_2+n_2\) the second smallest, etc., so that the element \(i_s+n_s\) is assigned to the sth element in
, \(i_2+n_2\) the second smallest, etc., so that the element \(i_s+n_s\) is assigned to the sth element in  , that is, to \(i_s\).
, that is, to \(i_s\).
Now to see that \(\gamma \) is injective, we need to recover  in a unique way from
in a unique way from  . Write
. Write  , and set
, and set  . By Lemma 8.14 (a), we know that
. By Lemma 8.14 (a), we know that  is of the form \((i_1+n_1<\cdots <i_k+n_k)\), and since the elements of
is of the form \((i_1+n_1<\cdots <i_k+n_k)\), and since the elements of  have to be equal to the elements of
have to be equal to the elements of  modulo N, we can write \(i_r+n_r=N\ell _r+d_r\) for \(\ell _r=\lfloor \frac{i_r+n_r}{N}\rfloor \) and some
modulo N, we can write \(i_r+n_r=N\ell _r+d_r\) for \(\ell _r=\lfloor \frac{i_r+n_r}{N}\rfloor \) and some  . Comparing \(\ell _r\) and \(\ell _s\) for \(r<s\), we have
. Comparing \(\ell _r\) and \(\ell _s\) for \(r<s\), we have
So \(\ell _r< \ell _s+1\), i.e. \(\ell _r\le \ell _s\). Similarly, we obtain from (b) of Lemma 8.14 that \(\ell _k\le \ell _1+1\).
As a result,
i.e. \(\ell _k<\ell _1+2\). Together we have \(\ell _1=\cdots =\ell _s <\ell _{s+1}=\cdots =\ell _1+1\) for some \(1<s\le k\) (where we treat the case \(s=k\) by \(\ell _1=\cdots =\ell _k\)). Set \(\tilde{\ell }{:=}\ell _1\). Then
As a first consequence,
which determines \(\tilde{\ell }= \lfloor \frac{\ell -1}{k}\rfloor \), and hence all \(\ell _r\), as well as the index s. Using Lemma 8.14, we determine that
and so
Therefore, \(d_{s+1}<\cdots<d_k<d_1<\cdots <d_s\), which fixes the choice of \(d_r\) for all r. We conclude that given  , we can reconstruct
, we can reconstruct  by setting \(i_r+n_r{:=}N\, \ell _r+d_r\). This completes the proof of Proposition 8.11. \(\square \)
by setting \(i_r+n_r{:=}N\, \ell _r+d_r\). This completes the proof of Proposition 8.11. \(\square \)
Proof
(Lemma 8.14) (a) Let  be a nonempty integral normal form sequence with \(0=i_1<\cdots <i_k\le N-1\) and strands \([i_r,\ldots ,i_r+n_r]\) for \(1\le r\le k\). Assume that there is some index \(1\le t\le k-1\) such that \(i_t+n_t\ \ge \ i_{t+1}+n_{t+1}\). Since \(i_t<i_{t+1}\), we have \(n_t> n_{t+1}\). So
be a nonempty integral normal form sequence with \(0=i_1<\cdots <i_k\le N-1\) and strands \([i_r,\ldots ,i_r+n_r]\) for \(1\le r\le k\). Assume that there is some index \(1\le t\le k-1\) such that \(i_t+n_t\ \ge \ i_{t+1}+n_{t+1}\). Since \(i_t<i_{t+1}\), we have \(n_t> n_{t+1}\). So

From \(i_t +n_{t+1}\ <\ i_{t+1}+n_{t+1}\ \le \ i_t+n_t\) it follows that there is some integer \(n_{t+1}<p\le n_t\) such that \(i_{t+1}+n_{t+1}=i_t+p\) appears in the strand \([i_t,\ldots ,i_t+n_t]\), i.e.

with \(i_t+p=i_{t+1}+n_{t+1}\). But by the definition of the strands, there is no \(i_{t+1}+n_{t+1}+1\) appearing to the left of \(i_{t+1}+n_{t+1}\). Due to Lemma 8.1, we know that (even modulo N) there is no repetition of \(i_{t+1}+n_{t+1}\) to the left. Thus \(i_t+p=i_{t+1}+n_{t+1}\) is not possible, and we obtain \(i_1+n_1< i_2+n_2< \cdots < i_k+n_k\).
For (b) of Lemma 8.14, assume \(i_k+n_k\ge i_1+n_1+N\). It is true generally that \(N>i_k\), so we get \(i_k+n_k \ge i_1+n_1+N>i_k+n_1\). Hence \(i_1+n_1+N=i_k+b\) for some \(n_1<b\le n_k\), i.e. \(i_1+n_1+N\) appears in the strand \([i_k,\ldots , i_k+n_k]\) and we have

Here it may be that the \(n_k\)th bracket and the bth bracket coincide, but in any case, we find that \(i_k+b\ =\ i_1+n_1+N\ = \ i_1+n_1\text { mod } N\), and so \(i_k+b\) appears to the left of \(i_1+n_1\). By the definition of the strands, there is no \(i_1+n_1+1\) to the left of \(i_1+n_1\), and from Lemma 8.1 we deduce that in  there is no \(i_1+n_1\text { mod }N\) to the left of \(i_1+n_1\) allowed, which leads to a contradiction. Hence \(i_k+n_k < i_1+n_1+N\) must hold. \(\square \)
there is no \(i_1+n_1\text { mod }N\) to the left of \(i_1+n_1\) allowed, which leads to a contradiction. Hence \(i_k+n_k < i_1+n_1+N\) must hold. \(\square \)
Having established that \(\psi \) is injective when restricted to sequences with \(i_1 = 0\), we now show the injectivity of \(\psi \) in general.
Proof
(Proposition 8.9) We have the following disjoint decompositions according to the smallest value \(i_1\) in  :
:

By Proposition 8.11, the map  restricted to those
restricted to those  with \(i_1=0\) is injective. We argue next that by an index shift this result is true for all other \(\psi _i\).
with \(i_1=0\) is injective. We argue next that by an index shift this result is true for all other \(\psi _i\).
Now it follows from Proposition 8.11 that the map

is injective, where  counts the occurences of \(N-i\) in
counts the occurences of \(N-i\) in  . Recall that
. Recall that

Now observe that we can obtain  from
from  as
as

which follows from a computation using  and
and
We obtain \(\psi _i\) by first shifting the indices of  by subtracting i from each index,
by subtracting i from each index,  , then applying \(\widehat{\psi }_0\), and finally shifting the indices from
, then applying \(\widehat{\psi }_0\), and finally shifting the indices from  and
and  by adding i to each. Hence, \(\psi _i\) is injective for each i, and \(\psi \) is injective because the unions are disjoint. \(\square \)
by adding i to each. Hence, \(\psi _i\) is injective for each i, and \(\psi \) is injective because the unions are disjoint. \(\square \)
8.4 Step 3: Description and linear independence of the matrices
Recall that the standard \(\mathbb {k}\)-basis of the representation \(\textsf {V}=\bigoplus _{k=0}^N\left( \mathbb {k}[q] \otimes \bigwedge ^k\mathbb {k}^N\right) \) is given by
where \((i_1,\ldots ,i_k)\) is identified with the particle configuration having particles in those positions in the graphical description. Now we describe with respect to this basis the matrix representing a nonzero monomial  as a \(2^N\times 2^N\)-matrix with entries in \(\mathbb {k}[q]\). Since \(\textsf {V}\) decomposes as a \(\text {n}\widehat{\text {TL}}_{N}\)-module into submodules \(\mathbb {k}[q] \otimes \bigwedge ^k\mathbb {k}^N\) for \(k = 0,1,\ldots , N\), the matrix of
as a \(2^N\times 2^N\)-matrix with entries in \(\mathbb {k}[q]\). Since \(\textsf {V}\) decomposes as a \(\text {n}\widehat{\text {TL}}_{N}\)-module into submodules \(\mathbb {k}[q] \otimes \bigwedge ^k\mathbb {k}^N\) for \(k = 0,1,\ldots , N\), the matrix of  is block diagonal with \(N+1\) blocks \(A_0,A_1,\ldots ,A_N\), where \(A_0=A_N=(0)\) corresponding to the trivial representation.
is block diagonal with \(N+1\) blocks \(A_0,A_1,\ldots ,A_N\), where \(A_0=A_N=(0)\) corresponding to the trivial representation.

The block \(A_k\) is a \(\left( {\begin{array}{c}N\\ k\end{array}}\right) \times \left( {\begin{array}{c}N\\ k\end{array}}\right) \)-matrix, with entries from \(\mathbb {k}[q]\) indexed by all possible particle configurations whose number of particles equal to k.
Now fix a nonzero monomial  in normal form that is specified by the triple
in normal form that is specified by the triple  defined in Step 2. Let
defined in Step 2. Let  . All blocks \(A_1,\ldots ,A_{k-1}\) are zero since
. All blocks \(A_1,\ldots ,A_{k-1}\) are zero since  expects at least k particles. For \(r>k\) there might be nonzero blocks \(A_r\). Such nonzero blocks appear unless the particles from
expects at least k particles. For \(r>k\) there might be nonzero blocks \(A_r\). Such nonzero blocks appear unless the particles from  are moved around the whole circle with no position left out, in which case there are no surplus particles allowed. This occurs if
are moved around the whole circle with no position left out, in which case there are no surplus particles allowed. This occurs if  contains at least every other generator \(a_i,a_{i+2},\ldots \).
contains at least every other generator \(a_i,a_{i+2},\ldots \).
More importantly, the block \(A_k\) has precisely one nonzero entry, and this is given by

From this we see first that all matrices representing monomials  in normal form with
in normal form with  are \(\mathbb {k}\)-linearly independent: They have only one nonzero entry which is equal to
are \(\mathbb {k}\)-linearly independent: They have only one nonzero entry which is equal to  at position
at position  . Furthermore, if all matrices representing monomials
. Furthermore, if all matrices representing monomials  in normal form with
in normal form with  are \(\mathbb {k}\)-linearly independent, then also all matrices representing monomials
are \(\mathbb {k}\)-linearly independent, then also all matrices representing monomials  in normal form with
in normal form with  are \(\mathbb {k}\)-linearly independent. This follows because the additional monomials
are \(\mathbb {k}\)-linearly independent. This follows because the additional monomials  with
with  have nonzero entries
have nonzero entries  in the \((k-1)\)th block which is zero for all
in the \((k-1)\)th block which is zero for all  with
with  . So by induction, all matrices representing monomials
. So by induction, all matrices representing monomials  in normal form are \(\mathbb {k}\)-linearly independent. Since all of them have a zero entry in the upper left (and lower right) corner, we may add the identity matrix to the linearly independent set of matrices, and it remains linearly independent. So the representation of \(\text {n}\widehat{\text {TL}}_{N}\) on \(\textsf {V}\) is faithful, because according to Theorem 8.6,
in normal form are \(\mathbb {k}\)-linearly independent. Since all of them have a zero entry in the upper left (and lower right) corner, we may add the identity matrix to the linearly independent set of matrices, and it remains linearly independent. So the representation of \(\text {n}\widehat{\text {TL}}_{N}\) on \(\textsf {V}\) is faithful, because according to Theorem 8.6,  is a \(\mathbb {k}\)-basis of
is a \(\mathbb {k}\)-basis of  .
.
Section 8 has given a normal form for each monomial and has provided an alternate proof of the faithfulness of the representation of  by elementary arguments.
by elementary arguments.
References
Alharbat, S.: A classification of affine fully commutative elements. arXiv:1311.7089
Berenstein, A., Fomin, S., Zelevinsky, A.: Parametrizations of canonical bases and totally positive matrices. Adv. Math. 122(1), 49–149 (1996)
Bernštein, I.N., Gel’fand, I.M., Gel’fand, S.I.: Schubert cells, and the cohomology of the spaces \(G/P\). Uspehi Mat. Nauk 28(3), 3–26 (1973)
Billey, S.C., Jockusch, W., Stanley, R.P.: Some combinatorial properties of Schubert polynomials. J. Algebraic Comb. 2(4), 345–374 (1993)
Brichard, J.: On Using Graphical Calculi: Centers, Zeroth Hochschild Homology and Possible Compositions of Induction and Restriction Functors in Various Diagrammatical Algebras. Thesis (Ph.D.), Columbia University, ProQuest LLC (2011)
Crane, L., Frenkel, I.B.: Four-dimensional topological quantum field theory, Hopf categories, and the canonical bases. Topology and physics. J. Math. Phys. 35(10), 5136–5154 (1994)
Fan, C.K., Green, R.M.: On the affine Temperley–Lieb algebras. J. Lond. Math. Soc. (2) 60(2), 366–380 (1999)
Fomin, S., Stanley, R.P.: Schubert polynomials and the nil-Coxeter algebra. Adv. Math. 103(2), 196–207 (1994)
Green, R.M.: On 321-avoiding permutations in affine Weyl groups. J. Algebraic Comb. 15(3), 241–252 (2002)
Khovanov, M.: Nilcoxeter algebras categorify the Weyl algebra. Commun. Algebra 29(11), 5033–5052 (2001)
Kostant, B., Kumar, S.: The nil Hecke ring and cohomology of \(G/P\) for a Kac-Moody group \(G\). Adv. Math. 62(3), 187–237 (1986)
Korff, C., Stroppel, C.: The \(\widehat{{\mathfrak{sl}}}(n)_k\)-WZNW fusion ring: a combinatorial construction and a realisation as quotient of quantum cohomology. Adv. Math. 225(1), 200–268 (2010)
Koenig, S., Xi, C.: Affine cellular algebras. Adv. Math. 229(1), 139–182 (2012)
Lam, T.: Affine Stanley symmetric functions. Am. J. Math. 128(6), 1553–1586 (2006)
Lam, T.: Schubert polynomials for the affine Grassmannian. J. Am. Math. Soc. 21(1), 259–281 (2008)
Lascoux, A., Schützenberger, M.-P.: Fonctorialité des polynômes de Schubert. Invariant theory (Denton, TX, 1986), Contemp. Math., vol. 88, Am. Math. Soc. Providence, RI, pp. 585–598 (1989)
Macdonald, I.G., Schubert polynomials. Surveys in combinatorics, 1991 (Guildford, 1991), London Math. Soc. Lecture Note Ser., vol. 166, Cambridge Univ. Press, Cambridge, pp. 73–99 (1991)
Meinel, J.: Affine nilTemperley–Lieb Algebras and Generalized Weyl Algebras: Combinatorics and Representation Theory. Dissertation, Bonn (2016)
Postnikov, A.: Affine approach to quantum Schubert calculus. Duke Math. J. 128(3), 473–509 (2005)
Ridout, D., Saint-Aubin, Y.: Standard modules, induction and the Temperley–Lieb algebra. Adv. Theor. Math. Phys. 18(5), 957–1041 (2014)
Acknowledgments
Open access funding provided by Max Planck Society Max Planck Institute for Mathematics.
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors thank Catharina Stroppel for many helpful discussions and express their gratitude to the Mathematical Sciences Research Institute (MSRI) where their joint research began. The authors thank the referee for very detailed remarks. The second author would like to thank Daniel Tubbenhauer for remarks on the embeddings. This work is part of the second author’s Ph.D. project at the MPIM Bonn, supported by a grant of the Deutsche Telekom Stiftung.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Benkart, G., Meinel, J. The center of the affine nilTemperley–Lieb algebra. Math. Z. 284, 413–439 (2016). https://doi.org/10.1007/s00209-016-1660-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-016-1660-7



 .
. has generators
has generators 



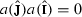 for all
for all  we get
we get  . In this case,
. In this case,  is an element of
is an element of  . Let us investigate the action of
. Let us investigate the action of  on the particle configuration
on the particle configuration  , where
, where  . Note that
. Note that  is the minimal particle configuration for
is the minimal particle configuration for  . Each of the particles in
. Each of the particles in  is moved by
is moved by  to the position of the next particle in the sequence
to the position of the next particle in the sequence  , because there is no index missing (a missing index is equivalent to a particle being stopped before reaching the position of its successor), before possibly continuing to move along the circle. Again invoking the faithfulness of the representation, we can rewrite
, because there is no index missing (a missing index is equivalent to a particle being stopped before reaching the position of its successor), before possibly continuing to move along the circle. Again invoking the faithfulness of the representation, we can rewrite  , with the monomial
, with the monomial 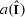 from Lemma
from Lemma  is an element of
is an element of  , which follows immediately from the definition of
, which follows immediately from the definition of 
 with no
with no  ; in other words,
; in other words,  is of the form
is of the form 

 and some sequence
and some sequence  . This is possible because
. This is possible because , or else
, or else  , too;
, too; until we get
until we get 
 obtained successively the same way as described above. Notice:
obtained successively the same way as described above. Notice: , every index occurs at most once. If two consecutive indices occur within
, every index occurs at most once. If two consecutive indices occur within  , they are increasingly ordered using the order
, they are increasingly ordered using the order  ,
,  and for every index
and for every index  , we can find some index
, we can find some index  such that
such that  is less or equal than the length of
is less or equal than the length of  .
. internally:
internally: . There is some
. There is some  which does not occur in
which does not occur in  , but
, but  occurs. For example, this is satisfied by
occurs. For example, this is satisfied by  , as
, as  and is to the right of every other factor of
and is to the right of every other factor of  . Choose the largest such
. Choose the largest such  (with respect to the usual order). Then we can move
(with respect to the usual order). Then we can move  to the very right of the sequence
to the very right of the sequence  , because
, because  is not present, and
is not present, and  may only occur to the left of
may only occur to the left of  due to the construction of
due to the construction of  . We proceed in the same way with those indices
. We proceed in the same way with those indices  that appear in
that appear in  . The result is a reordering of the sequence
. The result is a reordering of the sequence  so that it is increasing from left to right with respect to
so that it is increasing from left to right with respect to  .
. taking as the initial right-hand index of the sequence
taking as the initial right-hand index of the sequence  respectively, and reordering within each
respectively, and reordering within each  so that the indices are increasing from left to right with respect to
so that the indices are increasing from left to right with respect to  . Throughout, the index
. Throughout, the index  is the one from step (4a).
is the one from step (4a). ,
,  from left to right, reorder the factors in each
from left to right, reorder the factors in each  increasingly with respect to
increasingly with respect to  from left to right:
from left to right: holds in
holds in  ,
, 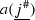 of the same element in
of the same element in 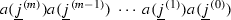 for both
for both  and
and  .
.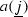 . Hence, the reordering of the factors of
. Hence, the reordering of the factors of  uses only the commutativity relation
uses only the commutativity relation  ,
,  in
in 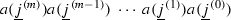 is the same.
is the same. in the generators
in the generators 
 , as in Step (4a) of the normal form algorithm, where
, as in Step (4a) of the normal form algorithm, where  is the largest value in
is the largest value in  , but
, but 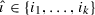 .
. is a
is a