Skip to main content
SpringerLink
Log in

Combined effects of two nonlinearities in lifespan of small solutions to semi-linear wave equations

  • Published:
Mathematische Annalen Aims and scope Submit manuscript

Abstract

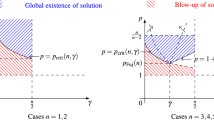
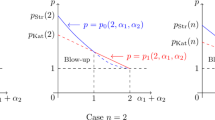
This paper investigates the combined effects of two distinctive power-type nonlinear terms (with parameters \(p,q>1\)) in the lifespan of small solutions to semi-linear wave equations. We determine the full region of (p, q) to admit global existence of small solutions, at least for spatial dimensions \(n=2, 3\). Moreover, for many (p, q) when there is no global existence, we obtain sharp lower bound of the lifespan, which is of the same order as the upper bound of the lifespan.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Agemi, R.: Blow-up of solutions to nonlinear wave equations in two space dimensions. Manuscripta Math. 73, 153–162 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  2. Bergh, J., Löfström, J.: Interpolation spaces. An introduction. In: Grundlehren der Mathematischen Wissenschaften, vol. 223. Springer, Berlin (1976)

  3. Fang, D., Wang, C.: Weighted Strichartz estimates with angular regularity and their applications. Forum Math. 23, 181–205 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  4. Georgiev, V., Lindblad, H., Sogge, C.D.: Weighted Strichartz estimates and global existence for semilinear wave equations. Am. J. Math. 119, 1291–1319 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  5. Glassey, R.T.: Finite-time blow-up for solutions of nonlinear wave equations. Math. Z. 177, 323–340 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  6. Glassey, R.T.: Existence in the large for \(\Box u=F(u)\) in two space dimensions. Math. Z. 178, 233–261 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  7. Han, W., Zhou, Y.: Blow up for some semilinear wave equations in multi-space dimensions. Commun. Partial Differ. Equ. 39, 651–665 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  8. Hidano, K.: Small data scattering for wave equations with super critical nonlinearity. In: Proceedings of the 23rd Sapporo Symposium on Partial Differential Equations (Yoshikazu Giga, Edt.), pp. 23–30 (1998). http://eprints3.math.sci.hokudai.ac.jp/1232/1/53

  9. Hidano, K., Metcalfe, J., Smith, H.F., Sogge, C.D., Zhou, Y.: On abstract Strichartz estimates and the Strauss conjecture for nontrapping obstacles. Trans. Am. Math. Soc. 362, 2789–2809 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hidano, K., Tsutaya, K.: Global existence and asymptotic behavior of solutions for nonlinear wave equations. Indiana Univ. Math. J. 44, 1273–1305 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  11. Hidano, K., Wang, C., Yokoyama, K.: The Glassey conjecture with radially symmetric data. J. Math. Pures Appl. (9) 98, 518–541 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  12. Hoshiro, T.: On weighted \(L^2\) estimates of solutions to wave equations. J. Anal. Math. 72, 127–140 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  13. John, F.: Blow-up of solutions of nonlinear wave equations in three space dimensions. Man. Math. 28, 235–268 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  14. John, F.: Blow-up for quasilinear wave equations in three space dimensions. Commun. Pure Appl. Math. 34, 29–51 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  15. Katayama, S.: Lifespan of solutions for two space dimensional wave equations with cubic nonlinearity. Commun. Partial Differ. Equ. 26, 205–232 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  16. Kato, T.: Blow-up of solutions of some nonlinear hyperbolic equations. Commun. Pure Appl. Math. 33, 501–505 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  17. Klainerman, S.: Remarks on the global Sobolev inequalities in the Minkowski space \({\mathbb{R}}^{n+1}\). Commun. Pure Appl. Math. 40, 111–117 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  18. Kubo, H., Kubota, K.: Asymptotic behaviors of radially symmetric solutions of \(\Box u=|u|^p\) for super critical values \(p\) in odd space dimensions. Hokkaido Math. J. 24, 287–336 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  19. Kubo, H., Kubota, K.: Asymptotic behaviors of radially symmetric solutions of \(\Box u=|u|^p\) for super critical values \(p\) in even space dimensions. Japan. J. Math. (N.S.) 24, 191–256 (1998)

    MathSciNet  MATH  Google Scholar 

  20. Lai, N.A., Zhou, Y.: An elementary proof of Strauss conjecture. J. Funct. Anal. 267, 1364–1381 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  21. Li, T.T., Zhou, Y.: A note on the life-span of classical solutions to nonlinear wave equations in four space dimensions. Indiana Univ. Math. J. 44, 1207–1248 (1995)

    MathSciNet  MATH  Google Scholar 

  22. Lindblad, H., Metcalfe, J., Sogge, C.D., Tohaneanu, M., Wang, C.: The Strauss conjecture on Kerr black hole backgrounds. Math. Ann. 359, 637–661 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  23. Lindblad, H., Sogge, C.D.: Long-time existence for small amplitude semilinear wave equations. Am. J. Math. 118, 1047–1135 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  24. Rammaha, M.A.: Finite-time blow-up for nonlinear wave equations in high dimensions. Commun. Partial Differ. Equ. 12, 677–700 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  25. Schaeffer, J.: The equation \(\Box u=|u|^p\) for the critical value \(p\). Proc. Roy. Soc. Edinburgh Sect. A 101, 31–44 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  26. Schaeffer, J.: Finite-time blow-up for \(u_{tt}-\Delta u=H(u_r,\, u_t)\). Commun. Partial Differ. Equ. 11, 513–543 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  27. Sideris, T.C.: Global behavior of solutions to nonlinear wave equations in three dimensions. Commun. Partial Differ. Equ. 8, 1291–1323 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  28. Sideris, T.C.: Nonexistence of global solutions to semilinear wave equations in high dimensions. J. Differ. Equ. 52, 378–406 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  29. Smith, H.F., Sogge, C.D., Wang, C.: Strichartz estimates for Dirichlet-wave equations in two dimensions with applications. Trans. Am. Math. Soc. 364, 3329–3347 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  30. Strauss, W.A.: Nonlinear scattering theory at low energy. J. Funct. Anal. 41, 110–133 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  31. Takamura, H.: Improved Kato’s lemma on ordinary differential inequality and its application to semilinear wave equations. Nonlinear Anal. 125, 227–240 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  32. Takamura, H., Wakasa, K.: The sharp upper bound of the lifespan of solutions to critical semilinear wave equations in high dimensions. J. Differ. Equ. 251, 1157–1171 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  33. Tataru, D.: Strichartz estimates in the hyperbolic space and global existence for the semilinear wave equation. Trans. Am. Math. Soc. 353, 795–807 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  34. Tzvetkov, N.: Existence of global solutions to nonlinear massless Dirac system and wave equation with small data. Tsukuba J. Math. 22, 193–211 (1998)

    MathSciNet  MATH  Google Scholar 

  35. Wang, C.: The Glassey conjecture on asymptotically flat manifolds. Trans. Am. Math. Soc. 367, 7429–7451 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  36. Wang, C.: The Glassey conjecture for nontrapping obstacles. J. Differ. Equ. 259, 510–530 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  37. Wang, C.: Long time existence for semilinear wave equations on asymptotically flat space-times. arXiv:1504.05652

  38. Yordanov, B.T., Zhang, Q.S.: Finite time blow up for critical wave equations in high dimensions. J. Funct. Anal. 231, 361–374 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  39. Zhou, Y.: Cauchy problem for semilinear wave equations in four space dimensions with small initial data. J. Partial Differ. Equ. 8, 135–144 (1995)

    MathSciNet  MATH  Google Scholar 

  40. Zhou, Y.: Blow up of solutions to the Cauchy problem for nonlinear wave equations. Chin. Ann. Math. Ser. B 22, 275–280 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  41. Zhou, Y.: Blow up of solutions to semilinear wave equations with critical exponent in high dimensions. Chin. Ann. Math. Ser. B 28, 205–212 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  42. Zhou, Y., Han, W.: Blow up of solutions to semilinear wave equations with variable coefficients and boundary. J. Math. Anal. Appl. 374, 585–601 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  43. Zhou, Y., Han, W.: Life-span of solutions to critical semilinear wave equations. Commun. Partial Differ. Equ. 39, 439–451 (2014)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Education, Mie University, 1577 Kurima-machiya-cho, Tsu, Mie, 514-8507, Japan

    Kunio Hidano

  2. School of Mathematical Sciences, Zhejiang University, Hangzhou, 310027, China

    Chengbo Wang

  3. Hokkaido University of Science, 7-15-4-1 Maeda, Teine-ku, Sapporo, Hokkaido, 006-8585, Japan

    Kazuyoshi Yokoyama

Authors
  1. Kunio Hidano
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chengbo Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kazuyoshi Yokoyama
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chengbo Wang.

Additional information

In memory of Rentaro Agemi.

The authors are very grateful to the referees for their helpful comments. K. Hidano was supported in part by the Grant-in-Aid for Scientific Research (C) (No. 23540198), Japan Society for the Promotion of Science (JSPS). C. Wang was supported by NSFC 11301478, 11271322, and Zhejiang Provincial Natural Science Foundation of China LR12A01002.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hidano, K., Wang, C. & Yokoyama, K. Combined effects of two nonlinearities in lifespan of small solutions to semi-linear wave equations. Math. Ann. 366, 667–694 (2016). https://doi.org/10.1007/s00208-015-1346-1

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00208-015-1346-1

Mathematics Subject Classification

Search

Navigation