1 Introduction

Ice mass changes (IMCs) of the Greenland ice sheet (GIS) and the Antarctic ice sheet (AIS) are important signs of global climate change. The main causes of IMC are changing surface mass balance (SMB) components (e.g. precipitation, surface melting, sublimation, wind drift) and changing ice flow dynamics (ID). In turn, IMCs induce global mass redistributions in the ocean and induce solid-Earth deformation: the elastic deformation due to present-day IMC and the viscoelastic deformation due to the isostatic adjustment to past IMC, i.e. the glacial isostatic adjustment (GIA). Satellite gravimetry and satellite altimetry measure these superimposed signals in terms of gravity change and elevation change, respectively, which allow to quantify GIA, IMC, and thereby the contribution of ice sheets to sea level change.

The GIA signals from geophysical forward models disagree significantly due to different assumptions on ice load histories, viscosity profiles (rheology), and the data and methods used to constrain such underlying assumptions (Whitehouse et al. 2019). In Greenland, GIA model outputs, expressed in terms of equivalent surface mass change, vary between −27 Gt \({\hbox {a}}^{-1}\) and \(+\)21 \(\text {Gt a}^{-1}\) according to Shepherd et al. (2019). The ice mass balance estimate of the GIS is −255 ± 20 \(\text {Gt a}^{-1}\) from 2005 to 2015 (Shepherd et al. 2019). GIA forward models in Antarctica vary between \(+\)3 \(\text {Gt a}^{-1}\) and \(+\)81 \(\text {Gt a}^{-1}\) according to Shepherd et al. (2018) and from \(+\)40 to \(+\)80 \(\text {Gt a}^{-1}\) according to Whitehouse et al. (2019). The ice mass balance of the AIS is −105 ± 51 \(\text {Gt a}^{-1}\) from 2003 until 2010 (Shepherd et al. 2018). In addition, a disagreement in the spatial patterns of GIA forward modelling results is evident to some extent for the GIS (Kappelsberger et al. 2021) and to a large extent for the AIS (Whitehouse et al. 2019). Furthermore, GIA from geophysical modelling would suggest a remarkable difference to GIA-induced bedrock motion observed with GNSS in Antarctica (MartínspsEspañol et al. 2016a) and in Greenland (Bevis et al. 2012; Kappelsberger et al. 2021). This difference raises questions on the rheological properties of the solid Earth. For example, Barletta et al. (2018) showed that the high rates of bedrock motion observed with GNSS in the Amundsen Embayment region can be explained by a GIA effect due to a low mantle viscosity. Such low viscosity implies that the present-day GIA is dominated by the recent decadal to centennial part of the ice loading history which is so far not included in global GIA modelling.

Wu et al. (2010), Rietbroek et al. (2016), and Jiang et al. (2021) demonstrated the inverse determination of GIA using geodetic data in a global framework as an alternative to relying on forward modelling results. Rietbroek et al. (2016) co-estimated GIA in a global inversion framework using GRACE and ocean altimetry data. They used five globally consistent GIA fingerprints from geophysical GIA modelling by Klemann and Martinec (2011) which are based on regional ice histories. Rietbroek et al. (2016) found that the Antarctic a priori fingerprint needed to be downscaled to 18% of the initial fingerprint magnitude to obtain the best fit to the data. The GIA fingerprint of Greenland is scaled to 77% of its original magnitude. As a reason for the downscaling of the prescribed Antarctic GIA pattern, we suspect that the true GIA pattern and the prescribed GIA pattern are incompatible. Thus, the true GIA cannot be effectively resolved by any scaling of the prescribed GIA pattern (cf. Fig. S3). In consequence, the unresolved GIA signals are misattributed as IMC signals and vice versa. Jiang et al. (2021) incorporated the GIA signal-covariance information in a global inversion framework to loosen the dependence on geophysical modelling results and to enable the revealing of GIA effects that are not predicted by geophysical GIA modelling.

In order to derive IMC and GIA over ice sheets without relying on GIA forward models, regional inversions have combined geodetic satellite observations in Antarctica (Riva et al. 2009; Gunter et al. 2014; Martín-Español et al. 2016b; Sasgen et al. 2017; Engels et al. 2018). Gunter et al. (2014) combined satellite gravimetry, altimetry, and climate modelling products and provided regionally robust estimates of IMC and GIA. Engels et al. (2018) built on this approach and, with the additional inclusion of GNSS, determined present-day GIA and IMC with an increased spatial resolution. In contrast, Martín-Español et al. (2016b) applied a statistical modelling approach. In this approach, the authors derived the spatio-temporal characteristics of the signals over the AIS from forward models and quantified the signals in a Bayesian framework using observations from satellite gravimetry, altimetry, and GNSS. These three types of observation are also used in the data combination approach by Sasgen et al. (2017), while this framework allows for determining lateral rheological heterogeneities. These regional inversions presented strategies for obtaining spatially resolved estimates of the present-day GIA effect in Antarctica. However, these approaches cannot simply be utilized in a global inversion framework. One reason is that these approaches implement regional constraints to remove bias in the GIA estimate (Willen et al. 2020).

Here, we present a global inversion framework with the aim to improve the co-estimation of GIA and IMC from satellite observations over ice sheets. This approach incorporates three empirical estimation strategies: First, the approach uses the combination of satellite gravimetry and altimetry with climate and firn modelling products (Gunter et al. 2014). Second, it builds on the estimation, in a global framework, of scaling factors for GIA fingerprints related to the deglaciation of particular regions (‘regional GIA fingerprints’) (Rietbroek et al. 2016). Finally, the inversion framework makes use of GIA patterns related to localized deglaciation impulses (‘local GIA fingerprints’) for parametrizing GIA without relying an a priori regional pattern (Sasgen et al. 2017). The GIA parametrization by local GIA fingerprints is applied for GIA associated to Antarctica where GIA patterns from forward models are particularly unreliable, as discussed above. The presented approach combines observations of satellite gravimetry, satellite altimetry over the AIS and the GIS, as well as climate and firn model products over both ice sheets. Furthermore, the approach incorporates a parametrization of volume changes of the ice sheets’ firn layer inherent in satellite altimetry observations, in order to accommodate errors of climate and firn modelling results in quantifying these firn volume changes.

We analyse the feasibility of this approach using simulated signals and observations. We investigate the quality of the estimates for ice mass change, firn volume change, and GIA that can be expected depending on the input data quality. For this purpose, we simulate realistic errors of the observations based on error covariances assessed from real data. We perform three simulation experiments: (1) The observations solely contain the geophysical signals without any error. (2) The observations contain the geophysical signals and correlated errors, but we only assume uncorrelated errors in the parameter estimation. (3) The observations contain the geophysical signals and correlated errors. We account for the error covariances in the parameter estimation. We perform these three experiments with two variants of simulated observations. These two variants differ in terms of the GIA model output that is used to generate the observations. To simplify the simulation experiments, we focus on mass effects due to IMC of ice sheets and GIA only and do not investigate the ocean mass change contributors hydrology and glaciers in this study. But eventually in a full inversion evaluating real data, we will make use of a parametrization accounting all contributors (e.g. Rietbroek et al. 2016).

Section 2 introduces the physical quantities and their relation to the observations over the ice sheets. In Sect. 3, we present the methodology of the inversion approach and describe how we set up the simulation environment. We show the results of the simulation experiments in Sect. 4 and discuss them in Sect. 5. The Supplementary Material (SM) provides supporting information.

2 Theoretical background

We express temporal gravity field changes as equivalent surface density changes in a spherical layer (also referred to as area density changes) with the unit of mass per surface area. The surface density change \(\Delta \kappa \) at a position \(\varvec{x}\) can be developed into a series of spherical harmonic basis functions \(Y_{nm}\) of degree n and order m:

$$\begin{aligned} \Delta \kappa (\varvec{x}) = \sum _{n=0}^{\infty } \sum _{m=-n}^{n} \Delta \kappa _{nm} Y_{nm} (\varvec{x}). \end{aligned}$$
(1)

Following Wahr et al. (1998), a change of a Stokes coefficient (\(\Delta c_{nm}\)) is converted to the spherical harmonic coefficient of a surface density change

$$\begin{aligned} \Delta \kappa _{nm} = \frac{2n + 1}{1 + k'_n} \frac{M_E}{4 \pi R^2} \Delta c_{nm}, \end{aligned}$$
(2)

where \(M_E\) is the total mass of the Earth, R the semi-major axis of the reference ellipsoid, and \(k'_n\) the load Love number to account for the elastic solid-Earth deformation induced by surface load variations.

We express the temporal change of physical quantities (gravity, mass, volume, etc.) over a certain time period by a mean rate of change over this period. This mean rate is obtained in practice from fitting a linear function to the underlying time series. Although arising from a linear regression, the mean rates do not intend to isolate any intrinsically linear process. Therefore, nonlinear signals contained in the time series are not a source of error for the determination of the mean rates.

Mass redistributions due to GIA in the solid Earth (and to a lesser extent in the ocean) lead to a change of Earth’s gravity field, which can be expressed as the equivalent surface density rate \({\dot{\kappa }}^{{\textsc {gia}}}\). Likewise, mass changes of ice sheets and the induced ocean mass change and the elastic load deformation of the solid Earth lead to gravity field changes which can be expressed by their equivalent surface mass change \({\dot{\kappa }}^{{\textsc {imc}}}\). The surface density rate \({\dot{\kappa }}^{{\textsc {total}}}\)

$$\begin{aligned} {\dot{\kappa }}^{{\textsc {total}}} = {\dot{\kappa }}^{{\textsc {imc}}} + {\dot{\kappa }}^{{\textsc {gia}}} + {\dot{\kappa }}^{{\textsc {other}}}, \end{aligned}$$
(3)

contains the IMC and GIA effects together with other effects (\({\dot{\kappa }}^{{\textsc {other}}}\)) such as terrestrial water mass changes that we do not consider here, explicitly. Contributions from changing SMB, \({\dot{\kappa }}^{{\textsc {smb}}}\), and changing ice dynamics, \({\dot{\kappa }}^{{\textsc {id}}}\), induce IMC which can be expressed as the sum of surface density rates in the firn layer (\({\dot{\kappa }}^{{\textsc {firn}}}\)) and surface density rates in the ice layer (\({\dot{\kappa }}^{{\textsc {ice}}}\)) of an ice sheet

$$\begin{aligned} {\dot{\kappa }}^{{\textsc {imc}}} = {\dot{\kappa }}^{{\textsc {firn}}} + {\dot{\kappa }}^{{\textsc {ice}}}. \end{aligned}$$
(4)

For a large part \({\dot{\kappa }}^{{\textsc {firn}}}\) is induced by changing SMB, and \({\dot{\kappa }}^{{\textsc {ice}}}\) by changing ice dynamics.

The surface elevation rate over ice sheets, \({\dot{h}}^{{\textsc {total}}}\), is the sum of elevation changes in the ice layer (\({\dot{h}}^{{\textsc {ice}}}\)), firn thickness change (\({\dot{h}}^{{\textsc {firn}}}\)), the deformation of the solid Earth surface (bedrock motion) due to GIA (\({\dot{h}}^{{\textsc {gia}}}\)) as well as the elastic-induced bedrock motion due to present-day load variations (\({\dot{h}}^{{\textsc {ela}}}\)):

$$\begin{aligned} {\dot{h}}^{{\textsc {total}}} = {\dot{h}}^{{\textsc {ice}}} + {\dot{h}}^{{\textsc {firn}}} + {\dot{h}}^{{\textsc {gia}}} + {\dot{h}}^{{\textsc {ela}}}. \end{aligned}$$
(5)

Analogous to \({\dot{\kappa }}^{{\textsc {ice}}}\), \({\dot{h}}^{{\textsc {ice}}}\) is for a large part due to changing ice dynamics. The density of pure ice (\(\rho ^{{\textsc {ice}}} = \)917 kg m−3) links changes of the surface elevation in the ice layer \({\dot{h}}^{{\textsc {ice}}}\) and of the surface density \({\dot{\kappa }}^{{\textsc {ice}}}\):

$$\begin{aligned} {\dot{h}}^{{\textsc {ice}}} = \frac{{\dot{\kappa }}^{{\textsc {ice}}}}{\rho ^{{\textsc {ice}}}}. \end{aligned}$$
(6)

The firn thickness change \({\dot{h}}^{{\textsc {firn}}}\) and the surface density rate in the firn layer \({\dot{\kappa }}^{{\textsc {firn}}}\) can be related by a firn density \(\rho ^{{\textsc {firn}}}\):

$$\begin{aligned} {\dot{h}}^{{\textsc {firn}}} = \frac{{\dot{\kappa }}^{{\textsc {firn}}}}{\rho ^{{\textsc {firn}}}}. \end{aligned}$$
(7)

Alternatively, volume changes of the ice sheet’s firn layer can be described using changes of the firn air content (FAC) \({\dot{h}}^{{\textsc {fac}}}\) (Ligtenberg et al. 2014). This enables the avoidance of the firn density. Instead of Eq. 7 we can write

$$\begin{aligned} {\dot{h}}^{{\textsc {firn}}} = \frac{{\dot{\kappa }}^{{\textsc {firn}}}}{\rho ^{{\textsc {ice}}}} + {\dot{h}}^{{\textsc {fac}}}. \end{aligned}$$
(8)

We can rewrite Eq. 5 as

$$\begin{aligned} {\dot{h}}^{{\textsc {total}}} = {\dot{h}}^{{\textsc {imc}}} + {\dot{h}}^{{\textsc {fac}}} + {\dot{h}}^{{\textsc {gia}}} + {\dot{h}}^{{\textsc {ela}}}, \end{aligned}$$
(9)

where

$$\begin{aligned} {\dot{h}}^{{\textsc {imc}}} = \frac{{\dot{\kappa }}^{{\textsc {imc}}}}{\rho ^{{\textsc {ice}}}} = \frac{{\dot{\kappa }}^{{\textsc {firn}}} + {\dot{\kappa }}^{{\textsc {ice}}}}{\rho ^{{\textsc {ice}}}} = \frac{{\dot{\kappa }}^{{\textsc {firn}}}}{\rho ^{{\textsc {ice}}}} + {\dot{h}}^{{\textsc {ice}}}. \end{aligned}$$
(10)

3 Materials and methods

3.1 Inversion approach

Our aim is to jointly estimate GIA and IMC for both ice sheets (GIS and AIS) from satellite gravimetry and satellite altimetry. Unlike other combination strategies (e.g. Gunter et al. 2014), we do not suggest to address the effect of firn processes in the altimetry observations by correcting for modelled firn thickness changes in a deterministic manner. Instead, we use modelled FAC as an additional observation subject to uncertainties, and we co-estimate FAC jointly with GIA and IMC.

We set up a Gauss–Markov-model (or general linear model or general regression model) (e.g. Koch 1999),

$$\begin{aligned} \varvec{d} + \varvec{e} = \varvec{X}\varvec{\beta } \quad \text {with} \quad C(\varvec{d}) = \sigma ^2 \varvec{P}^{-1}, \end{aligned}$$
(11)

where the observations assembled in the vector \(\varvec{d}\) are linked to the sought-for parameters assembled in the vector \(\varvec{\beta }\) by the design matrix \(\varvec{X}\). The vector \(\varvec{e}\) contains the residuals, \(C(\varvec{d})\) is the covariance matrix of the observation errors, \(\varvec{P}\) is the weight matrix and \(\sigma ^2\) is the factor of unit weight. The estimate \(\varvec{{\hat{\beta }}}\) of the parameters \(\varvec{\beta }\) and the error covariance of the estimate \(C(\varvec{{\hat{\beta }}})\) are calculated by generalized least squares adjustment (e.g. Koch 1999) as

$$\begin{aligned} \varvec{{\hat{\beta }}} = {(\varvec{X}^{\textsc {T}} \varvec{P} \varvec{X})}^{-1} \varvec{X}^{\textsc {T}} \varvec{P} \varvec{d} \qquad \text {and} \qquad C(\varvec{{\hat{\beta }}}) = \sigma ^2 {(\varvec{X}^{\textsc {T}} \varvec{P} \varvec{X})}^{-1}. \end{aligned}$$
(12)

More specifically, the observation vector \(\varvec{d}\) assembles the following observations subject to errors \(\varvec{\varepsilon }\): satellite gravimetry data,

$$\begin{aligned} \varvec{d}^{\textsc {grav}} = F^{{\textsc {grav}}}({\dot{\kappa }}^{{\textsc {total}}}) + \varvec{\varepsilon }^{{\textsc {grav}}}, \end{aligned}$$
(13)

represented as a set of spherical harmonic coefficients of surface mass density change and containing the superimposed signals according to (3). \(F^{{\textsc {grav}}}\) is the forward operator, that maps the signal \({\dot{\kappa }}^{{\textsc {total}}}\) into the discrete gravimetry observations. The ice-sheet surface elevation changes observed by altimetry with the altimetry forward operator \(F^{{\textsc {alt}}}\),

$$\begin{aligned} \varvec{d}^{\textsc {alt}} = F^{{\textsc {alt}}}({\dot{h}}^{{\textsc {total}}}) + \varvec{\varepsilon }^{{\textsc {alt}}}, \end{aligned}$$
(14)

are expressed in spatial grids covering the ice sheets and contain the superimposed signals according to (5) and (9). The modelled FAC changes with the forward operator \(F^{{\textsc {fac}}}\),

$$\begin{aligned} \varvec{d}^{\textsc {fac}} = F^{{\textsc {fac}}}({\dot{h}}^{{\textsc {fac}}}) + \varvec{\varepsilon }^{{\textsc {fac}}}, \end{aligned}$$
(15)

are likewise expressed in grids over the ice sheets and contain the signal expressed by (8).

The parameter vector \(\varvec{\beta }\) contains parameters related to GIA (\(\varvec{\beta }^{{\textsc {gia}}}\)), to IMC (\(\varvec{\beta }^{{\textsc {IMC}}}\)) and to FAC (\(\varvec{\beta }^{{\textsc {FAC}}}\)). An additional distinction of parts related exclusively to the AIS or the GIS is indicated by according superscripts and subscripts. Hence, the observation equation (11) reads

$$\begin{aligned}&\begin{pmatrix} \varvec{d}^{\textsc {grav}} \\ \varvec{d}^{\textsc {gis-\!\!alt}} \\ \varvec{d}^{\textsc {gis-\!\!fac}} \\ \varvec{d}^{\textsc {ais-\!\!alt}} \\ \varvec{d}^{\textsc {ais-\!\!fac}} \end{pmatrix} + \varvec{e}\nonumber \\&\quad = \begin{pmatrix} \varvec{X}_{\textsc {gia}}^{\textsc {grav}} &{} \varvec{X}_{\textsc {gis-\!\!imc}}^{\textsc {grav}} &{} \varvec{0} &{} \varvec{X}_{\textsc {ais-\!\!imc}}^{\textsc {grav}} &{} \varvec{0} \\ \varvec{X}_{\textsc {gia}}^{\textsc {gis-\!\!alt}} &{} \varvec{X}_{\textsc {gis-\!\!imc}}^{\textsc {gis-\!\!alt}} &{} \varvec{X}_{\textsc {gis-\!\!fac}}^{\textsc {gis-\!\!alt}} &{} \varvec{X}_{\textsc {ais-\!\!imc}}^{\textsc {gis-\!\!alt}} &{} \varvec{0} \\ \varvec{0} &{} \varvec{0} &{} \varvec{X}_{\textsc {gis-\!\!fac}}^{\textsc {gis-\!\!fac}} &{} \varvec{0} &{} \varvec{0} \\ \varvec{X}_{\textsc {gia}}^{\textsc {ais-\!\!alt}} &{} \varvec{X}_{\textsc {gis-\!\!imc}}^{\textsc {ais-\!\!alt}} &{} \varvec{0} &{} \varvec{X}_{\textsc {ais-\!\!imc}}^{\textsc {ais-\!\!alt}} &{} \varvec{X}_{\textsc {ais-\!\!fac}}^{\textsc {ais-\!\!alt}} \\ \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{0} &{} \varvec{X}_{\textsc {ais-\!\!fac}}^{\textsc {ais-\!\!fac}} \\ \end{pmatrix}\nonumber \\&\qquad \cdot \begin{pmatrix} \varvec{\beta }_{\textsc {gia}} \\ \varvec{\beta }_{\textsc {gis-\!\!imc}} \\ \varvec{\beta }_{\textsc {gis-\!\!fac}} \\ \varvec{\beta }_{\textsc {ais-\!\!imc}} \\ \varvec{\beta }_{\textsc {ais-\!\!fac}} \end{pmatrix}. \end{aligned}$$
(16)

We describe the parametrization and the setup of the design matrix in Sect. 3.2. The description of the simulated observations and their error covariance information follows in Sects. 3.3 and 3.4, respectively.

Fig. 1
figure 1

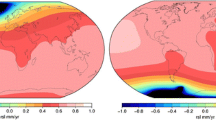
a The global pattern of the present-day GIA effect of a generic ice history at one position in Antarctica, i.e. the normalized deglaciation impulse response. The blue line indicates the section shown in (b). Globally consistent GIA patterns were calculated for all highlighted positions (black dots). b The section of the GIA pattern along a part of the meridian of the deglaciation impulse centre shown in (a). The lower x-axis is the ellipsoidal distance along the meridian from the centre of the deglaciation impulse. The upper x-axis is the latitude along the meridian. The green point in (a, b) highlights the South Pole

Full size image

3.2 Parametrization of signals

Glacial isostatic adjustment (GIA)Rietbroek et al. (2016) and Sun and Riva (2020) demonstrated that fitting globally consistent fingerprints from GIA forward modelling to GRACE observations in a global inversion framework represents a promising strategy to estimate the GIA signal. However, as mentioned in Sect. 1, the GIA signal predicted by geophysical models over Antarctica is uncertain (Shepherd et al. 2018; Whitehouse et al. 2019). Whitehouse et al. (2019) showed that not just the magnitude but also the spatial pattern of several GIA modelling results varies significantly (Fig. 2 therein). The GIA patterns predicted by different models are so different that scaling of one pattern cannot reproduce another pattern. Moreover, we showed in a test experiment that scaling a pattern inferred from a single GIA model is inappropriate to resolve the pattern predicted by an another GIA model (cf. Fig. S3). Albeit Rietbroek et al. (2016) implemented a single Antarctic GIA pattern that disagrees with GNSS observations for large parts (Thomas et al. 2011). We suspect that using a single Antarctic GIA fingerprint with inherent modelling errors—as done by Rietbroek et al. (2016)—might be insufficient to resolve discrepancies between observations and model predictions. This presumably leads to the significant damping of the Antarctic GIA fingerprint in the inversion results. Here, we propose an extension of the fingerprint parametrization for Antarctica. In case of Greenland, we argue that the parametrization using a single fingerprint is appropriate, because the GIA pattern does not need to be scaled as extensively to fit the data in Rietbroek et al. (2016). Thus, we apply two methodological approaches of either a more model-independent (AIS) or a more model-dependent (GIS) GIA parametrization.

We parametrize GIA due to Antarctic glacial history based on B globally consistent GIA patterns. Each pattern is based on a generic glacial history at a single position represented by a disk-shaped element on the Tegmark-grid (Tegmark 1996) used by the SELEN software (Spada and Melini 2019). The glacial history is a step function in time where at 10 ka before present an ice column is removed. This timing is motivated by the approximate beginning of the Holocene. For the generic glacial ‘impulses’ defined this way we model the globally consistent viscoelastic response with the SELEN software. These resulting GIA responses may be interpreted as ‘GIA mascons’ or ‘globally consistent GIA radial-like basis functions’. The shape of the GIA response to a deglaciation impulse is similar to a Gaussian function (“bell curve”) with a half response radius and one-sigma radius of \(\sim \)300 and \(\sim \)250 km, respectively (Fig. 1). The choice of the generic deglaciation history and the rheology could be chosen within wide limits, they induce patterns of present-day GIA gravity field rates and bedrock motion rates that are similar to patterns induced by different rheology and different deglaciation histories, limited to the same local deglaciation source. Therefore, the parametrized patterns may capture a large range of realistic GIA signals.

We considered those AIS nodes of the Tegmark grid that have an ice layer in the ICE-6G glacial history leading to a full coverage of the Antarctic continent. We assume that the ICE-6G glaciation history does not miss any larger regions of deglaciation since the last glacial maximum. To reduce the parameter space, we decimate the grid to an approximate spacing of 250 km, justified by the shape of the response functions. Thus we obtain \(B=189\) Antarctic GIA parameters related to 189 positions shown in Fig. 1a. Section 5 provides further discussion of the chosen properties of these GIA patterns.

Outside Antarctica, we parametrize GIA due to the glacial history in Greenland, Laurentia, Fennoskandia, and other regions (Patagonia, Barents and Kara Sea, etc., referred to as Other) by 4 fingerprints from forward modelling similar to fingerprints from Klemann and Martinec (2011) used in Rietbroek et al. (2016). We generate these fingerprints by GIA forward modelling using the SELEN software package (Spada and Melini 2019). We isolated the ICE-6G glacial history (Stuhne and Peltier 2015) for each region and model the GIA signal which would result solely from the loading variation in the selected regions. All model runs use the Green’s function based on VM5a rheology included in the SELEN software package. Caron et al. (2018) found that the C\(_{\text {21}}\)-S\(_{\text {21}}\)-pattern of their optimized GIA result differed systematically from the modelling result by Purcell et al. (2016) which is based on the ICE-6G ice history with VM5a rheology (Figure S2 in Caron et al. 2018). Caron et al. (2018) attribute this difference in the rotational feedback to an underestimated mantle viscosity in their GIA result. We additionally include 2 fingerprints (one for C\(_{\text {21}}\) and one for S\(_{\text {21}}\)) to capture a potential residual GIA-induced rotational feedback component that the other fingerprints do not account for.

The GIA parameters \(\varvec{\beta }_{\textsc {gia}}\) are scaling factors for each of the \(B+6\) prescribed global GIA patterns: B local Antarctic patterns, 4 regional patterns, and 2 polar motion patterns. With \(\varvec{\xi }_1 \ldots \varvec{\xi }_{B+6}\) denoting the representation of these patterns in terms of the SH coefficients of the equivalent surface density trends, the block of the design matrix \(\varvec{X}_{\textsc {gia}}^{\textsc {grav}}\) that links satellite gravimetry observations to GIA is

$$\begin{aligned} \varvec{X}_{\textsc {gia}}^{\textsc {grav}} = \begin{pmatrix} \varvec{\xi }_1&\varvec{\xi }_2&\dots&\varvec{\xi }_{B+6} \end{pmatrix}. \end{aligned}$$
(17)

The blocks of the design matrix \(\varvec{X}_{\textsc {gia}}^{\textsc {ais-\!\!alt}}\) and \(\varvec{X}_{\textsc {gia}}^{\textsc {gis-\!\!alt}}\) that link observed surface elevation changes to the parametrized GIA patterns realize the evaluation of GIA-induced bedrock motion in the spatial domain at the positions of the AIS and GIS grid nodes. For this purpose, the modelling results from SELEN, representing the present-day geometric changes, are used.

Hence, each row of \(\varvec{X}_{\textsc {gia}}^{\textsc {ais-\!\!alt}}\) (and \(\varvec{X}_{\textsc {gia}}^{\textsc {gis-\!\!alt}}\), respectively) contains the \(B+6\) parametrized bedrock-motion GIA patterns evaluated at the grid position to which the row refers.

Once the GIA parameters are estimated as \({\hat{\beta }}_{1}^{{\textsc {gia}}} \dots {\hat{\beta }}_{B+6}^{{\textsc {gia}}}\), the estimated GIA signal at a position \(\varvec{x}\) is the weighted superposition of the GIA patterns:

$$\begin{aligned} \hat{{\dot{\kappa }}}^{{\textsc {gia}}} (\varvec{x}) = \sum _{b=1}^{B+6} {\hat{\beta }}_{b}^{{\textsc {gia}}} \, \xi _{b} (\varvec{x}). \end{aligned}$$
(18)

We use the software SELEN4 (Spada and Melini 2019) for the computation, because it is a publicly available open-source program and allows the gravitationally and topographically self-consistent solving of the sea level equation. Furthermore, the rotational feedback and the migration of shorelines are taken into account. So far, a 1-D Maxwell rheological profile is used.

We perform test experiments to demonstrate to what extent the GIA parametrization is suitable to reproduce GIA signals induced by different glacial histories and different Earth rheologies (Figs. S2–S5). The first test experiment uses a global GIA signal that we model in the similar environment as we use it for generating the GIA parameters, i.e. the SELEN software run by ICE-6G ice history and VM5a rheology. In the second and third experiment, we fit the parameters to the present-day GIA signal from Caron et al. (2018). We can resolve the GIA signal when we include the C\(_{\text {21}}\) and S\(_{\text {21}}\) fingerprints demonstrated by the second test experiment (Fig. S3). However, in the third test experiment we exclude the C\(_{\text {21}}\) and S\(_{\text {21}}\) fingerprints to demonstrate their necessity. Doing so, we could only partly resolve the original GIA signal due to discrepancies of the C\(_{\text {21}}\) and S\(_{\text {21}}\) coefficients between the GIA model from Caron et al. (2018) and the parametrization (Fig. S4c, Figure S2 in Caron et al. 2018). The fourth test experiment is a regional fit in the spatial domain of the present-day GIA signal found by Barletta et al. (2018).

Ice mass change (IMC) We parametrize IMC based on two grids in Greenland and Antarctica. The grids are located over the grounded ice sheets with a resolution of 50 km \(\times \) 50 km using the polar stereographic projections EPSG:3413 and EPSG:3031 for GIS and AIS, respectively. This resolution allows a spatially resolved estimation of IMC, similar to other GRACE-derived products (Groh and Horwath 2021) and is not computationally expensive. We assign a mass change to each grid cell i with an area A. This mass change is transferred to the spherical-harmonic domain by assuming this mass change is concentrated in a point (Pollack 1973). This is done up to the maximum degree of 96 according to how GRACE monthly gravity fields are provided (e.g. Mayer-Gürr et al. 2018). We solve the sea level equation (Farrell and Clark 1976) for each mass change to ensure mass conservation in the Earth system. Thereby, we assume the ice sheets only exchange mass with the ocean. The globally consistent set of spherical harmonic coefficients related to the i-th point mass is \(\varvec{\psi }_{i}\). Furthermore, each \(\varvec{\psi }_{i}\) can be transferred in the spatial domain.

The matrix blocks of the design matrix which link the gravimetry observations to the IMC-induced surface density rate are \(\varvec{X}_{\textsc {gis-\!\!imc}}^{\textsc {grav}}\) and \(\varvec{X}_{\textsc {ais-\!\!imc}}^{\textsc {grav}}\), each with a number of columns equal to the number of grid cells either in Greenland u or Antarctica v:

$$\begin{aligned} \varvec{X}_{\textsc {gis-\!\!imc}}^{\textsc {grav}}= & {} \begin{pmatrix} \varvec{\psi }_1&\varvec{\psi }_2&\dots&\varvec{\psi }_u \end{pmatrix}\nonumber \\ \varvec{X}_{\textsc {ais-\!\!imc}}^{\textsc {grav}}= & {} \begin{pmatrix} \varvec{\psi }_1&\varvec{\psi }_2&\dots&\varvec{\psi }_v \end{pmatrix}. \end{aligned}$$
(19)

\(\varvec{X}_{\textsc {gis-\!\!imc}}^{\textsc {gis-\!\!alt}}\) and \(\varvec{X}_{\textsc {ais-\!\!imc}}^{\textsc {ais-\!\!alt}}\) link the satellite altimetry observations of the indicated ice sheet to the surface elevation change caused by IMC and to the IMC-induced elastic deformation. Note that we retrieve the elastic pattern of the mass change in each pixel by solving the sea level equation up to degree 400 to obtain the intended altimetry resolution of 50 km (Sect. 3.3). \(\varvec{X}_{\textsc {ais-\!\!imc}}^{\textsc {gis-\!\!alt}}\) and \(\varvec{X}_{\textsc {gis-\!\!imc}}^{\textsc {ais-\!\!alt}}\) formally account for the global elastic effect of AIS IMC on the altimetry observations over GIS and vice versa. Note that these effects are negligibly small.

The parameter being estimated is the scaling factor of the mass rate in each grid cell i (\(\hat{\beta _{i}}^{{\textsc {imc}}}\)). Assuming a mass rate of 1 kg a−1, we can write

$$\begin{aligned} \hat{\beta _{i}}^{{\textsc {imc}}} \cdot 1\,\text {kg\,a}^{-\text {1}} = \hat{{\dot{\kappa }}}_{i}^{{\textsc {imc}}} A_{i}. \end{aligned}$$
(20)

Firn Air Content (FAC) Similar to IMC, we use two grids over the grounded ice sheets in Greenland and Antarctica to parametrize FAC. The blocks of the design matrix which link the altimetry observations to changes of FAC (\(\varvec{X}_{\textsc {gis-\!\!fac}}^{\textsc {gis-\!\!alt}}\) and \(\varvec{X}_{\textsc {gis-\!\!fac}}^{\textsc {gis-\!\!alt}}\)) are identity matrices here, because we use the same grids for the observations and parametrization (cf. Sect. 3.3). Likewise \(\varvec{X}_{\textsc {gis-\!\!fac}}^{\textsc {gis-\!\!fac}}\) and \(\varvec{X}_{\textsc {ais-\!\!fac}}^{\textsc {ais-\!\!fac}}\) are identity matrices.

The parameter being estimated is the scaling factor of the FAC-related elevation rate in the grid cell i (\({\hat{\beta }}_{i}^{{\textsc {fac}}}\)). Assuming an elevation rate of 1 m a−1, we can write

$$\begin{aligned} {\hat{\beta }}_{i}^{{\textsc {fac}}} \cdot 1\,\text {m\,a}^{-\text {1}} = \hat{{\dot{h}}}_{i}^{{\textsc {fac}}}. \end{aligned}$$
(21)

3.3 Synthetic signals and observables

In this section, we describe the synthetic environment we use for the simulation experiments. To this end, we generate synthetic signals, i.e. mean rates over a 10-year period for GIA, IMC (ID and SMB), and FAC, which represent the synthetic true signals in our investigations (Fig. 2). We choose a 10-year period according to the availability of real data sets (cf. Sect. 5.1). From those signals we compute observations (Fig. 3). We simulate satellite gravimetry observations and satellite altimetry observations. Additionally we use products from regional climate and firn modelling to simulate pseudo-observations for FAC. We use the same grids for altimetry and FAC observations and for the IMC and FAC parametrization (Sect. 3.2).

Fig. 2
figure 2

The synthetic signals for GIS (a–f) and AIS (g–l) used for variant A of synthetic observations: bedrock motion due to glacial isostatic adjustment (GIA), surface density change due to ice dynamics (ID), surface density change due to surface mass balance (SMB), elevation change due to firn thickness change from firn densification modelling (FDM), the rate of the firn air content (FAC), and the elastic signal due to surface load changes. Figure S1 illustrates the GIA signal from Caron et al. (2018) which we use for generating variant B of synthetic observations

Full size image
Fig. 3
figure 3

The synthetic gravimetry (first column), altimetry observations (second column), and FAC data (third column) for GIS (a–f) and AIS (g–l) without errors (a–c and g–i) and including errors (d–f and j–l). We transferred the gravimetry observations to the spatial domain for illustration. We provide a figure of the errors in the SM (Fig. S3)

Full size image

We generate the synthetic GIA signal (Fig. 2a+g) for the first variant of observations (variant A) by forward modelling using SELEN with the ICE-6G glacial history (Spada and Melini 2019). The Stokes coefficients are converted to coefficients of surface densities using Eq. 2. The model output of the bedrock motion expressed by its spherical harmonic coefficients is transferred into the spatial domain. For the second variant of observations (variant B), we use the GIA modelling output from Caron et al. (2018) which represents an alternative GIA model derived from a different modelling environment.

The RACMO2 SMB modelling product (Noël et al. 2018; van Wessem et al. 2018) is the basis to compute \({\dot{\kappa }}^{{\textsc {smb}}}\). We estimate changes of the SMB with respect to a reference period. We choose the whole modelling period from Jan 1979 to Dec 2016 as the reference period. This is consistent with the reference period of the IMAU-FDM firn thickness change product (Ligtenberg et al. 2011). We remove the mean SMB over this reference period from the SMB values to calculate the surface mass balance anomalies and we cumulate the anomalies, which is referred to as cumulated SMB anomalies. We define \({\dot{\kappa }}^{{\textsc {smb}}}\) (Fig. 2c+i) as the least-squares estimated rate of cumulated SMB anomalies from Jan 2003 until Dec 2012. The rate of the SMB-driven contribution to the mass balances obtained in this way is −163 \(\text {Gt a}^{-1}\) (GIS) and −6 \(\text {Gt a}^{-1}\) (AIS).

Similarly, we obtain \({\dot{h}}^{{\textsc {firn}}}\) from the IMAU-FDM firn thickness change product (Ligtenberg et al. 2011). \({\dot{h}}^{{\textsc {firn}}}\) (Fig. 2d+j) is the least-squares estimated rate of the firn-thickness change time series from Jan 2003 until Dec 2012. We obtain FAC (Fig. 2e+k) from \({\dot{\kappa }}^{{\textsc {smb}}}\) and \({\dot{h}}^{{\textsc {firn}}}\) following Eq. 8. In result, the simulated volume rate of the FAC is −289 km3a−1 and −10 km3a−1 for the GIS and the AIS, respectively.

The synthetic ID signal (Fig. 2b+h) is obtained from altimetry observations over ice sheets. We use the linear surface elevation rates from altimetry observations (Schröder et al. 2019; Strößenreuther et al. 2020) to define these signals with a minimum threshold of 0.05 m a−1 of the absolute value of the observed surface elevation rate. Additionally in Antarctica, we apply a mask based on McMillan et al. (2014) to define regions where we assume ID-driven mass changes. In Greenland, we apply a mask based on ice flow velocities from Joughin et al. (2018) and use a minimum threshold of 1 m a−1 to define regions where we assume ID-driven mass changes. We use \(\rho ^{{\textsc {ice}}}\) of 917 kg m−3 to convert surface elevation rates into surface density rates. The simulated rates of the ID-driven contribution to the mass balances are −79 \(\text {Gt a}^{-1}\) (GIS) and −109 \(\text {Gt a}^{-1}\) (AIS). The obtained total rate of IMC is −243 \(\text {Gt a}^{-1}\) (GIS) and −115 \(\text {Gt a}^{-1}\) (AIS).

To simulate gravimetry observations (Fig. 3a+g), we generate spherical harmonic coefficients of the surface density rate in kg m−2 a−1 up to degree and order 96 according to a typical GRACE level 2 product (e.g. Mayer-Gürr et al. 2018) which allows a theoretical resolution up to approximately 208 km. To do so, we generate globally consistent coefficients of IMC from the synthetic IMC defined on the grids which include the ocean response and solid-Earth elastic response. First, we convert the mass change of each grid cell into its spherical harmonic point mass representation (Pollack 1973) and calculate the sum over all grid cells. Second, we solve the sea level equation (Farrell and Clark 1976) to achieve mass conservation in the Earth system. Along with this step we compute the elastic deformation of the solid Earth due to IMC (Fig. 2f+l). The synthetic gravimetry observable is the sum of the globally consistent IMC coefficients and the GIA surface density rates (Eq. 3).

The synthetic altimetry observable (Fig. 3b+h) is the sum of the synthetic gridded surface elevation rates due to ID, firn thickness change, GIA, and elastic bedrock motion (Eq. 5), evaluated over the grid for GIS and AIS.

3.4 Stochastic error characterization

We represent the covariance matrix \(C(\varvec{d})\) as a composite block matrix of the \([l \times l]\) covariance matrices \(C(\varvec{d}^{\textsc {grav}})\), \(C(\varvec{d}^{\textsc {gis-\!\!alt}})\), \(C(\varvec{d}^{\textsc {gis-\!\!fac}})\), \(C(\varvec{d}^{\textsc {ais-alt}})\), and \(C(\varvec{d}^{\textsc {ais-fac}})\). In case of gravimetry observations, \(l=(n+1)^2-1\), the number of spherical harmonic coefficients. In case of altimetry observations and FAC data, l is the number of grid cells for either the GIS or the AIS.

Here, we assume that the error covariance matrix for gravimetry observations \(C(\varvec{d}^{\textsc {grav}})\) can be identified with the inverse of the normal equations provided along with ITSG-Grace2018 (Mayer-Gürr et al. 2018) using the approach by Kvas et al. (2019) which includes background model uncertainties (Kvas and Mayer-Gürr 2019). We base the uncertainty information of the surface density rates on the mean covariance matrix of the monthly solutions over the period from Jan 2003 to Aug 2016. This averaging period avoids the months of exceptionally low quality solutions (Loomis et al. 2020). We assume no temporal correlations of GRACE monthly solution errors. In case of degree 1, we empirically estimate the covariance using an ensemble of degree-1 solutions and we ignore covariances between degree 1 and the other degrees. The SM (Sect. B) provides more details how we estimate \(C(\varvec{d}^{\textsc {grav}})\).

For altimetry observations, we retrieve the spatial covariance information (\(C(\varvec{d}^{\textsc {gis-\!\!alt}})\) and \(C(\varvec{d}^{\textsc {ais-\!\!alt}})\)) from an ensemble of surface elevation rates from CryoSat-2 data (from Jan 2011 to Dec 2019) for GIS and AIS. The ensemble has 140 members for both GIS and AIS, including solutions obtained by 7 retrackers (AWIICE2, EWIDTH, ICE1, ICE2, OCEAN, OCOG, TFMRA), 4 topographic fits, and 5 interpolation methods. To implement uncorrelated noise, we add a variance of (0.01 m a−1)2 to the diagonal of the covariance matrix, which is the median variance from the ensemble of surface elevation changes. The empirical error covariance thus obtained includes effects of temporal error correlations in the time series that underlie the 140 ensemble members of mean rates.

We characterize the uncertainty of FAC (\(C(\varvec{d}^{\textsc {gis-\!\!fac}})\) and \(C(\varvec{d}^{\textsc {ais-\!\!fac}})\)) similar to Willen et al. (2020): We approach the uncertainty of FAC by differences between two variants of FAC rates assuming that these differences express modelling errors. One variant is computed based on the RACMO2 SMB and the IMAU-FDM. The other variant is calculated using MAR SMB output from Fettweis et al. (2017) and Agosta et al. (2019) for GIS and AIS, respectively, and empirical relations between SMB variations and FAC variations established based on IMAU-FDM results (Willen et al. 2020). We calculate differences of the FAC rates between both variants over all 10 year time periods over the whole modelling period, i.e. we use a 10-year moving window with monthly increments. The time periods where SMB and FDM outputs are available are Jan 1960 to Dec 2015 and Jan 1979 to Dec 2016 for GIS and AIS, respectively, resulting in two ensembles of FAC rates with 553 (GIS) and 337 (AIS) members. Finally, the spatial covariance of each FAC rate is computed empirically using the ensembles. Similarly to the altimetry observations, we add a variance of (0.01 m a−1)2 to the diagonal of the covariance matrix. The empirical error covariance thus obtained includes the effect of temporal error correlations in the time series that underlie the ensemble members of mean rates.

Note that no FDM forced by MAR outputs is available. Therefore, our uncertainty characterization of FAC trends does not fully account for the uncertainty from firn modelling. Results by Verjans et al. (2021) for East Antarctica suggest that the uncertainty of firn model outputs is predominantly related to the uncertainty of their climate model inputs, rather than to uncertainties in the modelling of firn densification mechanisms.

We calculate the multivariate normal random vector \(\varvec{\epsilon }\), containing the random variables from the covariance information \(C(\varvec{d})\) assuming a multivariate normal distribution with an expectation vector of \(\varvec{0}\). To ensure reproducibility, we use the pseudorandom number generator Mersenne Twister (Matsumoto and Nishimura 1998) initialized with the same seed to compute a realization of \(\varvec{\epsilon }\), i.e. the errors \(\varvec{\varepsilon }\).

Table 1 Results from Experiments 1A, 2A, and 3A (E1A, E2A, E3A) that use the SELEN ICE-6G output as the synthetic GIA signal and results from Experiments 1B, 2B, and 3B (E1B, E2B, E3B) that use the GIA modelling output from Caron et al. (2018)
Full size table

3.5 Experimental setup

Here, our aim is to perform three kinds of experiments with two variants of synthetic observations (variants A and B). We base the observations of the variant A on the GIA output from SELEN run with ICE-6G ice loading history. This variant is consistent to the GIA parametrization (Sect. 3.2). Alternatively, we use the GIA modelling output from Caron et al. (2018) to compute the observations of the variant B (Sect. 3.3). In Experiment 1A (E1A) and Experiment 1B (E1B), observations contain no errors and we apply a weighting based on the full spatial covariance (Sect. 3.4). Thus, we demonstrate potential misattribution of signal as an error by using the covariance information. In Experiment 2A (E2A) and Experiment 2B (E2B), the observations contain correlated errors (Sect. 3.4) but during the estimation we pretend uncorrelated errors only. To do so, we apply a weighting matrix \(\varvec{{\tilde{P}}}\) which only contains the diagonal elements from \(\varvec{P}\) (Eq. 11). With this experiment we investigate whether real, possibly unknown correlations can be safely neglected in the inversion. In Experiment 3A (E3A) and Experiment 3B (E3B), the observations contain correlated errors and we involve the full covariance information during the parameter estimation.

To enable comparison of the results from the experiments, we calculate the root mean squares (RMS) of the signals. For example, for the synthetic true GIA-induced surface density rate in Antarctica, the RMS signal is

$$\begin{aligned} \mathrm{RMS}^{\mathrm{GIA}}_{\mathrm{AIS}} = \sqrt{ \frac{1}{v} \sum _{i=1}^{v} {({\dot{\kappa }}_{i}^{{\textsc {gia}}})}^{2}}. \end{aligned}$$
(22)

Further, we assess the results from the experiments by the misfit between the original signal and the estimated signal. For example, the RMS of the Antarctic GIA misfit is:

$$\begin{aligned} \Delta {\mathrm{RMS}^{\mathrm{GIA}}_{\mathrm{AIS}}} = \sqrt{ \frac{1}{v} \sum _{i=1}^{v} {({\dot{\kappa }}_{i}^{{\textsc {gia}}} - \hat{{\dot{\kappa }}}_{i}^{{\textsc {gia}}})}^{2}}. \end{aligned}$$
(23)

In case of GIA, we perform this integration over the GIS and AIS and include a buffer zone of 400 km around the area of the grounded ice sheet (Gunter et al. 2014) because the GIA signal is not limited to this area.

Moreover, we calculate the integrated mass and volume rates of the signals, e.g. for the synthetic true GIA and FAC signal in Antarctica,

$$\begin{aligned} {\dot{M}}^{{\textsc {gia}}}_{{\textsc {ais}}}&= \sum _{i=1}^{v} {\dot{\kappa }}_{i}^{{\textsc {gia}}} A_{i} \end{aligned}$$
(24)
$$\begin{aligned} {\dot{V}}^{{\textsc {fac}}}_{{\textsc {ais}}}&= \sum _{i=1}^{v} {\dot{h}}_{i}^{{\textsc {fac}}} A_{i} \end{aligned}$$
(25)

and the integrated misfit. For example for the Antarctic GIA and FAC this is

$$\begin{aligned} \Delta {\dot{M}}^{{\textsc {gia}}}_{{\textsc {ais}}}&= \sum _{i=1}^{v} ({\dot{\kappa }}_{i}^{{\textsc {gia}}} - \hat{{\dot{\kappa }}}_{i}^{{\textsc {gia}}}) A_{i} \end{aligned}$$
(26)
$$\begin{aligned} \Delta {\dot{V}}^{{\textsc {fac}}}_{{\textsc {ais}}}&= \sum _{i=1}^{v} ({\dot{h}}_{i}^{{\textsc {fac}}} - \hat{{\dot{h}}}_{i}^{{\textsc {fac}}}) A_{i}. \end{aligned}$$
(27)

4 Results

Table 1 presents the results of the experiments conducted with the two variants of observations (variants A and B) in context to the original signals (Sect. 3.3). We list RMS values (Eq. 22) and the integrated mass and volume changes (Eq. 24) of the original GIA, IMC, and FAC for the AIS and GIS. Additionally, we show the misfit in terms of \(\Delta \)RMS (Eq. 23) and the integrated misfit (Eq. 26) from each experiment. The ratio of the RMS of the misfit (RMS error) and the RMS of the signals indicates the relative noise level of the results. The ratio of the integrated difference and the integrated signals (\(|{\dot{M}}|\) ratio and \(|{\dot{V}}|\) ratio in Table 1) reveal the deviation of the results from the original signal. Figures 4, 5, 6 and S8–10 show maps of the estimated signals for GIS (a–c in each figure) and AIS (g–i in each figure), along with the misfit in Greenland (d–f in each figure) and in Antarctica (j–l in each figure). In Figure S11, we compare degree amplitudes of the original GIA signal, the Antarctic GIA signal, and the misfit from E2A and E3A.

In case of variant A experiments deviations of integrated results are only 6% at maximum (Table 1) in Greenland. Moreover, results from E1A and E3A in Greenland have only a small IMC and FAC misfit, reflected by small \(\Delta \)RMS values (Table 1); however, results from E2A have a noticeable misfit. The misfit is mainly present in coastal regions in addition to some random inland oscillations (Fig. 4e+f). For the results of the variant B experiments, these statements also generally apply to estimates of IMC and FAC in Greenland. In contrast, the deviations in the estimated GIA are very large. The RMS ratio is approximately 100% in all three variant B experiments. Note that the deviation ratio of integrated results is very large because the original integrated GIA effect from Caron et al. (2018) over Greenland is small (the original GIA effect is 11 \(\text {Gt a}^{-1}\) and the estimate from E3B is 25 \(\text {Gt a}^{-1}\)). In Antarctica deviations of integrated results are in the range of 3–11% in case of GIA and IMC from E1A, E1B, E3A, and E3B results (Table 1). The E2A and E2B results differ from the synthetic truth by 17% and 31%, respectively (integrated GIA signal) and by 20% and 49%, respectively (integrated IMC signal). FAC results in Antarctica deviate considerably from the synthetic truth. In E2A and E2B, the integrated FAC volume change of the AIS deviates most by − 15.2 km3a−1 and − 23.5 km3a−1, respectively, from the −10.0 km3a−1 true signal (Table 1). Note that the integrated FAC signal in Antarctica is relatively small compared to the other signals.

Despite the fact that E1A and E1B do not include any observational errors, the errors of retrieved signals from those experiments are not negligible. The \(\Delta \)RMS values are between one third and one half of the magnitude of \(\Delta \)RMS values from E3A and E3B for AIS GIA and AIS IMC. For GIS GIA and GIS IMC, E1A \(\Delta \)RMS is equal to E3A \(\Delta \)RMS and E1B \(\Delta \)RMS is equal to E3B \(\Delta \)RMS. Except for GIS GIA, the E3A/E3B results deviate less than the E2A/E2B results from the synthetic truth, in terms of both \(\Delta \)RMS values and integrated differences (Table 1). Notably, the RMS ratio of AIS GIA is 31% in E3A compared to 83% in E2A; and 51% in E3B compared to 111% in E2B. But also, for example, the RMS ratio of GIS IMC is 2% in E3A compared to 12% in E2A; and 8% in E3B compared to 12% in E2B. For Greenland, the misfit maps for IMC and FAC show a significant discrepancy for E2A/E2B (Fig. 4e+f, S10e+f), and somewhat less for E3B (Fig. 6). In Antarctica differential maps (Fig. 4j–l, 5j–l, S10j–l, and 6j–l) further illustrate that E3A/E3B results deviate less from the synthetic truth than E2A/E2B results. In Antarctica spatial correlations (Fig. 3j+k) are less present in E3A/E3B results than in E2A/E2B results. This is visible by IMC estimates from E2A/E2B (Fig. 4k, S10k) and E3 (Fig. 5k, 6k). The spatial patterns of the Antarctic GIA misfit (Fig. 4j, S10j) and the IMC misfit (Fig. 4k, S10k) are opposed to some degree.

The GIA signal we used for variant A observations is consistent to GIA parametrization with respect of their modelling environment. The integrated misfit of the GIA signal in Greenland is 1 \(\text {Gt a}^{-1}\) at maximum in all A experiments. Differences are small (Fig. 4d, 5d). Regarding the Antarctic GIA estimate, the misfit is considerably larger in E2A/E2B than in E3A/E3B (Fig. 5j, 6j, Fig. 4j, S10j), although typical GRACE error patterns are still visible for E3A/E3B. The E2A \(\Delta \)RMS of the Antarctic GIA signal is 7.4 kg m−2 a−1 (Table 1), which is close to the RMS of the original GIA signal of 8.9 kg m−2 a−1 (8.8 kg m−2 a−1 and 7.9 kg m−2 a−1 in case of E2B). When we consider the full spatial covariance information (E3A/E3B), the \(\Delta \)RMS decreases to 3.0 kg m−2 a−1/4.0 kg m−2 a−1. In the spectral domain, the GIA misfit of E2A and its excess over the GIA misfit of E3A are mainly present between degree 10 and 80 (Fig. S11a).

For the results from variant B experiments, we can summarize for the estimated GIA: In Greenland, the error of the GIA estimate from E1B–E3B is as large as the original GIA signal. Taking the spatial correlations into account does not improve the GIA result in Greenland. This is different in Antarctica where the integrated GIA misfit of the E3B result deviates by 5% from the original GIA signal which is close to the 8% deviation of the E3A result. However, the RMS ratio of the estimated GIA effect is larger for E3B than for E3A (51% vs. 31%). The error degree amplitudes of the estimated GIA (Fig. S6) are also larger for the E3B GIA result than for the E3A result in the degree range from 12 to 32. This is mainly due to the misfit of the variant B experiments outside Antarctica.

Fig. 4
figure 4

Results from Experiment 2A (E2A): estimated signals (a–c and g–i) and the difference to the original signals (d–f and j–l) for GIA-induced bedrock motion (first column), IMC-induced surface density change (second column), and FAC change (third column). The observations contain correlated errors and any correlations are neglected during the parameter estimation

Full size image
Fig. 5
figure 5

Results from Experiment 3A (E3A): estimated signals (a–c and g–i) and the difference to the original signals (d–f and j–l) of GIA-induced bedrock motion (first column), IMC-induced surface density change (second column), and FAC change (third column). The observations contain correlated errors, and the covariance information is used during the parameter estimation

Full size image
Fig. 6
figure 6

Results from Experiment 3B (E3B): estimated signals (a–c and g–i) and the difference to the original signals (d–f and j–l) for GIA-induced surface density change (first column), IMC-induced surface density change (second column), and FAC change (third column). The observations contain correlated errors and the covariance information is used during the parameter estimation

Full size image

5 Discussion

5.1 Conceptual assumptions

Six conceptual assumptions are paramount in our synthetic experiments.

  1. (1)

    We assume that we have full knowledge of observational uncertainties (Sect. 3.4). We compute the covariance information from real data and synthesize the errors from it. Thus, the weighting in the parameter estimation is consistent to the errors present in the synthetic observations. In reality, knowledge about uncertainties is incomplete so that the error characterization may deviate from the actual error characteristics.

  2. (2)

    We assume that altimetry observations are available with full spatial coverage. The orbit design (inclination) of altimetry missions and steep slope topography limit spatial sampling and lead to a polar gap and unobserved regions (e.g. valleys). In our experiments, we do not directly investigate effects due to sampling issues. However, we use the spread between the results of different interpolation methods in the altimetry ensemble to characterize errors in the altimetry products (Sect. 3.4).

  3. (3)

    We base the experiments on a period of 10 years. This is motivated by the period of availability of CryoSat-2 observations. For CryoSat-2, limitations addressed by point (2) are less severe than for other missions (Schröder et al. 2019). Obviously, errors in the calculated rates would be smaller over longer periods of time, with the restriction that correlated errors decrease less with a longer observation period than uncorrelated errors do. However, we do not quantify the error reduction with longer periods here, because analytical error models are not available and we estimate uncertainties empirically based on the chosen time period (Sect. 3.4).

  4. (4)

    In the synthetic experiments, we incorporate mean rates of IMC and FAC only. We did not yet generalize the approach to analyse interannual variations of IMC and FAC or to analyse time-variable rates of the ice dynamic contribution to the mass balance which are in particular present in the West Antarctic Ice Sheet (Willen et al. 2021).

  5. (5)

    We generate the GIA parametrization with the GIA modelling software SELEN (Spada and Melini 2019), which is publicly available. The modelling results generated with SELEN determine the relationship between GIA-induced gravity changes and geometry changes. We do not use an effective density to define the ratio of GIA-induced gravity change and the GIA-induced geometry change (e.g. Riva et al. 2009; Gunter et al. 2014; Engels et al. 2018). Furthermore, by the assumptions on generating the Antarctic GIA patterns (Sect. 3.2), we essentially specify a formal spatial GIA resolution of \(\sim \)250 km. Thus, the chosen Antarctic GIA parametrization can only hardly reproduce GIA changes at smaller spatial scales, e.g. as the GIA effect found by Barletta et al. (2018) (Fig. S5).

  6. (6)

    We do not investigate other signals in addition to IMC of ice sheets and GIA (\({\dot{\kappa }}^{{\textsc {other}}}\) in Eq. 3), e.g. terrestrial water redistributions, which we expect to be small over GIS and AIS.

5.2 Capabilities and limitations of the approach

In Greenland, we parametrize GIA with a single regional fingerprint which exactly matches the GIA signal to be estimated in terms of assumed ice history and rheology in variant A observations. Results from all experiments demonstrate that the estimate of the GIA signal in Greenland is robust against observational errors. This emphasizes that the fingerprint parametrization is a globally consistent and robust method. In addition, the relatively small magnitude of the integrated GIA signal in Greenland (Table 1) means that errors in the Greenland GIA recovery do not crucially affect the global inversion results. For example, Rietbroek et al. (2016) obtained a difference between the estimated Greenland fingerprint and the modelled Greenland fingerprint equivalent to only −0.003 mm a−1 global mean sea level. In general, the chosen parametrization strategy relies on knowledge of the ice history and the solid-Earth rheology. With the variant A experiments, we investigate the ideal case. With variant B simulated observations, we investigate the case when deviations between the modelled GIA fingerprints and the synthetic true GIA signal exist. We find that the fingerprint for Greenland created with SELEN and the ICE-6G glacial history restricted to Greenland is hardly able to resolve the present-day GIA effect predicted from Caron et al. (2018). Because the fingerprint can only be scaled as a whole, deviations affect the entire GIA signal represented by the fingerprint. This is especially problematic if the dominating spatial scale of errors in ice history and rheology are regional or local, as shown by Kappelsberger et al. (2021) and Adhikari et al. (2021). We confirm that large continental-scale fingerprints are inappropriate for the regional or local improvement of the GIA information.

In Antarctica, we apply a different strategy for the GIA parametrization, because we assume that spatial GIA patterns from geophysical modelling may have substantial errors (Sect. 1). The Antarctic GIA parametrization is consistent to geophysical GIA modelling by using the local deglaciation impulses to create the globally consistent GIA patterns, but remains independent from any full GIA modelling based on a prescribed glaciation history. This model-independent parametrization is less robust against observational errors. For degrees larger than 30, the effect of GRACE errors on the GIA retrieval is larger than the GIA signal itself (Fig. S6). If error covariances of the observations are not addressed (E2A and E2B), the integrated GIA signal will be still relatively close to the truth, but the noise level of the estimated signal will be similar to that of the signal itself (Table 1). In that case, the Antarctic GIA RMS error (\(\Delta \)RMS) is 83%/111% (E2A/E2B) of the RMS of the Antarctic GIA signal. This can be considerably improved by including the covariance information in the parameter estimation. In this case the RMS error is 31%/51% of the RMS signal (E3A/E3B). The incorporation of the full covariance information also improves the estimates for IMC and FAC. We thus caution that any real data analysis, using the localized GIA parametrization in a global inversion, will only provide meaningful results if the error covariance information is available and utilized.

The formal spatial resolution of our AIS GIA parametrization is determined by the spacing between the local deglaciation discs, that is, \(\sim \)250 km. This spacing is guided by the autocorrelation of the addressed GIA signal. To further justify our choice of spacing, we made GIA parametrization test experiments (Sect. A in the SM) and found that our parametrization recovers the ICE-6G(VM5a) GIA signal with only small misfits.

The effective spatial resolution of the AIS GIA retrieval may be assessed through comparing signal and error per spherical harmonic degree (Fig. S11a). For E3A, the amplitude of the Antarctic GIA signal exceeds the GIA error amplitude below degree 45, indicating an effective resolution of \(\sim \)450 km. Note that the GIA errors of the inversion are dominated by Antarctic GIA errors in the variant A experiments. This is different in variant B results, where the GIA misfit is dominated by misfits due to the incompatible fingerprints outside of Antarctica (Fig. S11b).

There are some degrees of freedom in the generation of the GIA patterns from deglaciation impulses. The shape of the response (Fig. 1) depends on the choice of the generic ice loading history and the assumed rheology. For example, shifting the time of the instantaneous deglaciation step further to the past (or to the present) would lead to wider (or, respectively, narrower) GIA patterns.

A present-day GIA signal resulting from ice loading changes during the last centuries and a comparatively low mantle viscosity, as the GIA signal Barletta et al. (2018) found in West Antarctica (Fig. S5), involves smaller spatial scales than the GIA signals predicted by, e.g. Caron et al. (2018). Other inversion frameworks aim to account for GIA signals resulting from the centennial ice loading changes and a low viscosity (Jiang et al. 2021), whereby their results show present-day GIA effects mainly on long spatial wavelengths (Fig. 7 in Jiang et al. (2021)). The smaller spatial scales of the modelled signal from Barletta et al. (2018) would require gravity fields with higher spatial resolution, preferably up to degree \(\sim \)200 (\(\sim \)100 km is the approximate half width of the found GIA feature). In that case, our approach could be adapted by using a localized GIA parametrization that captures the expected spatial scales. For this purpose, the time of the deglaciation impulse could be modified as well as the distance between the patterns and thus the number of parameters to be estimated. Likewise, the viscosity could be adjusted. Further test experiments with GIA models that include heterogeneity of the viscosity and ice loading history during the last centuries may help to find an appropriate GIA parametrization for a GIA signal on short spatial wavelengths. However, the applied parametrization strategy does not allow to invert for the glacial history or rheological parameters. Attributing the GIA signal inherent in satellite gravimetry observations to an ice history and rheological parameters is ambiguous and needs further boundary information.

We completely avoid filtering or regularization in the experiments and only apply the covariance information to account for errors. However, results from E1A and E1B (the error-free experiments) demonstrate that the incorporation of error correlations in the stochastic model may entail patterns of signal misattribution that are correspondingly correlated. That is, the separation of error patterns and signal patterns is imperfect. Besides, it should be noted that the uncertainty characterization we present here is an assumption on the observational covariance information based on available data sets.

Gunter et al. (2014) linked the surface density rate due to SMB and the firn thickness rate by a firn density (Eq. 7). This density is subject to large uncertainties (Willen et al. 2020), especially if the volume and mass rates are small and need further constraints. We link mass and volume changes by parametrizing FAC changes in addition to IMC. This allows to avoid the firn density (Eq. 7). FAC has the important advantage that it is linearly related to altimetry observations and can thus be directly implemented in the general linear model (Sect. 3.1) without linearization, as would be the case using a firn density.

By the study design, we neglect far-field effects due to hydrological or glacier mass changes (\({\dot{\kappa }}^{{\textsc {other}}}\) in Eq. 3), which is a limitation in our simulation setup and potentially leads to too optimistic results. We quantified the effect of mass changes originating outside of Antarctica and Greenland from Jan 2003 until Dec 2012 using a global inversion for all sea level contributions (Rietbroek et al. 2016; Uebbing et al. 2019). Hydrological mass changes have an integrated effect of 0.4 \(\text {Gt a}^{-1}\) and −1.0 \(\text {Gt a}^{-1}\) within in the grounding line of the GIS and AIS, respectively. Glacier mass changes have an effect of 1.4 \(\text {Gt a}^{-1}\) (GIS) and 10.5 \(\text {Gt a}^{-1}\) (AIS). We conclude that these effects are relatively small and justify neglecting them in this simulation study.

As discussed in Sect. 1, uncertainties of GIA forward models for the AIS are on the order of tens of \(\text {Gt a}^{-1}\) in terms of the integral mass effect. If GIA forward models are used to correct for GIA in GRACE IMC estimates, GIA model errors directly map (with opposite sign) into the IMC errors. For E3A and E3B, the AIS GIA error is below 10 \(\text {Gt a}^{-1}\) (Table 1), significantly lower than the uncertainty of GIA forward models. This low GIA error is reflected in an accordingly low IMC error for E3A and E3B. Its sign is opposite to that of the GIA error and is below 10 \(\text {Gt a}^{-1}\), too. Hence, the inversion is a promising approach to significantly reduce the uncertainty of GRACE AIS IMC inferences, previously related to GIA uncertainties.

5.3 Outlook

The next step will be obviously to implement the presented approach in a framework to process real-world data. The synthetic experiments demonstrate that the GIA parametrization presented here is appropriate to resolve GIA. In our ongoing research, we will incorporate the obtained findings into a global framework which is able to estimate all sea level contributions (Rietbroek et al. 2016; Uebbing et al. 2019). It will be investigated how the new GIA parametrization affects the GIA-related uncertainty in IMC and ocean mass change estimates and in sea level budget assessments under the conditions of the full global inversion.

We see potential for extending the approach by enabling the investigation of temporal variations of IMC and FAC rather than constant rates. For this purpose, the approach can be adapted so that time series with monthly resolution can be evaluated and, in line width Rietbroek et al. (2016), monthly IMC, monthly changes in FAC and a linear GIA effect can be estimated. However, this requires further investigation of the spatial and temporal covariance of both the involved signals and the observation errors.

Furthermore, real data results on the present-day GIA effect derived with the approach might hold some potential for investigation of the glacial history or lateral rheology heterogeneity. This might requires further development of the GIA patterns, i.e. the parametrization of GIA, beyond the 1-D rheology and the deglaciation impulses.

6 Conclusions

The inversion that we propose here uses a globally consistent parametrization of GIA and allows a co-estimation of GIA together with changes of the ice mass and the firn air content in Greenland and Antarctica. It enables to process, in a global framework, three types of observations available as five datasets: satellite gravimetry, satellite altimetry over GIS and AIS, as well as modelled firn air content over GIS and AIS in a single least-squares parameter estimation step. Loosening the dependence on geophysical GIA models of previous GIA parametrizations is paramount to our approach. The use of a set of ‘local GIA patterns’ (more precisely, global GIA patterns based on local deglaciation impulses) holds promise to spatially resolve GIA patterns that are not identified by geophysical GIA modelling and therefore not part of modelled regional GIA fingerprints.

In turn, a GIA parametrization through a large number of local GIA patterns is less robust and therefore more sensitive to the details of error covariance information of the input data. We assessed this covariance information from real observations of the five data sets and demonstrated that the set of GIA patterns is able to spatially resolve a physically meaningful present-day GIA effect in Antarctica that results from ICE-6G ice history and VM5a rheology. In this case the RMS error of the spatially resolved Antarctic GIA signal is about one third of the RMS of the GIA signal over an observation period of 10 years assuming ideal observing conditions and full knowledge of the covariance information. This RMS error increases up to half of the RMS of the GIA signal in Antarctica when we aim to resolve the GIA signal predicted by an alternative GIA model. Longer observation periods would lead to smaller errors of the mean rate, which we do not quantify here, because we characterize errors empirically over the 10-year observation period. From the experiments we conclude: If errors of the input data sets are thoroughly characterized, a GIA parametrization by local GIA patterns can plausibly resolve the GIA-induced deformation from satellite observations in a global framework. On the other hand, if the error covariances are unknown, error and signal cannot be clearly distinguished in the GIA result. In this feasibility study, we limit the investigations to one realization of the GIA parametrization. As a caveat, we neglect for hydrological and glacier mass changes outside of the ice sheets in our simulation study, but which need to be accounted for when evaluating real world data. However, global inversion results according to Rietbroek et al. (2016); Uebbing et al. (2019) show rather small far-field effects over ice sheets.