Periodic portfolio revision with transaction costs

Abstract

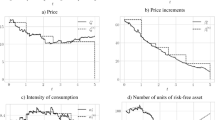
In this paper we consider the impact of transaction costs on the periodic portfolio revision. We offer a statistical model for simulation of daily returns which can explain the empirical behavior of equity returns. The model is based on ARMA–GARCH processes, principal component analysis, classical tempered stable distribution, and skewed $t$ copula. The main contribution of this paper is the application of a new approach for modelling transaction costs using daily returns by estimating an optimal portfolio with an arbitrary length for the holding period. Moreover, we compare the portfolio selection problem solved with and without transaction costs by applying different risk and performance measures on simulated returns, taking into account their Sharpe ratio and stable tail-adjusted return ratio. The experimental analysis suggests that the incorporation of transaction costs into an optimal portfolio framework leads to remarkable reduction of the transaction costs and stabilization of the optimal portfolio strategy. However, ignoring transaction costs does not always result in a less efficient portfolio.

Appendix

1.1 CTS distribution

The tempered stable random variables do not have a closed form of a probability density function, but they are defined by their characteristic function. For $\alpha \in (0, 2), \, C, \, \lambda _+, \, \lambda _- > 0$, and $m \in {\mathbb {R}}$. $X$ is said to have classical tempered stable distribution, if the characteristic function of $X$ is given by

$$\begin{aligned} \phi _X(u)= & {} \phi _{\textit{CTS}}(u; \alpha , C, \lambda _+, \lambda _-, m) \\= & {} \exp \biggl ( i u m - i u C \varGamma (1-\alpha ) (\lambda _+^{\alpha -1} - \lambda _-^{\alpha -1} ) \\&\quad +\,C \varGamma (-\alpha ) \bigl ( (\lambda _+ - i u)^{\alpha } -\lambda _+^{\alpha } +(\lambda _- + iu)^{\alpha } -\lambda _-^{\alpha } \bigl ) \biggl ), \end{aligned}$$

where $X \sim CTS(\alpha , C, \lambda _+, \lambda _-, m)$. A Lévy process induced from the CTS distribution is called a classical tempered stable process with parameters $(\alpha , C, \lambda _+, \lambda _-, m)$.

The parameters $\lambda _+$ and $\lambda _-$ give the rate of tail decay on the positive and negative part, respectively. If $\lambda _+ > \lambda _-$, the distribution is skewed to the left and vice versa, and if $\lambda _+=\lambda _-$, then it is symmetric. The parameter $\alpha$ describes the tail weight and $C$ determines the arrival rate of jumps of given size.

The following substitution supposed by Kim et al. (2010b)

$$\begin{aligned} C= & {} \biggl (\varGamma (2- \alpha ) (\lambda _+^{\alpha -2} + \lambda _-^{\alpha -2}) \biggl )^{-1},\\ m= & {} 0, \end{aligned}$$

leads to $X \sim CTS(\alpha , C, \lambda _+, \lambda _-, 0)$, where the random variable $X$ has a zero mean and unit variance, and is called the standard CTS distribution with parameters $(\alpha , \, \lambda _+, \, \lambda _-)$ and is denoted by $X \sim$ stdCTS$(\alpha , \lambda _+, \lambda _-)$.

In the empirical part of this study we apply the following interesting results, for the CTS distribution derived by Kim et al. (2010a). They give a closed-form solution for the cumulative distribution function $F_{{X}}$ of $X$ and for the survival function $\overline{F}_{{X}}$ of $X$

$$\begin{aligned} F_{{X}}(x) ={e^{x \rho } \over \pi } \mathfrak {R}\biggl ( \int _{0}^{\infty } e^{-x u} {\phi _X(u + i \rho ) \over \rho - u i }du \biggl ), \quad \text {for} \, x \in {\mathbb {R}}, \end{aligned}$$

where $\rho >0$, such that $|\phi _X (z)|<0$, $\forall \, z \in {\mathbb {C}}$, with $\mathfrak {I}(z)=\rho ,$

$$\begin{aligned} \overline{F}_{{X}}(x) ={e^{x \rho } \over \pi } \mathfrak {R}\biggl ( \int _{0}^{\infty } e^{-x u} {\phi _X(u + i \rho ) \over u i -\rho }du \biggl ), \quad \text {for} \, x \in {\mathbb {R}}, \end{aligned}$$

where $\rho <0$, such that $|\phi _X (z)|<0$, $\forall \, z \in {\mathbb {C}}$, with $\mathfrak {I}(z)=\rho$.

The probability density function is given through the inverse Fourier transform

$$\begin{aligned} f_X(x)= {1 \over 2 \pi } \int _{-\infty }^{\infty } e^{- i u x} \phi _x(u)du. \end{aligned}$$

1.2 Principal component analysis

Principal component analysis (PCA) is a technique which simplifies a data set. It was first introduced by Pearson (1901) and Hotelling (1933), while the best modern reference is Jolliffe (2002). The application of the method reduces the dimensionality of multivariate data whilst preserving as much of the relevant information as possible. PCA is a model that reveals the internal structure of the data in a way that best explains its variance. Mathematically, it is defined as an orthogonal linear transformation that transforms the data to a new coordinate system such that the new set of variables, the principal components (PCs), are linear functions of the original variables and are uncorrelated, and the greatest variance by any projection of the data comes to lie on the first coordinate, the second greatest variance on the second coordinate, and so on.

Hence, $n$ original correlated time series $y_i$ can be replaced with $n$ uncorrelated time series $F_j$ assuming that each $y_i$ is a linear combination of $F_j$. Then, the dimensionality reduction is done by choosing only the first $m$ factors, whose variance is significantly different from zero. Thus, each series $y_i$ can be approximated as a linear combination of the factors plus small uncorrelated noise

$$\begin{aligned} y_i=\sum _{j=1}^{m}\beta _{i,j} F_j + \sum _{j=m+1}^{n}\beta _{i,j} F_j =\sum _{j=1}^{m}\beta _{i,j} F_j + \epsilon _i, \end{aligned}$$

where $i=1 \ldots n$, and $n$ is the number of stocks. Generally, the principal component analysis can be applied either to the variance–covariance matrix or to the correlation matrix.

1.3 Skewed $t$ copula

A multivariate function $C$ on $[0, 1]^m$ is called an $m$-dimensional copula function, if it is a distribution function with standard uniform marginal distributions on [0,1]. According to Sklar’s Theorem (1959) and Nelsen (2006) every cumulative density function $F$ with marginal distributions $F_1,\ldots , F_m$ can be written as

$$\begin{aligned} F(x_1, \ldots , x_m) = C\bigl (F_1(x_1), \ldots , F_d(x_m) \bigl ), \end{aligned}$$

(14)

where $C$ is a copula function, which is uniquely determined on $[0, 1]^m$ for distributions $F$ with absolutely continuous margins. Any copula $C$ can be employed to join a collection of univariate cumulative density functions $F_1,\ldots , F_m$, so we can achieve a multivariate cumulative density function $F$ with margins $F_1,\ldots , F_m$. For strictly increasing continuous marginals the copula $C$ of their joint distribution function can be extracted from (14) by evaluating

$$\begin{aligned} C(u) := C(u_1,\ldots , u_m) = F(F_1^{-1} (u_1), \ldots , F^{-1}_m (u_m)), \end{aligned}$$

(15)

where the $F^{-1}_i$ are the quantile functions of the marginals. The form of the multivariate skewed Student’s $t$ distribution, which we apply is defined through the following stochastic representation supposed by Dematra and McNeil (2005),

$$\begin{aligned} X=\mu + \gamma W + \sqrt{W}Z, \end{aligned}$$

(16)

where $W \in$ IG$(\nu /2, \nu /2)$ and $Z \in N(0,\varSigma )$ and $Z$ is independent of $W$, $\gamma =(\gamma _1,\ldots , \gamma _m)$ is an $m$-dimensional vector accounting for the skewness, $\mu =(\mu _1,\ldots , \mu _m)$ is an $m$-dimensional location parameter vector, and $\nu$ is the degrees of freedom. We denote this distribution by $X \sim t_m(\nu ,\mu ,\varSigma ,\gamma )$, where its marginal distribution is given through $X_i \sim t_1(\nu , \mu _i,\varSigma _{ii}, \gamma _{i})$. The notation $IG(\nu /2, \nu /2)$ stands for the inverse gamma distribution with parameters $\nu /2$. Thus, $W$ is a one-dimensional random variable and $Z$ is a random vector having a zero-mean multivariate normal distribution with covariance matrix

$$\begin{aligned} \varSigma = \begin{pmatrix} \sigma _{11} &{}\quad \sigma _{12}&{}\quad \cdots &{}\quad \sigma _{1m} \\ \sigma _{21} &{}\quad \sigma _{22}&{}\quad \cdots &{}\quad \sigma _{2m} \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ \sigma _{m1} &{}\quad \sigma _{m2} &{}\quad \cdots &{}\quad \sigma _{mm} \end{pmatrix} \end{aligned}$$

The multivariate skewed Student’s $t$ distribution has a closed density, which is given through

$$\begin{aligned} f_X(x)={ c K_{(\nu +n)/2} \biggl ( \sqrt{ \bigl ( \nu + (x-\mu )'\varSigma ^{-1}(x-\mu )\gamma '\varSigma ^{-1} \gamma \bigl ) } \biggl ) \text {exp}\bigl ( (x-\mu )'\varSigma ^{-1} \gamma \bigl ) \over \bigl ( \sqrt{\nu + (x-\mu )'\varSigma ^{-1}(x-\mu )\gamma '\varSigma ^{-1} \gamma } \bigl )^{-{\nu +n\over 2 } } \left( 1 + {(x-\mu )'\varSigma ^{-1}(x-\mu ) \over \nu } \right) ^{{\nu +n\over n } } } \end{aligned}$$

where $x \in {\mathbb {R}}^n$, $K$ is the modified Bessel function of the third kind, and $c$ is the normalizing constant

$$\begin{aligned} c= { 2 ^{2- (v+d) \over 2 } \over \varGamma ({\nu \over 2 }) (\pi \nu )^{d/2}|\varSigma |^{1/2}}. \end{aligned}$$

The copula remains invariant under a standardization of the marginal distributions and any series of strictly increasing transformations. Thus, it follows that the copula of a $t_m( \nu , \mu ,\varSigma , \gamma )$ is identical to that of $t_m(\nu , 0, P, \gamma )$ distribution, where $P$ is the correlation matrix implied by the covariance matrix $\varSigma$ and we denote it by $C^{t}_{\nu , P, \gamma }$,

$$\begin{aligned}&C^{t}_{\nu , P, \gamma }(u)\\&\quad = \int _{-\infty }^{t_{\nu ,\gamma }^{-1}(u_m)} \cdots \int _{-\infty }^{t_{\nu ,\gamma }^{-1}(u_1)} { c K_{(\nu +n)/2} \biggl ( \sqrt{ \bigl ( \nu + x'P^{-1}x \gamma 'P^{-1} \gamma \bigl ) } \biggl ) \text {exp}(x'P^{-1} \gamma ) \over \bigl ( \sqrt{\nu + x'P^{-1}x \gamma 'P^{-1} \gamma } \bigl )^{-{\nu +n\over 2 }} \left( 1 + {x'P^{-1}x \over \nu } \right) ^{{\nu +n\over n }}}dx, \end{aligned}$$

where $t_{\nu ,\gamma }^{-1}$ denotes the quantile function of a skewed univariate $t$ distribution. By calibration of the skewed $t$ copula we use its density function, which can be derived from (15) and it has the form

$$\begin{aligned} c^t_{\nu , P, \gamma }(u) ={f_{\nu , P, \gamma }(t^{-1}_{\nu , \gamma } (u_1), \ldots , t^{-1}_{\nu , \gamma } (u_m)) \over \Pi _{i=1}^m f_{\nu , \gamma } \bigl ( t^{-1}_{\nu , \gamma } (u_i) \bigl )}, \qquad u \in (0,1)^m, \end{aligned}$$

(17)

where $f_{\nu , P, \gamma }$ is the joint density of a $t_m(\nu ,0,1, \gamma )$ and $f_{\nu ,\gamma }$ is the density of the univariate skewed standard $t$-distribution with $\nu$ degrees of freedom and parameter of skewness $\gamma$.

1.4 Risk measures

1.4.1 VaR

VaR, or a value-at-risk, is a risk measure (see for details Duffie and Pan 1997; Jorion 2006) that was accepted in nineties in the financial industry. VaR is defined as the minimum level of loss at a given, significantly high confidence for a predefined time horizon. For the sake of simplicity, we take 1 day as the time horizon in the following example.

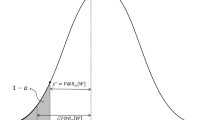
VaR at confidence level $(1-\epsilon )100\,\%$ of a random variable $X$, which describes random returns, is defined as the negative of the lower $\epsilon$-quantile of the return distribution

$$\begin{aligned} \text {VaR}_\epsilon (X)= - \inf _x \{ x \, | P(X \le x) \ge \epsilon \} =- F_X^{-1}(\epsilon ), \end{aligned}$$

(18)

where $\epsilon \in (0,1)$ and $F^{-1}_X(\epsilon )$ is the inverse of the cumulative distribution function.

The following two important properties are important when dealing with VaR

$$\begin{aligned} \text {VaR}_\epsilon (X+C)= & {} \text {VaR}_\epsilon (X) -C,\\ \text {VaR}_\epsilon (\lambda X)= & {} \lambda \text {VaR}_\epsilon (X). \end{aligned}$$

For the non-parametric estimate of VaR no assumptions for the distributional returns are needed and VaR at confidence level $(1-\epsilon )100\,\%$ is given by

$$\begin{aligned} \widehat{\text {VaR}}_\epsilon (x)= - x_{(\lceil n \epsilon \rceil )}, \end{aligned}$$

where $\lceil y \rceil$ is the smallest integer larger than $y$ and $x$ is the sorted vector of observations and $n$ is the size of the sample. The sorted sample is presented as follows $x_{(1)} \le x_{(2)} \le , \ldots , \le x_{(n)}$, thus $x_{(1)}$ is the smallest observation in the sample and $x_{(n)}$ is the largest.

1.4.2 AVaR

The average value-at-risk (AVaR) is the average of VaRs larger than the VaR for a given tail probability. It is a risk measure that is a superior alternative to VaR, because it satisfies all axioms of coherent risk measures (Acerbi and Tasche 2001).

The AVaR at tail probability $\epsilon$ of a random variable $X$, which describes random returns, is computed through

$$\begin{aligned} \text {AVaR}_\epsilon (X)= {1 \over \epsilon } \int _{0}^{\epsilon } \text {VaR}_p (X) dp, \end{aligned}$$

where VaR$_p$ is defined in Eq. (18).

For the non-parametric estimation of AVaR at tail probability $\epsilon$, no distributional assumptions are needed for the sample. Rockafellar and Uryasev (2002) suppose the following formula

$$\begin{aligned} \widehat{\text {AVaR}}_\epsilon (x)=-{1 \over \epsilon } \left( {1 \over n} \sum _{k=1}^{ \lceil n \epsilon \rceil -1 } x_k + \left( \epsilon -{ \lceil n \epsilon \rceil -1 \over n } x_{(\lceil n \epsilon \rceil )} \right) \right) , \end{aligned}$$

where $\lceil y \rceil$ is the smallest integer larger than $y$ and $x$ is the sorted vector of observations and $n$ is the size of the sample. The sorted sample is presented as follows $x_{(1)} \le x_{(2)} \le , \ldots , \le x_{(n)}$, thus $x_{(1)}$ is the smallest observation in the sample and $x_{(n)}$ is the largest.

1.5 Performance measures

1.5.1 Sharpe ratio

Sharpe (1966) ratio calculates the adjusted return of the portfolio relative to a target return. It is the ratio between the average active portfolio return and its standard deviation. In this case, it can be thought of as a reward to a variability ratio. Commonly, it is defined as

$$\begin{aligned} {\textit{SR}}(w)={ E(r_p -r_b) \over \sigma (r_p -r_b) }, \end{aligned}$$

when the benchmark return is a random variable. If it is a constant, then the Sharpe ratio is equal to

$$\begin{aligned} {\textit{SR}}(w)={ w'\mu -r_b \over \sigma _{r_p} }. \end{aligned}$$

1.5.2 STARR

STARR (stable tail-adjusted return ratio) is an alternative performance measure that overcomes the disadvantages of the Sharpe ratio, selecting AVaR as a risk measure Rachev et al. (2008). It is defined as

$$\begin{aligned} {\textit{STARR}}_\epsilon (w)={ E(r_p -r_b) \over \text {AVaR}_{\epsilon }(r_p -r_b) }. \end{aligned}$$

If $r_b$ is a constant benchmark return, then STARR is equal to

$$\begin{aligned} {\textit{STARR}}_\epsilon (w)={ w'\mu -r_b \over \text {AVaR}_{\epsilon }(r_p) +r_b }. \end{aligned}$$

In this research, we use the tail probability $\epsilon =1\,\%$ for computing the STARR.

1.5.3 Rachev ratio

The Rachev ratio Biglova et al. (2004) is a performance measure that is constructed on the basis of AVaR. The reward measure is defined as the average of the quantiles of the portfolio return distribution which are above a certain quantile level or expected tail gain, and the risk measure is the AVaR, expected tail loss, at a given tail probability. The Rachev ratio is defined in the following way

$$\begin{aligned} {\textit{RR}}_{\epsilon _1,\epsilon _2} (w)={ \text {AVaR}_{\epsilon _1}( r_b-r_p) \over \text {AVaR}_{\epsilon _2}(r_p -r_b)}, \end{aligned}$$

where the tail probability $\epsilon _1$ denotes the quantile level of the reward measure and $\epsilon _2$ is the tail probability of the AVaR. For the computation of the Rachev ratio we utilize $\epsilon _1=1\,\%$ and $\epsilon _2=1\,\%$.