A test of linearity in partial functional linear regression

Abstract

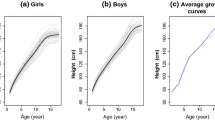
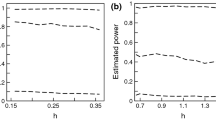
This paper investigates the hypothesis test of the parametric component in partial functional linear regression. We propose a test procedure based on the residual sums of squares under the null and alternative hypothesis, and establish the asymptotic properties of the resulting test. A simulation study shows that the proposed test procedure has good size and power with finite sample sizes. Finally, we present an illustration through fitting the Berkeley growth data with a partial functional linear regression model and testing the effect of gender on the height of kids.

Appendix

In order to provide the proofs of the theorems, we first define the notation and give preliminary results.

Write ${\hat{V}}_k(g)=\sum _{j=1}^m\frac{\langle {\hat{C}}_{z_kX},{\hat{v}}_j\rangle \langle {\hat{v}}_j,g\rangle }{{\hat{\lambda }}_j}$, $V_k(g)=\sum _{j=1}^{\infty }\frac{\langle C_{z_kX},v_j\rangle \langle v_j,g\rangle }{\lambda _j}$ for $g\in L^2[0,1]$, $\hat{{\varvec{B}}}={\hat{C}}_{{\varvec{z}}}-\{{\hat{V}}_k({\hat{C}}_{z_{l}X})\}_{k,l=1,\ldots ,p}$. Then it is easy to show that ${\varvec{B}}$ defined in Assumption 6 can be expressed as ${\varvec{B}}=C_{{\varvec{z}}}-\{{V_k(C_{z_{l}X})}\}_{k,l=1,\ldots ,p}$, and that $\hat{{\varvec{B}}}=\frac{1}{n}{\varvec{Z}}^T({\varvec{I}}-{\varvec{S}}_m){\varvec{Z}}$ if ${\hat{\lambda }}_1>\cdots>{\hat{\lambda }}_n>0$ holds. Furthermore, we have Lemma 1.

Lemma 1

Suppose Assumptions 1–6 hold. Then, one has

$$\begin{aligned} \hat{{\varvec{B}}}-\frac{1}{n}{\varvec{Z}}^T({\varvec{I}}-{\varvec{S}}_m){\varvec{Z}}\overset{p}{\longrightarrow }0, \ \ \hat{{\varvec{B}}}\overset{p}{\longrightarrow }{\varvec{B}}, \quad {\text{ as } \ \ n \rightarrow \infty }. \end{aligned}$$

(11)

Proof

This is a straightforward corollary of Theorem 3.1 in Shin (2009).

Lemma 2

If $H_0$ and Assumptions 1–3 hold, then

$$\begin{aligned} \frac{1}{n}{\text {RSS}}(H_0)\overset{p}{\longrightarrow }\sigma ^2,\;\text {as}\ n \rightarrow \infty . \end{aligned}$$

(12)

Proof

Let vector ${\varvec{U}}_{mi}$ be the ith row of matrix ${\varvec{U}}_m$, then

$$\begin{aligned} \frac{1}{n}{\text{ RSS }}(H_0)= & {} \frac{1}{n}\sum _{i=1}^n(Y_i-{\varvec{U}}_{mi}{\hat{\gamma }}_0)^2\nonumber \\= & {} \frac{1}{n}\sum _{i=1}^n\left( \epsilon _i+\int ^{1}_{0}\gamma (t)X_i(t)dt-{\varvec{U}}_{mi}{\hat{\gamma }}_0\right) ^2\nonumber \\= & {} \frac{1}{n}\sum _{i=1}^n\epsilon _i^2+\frac{1}{n}\sum _{i=1}^n\left( \int ^{1}_{0}\gamma (t)X_i(t)dt- {\varvec{U}}_{mi}{\hat{\gamma }}_0\right) ^2\\&+ \frac{2}{n}\sum _{i=1}^n\epsilon _i\left( \int ^{1}_{0}\gamma (t)X_i(t)dt-U_{mi}{\hat{\gamma }}_0\right) \end{aligned}$$

Using the law of large numbers, we get

$$\begin{aligned} \frac{1}{n}\sum _{i=1}^n\epsilon _i^2\overset{p}{\longrightarrow }\sigma ^2. \end{aligned}$$

By the Cauchy-Schwarz inequality and Theorem 1 in Hall and Horowitz (2007), we therefore have

$$\begin{aligned}&\frac{1}{n}\sum _{i=1}^n\left( \int ^{1}_{0}X_i(t)(\gamma (t)-{\hat{\gamma }}_0(t))dt\right) ^2\\&\quad \le \frac{1}{n}\sum _{i=1}^n\int ^{1}_{0}\big (X_i(t)\big )^2dt\int ^{1}_{0}\big (\gamma (t)-{\hat{\gamma }}_0(t)\big )^2dt=o_p(1). \end{aligned}$$

Similarly, it holds

$$\begin{aligned} \frac{2}{n}\sum _{i=1}^n\epsilon _i\left( \int ^{1}_{0}\gamma (t)X_i(t)dt-U_{mi}{\hat{\gamma }}_0\right) =o_p(1). \end{aligned}$$

This completes the proof of Lemma 2. $\square$

Proof of Theorem 1

Firstly, according to $\hat{\varvec{\beta }}_1=({\varvec{Z}}^T({\varvec{I}}-{\varvec{S}}_m){\varvec{Z}})^{-1}{\varvec{Z}}^T({\varvec{I}}-{\varvec{S}}_m){\varvec{Y}}$, one has

$$\begin{aligned} {\varvec{Z}}^T({\varvec{I}}-{\varvec{S}}_m){\varvec{Y}}=({\varvec{Z}}^T({\varvec{I}}-{\varvec{S}}_m){\varvec{Z}})\hat{\varvec{\beta }_1}. \end{aligned}$$

Furthermore it is easy to get

$$\begin{aligned} {\varvec{U}}_m(\hat{{\widetilde{\varvec{\gamma }}}}_0-\hat{{\widetilde{\varvec{\gamma }}}}_1)&={\varvec{S}}_m{\varvec{Z}}\hat{\varvec{\beta }}_1,\\ {\varvec{U}}_m(\hat{{\widetilde{\varvec{\gamma }}}}_0+\hat{{\widetilde{\varvec{\gamma }}}}_1)&={\varvec{S}}_m(2{\varvec{Y}}-{\varvec{Z}}\hat{\varvec{\beta }}_1). \end{aligned}$$

Then

$$\begin{aligned}&{\text{ RSS }}(H_0)-{\text{ RSS }}(H_A)\nonumber \\&\quad =({\varvec{Z}}\hat{\varvec{\beta }}_1+{\varvec{U}}_m\hat{{\widetilde{\varvec{\gamma }}}}_1- {\varvec{U}}_m\hat{{\widetilde{\varvec{\gamma }}}}_0)^T(2{\varvec{Y}}-{\varvec{U}}_m \hat{{\widetilde{\varvec{\gamma }}}}_0-{\varvec{U}}_m\hat{{\widetilde{\varvec{\gamma }}}}_1-{\varvec{Z}}\hat{\varvec{\beta }}_1)\\&\quad =({\varvec{Z}}\hat{\varvec{\beta }}_1-{\varvec{S}}_m{\varvec{Z}}\hat{\varvec{\beta }}_1)^T [({\varvec{I}}-{\varvec{S}}_m)(2{\varvec{Y}}-{\varvec{Z}}\hat{\varvec{\beta }}_1)]\\&\quad =\hat{\varvec{\beta }}_1^T({\varvec{Z}}^T{\varvec{Z}}-{\varvec{Z}}^T{\varvec{S}}_m{\varvec{Z}})\hat{\varvec{\beta }}_1\\&\quad = n\hat{\varvec{\beta }}_1^T\left( {\hat{C}}_{{\varvec{z}}}- \sum _{j=1}^m\frac{\langle {\hat{C}}_{{\varvec{z}}X},{\hat{v}}_j\rangle \langle {\hat{C}}_{X{\varvec{z}}},{\hat{v}}_j\rangle }{{\hat{\lambda }}_j}\right) \hat{\varvec{\beta }}_1\\&\quad =n\hat{\varvec{\beta }}_1^T\hat{{\varvec{B}}}\hat{\varvec{\beta }}_1. \end{aligned}$$

Following from Theorem 3.1 in Shin (2009), one has

$$\begin{aligned} \sqrt{n}\hat{\varvec{\beta }}_1\overset{d}{\longrightarrow } N(0,\sigma ^2{\varvec{B}}^{-1}). \end{aligned}$$

Combining this with Lemma 1 and Lemma 2, we can obtain Theorem 1. $\square$

Proof of Theorem 2

Theorem 3.1 in Shin (2009) and Lemma 2 imply that

$$\begin{aligned}&\frac{1}{n}\big \{{\text{ RSS }}(H_0)-{\text{ RSS }}(H_A)\big \}\nonumber \\&\quad =\hat{\varvec{\beta }}_1^T{{\varvec{B}}}\hat{\varvec{\beta }}_1+o_p(1).\\&\quad =\big \{{\varvec{\beta }}+O_p(n^{-1/2})\big \}^T{{\varvec{B}}}\big \{{\varvec{\beta }}+ O_p(n^{-1/2})\big \}+o_p(1)\\&\quad ={\varvec{\beta }}^T{{\varvec{B}}}{\varvec{\beta }}+o_p(1). \end{aligned}$$

Setting ${\varvec{V}}=[\langle X_1,\gamma \rangle ,\ldots ,\langle X_n,\gamma \rangle ]^T$, under the alternative hypothesis,

$$\begin{aligned}&\frac{1}{n}{\text{ RSS }}(H_0)=\frac{1}{n}{\varvec{Y}}^T({\varvec{I}}-{\varvec{S}}_m){\varvec{Y}}\\&\quad =\frac{1}{n}({\varvec{Z}}\varvec{\beta }+{\varvec{V}}+\varvec{\varepsilon })^T ({\varvec{I}}-{\varvec{S}}_m)({\varvec{Z}}\varvec{\beta }+{\varvec{V}}+\varvec{\varepsilon })\\&\quad =\frac{1}{n}({\varvec{Z}}\varvec{\beta })^T({\varvec{I}}-{\varvec{S}}_m)({\varvec{Z}}\varvec{\beta })+\frac{1}{n}{\varvec{V}}^T ({\varvec{I}}-{\varvec{S}}_m){\varvec{V}}+\frac{1}{n} \varvec{\varepsilon }^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }\\&\qquad +\frac{2}{n}({\varvec{Z}}\varvec{\beta })^T({\varvec{I}}-{\varvec{S}}_m) \varvec{\varepsilon }+\frac{2}{n}({\varvec{Z}}\varvec{\beta })^T({\varvec{I}}-{\varvec{S}}_m){\varvec{V}} +\frac{2}{n}{\varvec{V}}^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }. \end{aligned}$$

First applying Lemma 1 we conclude that

$$\begin{aligned} \frac{1}{n}({\varvec{Z}}\varvec{\beta })^T({\varvec{I}}-{\varvec{S}}_m)({\varvec{Z}}\varvec{\beta }) ={\varvec{\beta }}^T{{\varvec{B}}}{\varvec{\beta }}+o_p(1). \end{aligned}$$

(13)

By routine calculation, one has

$$\begin{aligned} \text {E}\left\{ \frac{1}{n}\varvec{\varepsilon }^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }\right\} =\frac{(n-m)\sigma ^2}{n}=\sigma ^2+o(1),\\ \end{aligned}$$

and

$$\begin{aligned} \text {Var}\left\{ \frac{1}{n}\varvec{\varepsilon }^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }\right\} =O\left( {m\over n}\right) . \end{aligned}$$

Thus it holds that

$$\begin{aligned} \frac{1}{n}\varvec{\varepsilon }^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }=\sigma ^2+o_p(1). \end{aligned}$$

(14)

Notice that

$$\begin{aligned} \frac{1}{n}{\varvec{V}}^T{\varvec{V}}= & {} \frac{1}{n}\sum _{i=1}^n\langle X_i,\gamma \rangle ^2\\= & {} \frac{1}{n}\sum _{i=1}^n\int ^{1}_{0}\int ^{1}_{0}X_i(t)X_i(s)\gamma (t)\gamma (s)dtds\\= & {} \int ^{1}_{0}\int ^{1}_{0}{\hat{C}}_X(t,s)\gamma (t)\gamma (s)dtds. \end{aligned}$$

Applying the orthogonality of ${\hat{v}}_i$, one has

$$\begin{aligned}&\frac{1}{n}{\varvec{V}}^T{\varvec{S}}_m {\varvec{V}} \\&\quad =\frac{1}{n}\left\{ \sum _{l=1}^n\langle X_l,\gamma \rangle \sum _{k=1}^m\frac{1}{n{\hat{\lambda }}_k}\langle X_l,{\hat{v}}_k\rangle \langle X_1,{\hat{v}}_k\rangle ,\ldots ,\right. \\&\left. \qquad \qquad \sum _{l=1}^n\langle X_l,\gamma \rangle \sum _{k=1}^m\frac{1}{n{\hat{\lambda }}_k}\langle X_l,{\hat{v}}_k\rangle \langle X_n,{\hat{v}}_k\rangle \right\} {\varvec{V}}\\&\quad =\frac{1}{n}\sum _{h=1}^n\sum _{l=1}^n\langle X_l,\gamma \rangle \sum _{k=1}^m \frac{1}{n{\hat{\lambda }}_k} \langle X_l,{\hat{v}}_k\rangle \langle X_h,{\hat{v}}_k\rangle \langle X_h,\gamma \rangle \\&\quad =\frac{1}{n}\sum _{l=1}^n\langle X_l,\gamma \rangle \sum _{k=1}^m \frac{1}{n{\hat{\lambda }}_k}\langle X_l,{\hat{v}}_k\rangle \sum _{h=1}^n\langle X_h,{\hat{v}}_k\rangle \langle X_h,\gamma \rangle \\&\quad =\frac{1}{n}\sum _{l=1}^n\langle X_l,\gamma \rangle \sum _{k=1}^m \frac{1}{{\hat{\lambda }}_k}\langle X_l,{\hat{v}}_k\rangle \langle {\hat{C}}_X{\hat{v}}_k,\gamma \rangle \\&\quad =\frac{1}{n}\sum _{l=1}^n\langle X_l,\gamma \rangle \sum _{k=1}^n\langle X_l,{\hat{v}}_k \rangle \langle {\hat{v}}_k,\gamma \rangle -\frac{1}{n}\sum _{l=1}^n\langle X_l,\gamma \rangle \sum _{k=m+1}^n\langle X_l,{\hat{v}}_k \rangle \langle {\hat{v}}_k,\gamma \rangle \\&\quad =\int ^{1}_{0}\int ^{1}_{0}{\hat{C}}_X(t,s)\gamma (t)\gamma (s)dtds+o_p(1), \end{aligned}$$

where the last equality follows from

$$\begin{aligned}&\frac{1}{n}\sum _{l=1}^n\langle X_l,\gamma \rangle \sum _{k=m+1}^n\langle X_l,{\hat{v}}_k \rangle \langle {\hat{v}}_k,\gamma \rangle =\sum _{k=m+1}^n\langle \gamma , {\hat{C}}_X{\hat{v}}_k\rangle \langle {\hat{v}}_k,\gamma \rangle \\&\quad =\sum _{k=m+1}^n{{\hat{\lambda }}_k}\langle {\hat{v}}_k,\gamma \rangle ^2\le {{\hat{\lambda }}_m}\sum _{k=m+1}^n\langle {\hat{v}}_k,\gamma \rangle ^2 \le O_p({{\hat{\lambda }}_m})=O_p\left( {\lambda }_m+\frac{m}{\sqrt{n}}\right) \\&\quad =O_p(n^{-{\frac{a}{a+2b}}}+n^{-{\frac{a+2b-2}{2a+4b}}})=o_p(1). \end{aligned}$$

Then, we have

$$\begin{aligned} \frac{1}{n}{\varvec{V}}^T({\varvec{I}}-{\varvec{S}}_m){\varvec{V}}={\varvec{V}}^T{\varvec{V}}-{\varvec{V}}^T{\varvec{S}}_m {\varvec{V}}=o_p(1). \end{aligned}$$

(15)

Applying Lemma 1 and $\varvec{\varepsilon }$ is independent of ${\varvec{Z}}$ and X, we have

$$\begin{aligned}&{\text{ E }}\left[ \frac{1}{n}({\varvec{Z}}\varvec{\beta })^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }\right] =0,\\&{\text {Var}}\left[ \frac{1}{n}({\varvec{Z}}\varvec{\beta })^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }\right] \nonumber \\&\quad =\frac{1}{n^2}{\text{ E }}\{({\varvec{Z}}\varvec{\beta })^T\varvec{\varepsilon }\varvec{\varepsilon }^T ({\varvec{I}}-{\varvec{S}}_m)({\varvec{Z}}\varvec{\beta })\}\\&\quad =\frac{1}{n^2}{\text{ E }}\{\text {tr}[\varvec{\varepsilon }\varvec{\varepsilon }^T ({\varvec{I}}-{\varvec{S}}_m)({\varvec{Z}}\varvec{\beta })({\varvec{Z}}\varvec{\beta })^T\}\\&\quad =\frac{\sigma ^2}{n^2}{\text{ E }}\{\text {tr}[({\varvec{Z}}\varvec{\beta })^T({\varvec{I}}-{\varvec{S}}_m)({\varvec{Z}}\varvec{\beta })]\}\\&\quad =\frac{\sigma ^2}{n^2}{\text{ E }}\{({\varvec{Z}}\varvec{\beta })^T({\varvec{I}}-{\varvec{S}}_m)({\varvec{Z}}\varvec{\beta })\} \\&\quad =o(1). \end{aligned}$$

Thus

$$\begin{aligned} \frac{1}{n}({\varvec{Z}}\varvec{\beta })^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }=o_p(1). \end{aligned}$$

(16)

Using the Cauchy-Schwarz inequality, (13) and (15), one can establish that

$$\begin{aligned} \frac{1}{n}({\varvec{Z}}\varvec{\beta })^T({\varvec{I}}-{\varvec{S}}_m)V=o_p(1). \end{aligned}$$

(17)

Similarly, using the Cauchy-Schwarz inequality, (14) and (15), one has

$$\begin{aligned} \frac{1}{n}{\varvec{V}}^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }=o_p(1). \end{aligned}$$

(18)

Then from (13)–(18) we get

$$\begin{aligned} \frac{1}{n}{\text{ RSS }}(H_0)=\varvec{\beta }^T{\varvec{B}}\varvec{\beta }+\sigma ^2+o_p(1). \end{aligned}$$

As a result

$$\begin{aligned} T_n=n\frac{\varvec{\beta }^T{\varvec{B}}\varvec{\beta }++o_p(1)}{\varvec{\beta }^T{\varvec{B}}\varvec{\beta }+\sigma ^2+o_p(1)}. \end{aligned}$$

Theorem 2 is proven by the positive definiteness of the matrix ${\varvec{B}}$. $\square$

Proof of Theorem 3

According to Theorem 3.1 in Shin (2009) and the model under ${{\widetilde{H}}}_A$

$$\begin{aligned} {Y}={\varvec{z}}^T\frac{{\varvec{C}}}{\sqrt{n}}+\int ^{1}_{0}\gamma (t)X(t)dt+\epsilon , \end{aligned}$$

one has

$$\begin{aligned} {\hat{\beta }}_1=\frac{W+{\varvec{C}}}{\sqrt{n}}+o_p\left( \frac{1}{\sqrt{n}}\right) , \end{aligned}$$

where W is a p-dimensional normally distributed vector with mean zero and covariance matrix $\sigma ^2{\varvec{B}}^{-1}$.

$$\begin{aligned}&\frac{1}{n}\big \{{\text{ RSS }}({{\widetilde{H}}}_0)-{\text{ RSS }}({{\widetilde{H}}}_A)\big \}\nonumber \\&\quad =\hat{\varvec{\beta }}_1^T\hat{{\varvec{B}}}\hat{\varvec{\beta }}_1\nonumber \\&\quad =\left\{ \frac{W+{\varvec{C}}}{\sqrt{n}}+o_p\left( \frac{1}{\sqrt{n}}\right) \right\} ^T\big ({\varvec{B}}+o_p(1)\big )\left\{ \frac{W+{\varvec{C}}}{\sqrt{n}}+o_p\left( \frac{1}{\sqrt{n}}\right) \right\} \nonumber \\&\quad =\frac{(W+{\varvec{C}})^T{\varvec{B}}(W+{\varvec{C}})}{n}+o_p\left( \frac{1}{n}\right) . \end{aligned}$$

(19)

Furthermore, similar to $\frac{1}{n}{\text{ RSS }}( H_0)$, one has

$$\begin{aligned}&\frac{1}{n}{\text{ RSS }}({{\widetilde{H}}}_0)\nonumber \\&\quad =\frac{1}{n}{\varvec{Y}}^T({\varvec{I}}-{\varvec{S}}_m){\varvec{Y}}\nonumber \\&\quad =\frac{1}{n}\left( \frac{{\varvec{ZC}}}{\sqrt{n}}+{\varvec{V}}+\varepsilon \right) ^T({\varvec{I}}-{\varvec{S}}_m)\left( \frac{{\varvec{ZC}}}{\sqrt{n}}+{\varvec{V}}+\varepsilon \right) \nonumber \\&\quad =\frac{1}{n^2}({\varvec{Z}}{\varvec{C}})^T({\varvec{I}}-{\varvec{S}}_m)({\varvec{Z}}{\varvec{C}})+\frac{1}{n}{\varvec{V}}^T ({\varvec{I}}-{\varvec{S}}_m){\varvec{V}}+\frac{1}{n}\varvec{\varepsilon }^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }\nonumber \\&\qquad +\frac{2}{n^{3/2}}({\varvec{Z}}{\varvec{C}})^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }+\frac{2}{n^{3/2}}({\varvec{Z}}{\varvec{C}})^T({\varvec{I}}-{\varvec{S}}_m){\varvec{V}} +\frac{2}{n}{\varvec{V}}^T({\varvec{I}}-{\varvec{S}}_m)\varvec{\varepsilon }\nonumber \\&\quad =\frac{1}{n}{\varvec{C}}^T{\varvec{B}}{\varvec{C}}+\sigma ^2+o_p(1)\nonumber \\&\qquad =\sigma ^2+o_p(1). \end{aligned}$$

(20)

The combination of (19) and (20) and the definition of non-central chi-squared distribution allow us to finish the proof of Theorem 3. $\square$