Abstract
We prove the generic equivalence between quasi-perfect equilibrium and sequential equilibrium. Combining this result with Blume and Zame (Econometrica 62:783–794, 1994) shows that perfect, quasi-perfect and sequential equilibrium coincide in generic games.

Similar content being viewed by others
Notes
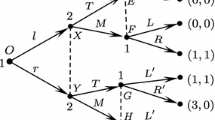
Note, however, that this generic result depends on the extensive form. E.g., in Fig. 1, after coalescing Player I’s two information sets, (l, B) becomes the unique (quasi-)perfect and sequential equilibrium. In particular, a generic extensive form game may become non-generic, or the other way around, after a finite sequence of inessential transformations (see Thompson 1952; or Elmes and Reny 1994).
In fact, by letting \(W^{\circ }\) denote the graph of the \(\varepsilon \)-perfect equilibrium correspondence we also provide an alternative proof to the generic equivalence between sequential and perfect equilibrium.
References
Aliprantis C, Border K (2006) Infinite dimensional analysis: a hitchhiker’s guide. Springer, Berlin
Blume L, Zame W (1994) The algebraic geometry of perfect and sequential equilibrium. Econometrica 62(4):783–794
Bochnak J, Coste M, Roy M (1998) Real algebraic geometry. Springer, Berlin
Elmes S, Reny J (1994) On the strategic equivalence of extensive form games. J Econ Theory 62(1):1–23
Govindan S, Wilson R (2006) Sufficient conditions for stable equilibria. Theor Econ 1(2):167–206
Govindan S, Wilson R (2012) Axiomatic equilibrium selection for generic two-player games. Econometrica 80(4):1639–1699
Hillas J, Kao T, Schiff A (2002) A semi-algebraic proof of the generic equivalence of quasi-perfect and sequential equilibria. University of Auckland, Mimeo
Kreps D, Wilson R (1982) Sequential equilibria. Econometrica 50:863–894
Kuhn H (1953) Extensive games and the problem of information. In: Kuhn H, Tucker A (eds) Contributions to the theory of games, vol 2. Princeton University Press, Princeton, pp 193–216
Mertens J-F (1995) Two examples of strategic equilibrium. Games Econ Behav 8(2):378–388
Osborne MJ, Rubinstein A (1994) A course in game theory. MIT Press, Cambridge
Reny J (1992) Backward induction, normal form perfection and explicable equilibria. Econometrica 60(3):627–649
Seidenberg A (1954) A new decision method for elementary algebra. Ann Math 60(2):365–374
Selten R (1975) Re-examination of the perfectness concept for equilibrium points in extensive games. Int J Game Theory 4:24–55
Tarski A (1951) A decision method for elementary algebra and geometry, 2nd edn. University of California Press, Berkeley
Thompson FB (1952) Equivalence of games in extensive form. RAND research, Memorandum 759.
van Damme E (1984) A relation between perfect equilibria in extensive form games and proper equilibria in normal form games. Int J Game Theory 13(1):1–13
Acknowledgments
We thank Priscila Man, the associate editor and two anonymous reviewers for thoughtful comments that improved the presentation and content of the paper. Carlos thanks financial support from UNSW ASBRG 2010. Jianfei thanks financial support from Shandong University grants IFYT12071 and 2013HW006. The usual disclaimer applies.
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper is based on the third chapter of Jianfei’s PhD thesis at The University of New South Wales. We recently learned that Hillas et al. (2002) proved Theorem 1 using a different approach. We thank John Hillas for providing a copy of that manuscript.
Appendix
Appendix
In what follows, if \(c\in C(h)\) we denote \(Z(h,c)\) the set of final nodes that come after some node in \(\{(x,c):x\in h\}\). Recall that a system of beliefs \(\mu \) assigns, for every player \(n\in \mathcal N \) and every \(h\in H_n\) a probability distribution on \(h\).
Proof of Proposition 1
Let \(s\in SE (u)\). We construct a sequence \(\{(u^t,\varepsilon ^t,s^t)\}_{t=1}^{\infty }\subset W^{\circ }\) that converges to \((u,0,s)\). Since \(s\) is a sequential equilibrium strategy, there is a system of beliefs \(\mu \) and a sequence \(\{(\mu ^t,s^t)\}_{t=1}^{\infty }\) converging to \((\mu ,s)\) such that \(s^t\in S^{\!\circ }\) and \(\mu ^t\) is derived from \(s^t\) using Bayes rule for every \(t\). Moreover, \((\mu ,s)\) is sequentially rational, i.e., for every player \(n\) and information set \(h\in H_n\), the strategy \(s_n\) prescribes optimal behavior at \(h\) given the value of \(\mu \) at \(h\) and the other players’ future behavior as described by \(s_{-n}\). Fix an element \(t\) of the sequence \(\{(\mu ^t,s^t)\}_{t=1}^{\infty }\). Define \(\varepsilon ^t=\max _{n,h,c}\left\{ s_n^t(c\mid h):\right. \left. s_n(c\mid h)=0\right\} \). We now construct a payoff vector \(u^t\) such that \((u^t,\varepsilon ^t,s^t)\in W^{\circ }\).
Let \(H^*_n\subset H_n\) be the collection of last information sets of player \(n\). For each information set \(h\in H_n^*\) and for each choice \(c\in C(h)\) compute:
Obtain the payoff vector \(w^t\) from \(u\) as follows:
Let \(H^{\prime }_n\) be the collection of last information sets in \(H_n\setminus H^*_n\). For each \(h^{\prime }\in H^{\prime }_n\) and for each choice \(c^{\prime }\in C(h^{\prime })\) let:
Obtain the utility vector \(\tilde{w}^t\) from \({w}^t\) according to:
In particular, note that if \(h\in H_n\) follows \(c^{\prime }\) then \(x^t_n(h^{\prime },c^{\prime })\) is added to player \(n\)’s utility value at every node in \(Z(h)\). Hence, player \(n\)’s optimal set of continuation strategies at \(h\) is the same under \(\tilde{w}^t\) as it is under \({w}^t\). Continue with this procedure with the remaining of information sets in \(H_n\). Repeat it, in the same fashion, for every other player \(m\ne n\). Since the game is finite, we stop after a finite number of steps obtaining a payoff vector \(u^t\) such that, by construction, \((u^t,\varepsilon ^t,s^t)\in W^{\circ }\).
To see that \(\{u^t\}_{t=1}^{\infty }\) converges to \(u\) note that, if it did not, there would be a player \(n\), an information set \(h\in H_n\) and a choice \(c\in C(h)\) with \(s_n(c\mid h)>0\) such that \(\{x^t(c,h)\}_{t=1}^{\infty }\) does not converge to zero. Letting \(h\) be a last information set in \(H_n\) within those with such a property, for some \(c\in C(h)\), the (bounded) sequence \(\{x^t(c,h)\}_{t=1}^{\infty }\) (passing to a sub-sequence if necessary) converges to some strictly positive number. Continuity of the function \(v^h_n\) implies that \(c\) is not a sequentially rational choice at \(h\) in the original game \(\Gamma (u)\).
Conversely, let \(\{(u^t,\varepsilon ^t,s^t)\}_{t=1}^{\infty }\subset W^{\circ }\) converge to \((u,0,s)\). Letting \(\mu ^t\) be derived from \(s^t\) using Bayes rule, we see that the limit point \((\mu ,s)\) of \(\{(\mu ^t,s^t)\}^{\infty }_{t=1}\) is a consistent assessment. Sequential rationality of \((\mu ,s)\) in \(\Gamma (u)\) follows again from the continuity of \(v^h_n\). Hence, \(s\in SE (u)\).
Rights and permissions
About this article
Cite this article
Pimienta, C., Shen, J. On the equivalence between (quasi-)perfect and sequential equilibria. Int J Game Theory 43, 395–402 (2014). https://doi.org/10.1007/s00182-013-0384-8
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00182-013-0384-8
Keywords
- Backwards induction
- Perfect equilibrium
- Quasi-perfect equilibrium
- Sequential equilibrium
- Lower-hemicontinuity
- Upper-hemicontinuity