1 Introduction

The issue of systemic risk attracts a lot of attention from academics as well as from regulators in the aftermath of the financial crisis of 2007–2009. Systemic risk refers to banks and other economic agents with substantial importance to the financial system due to their size (too big to fail) or their centrality within the financial network (too interconnected to fail). A bankruptcy of a systemically important financial institution can lead to the malfunctioning of the financial system or central banks and governments might be under pressure to interfere by bailing out respective firm. Due to these negative externalities, it is a crucial task for central banks and supervising agencies to identify systemically relevant firms.

A conventional quantitative risk measure is value-at-risk (VaR), which measures maximum losses at a certain confidence level. The Basel II Accord introduced VaR as a preferred measure for market risk. However, VaR is not capturing systemic risk adequately, as it is not capable to analyse the interdependency among firms. Given the subprime mortgage crisis in 2008, the Basel Committee on Banking Supervision has revised its Accords to focus on strong governance and risk management. Basel III is thus set up to control the systemic risk of the whole financial system, and it enforces additional requirements for identifying systemic risk important banks and generates demands on evaluating the interdependency of risk among banks. Adrian and Brunnermeier (2016) came up with conditional value-at-risk (CoVaR), a systemic extension of VaR. However, their original approach is restricted to analyse systemic risk in a linear and bivariate context. Namely, they focus primarily on the risk contribution of an individual financial firm to the entire system, controlling for variables indicating general macroeconomic conditions.

This paper provides a new perspective for estimating CoVaR using neural networks. Nonlinearity is an important issue for the prediction performance of risk measures due to the complex dependency channels of financial institutions (Chao et al. (2015)). Neural networks have proved to be a suitable method for fitting nonlinear functions. Over the last years, neural networks have become state-of-the-art models for prediction. They have been applied extensively and successfully to various fields, including image classification (Simonyan and Zisserman 2014) as well as speech recognition problems (Graves et al. 2013). Gu et al. (2020) and Bianchi et al. (2020) apply neural networks and other machine learning methods to asset pricing with promising results. We take the off-shelf neural network methodology and apply it to quantify financial risk. Our findings show that the quantile neural network-based approach provides a unique angle compared to the linear model for calibrating the systemic risk due to its flexibility. In particular, we find better out-of-sample prediction with our fine-tuned nonlinear neural network relative to the baseline linear quantile model of Koenker and Bassett (1978, 1982).

We briefly summarize the steps of calibrating the systemic risk using a quantile neural network procedure. In the first step, we estimate the VaR for each global systemically important financial institution (G-SIB) from the USA by regressing their stock returns on a set of risk factors using linear quantile regression. Next, we estimate the CoVaRs of the same firms using neural network quantile regression. To characterize the interdependency among banks, we regress the return of one asset on the remaining returns, respectively, and aggregate the results into a systemic fit. By approximating the conditional quantile with a neural network, we aim for capturing possible nonlinear effects. To estimate risk spillover effects across banks, we calculate the marginal effects by taking the derivative of the fitted quantile with respect to the other banks’ stock returns, evaluated at their VaR. By doing so, we come up with a network of spillover effects represented by an adjacency matrix. This adjacency matrix is time-varying, i.e. we estimate a network for each window in our moving window estimation procedure. In the final step, we propose three systemic risk measures building on the previous results. As a first measure, we propose the Systemic Fragility Index, which identifies the most vulnerable banks in a given financial risk network. The second measure is the Systemic Hazard Index, which identifies the financial institutions which potentially pose the largest risk to the financial system. These two measures characterize the firm-specific aspects of systemic risk. Thus, we propose a third measure which estimates the total level of systemic risk, the Systemic Network Risk Index.

Our empirical findings confirm that systemic risk increased sharply during the height of the financial crisis in 2008. We also observe a high level of systemic risk at the end of 2011 due to the uncertainty surrounding the European debt crisis. By comparing our systemic risk measure to the existing approaches for network-based interconnectedness, we find that our method offers a novel perspective due to the focus on the lower tail of the return distribution and due to the allowance for nonlinear dependencies. An out-of-sample comparison shows the superiority of our approach over a baseline model based on linear quantile regression. This leads to the conclusion that nonlinear effects are crucial for the modelling of systemic risk. Finally, we identify systemically relevant financial institutions during the financial crisis using our SFI and SHI measures. An advantage of our approach is the ability to capture the asymmetries of systemic risk, by differentiating between firms that affect and firms that are affected by the financial system. We also discover a risk cluster of four banks, which corresponds to the list of banks that received the largest funding in the course of the bank bailout of 2008.

This paper is an addition to the existing literature on systemic risk. Hautsch et al. (2014) modified the estimation of CoVaR further to analyse systemic risk in a multiple equation set-up using the LASSO. Härdle et al. (2016) followed up this set-up, and extended it to a nonlinear regression setting. In the meanwhile, there are numerous other methods for calibrating systemic risk. Acharya et al. (2017) built an economic model of systemic risk and measured the systemic risk externality of a financial institution by the systemic expected shortfall. Brownlees and Engle (2017) developed a systemic risk measure capturing the capital shortage given its degree of leverage and marginal expected shortfall. Diebold and Yılmaz (2014) analysed the connectedness of financial firms in a network context using forecast variance decompositions in a vector autoregressive framework. Bianchi et al. (2019) proposed a Markov-switching graphical SUR model to model systematic and systemic risk.

There is a growing literature on econometric analysis using neutral networks. White (1988) started to investigate the usefulness of adopting a neural network for economic prediction. Unfortunately, the message is that even with simple neural networks the prediction performance is not ideal due to the overfitting issues. Kuan and White (1994) provided a further overview of neural networks with some basic concepts and theory. White (1992) provided the theoretical foundations of a nonparametric quantile neural network approach allowing for cases of dependent data. In terms of economic risk prediction, Taylor (2000) is concerned with predicting conditional volatility by adopting a quantile neural network approach. Xu et al. (2016) considered a quantile neural network procedure for evaluating VaR in the stock market. Cannon (2011) focused on the computational perspective of a quantile neural network.

The remainder of this paper is organized as follows. Section 2 provides a brief introduction to neural networks in general and neural network quantile regression in particular. Section 3 describes in detail the methodology of this paper. After establishing the research framework step by step, we present the results in Section 4. Section 5 discusses the results and concludes.

2 Neural network quantile regression

2.1 Neural network sieve estimation

Neural networks attract increasing attention due to their success in a variety of prediction problems. Often described as a black box, single hidden layer neural networks can be seen as a special case of the nonparametric sieve estimator, see Grenander (1981) and Chen (2007). With increasing sample size n the complexity of the estimator of \(h_{\theta }\) is required to increase appropriately fast. The structure of the neural network sieve is as follows, with \(t = 1,2,\cdots ,n\),

$$\begin{aligned} \begin{aligned} Y_{t}&=h_{\theta }(X_{t})+\varepsilon _t \\&=\sum _{m=1}^{M_{n}}w_{m}^{o}\psi \left( \sum _{k=1}^{K}w_{k,m}^{h}X_{k,t}+b_{m}^{h}\right) +b_{o}+\varepsilon _{t} \end{aligned}\end{aligned}$$
(1)

where \(Y_{t}\) is the dependent variable, \(X_{t}\) is a K-dimensional vector of independent variables and \(\varepsilon _{t}\) is an error term. The nonlinear activation function \(\psi (\cdot )\) is assumed to be fixed and known. Typical choices are sigmoid functions, e.g. \(\psi (z)=\tanh (z)\) or the ReLU (rectifier linear unit) function, \(\psi (z)=\max (z,0)\). There are two types of parameters, hidden layer parameters \(w_{k,m}^{h}\) and \(b_{m}^{h}\) and output layer parameters \(w_{m}^{o}\) and \(b^{o}\). The sieve parameter space \(\Theta _{n}\) expands with n. In particular, the number of basis functions (i.e. the number of hidden nodes) goes to infinity, \(M_{n}\rightarrow \infty \) as \(n\rightarrow \infty \). Single layer neural networks have proved to be universal function approximators, as shown by Cybenko (1989) for sigmoid activation functions and Hornik et al. (1989) for the general case of bounded, non-constant activation functions. Sonoda and Murata (2017) extend the universal approximation property to unbounded activation functions, which includes the popular ReLU function.

The large sample properties of neural networks have been studied extensively in the literature. Notably, Chen and White (1999) show consistency and asymptotic normality of the nonparametric neural network sieve estimator under certain regularity conditions. Given that the number of basis functions grows appropriately with increasing sample size, the root mean square convergence rate to an unknown (suitably smooth) true function is of order \(o_{p}(n^{-1/4})\). This rate is crucial to obtain root-n asymptotic normality for plug-in estimators (Chen and Shen (1998)).

All of the above results concern with neural networks with a single hidden layer. The approximation theory and the asymptotic results of deep neural networks, i.e. neural networks with more than one hidden layer, are less understood compared to the shallow neural network case. Johnson (2018) shows that deep neural networks with limited width are not universal function approximators. Rolnick and Tegmark (2017) prove that deep neural networks can learn polynomial functions more efficiently (in terms of number of nodes required) than shallow ones.

2.2 Neural network sieves and quantile regression

Predominantly, neural networks have been applied to classification and mean regression problems. However, an extension to a quantile regression setting is straightforward. Consider the linear quantile regression equation for a fixed quantile level \(\tau \), as formulated in Koenker and Bassett (1978, 1982).

$$\begin{aligned} Y_{t}=X_{t}\beta +\varepsilon _{t},\quad t=1,\ldots ,n \end{aligned}$$
(2)

with \(Q^{\tau }(\varepsilon _{t}|X_{t})=0\). In this setting the dependent variable \(Y_{t}\) is modelled as a linear function of independent variables \(X_{t}\). The linear quantile estimator is then the solution to the following minimization problem:

$$\begin{aligned} \min _{\beta }\sum _{t=1}^{n}\rho _{\tau }\left( Y_{t}-X_{t}\beta \right) \end{aligned}$$
(3)

where \(\rho _{\tau }(z)=|z|\cdot |\tau -\mathbf{I} (z<0)|\) is the quantile loss function. This minimization problem can be formulated as a linear program and can thus be solved by simplex or interior point algorithms. Neural network quantile regression is a nonlinear generalization of this regression framework. Instead of using a linear function, the conditional quantile is approximated by a neural network sieve estimator as defined in 2.1. The resulting optimization problem is nonconvex and cannot be solved by linear programming methods:

$$\begin{aligned} \min _{\theta }\sum _{t=1}^{n}\rho _{\tau }\left\{ Y_{t}-h_{\theta }(X_{t})\right\} . \end{aligned}$$
(4)

A possible alternative is to use the gradient-based backpropagation algorithm of Rumelhart et al. (1988). The asymptotic properties of nonparametric neural network estimators for the conditional quantile are analysed in White (1992). Under certain regularity conditions the estimator is consistent, see Appendix A. This result holds both for i.i.d. and dependent data.

2.3 Regularization methods

Neural networks are prone to overfitting due to their high capacity. An effective tool to counteract overfitting lies in the choice of the structure and the hyperparameters of the neural network. In our single hidden layer setting, the most important hyperparameter is the number of hidden nodes, \(M_{n}\). Other relevant parameters are the number of epochs and the specification of the learning algorithm. Typically, hyperparameters are selected according to a cross-validation criterion. A different approach is to put an extra penalty term on the weight parameters, \(w_{k,m}^{h}\) and \(w_{m}^{o}\). We are considering both \(L_{1}\) and \(L_{2}\) penalties which we summarize under the term elastic net (Zou and Hastie (2005)). This penalization method leads to the following optimization problem:

$$\begin{aligned} \min _{h_{\theta }}\sum _{t=1}^{n}\rho _{\tau }\left\{ Y_{t}-h_{\theta }(X_{t})\right\} +\lambda _{1}\Vert (w_{k,m}^{h\top },w_{m}^{o\top })^{\top }\Vert _{1}+\lambda _{2}\Vert (w_{k,m}^{h\top },w_{m}^{o\top })^{\top }\Vert _{2}^{2} \end{aligned}$$
(5)

where \(\Vert \cdot \Vert _{1}\) is the \(L_1\)-norm, \(\Vert \cdot \Vert _{2}\) is the \(L_{2}\)-norm. \(\lambda _{1}\) and \(\lambda _{2}\) are regularization parameters. A different method to prevent overfitting is the dropout method, proposed by Hinton et al. (2012) and Srivastava et al. (2014). In each iteration of the backpropagation algorithm, a given node is only considered with a probability \(1-p\). Consequently, each node is excluded with a probability p which is defined as the dropout rate. The motivation for this is to counteract memorization of the data by preventing co-adaptation of the nodes. Dropout is referred to be an ensemble method, as the final model is a result of training multiple models with reduced capacity.

3 Methodology to calibrate systemic risk

In this section, we explain the details of our systemic risk analysis. Our methodology involves four steps. The first step is concerned with the estimation of VaR based on a linear quantile regression using a set of risk factors as explanatory variables. The results are used in the next step to estimate the CoVaR for each financial institution using a quantile regression neural network. Next, we calculate marginal effects to model systemic risk spillover effects, resulting in a time-varying systemic risk network. In the final step, we propose three systemic risk measures based on this systemic risk network.

3.1 Step 1: estimation of VaR

VaR is defined as the maximum loss over a fixed time horizon at a certain level of confidence. The Basel II Accord introduced VaR as the preferred measure for market risk. The calculation of VaR functions as the basis for capital requirements of financial institutions. Mathematically, it is the \(\tau \)-quantile of the return distribution:

$$\begin{aligned} {\text {P}}(X_{i,t}\le {\text {VaR}}_{i,t}^{\tau })=\tau , \end{aligned}$$
(6)

where \(X_{i,t}\) is the return of a financial firm i at time t and \(\tau \in (0,1)\) is the quantile level. There exist numerous ways to estimate VaR. We refer to Kuester et al. (2006) for an extensive overview. One example is to assume a parametric model, and the most popular formulation involves the estimation of the latent volatility process via the GARCH model. Other approaches are based on the direct estimation of the conditional quantiles. Chernozhukov and Umantsev (2001) combine linear quantile regression with extreme value theory (EVT) to estimate VaR for extreme quantile levels. Chao et al. (2015) and Härdle et al. (2016) estimate VaR by using linear quantile regression on a set of macro-state variables.

In this study, we compare three different specifications. First, we consider the dynamic quantile approach of Engle and Manganelli (2004), which is called CAViaR. The VaR is modelled as a latent process. We consider the symmetric absolute value (SAV) specification,

$$\begin{aligned} {\text {VaR}}_{i,t}^{SAV,\tau }=\beta _{i,1}+\beta _{i,2}{\text {VaR}}_{i,t-1}^{SAV,\tau }+\beta _{i,3}|X_{i,t-1}|. \end{aligned}$$
(7)

Here, the current level of VaR is determined by its lagged value as well as by the absolute value of the lagged return. Second, we consider the asymmetric slope (AS) CAViaR specification,

$$\begin{aligned} {\text {VaR}}_{i,t}^{AS,\tau }=\beta _{i,1}+\beta _{i,2}{\text {VaR}}_{i,t-1}^{AS,\tau }+\beta _{i,3}(X_{i,t-1})^{+}+\beta _{i,4}(X_{i,t-1})^{-}. \end{aligned}$$
(8)

This specification allows for different responses to negative and positive returns. Finally, we consider the approach of Härdle et al. (2016). The VaR of each firm i is estimated by linear quantile regression using a set of macro-state variables \(M_{t-1}\).

$$\begin{aligned} X_{i,t}=\alpha _{i}+\gamma _{i}M_{t-1}+\varepsilon _{i,t}, \end{aligned}$$
(9)

where the conditional quantile of the error term \(Q^{\tau }(\varepsilon _{i,t}|M_{t-1})=0\). The VaR estimate is the fitted value of the quantile regression,

$$\begin{aligned} {\text {VaR}}_{i,t}^{LQR,\tau }=\widehat{\alpha }_{i}+\widehat{\gamma }_{i}M_{t-1}. \end{aligned}$$
(10)

VaR is a frequently used measure for understanding the critical risk level for an individual financial institution. The drawback of VaR is that it cannot account for dependency in a systemic context. Estimating VaR as an individual risk measure is a necessary first step to prepare for calibrating conditional risk.

3.2 Step 2: Estimation of CoVaR with neural network quantile regression

CoVaR was introduced as a systemic extension of standard VaR by Adrian and Brunnermeier (2016). Similar to VaR, it is a risk measure defined as a conditional quantile of the return distribution. But deviating from the VaR concept, CoVaR is contingent on a specific financial distress scenario. The motivation for using CoVaR is the identification of systemically important banks. For the distress scenario, we assume that all other firms are at their VaR. By doing this, we follow the reasoning of Hautsch et al. (2014) and Härdle et al. (2016).

$$\begin{aligned} {\text {P}}(X_{j,t}\le {\text {CoVaR}}^{\tau }_{j,t}|X_{-j,t}={\text {VaR}}_{-j,t}^{\tau })=\tau , \end{aligned}$$
(11)

where \(X_{-j,t}\) is a vector of returns of all firms except j at time t and \({\text {VaR}}_{-j,t}^{\tau }\) is the corresponding vector of VaRs.

CoVaR can be estimated as a fitted conditional quantile, building on the results for the VaRs obtained in step 1. Chao et al. (2015) and Härdle et al. (2016) find evidence for nonlinearity in the dependence between pairs of financial institutions. Hence, linear quantile regression might not be an appropriate procedure to estimate the risk spillovers, as the interdependencies are potentially different in a state of worsening market conditions. The conditional quantile function of one bank on another may react nonlinearly to the change of critical level of another firm. We therefore propose the use of neural network quantile regression. The flexibility of the approach allows detecting possible nonlinear dependencies in the data.

The conditional quantile of bank j’s returns is regressed on the returns of all other banks and using a neural network as defined in Section 2.2:

$$\begin{aligned} \begin{aligned} X_{j,t}&=h_{\theta }(X_{-j,t})+\varepsilon _{j,t},\\&=\sum _{m=1}^{M_{n}}w_{m}^{o}\psi \left( \sum _{k\ne j}^{K}w_{k,m}^{h}X_{k,t}+b_{m}^{h}\right) +b^{o}+\varepsilon _{j,t}, \end{aligned} \end{aligned}$$
(12)

with the conditional quantile of error term \(Q^{\tau }(\varepsilon _{j,t}|X_{-j,t})=0\). To calculate the CoVaR of firm j, the fitted neural network has to be evaluated at the distress scenario:

$$\begin{aligned} {\text {CoVaR}}_{j,t}^{\tau }=\widehat{h}_{\theta }({\text {VaR}}_{-j,t}^{\tau }), \end{aligned}$$
(13)

where \(\widehat{h}_{\theta }\) is the estimated neural network. Nonlinearity is introduced by the use of the nonlinear activation function. CoVaR can be interpreted as the hypothetical \(\tau \)-quantile of the loss distribution if we are in a hypothetical distress scenario. In our case, this distress scenario is all other firms being at their VaR.

3.3 Step 3: calculation of risk spillover effects

Based on the weights estimated by the neural network quantile regression procedure, it is now possible to obtain risk spillover effects between each directed pair of banks. We propose to estimate the spillover effects by taking the partial derivative of the conditional quantile of firm j’s return with respect to the return of firm i.

$$\begin{aligned} \frac{\partial Q^{\tau }(X_{j,t}|X_{-j,t})}{\partial X_{i,t}}&=\frac{\partial }{\partial X_{i,t}} \sum _{m=1}^{M_{n}}w_{m}^{o}\ \psi \left( \sum _{k\ne j}^{K}w_{k,m}^{h}X_{k,t}+b_{m}^{h}\right) +b^{o}. \end{aligned}$$
(14)

In the case of a sigmoid tangent activation function, we have

$$\begin{aligned} \frac{\partial Q^{\tau }(X_{j,t}|X_{-j,t})}{\partial X_{i,t}}=\sum _{m=1}^{M_{n}}w_{m}^{o}w_{i,m}^{h}\psi ^{\prime }\left( \sum _{k\ne j}^{K}w_{k,m}^{h}X_{k,t}+b_{m}^{h}\right) \end{aligned}$$
(15)

with

$$\begin{aligned} \psi ^{\prime }(z)&=\frac{2}{(\exp ^{-z/2}+\exp ^{z/2})^{2}}. \end{aligned}$$
(16)

In the case of a ReLu activation function, we have

$$\begin{aligned} \frac{\partial Q^{\tau }(X_{j,t}|X_{-j,t})}{\partial X_{i,t}}=\sum _{m=1}^{M_{n}}w_{m}^{o}w_{i,m}^{h}{} \mathbf{I} \left( \sum _{k\ne j}^{K}w_{k,m}^{h}X_{k,t}+b_{m}^{h}>0\right) , \end{aligned}$$
(17)

where \(\mathbf{I} (\cdot )\) is the indicator function. Note that the non-differentiability of the ReLU function is not an issue in practice since the input of the function is zero with probability zero. As we are interested in the lower tail dependence, we consider the marginal effect evaluated at the distress scenario as defined in the previous subsection:

$$\begin{aligned} \left. \frac{\partial Q^{\tau }(X_{j,t}|X_{-j,t})}{\partial X_{i,t}}\right| _{X_{-j,t}={\text {VaR}}_{-j,t}^{\tau }} =\sum _{m=1}^{M_{n}}w_{m}^{o}w_{i,m}^{h}\ \psi ^{\prime }\left( \sum _{k\ne j}^{K}w_{k,m}^{h}{\text {VaR}}_{k,t}^{\tau }+b_{m}^{h}\right) . \end{aligned}$$
(18)

Calculating such a marginal effect for each directed pair of firms yields an off-diagonal adjacency matrix of risk spillover effects at time t:

$$\begin{aligned} A_{t}=\begin{pmatrix} 0 &{} a_{12,t} &{} \ldots &{} a_{1K,t} \\ a_{21,t} &{} 0 &{} \ldots &{} a_{2K,t} \\ \vdots &{} \ldots &{} \ddots &{} \vdots \\ a_{K1,t} &{} a_{K2,t} &{} \ldots &{} 0 \end{pmatrix}, \end{aligned}$$
(19)

with elements defined as absolute values of marginal effects:

$$\begin{aligned} a_{ji,t}= {\left\{ \begin{array}{ll} \left| \left. \frac{\partial Q^{\tau }(X_{j,t}|X_{-j,t})}{\partial X_{i,t}}\right| _{X_{-j,t}={\text {VaR}}_{-j,t}^{\tau }} \right| , &{} \text {if }j\ne i \\ 0, &{} \text {if }j=i \end{array}\right. }. \end{aligned}$$
(20)

Note that the risk spillover effects are not symmetric in general, thus \(a_{ji,t}\ne a_{ij,t}\). This adjacency matrix specifies a weighted directed graph modelling the systemic risk in the financial system.

3.4 Step 4: Network analysis of spillover effects

To further analyse the systemic relevance of the financial institutions, we can calculate several network measures building on the work of Diebold and Yılmaz (2014). They measure the connectedness of financial firms in terms of variance decomposition in a vector autoregressive framework. Their methodology is thus limited to capturing linear spillover effects.

First, the total directional connectedness to firm j at time t is defined as the sum of absolute marginal effects of all other firms on j.

$$\begin{aligned} C_{j\leftarrow \cdot ,t}=\sum _{i=1}^{K}a_{ji,t}. \end{aligned}$$
(21)

Analogously, one can define the total directional connectedness from firm i at time t as the sum of absolute marginal effects from i to all other firms.

$$\begin{aligned} C_{\cdot \leftarrow i,t}=\sum _{j=1}^{K}a_{ji,t}. \end{aligned}$$
(22)

Lastly, Diebold and Yılmaz (2014) define the total connectedness at time t as the sum of all absolute marginal effects.

$$\begin{aligned} C_{t}=\frac{1}{K}\sum _{i=1}^{K}\sum _{j=1}^{K}a_{ji,t}. \end{aligned}$$
(23)

The total connectedness is a measure for the connectedness level of the entire system without differentiating the roles of individual nodes of the network. Building on this network analysis, we refine the approach by incorporating VaR and CoVaR in the measurement of the systemic risk relevance. In particular, we propose the Systemic Fragility Index (SFI) and the Systemic Hazard Index (SHI) to rank financial institutions according to their relevance.

$$\begin{aligned} SFI_{j,t}&=\sum _{i=1}^{K}\left( 1+|{\text {VaR}}_{i,t}^{\tau }|\right) \cdot a_{ji,t}, \end{aligned}$$
(24)
$$\begin{aligned} SHI_{i,t}&=\sum _{j=1}^{K}\left( 1+|{\text {CoVaR}}_{j,t}^{\tau }|\right) \cdot a_{ji,t}. \end{aligned}$$
(25)

The SFI is a measure for the risk exposure of a financial institution j. It increases if those adjacency weights pointing to j are large and also if the VaRs of firms i (i.e. the risk factors for j) increase. This implies that the SFI will increase in times of financial distress. The index can be used by regulators to identify banks which have a high exposure to the tail risk in the financial system.

The SHI is a measure for the risk contribution of firm i to the whole system. It depends on the out-going adjacency weights from i weighted by the other firms’ CoVaRs. Thus, the SHI tends to be large if the other firms are already affected by whole system, weighted by their CoVaR. The SFI and the SHI are firm-specific. It should be noted that our approach allows to model asymmetries. For instance, a firm which has a high tail risk exposure does not need to have a large impact on the whole system and vice versa. In contrast to the original CoVaR approach of Adrian and Brunnermeier (2016), our approach of identifying systemically important financial institutions has two advantages. First, we are able to capture possible nonlinear relationships in the data. Second, our approach operates in a network context which goes beyond the pairwise analysis proposed in the original CoVaR methodology.

As a third measure, we propose the Systemic Network Risk Index (SNRI), a measure for the total systemic risk in the financial system which depends on the marginal effects, the outgoing VaRs, and the incoming CoVaRs. It is a measure for tail connectedness focusing a lower quantile level.

$$\begin{aligned} SNRI_{t}=\sum _{i=1}^{K}\sum _{j=1}^{K}(1+|{\text {VaR}}_{i,t}^{\tau }|)\cdot (1+|{\text {CoVaR}}_{j,t}^{\tau }|)\cdot a_{ji,t}. \end{aligned}$$
(26)

Lastly, we define the adjusted adjacency matrix,

$$\begin{aligned} \widetilde{A}_{t}=\begin{pmatrix} 0 &{} \widetilde{a}_{12,t} &{} \ldots &{} \widetilde{a}_{1K,t} \\ \widetilde{a}_{21,t} &{} 0 &{} \ldots &{} \widetilde{a}_{2K,t} \\ \vdots &{} \ldots &{} \ddots &{} \vdots \\ \widetilde{a}_{K1,t} &{} \widetilde{a}_{K2,t} &{} \ldots &{} 0 \end{pmatrix} \end{aligned}$$
(27)

with elements defined as:

$$\begin{aligned} \widetilde{a}_{ji,t}= {\left\{ \begin{array}{ll} a_{ji,t}\cdot (1+|{\text {VaR}}_{i,t}^{\tau }|)\cdot (1+|{\text {CoVaR}}_{j,t}^{\tau }|), &{} \text {if }j\ne i \\ 0, &{} \text {if }j=i \end{array}\right. }. \end{aligned}$$
(28)

The adjusted adjacency matrix accounts for the level of outgoing VaRs and incoming CoVaRs and is an improved representation of risk spillover effects. Systemic spillover effects are thus determined by the marginal effects of the neural network quantile regression procedure as well as by the VaRs and CoVaRs of the considered banks.

4 Empirical study: US G-SIBs

4.1 Data

For the empirical application of our systemic risk methodology, we are focusing on the global systemically important banks (G-SIBs) from the USA selected by the Financial Stability Board (FSB), see Table 1. These eight banks constitute systemic risk relevance to the global financial system and are deemed to be too-big-to-fail. We consider daily log returns in a time period between 4 January 2007 and 31 May 2018. The data is obtained from Yahoo Finance.

Table 1 List of G-SIBs in the USA
Full size table

In addition to these stock return data, we consider daily observations of the following set of macro-state variables:

  1. i)

    Implied Volatility Index (VIX), from Yahoo Finance;

  2. ii)

    the weekly S&P500 index returns, from Yahoo Finance;

  3. iii)

    Moody’s Seasoned Baa Corporate Bond Yield Relative to Yield on 10-Year Treasury Constant Maturity from Federal Reserve Bank of St. Louis;

  4. iv)

    10-Year Treasury Constant Maturity Minus 3-Month Treasury Constant Maturity from Federal Reserve Bank of St. Louis.

These macro-variables are the common risk factors for the estimation of VaR in the first step of our systemic risk methodology.

4.2 Model selection and out-of-sample performance

The estimation of CoVaR based on neural network quantile regression involves several tuning parameters. Most importantly, we have to make a choice about the activation function and determine the sizes and structure of the neural network. We recalibrate these tuning parameters at the start of each year in a data-driven way. We propose the following moving-window model selection and evaluation procedure.

Following the common approach in the literature, e.g. Gu et al. (2020), Bianchi et al. (2020), we repeatedly divide our sample into three disjoint subsamples. These subsamples are consequential to maintain the time series structure of the data. The first sample is called the training set, which is denoted by \(\mathcal {T}_{1}\). The training set is used to estimate the weight and bias parameters of the neural network for each candidate model specification. The performance is then evaluated using the validation set, denoted by \(\mathcal {T}_{2}\). The tuning parameters are optimized by choosing the model specification which minimizes the objective function. This division into training and validation sets is an effective way to counteract overfitting. However, the validation fit is not truly out-of-sample since it is used to select the tuning parameters. Therefore, we finally consider the last subsample as the test set, which is denoted by \(\mathcal {T}_{3}\). The test set is used to get an unbiased estimate of the method’s performance.

To evaluate the predictive performance of our method, we calculate the out-of-sample average quantile loss, (\(AQL^{oos}\)),

$$\begin{aligned} AQL^{oos}=\frac{1}{|\mathcal {T}_{3}|}\sum _{t\in \mathcal {T}_{3}}\rho _{\tau }\left\{ X_{j,t}-\widehat{Q}^{\tau }\left( X_{j,t}|X_{-j,t}\right) \right\} . \end{aligned}$$
(29)

The tuning parameters include: the number of nodes in the neural network, the \(L_{1}\) and \(L_{2}\) penalty terms on the weight parameters and the dropout probability p. We recalibrate the tuning parameters for each financial firm at the start of the year. We choose a sample size of 200 and 50 days for the training and validation data sets, respectively. This corresponds to 1 year of daily data. We evaluate the performance on the subsequent 250 days in the test set. By recalibrating the tuning parameters annually, we end up with ten windows in total. A visualization of the sample splitting scheme can be found in Fig. 1. In the following, we summarize the steps of our model selection and the evaluation procedure.

  1. Step 1:

    Split the data into training (\(\mathcal {T}_{1}\)), validation (\(\mathcal {T}_{2}\)) and test set (\(\mathcal {T}_{3}\)) for each window.

  2. Step 2:

    For each bank j and each window, fit the conditional quantile of \(X_j\) contingent on \(X_{-j}\) using \(\mathcal {T}_{1}\).

  3. Step 3:

    Choose the model specification which minimizes the average quantile loss based on \(\mathcal {T}_{2}\) .

  4. Step 4:

    Calculate \(AQL^{oos}\) based on the tuned neural network using \(\mathcal {T}_{3}\).

Fig. 1
figure 1

Visualization of the rolling window model selection scheme. Training data (blue), validation data (orange) and test data (red)

Full size image

Finally, we compare the predictive performance of our neural network quantile regression procedure to a simple baseline model based on the linear quantile regression,

$$\begin{aligned} X_{j,t}=\beta _{0}+\sum _{i\ne j}^{K}X_{i,t}\beta _{i}+\varepsilon _{j,t}, \end{aligned}$$
(30)

with \(Q^{\tau }(\varepsilon _{t}|X_{-j,t})=0\). The baseline model is estimated on training and validation data sets \(\mathcal {T}_{1}\) and \(\mathcal {T}_{2}\). The estimation does not involve any tuning parameters so we can make use of the combined data set. The out-of-sample forecast performance is then evaluated using the holdout data \(\mathcal {T}_{3}\). We apply the test of Diebold and Mariano (2002) to compare the forecast performance. The test statistic is based on the quantile loss differentials between the neural network and the linear baseline model and has an asymptotic standard normal distribution. We choose a significance level of \(1\%\). The test results are reported in Table 2.

For all of the financial institutions in our sample, the neural network fit performs better than the linear quantile regression fit. The outperformance of the neural network forecast is statistically significant for the majority of banks (seven out of eight). Only for Goldman Sachs the Diebold–Mariano fails to reject the null hypothesis of similar forecast performance. Overall, the use of a more complex model like a neural network appears to be recommendable. A plausible explanation for this is that a linear model is not capable to capture the complex interdependencies of financial firms under distress.

Table 2 Results of the Diebold–Mariano test comparing the neural network to the linear baseline model
Full size table

For the selection of the VaR approach used in the first step of our systemic risk analysis, we compare the predictive performance of the three candidate models introduced in Section 3. We consider a sliding window of 250 days, which is used for estimation to predict the next day’s conditional \(5\%\) quantile of the returns. The results are displayed in Table 3. For every bank in our sample, the linear quantile approach performs best. Results from the Diebold–Mariano test show that the difference is significant at the \(1\%\) confidence level after accounting for the multiple testing issue by using the Bonferroni correction for critical values. In the following, all VaR calculations are based on the linear quantile approach.

Table 3 Out-of-sample average quantile loss of the candidate models for every financial institution (\(\times 10^3\))
Full size table

4.3 Estimation results

4.3.1 VaR and CoVaR

Fig. 2
figure 2

Plot of Returns (black dots), VaR (blue line) and CoVaR estimated by neural network quantile regression (red line) for Wells Fargo

Full size image
Fig. 3
figure 3

Fitted quantile regression neural network for Wells Fargo on 13 March 2008. Red connections indicate negative weights, blue connections indicate positive weights

Full size image

As explained in Section 3, the analysis is carried out in four steps. In the first two steps, VaR and CoVaR are estimated for each firm, using linear quantile regression and neural network quantile regression, respectively. To account for potential non-stationarity, we employ a sliding window estimation framework for both measures. The window size is chosen to be 250 observations (representing 1 year of daily stock returns). We choose a quantile level of \(\tau =5\%\), which is the standard in the related literature, see Hautsch et al. (2014) and Härdle et al. (2016). A lower value for the quantile level leads to less reliable estimates, due to the inverse relation of the variance and the density of the error term. As a sensitivity analysis, we also report the results for \(\tau =1\%\), see Figs. 11 and 12 in Appendix B. The results are robust with respect to the choice of the quantile level.

The estimation results for Wells Fargo are visualized in Fig. 2. The estimated VaR and CoVaR follow a similar pattern. In the course of the financial crisis both risk measures explode, indicating an increase in systemic risk during this period. A second persistent spike appears in the second half of 2011 caused by the European debt crisis. In the following, both VaR and CoVaR stabilize with a few non-persistent spikes. Similar patterns can be found in the estimation results for the other financial institutions (see Fig. 13 in Appendix B). An example of a fitted neural network is visualized in Fig. 3.

4.3.2 Risk spillover network

Fig. 4
figure 4

Time average of risk spillover effects across banks for different time periods

Full size image
Fig. 5
figure 5

Time average of risk spillover effects across banks after thresholding (\(\widetilde{a}_{ji}>0.4\)) for different time periods

Full size image

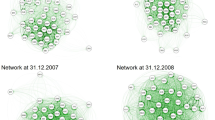
Based on the estimation results of the neural network quantile regression procedure and on the fitted VaRs and CoVaRs, we calculate the directional spillover effects for each pair of banks over our prediction horizon. The result is a time-varying weighted adjusted adjacency matrix (as defined in Equation 27). This risk spillover network provides insights into the cross section and the time dynamics of systemic risk. Figure 4 visualizes the evolution of the network in the course of the financial crisis. The first half of 2008 shows a moderate level of lower tail connectedness. This setting changes dramatically in the second half of 2008 with the bankruptcy of Lehman Brothers. As a consequence, the United States Department of the Treasury was compelled to bail out financial institutions to avoid a total collapse of the financial system. Also, the Federal Reserve Bank had to adjust its monetary policy. The time average of the adjacency matrix for 2009 shows a continuing state of financial distress. However, compared to the previous periods one can visually identify a risk cluster in the lower left part of the adjacency matrix. Finally, 2010 shows a decline in systemic risk spillover effects caused by a regained trust in the financial system. Figure 5 restricts the visualization to the largest edges of the financial risk network. As a first observation, spillover effects across banks tend to be symmetric. If bank i has a large impact on bank j, the converse is also very likely. A second observation is the identification of the risk cluster mentioned above. This cluster includes four financial institutions, Citigroup, Bank of America, JP Morgan and Wells Fargo. This cluster coincides with the list of the largest beneficiaries of the bailout program in 2008 and 2009.

4.3.3 Network risk measures

Fig. 6
figure 6

Time series of the SNRI

Full size image
Fig. 7
figure 7

Plot of SNRI (black line), the Granger causality measure of Billio et al. (2012) (red line) and total connectedness of Diebold and Yılmaz (2014) (blue line). Dashed vertical line marks the bailout and acquisition of Bear Stearns by JP Morgan on 14 March 2008, the dotted vertical line indicates the bankruptcy of Lehman Brothers on 15 September 2008

Full size image

In this subsection, we estimate the systemic risk measures using the results from the previous steps. First, we consider the Systemic Network Risk Index (SNRI), as a measure for total systemic risk in the financial system. Figure 6 shows the development over time. As expected, we see a sharp increase in systemic risk during the financial crisis in the second half of 2008. A second peak appears in the second half of 2011 as a result of the uncertainties associated with the European debt crisis. After a short period of stabilization, we see another rise in systemic risk from 2014 till 2016. In contrast to the previous peaks, this increase appears to be more gradual.

We now discuss the systemic risk measure calibration during the financial crisis in detail. We restrict our focus on the 2-year period, i.e. from the start of 2008 to the end of 2009. We compare our SNRI to the Granger causality measure of Billio et al. (2012) and the total connectedness measure based on variance decomposition proposed by Diebold and Yılmaz (2014). Both measures are estimated using the same set of financial institutions and a rolling window of 250 days. The results are displayed in Fig. 7. As reference dates, we have added the bailout of Bear Stearns and the resulting acquisition by JP Morgan on 14 March 2008, as well as the bankruptcy of Lehman Brothers on 15 September 2008. A few significant differences in the time series of the risk measures are apparent. While the Granger causality measure and the total connectedness increase sharply after the Bear Stearns event, the SNRI decreases slightly. In contrast to both alternatives, our measure is exclusively concerned with the lower quantile of the return distribution. We infer that the resulting intervention had a calming effect on the financial markets and thus prevented an increase in lower tail dependence. The Bear Stearns shock seemed to have a systematic but not necessarily a systemic effect. In contrast, we observe a simultaneous sharp increase in all three measures immediately after the Lehman Brothers bankruptcy. The increase in connectedness thus affected the mean as well as the lower tail of the distribution. We deduce that the shock from the Lehman bankruptcy had a truly systemic impact. In the aftermath of the collapse, the SNRI has its maximal point in March of 2009 and remains at a high level until the second half of the same year. The comparing measures have an earlier peak in the end of 2008 followed by a fast decrease. We conclude that the SNRI complements the network-based risk measures proposed by Billio et al. (2012) and Diebold and Yılmaz (2014) as it is more sensitive to shocks in the lower tail.

Fig. 8
figure 8

Co-movement of the SNRI (black line) and the aggregate SRISK (Brownlees and Engle (2017), red line)

Full size image

We also compare the SNRI to the aggregated SRISK of Brownlees and Engle (2017) in Fig. 8. One can identify a co-movement of both indices. In particular, both the financial crisis and the European debt crisis lead to a sharp increase in both risk measures. However, we have to acknowledge that the aggregated SRISK already detects vulnerabilities in the financial system as early as the beginning of 2008. The reason for this is that the SRISK incorporates additional information on micro-prudential variables, namely the book value of debt and the quasi value of assets. An advantage of the SNRI is that it is entirely based on market data. Also, the SRISK requires assumptions on a number of structural parameters, such as the prudential capital ratio and the threshold loss, while our approach does not. Finally, another advantage of our approach is the estimation of spillover effects in a network context.

Table 4 Ranking of financial institutions according to their SFI averaged over different time intervals
Full size table
Table 5 Ranking of financial institutions according to their SHI averaged over different time intervals
Full size table

While the SNRI is an index for total systemic risk, we now consider firm-specific measures. Table 4 ranks financial firms according to their Systemic Fragility Index (SFI). A large SFI indicates high systemic exposure to the financial system. Our findings suggest that Citigroup is among the most fragile banks during the height of the financial crisis, being top-ranked in the first and in the second half of 2008. Due to heavy exposure to troubled mortgages, the US government decided to bail out the bank in November 2008. In the periods following the bail-out, Citigroup’s SFI rank dropped sharply. Figure 9 shows the time dynamics of the SFI of Citigroup. Another high-ranked financial institution is Bank of America, which is on position three in the second half of 2008 and the number one in 2009. In contrast, State Street Corporation is ranked at the bottom of the table throughout 2008 and 2009. This result is plausible since State Street was the first major financial institution to pay back its loans to the US Treasury in July 2009.

We conduct a similar ranking with respect to the Systemic Hazard Index (SHI), which ranks the financial institutions according to the risk contributed to the financial system. In each of the time periods, we consider, JP Morgan is listed in the top two of the ranking. Similarly, Bank of America is ranked in the top four consistently, being the second highest ranked bank in the first half of 2008. Figure 10 visualizes the time dynamics of the SHI for Bank of America. In the aftermath of the crisis in 2009, Wells Fargo also emerges as a systemic risk factor to the financial system. An advantage of our approach is that we are able to differentiate between firms, which transmit systemic risk, and firms which are affected by systemic risk. By doing this, we capture the asymmetric nature of the systemic risk. As an example, JP Morgan is ranked high according to the SHI in 2008 but relatively low in SFI. The opposite can be observed for Citigroup, which is ranked low in SHI and high in SFI during the same time periods. However, State Street is at the bottom of both rankings during the height of the financial crisis, implying that it is neither a large risk factor nor strongly affected by the financial system.

Fig. 9
figure 9

Time series of the SFI for Citigroup

Full size image
Fig. 10
figure 10

Time series of the SHI for Bank of America

Full size image

5 Conclusion

This paper proposes a novel approach to estimate the conditional value-at-risk (CoVaR) of financial institutions based on neural network quantile regression. Our methodology allows for the identification of risk spillover effects across banks in a nonlinear and multivariate context. We define three network-based measures for systemic risk, the Systemic Fragility Index and the Systemic Hazard Index as firm-specific measures and the Systemic Network Risk Index as a measure for the overall risk in the financial system. These measures quantify the connectedness of the financial system while restricting the analysis on the lower tail of the distribution. The neural network framework allows us to model systemic risk in a highly nonlinear setting. A comparison to a linear baseline model shows the predictive superiority of our neural network approach in terms of the out-of-sample performance.

We apply our methodology to global systemically important banks (G-SIBs) from the USA in the period 2007–2018. Consistent with previous findings in the literature, we observe the Systemic Network Risk Index increasing sharply during the financial crisis and during the European debt crisis. A comparison to the connectedness measures proposed in Billio et al. (2012) and Diebold and Yılmaz (2014) shows that our systemic risk measure captures different aspects of connectedness and offers therefore a new perspective on systemic risk. Furthermore, our approach allows to identify a risk cluster of banks which corresponds to the list of banks that receive the largest amount of funding from the US Department of Treasury. By ranking the financial firms according to their Systemic Fragility Index and their Systemic Hazard Index, we are able to identify those firms which bear significant exposure to the financial system and those firms which impose the greatest risk to the financial system.