Abstract
This study investigates whether the September 11 terrorist attacks had any impacts on the labor market outcomes of refugees resettled in the United States, who should be distinguished from economic migrants or usual nonnatives. Furthermore, this paper sheds unprecedented light on whether those impacts were heterogeneous depending on a refugee’s ethnicity or religion. In terms of econometric methods, this research attempts to allow for the violation of the conventional condition of independently and identically distributed (i.i.d.) observations and control for cluster-specific unobservables by using nonlinear multi-level models, considering that refugees form unique networks in their resettlement regions and actively interact with one another within their clusters. Due to the binary dependent variable of this study, the incidental parameters problem is also taken into account. The multi-level estimates of this paper suggest that the September 11 attacks did not uniformly shock all sub-populations of refugees: rather, they presented a unique, substantial opportunity for Asian refugees and a serious threat to African and Arab refugees. One unanticipated finding is that the employment probability of European refugees remained stable, whereas that of Asian refugees markedly increased after the attacks. However, in terms of employment quality, measured by real wages, European refugees were the only ones who benefited from the attacks. Possible explanations for such heterogeneous impacts and different patterns of benefits are discussed, including positive versus negative selection into employment.

Similar content being viewed by others
Notes
The September 11 attacks were a series of airline hijackings and suicide attacks committed by 19 militants associated with Al-Qaeda against targets in the U.S., the deadliest terrorist attacks on American soil. Some 2750 people were killed in New York, 184 at the Pentagon, and 40 in Pennsylvania. Al-Qaeda is a militant Sunni Islamist multi-national organization and operates as a network of Islamic extremists and Salafist jihadists.
Full details on nonlinear multi-level econometric methods are discussed in Appendix A.1.
For the sake of brevity, additional robustness checks are presented in Online Supplement B.3.
The perpetrators of the September 11 attacks were 19 men from African or Arab countries who were affiliated with Al-Qaeda.
The empirical study of Ceritoglu et al. (2017) argues that Syrian refugees have negatively affected the employment outcomes of natives in Turkey. However, the labor market of Turkey is distinct from that of the U.S. primarily due to the level of its economic development and the prevalence of informal employment.
Such an argument is called nonnative-native complementarities in production (Ruist 2013).
The negative selection hypothesis argued by Borjas (1987) and corroborated by Rooth and Saarela (2007) and Moraga (2011), which claims that it is the lowest-wage, less skilled men who exhibit a stronger tendency to migrate, holds only in the case economic migrants (i.e., selection into migration) whose purpose of migration is wealth maximization.
Also, as previously mentioned in Sect. 2, the fact that all individuals in the data set are refugees obviates the need to consider the elasticity of the labor supply, making the analysis less complicated.
For more details on what to cluster over, see Sect. 4.2.
One caveat that needs to be mentioned is that the variable of the September 11 attacks is dichotomous and coded one for those whose 90-day job search periods were affected by the attacks regardless of the number of affected days. However, this matter is not considered serious in the context of this study because the variables of primary interest are the interaction terms between the attacks variable and the ethnicity variables. Debatable observations are those whose 90-day job search periods started between June 14, 2001 (i.e., one day was affected by the attacks) and September 10, 2001 (i.e., 89 days were affected by the attacks), and it is unlikely that there is a systematic difference in terms of the number of such debatable observations depending on a refugee’s ethnicity.
Females’ labor supply decisions are more difficult to compare due to their varying patterns of selection into work. For details, see Neal (2004), Blau et al. (1990s), Mulligan and Rubinstein (2008), and Olivetti and Petrongolo (2008). Especially, Neal (2004) underlines that relationships between labor force participation and family structure differ notably by ethnicity in the case of females, which can lead to non-comparable selection-into-employment patterns.
One exception is the linear probability model.
Whether this requirement is satisfied or not was tested by exploiting that the data set segregates the periods before the September 11 attacks into three quarters, with which the time trends for each ethnic subgroup before the attacks can be compared. The null hypothesis of the same time trends before the attacks could not be rejected.
It is assumed throughout this paper that \(N_{c}\) is exogenous.
For more details on this facet, see Cameron and Miller (2015).
See, among others, Pendergast et al. (1996) for an overview of the extensive literature on nonlinear multi-level models in biostatistics.
If this assumption is expected to be violated, the model should become more flexible by additionally including cluster-specific random slopes in addition to random intercepts, which can cause a greater computational burden.
For details on the linear probability model, see Appendix A.1.3.
For example, the Equal Employment Opportunity (EEO) laws collect such information in order to prohibit specific types of job discrimination in certain workplaces.
Year-specific dummies turn out to be both marginally and jointly insignificant , and the inclusion of year dummies does not substantially affect the estimation results. For a comparison, see Table 15 in Online Supplement B.4.
This is because a hypothesis tested, in the case of marginal effects, is about a function of all coefficients (Greene 2002).
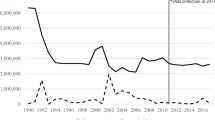
Figure 1 is based on those who had some job experiences in their home countries, completed secondary education and could speak English at an intermediate level when entering the U.S.. These features form one of the most common types that we can think of for job-seeking refugees.
The question asked whether a respondent thinks the number of immigrants from foreign countries who are permitted to come to the U.S. to live should be decreased.
This paper considers a region to be non-friendly toward immigration if more than 40% of respondents say that they think the number of immigrants to the U.S. should be limited.
The selection parameter \(\rho \) was estimated to be very close to zero from a magnitude standpoint along with its statistical insignificance.
For details on the initial resettlement support from the US government, see Online Supplement B.1.
In this context, selection refers to selection on unobservables.
The selection parameter of Asian refugees cannot be solely estimated due to the non-convergence of the maximum likelihood function.
In plain terms, \(\widetilde{B}_{c}\) indicates all possible combinations of 0 and 1 given \(N_{c}\overline{y}_{c}\).
In (14), it is assumed that the projection error \(w_{c}\) has zero mean and is uncorrelated with \(\overline{\mathbf {x}}_{c}\).
The modification in (25) is based on the key feature of maximum likelihood estimation that an overall (i.e., joint) likelihood function is the product of individual (i.e., marginal) probability density functions (Greene 2002; Baltagi 2011). In this context, individuals are categorized into two groups: \(S=1\) and \(S=0\).
\(\varvec{\gamma }_{d}\) and \(\varvec{\gamma }_{w}\) correspond to \(\varvec{\beta }_{d}\) and \(\varvec{\beta }_{w}\), respectively.
References
Åslundslund O, Rooth DO (2005) Shifts in attitudes and labor market discrimination: Swedish experiences after 9–11. J Popul Econ 18(4):603–629
Abadie A, Athey S, Imbens GW, Wooldridge J (2017) When should you adjust standard errors for clustering? Working Paper No. 24003, National Bureau of Economic Research
Amemiya T (1985) Advanced econometrics. Harvard University Press, Cambridge
Baltagi BH (2011) Econometrics. Springer, Berlin
Beaman LA (2012) Social networks and the dynamics of labour market outcomes: evidence from refugees resettled in the U.S. The Rev Econ Stud 79(1):128–161
Beck N (2020) Estimating grouped data models with a binary-dependent variable and fixed effects via a logit versus a linear probability model: The impact of dropped units. Polit Anal 28(1):139–145
Bera AK, Jarque CM, Lee LF (1984) Testing the normality assumption in limited dependent variable models. Int Econ Rev 25(3):563–578
Blau FD, Kahn LM (1990s) The U. S. gender pay gap in the 1990s: slowing convergence. Ind Labor Relat Rev 60(1):45–66
Blundell R, MaCurdy T (1998) Labor supply. In: Handbook of labor economics, vol 3, Elsevier, pp 1559–1695
Blundell R, Gosling A, Ichimura H, Meghir C (2007) Changes in the distribution of male and female wages accounting for employment composition using bounds. Econometrica 75(2):323–363
Bonanno GA, Jost JT (2006) Conservative shift among high-exposure survivors of the september 11th terrorist attacks. Basic Appl Soc Psychol 28(4):311–323
Borjas GJ (1987) Self-selection and the earnings of immigrants. Am Econ Rev 77(4):531–553
Braakmann N (2009) The impact of september 11th, 2001 on the employment prospects of Arabs and Muslims in the German labor market. J Econom Stat 229(1):2–21
Browne WJ, Draper D (2006) A comparison of Bayesian and likelihood-based methods for fitting multilevel models. Bayesian Anal 1(3):473–514
Brumback BA, Dailey AB, Brumback LC, Livingston MD, He Z (2010) Adjusting for confounding by cluster using generalized linear mixed models. Stat Probab Lett 80(21):1650–1654
Burawoy M (1976) The functions and reproduction of migrant labor: comparative material from southern Africa and the united states. Am J Soc 81(5):1050–1087
Cameron AC, Miller DL (2015) A practitioner’s guide to cluster-robust inference. J Hum Resour 50(2):317–372
Cameron AC, Trivedi PK (2005) Microeconometrics. Cambridge Press, Cambridge
Cameron AC, Trivedi PK (2009) Microeconometrics using Stata. Stata Press, College Station
Ceritoglu E, Yunculer HBG, Torun H, Tumen S (2017) The impact of Syrian refugees on natives’ labor market outcomes in turkey: evidence from a quasi-experimental design. IZA J Labor Policy 6(1):5
Chamberlain G (1980) Analysis of covariance with qualitative data. Rev Econ Stud 47(1):225–238
Dagnelie O, Mayda AM, Maystadt JF (2019) The labor market integration of refugees to the united states: do entrepreneurs in the network help? Eur Econ Rev 111:257–272
Damm AP (2009a) Determinants of recent immigrants’ location choices: quasi-experimental evidence. J Popul Econ 22(1):145–174
Damm AP (2009b) Ethnic enclaves and immigrant labor market outcomes: quasi-experimental evidence. J Labor Econ 27(2):281–314
Damm AP (2014) Neighborhood quality and labor market outcomes: evidence from quasi-random neighborhood assignment of immigrants. J Urban Econ 79:139–166
D’Amuri F, Ottaviano GI, Peri G (2010) The labor market impact of immigration in Western Germany in the 1990’s. Eur Econ Rev 54(4):550–570
Dustman C, Vasiljeva K, Damm AP (2019) Refugee migration and electoral outcomes. Rev Econ Stud 86(5):2035–2091
Dávila A, Mora MT (2005) Changes in the earnings of Arab men in the US between 2000 and 2002. J Popul Econ 18(4):587–601
Edin PA, Fredriksson P, Åslundslund O (2003) Ethnic enclaves and the economic success of immigrants: evidence from a natural experiment. Q J Econ 118(1):329–357
Evans MDR, Kelley J (1991) Prejudice, discrimination, and the labor market: attainments of immigrants in Australia. Am J Sociol 97(3):721–759
Foged M, Peri G (2016) Immigrants’ effect on native workers: new analysis on longitudinal data\(\dagger \). Am Econ J Appl Econ 8(2):1–34
Ford CA, Udry J, Gleiter K (2001) Chantala K (2003) Reactions of young adults to september 11. J Adolesc Health 32(2):124–125
Friedberg RM, Hunt J (1995) The impact of immigrants on host country wages, employment and growth. J Econ Perspect 9(2):23–44
Greene WH (2002) Econometric analysis. Pearson Education, London
Greene WH (2007) Discrete choice modeling. In: Palgrave handbook of econometrics, Springer, pp 473–556
Gronau R (1974) Wage comparisons —a selectivity bias. J Polit Econ 82(6):1119–1143
Guo G, Zhao H (2000) Multilevel modeling for binary data. Rev Sociol 26(1):441–462
Hall DB, Severini TA (1998) Extended generalized estimating equations for clustered data. J Am Stat Assoc 93(444):1365–1375
Hamerle A, Ronning G (1995) Panel analysis for qualitative variables pp 401–451
Hausman JA (1978) Specification tests in econometrics. Econometrica 46(6):1251–1272
Heckman JJ (1974) Shadow prices, market wages, and labor supply. Econometrica pp 679–694
Heckman JJ (1979) Sample selection bias as a specification error. Econometrica 47(1):153–161
Hersh ED (2013) Long-term effect of september 11 on the political behavior of victims’ families and neighbors. Proc Nat Acad Sci USA 110(52):20959–20963
Hosmer DW Jr, Lemeshow S, Sturdivant RX (2013) Applied logistic regression, vol 398. Wiley, London
Huddy L, Feldman S (2011) Americans respond politically to 9/11: understanding the impact of the terrorist attacks and their aftermath. Am Psychol 66(6):455–467
Huddy L, Feldman S, Taber C, Lahav G (2005) Threat, anxiety, and support of antiterrorism policies. Am J Polit Sci 49(3):593–608
Jost JT, Glaser J, Kruglanski AW, Sulloway FJ (2003) Political conservatism as motivated social cognition. Psychol Bull 129(3):339–375
Karaca-Mandic P, Norton EC, Dowd B (2012) Interaction terms in nonlinear models. Health Serv Res 47:255–274
Kaushal N, Kaestner R, Reimers CW (2007) Labor market effects of September 11th on Arab and Muslim residents of the United States. J Hum Resour 42(2):275–308
Keane M, Moffitt R, Runkle D (1988) Real wages over the business cycle: estimating the impact of heterogeneity with micro data. J Polit Econ 96(6):1232–1266
Killingsworth MR (1983) Labor supply. Cambridge Press, Cambridge
Kleinman LC, Norton EC (2009) What’s the risk? a simple approach for estimating adjusted risk measures from nonlinear models including logistic regression. Health Serv Res 44(1):288–302
Lancaster T (2000) The incidental parameter problem since 1948. J Econom 95(2):391–413
Manacorda M, Manning A, Wadsworth J (2012) The impact of immigration on the structure of wages: theory and evidence from Britain. J Eur Econ Assoc 10(1):120–151
Moffitt RA (1999) New developments in econometric methods for labor market analysis. In: Handbook of labor economics 3:1367–1397
Moraga JFH (2011) New evidence on emigrant selection. Rev Econ Stat 93(1):72–96
Mroz TA (1987) The sensitivity of an empirical model of married women’s hours of work to economic and statistical assumptions. Econometrica 55(4):765–799
Mulligan CB, Rubinstein Y (2008) Selection, investment, and women’s relative wages over time. Q J Econ 123(3):1061–1110
Mundlak Y (1978) On the pooling of time series and cross section data. Econometrica 46(1):69–85
Munshi K (2003) Networks in the modern economy: Mexican migrants in the U. S. labor market. Qu J Econ 118(2):549–599
Neal D (2004) The measured black–white wage gap among women is too small. J Polit Econ 112(S1):S1–S28
Neuhaus JM, Kalbfleisch J (1998) Between- and within-cluster covariate effects in the analysis of clustered data. Biometrics 54(2):638–645
Neuhaus JM, McCulloch CE (2006) Separating between- and within-cluster covariate effects by using conditional and partitioning methods. J R Stat Soc B 68(5):859–872
Neyman J, Scott EL (1948) Consistent estimates based on partially consistent observations. Econometrica 16(1):1
Olivetti C, Petrongolo B (2008) Unequal pay or unequal employment?: a cross-country analysis of gender gaps. J Labor Econ 26(4):621–654
Ottaviano GIP, Peri G (2012) Rethinking the effects of immigration on wages. J Eur Econ Assoc 10(1):152–197
Pendergast JF, Gange SJ, Newton MA, Lindstrom MJ, Palta M, Fisher MR (1996) A survey of methods for analyzing clustered binary response data. Int Stat Rev 64(1):89–118
Pepper JV (2002) Robust inferences from random clustered samples: an application using data from the panel study of income dynamics. Econ Lett 75(3):341–345
Peri G (2007) Immigrants’ complementarities and native wages: Evidence from california. National Bureau of Economic Research
Peri G (2011) Rethinking the area approach: immigrants and the labor market in California. J Int Econ 84(1):1–14
Peri G (2014) Do immigrant workers depress the wages of native workers? The IZA World of Labor pp 1–42
Piore MJ (1980) Birds of passage. Cambridge University Press, Cambridge
Rabby F, Rodgers WM (2011) Post 9–11 U.S. Muslim labor market outcomes. Atl Econ J 39(3):273–289
Rodriguez G, Goldman N (2001) Improved estimation procedures for multilevel models with binary response. J R Stat Soc Ser A 164(2):339–355
Rooth DO, Saarela J (2007) Selection in migration and return-migration: evidence from micro data. Econ Lett 94(1):90–95
Ruist J (2013) Immigrant-native wage gaps in time series: complementarities or composition effects? Econ Lett 119(2):154–156
Schüller S (2016) The effects of 9/11 on attitudes toward immigration and the moderating role of education. Kyklos 69(4):604–632
Sheridan LP (2006) Islamophobia pre- and post-september 11th, 2001. J Interpers Violence 21(3):317–336
Singh A (2002) We are Not the Enemy: Hate Crimes Against Arabs, Muslims, and Those Perceived to be Arab Or Muslim After September 11, vol 14. Human Rights Watch
Smith JP, Ward M (1989) Women in the labor market and in the family. J Econ Perspect 3(1):9–23
Snijders TAB, Berkhof J (2008) Diagnostic checks for multilevel models. Handbook of Multilevel Analysis pp 141–175
Tobin J (1958) Estimation of relationships for limited dependent variables. Econometrica 26(1):24
Topa G (2001) Social interactions, local spillovers and unemployment. Rev Econ Stud 68(2):261–295
Widner D, Chicoine S (2011) It’s all in the name: employment discrimination against Arab Americans. Sociol Forum 26(4):806–823
Wooldridge JM (2003) Cluster-sample methods in applied econometrics. Am Econ Rev 93(2):133–138
Wooldridge JM (2010) Econometric analysis of cross section and panel data. MIT Press, Cambridge
Acknowledgements
I thank the editor, the associate editor, and two anonymous referees for their careful reading and helpful suggestions despite the long-lasting pandemic situation. Earlier versions of this article benefited from comments by Horst Entorf, Nicola Fuchs-Schündeln, Cornelia Storz (U. Frankfurt), Jin-Young Choi (Xiamen U.), Jo-Yup Ahn, Yoon-Gyu Yoon, Jae-Min Seong (KLI), Le Van Cuong (U. Paris I), Marie Lalanne (Università degli Studi di Torino), and numerous participants at conferences including the Econometric Society Meetings in 2019. I thank Birgit Herrmann for excellent administrative assistance and gratefully acknowledge various support from the Federal Government of Germany, Frankfurter Wirtschaftswissenschaftliche Gesellschaft, Development and Policies Research Center, and the French National Center for Scientific Research (CNRS).
Funding
None
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
I, as the author of this manuscript, certify that I have no conflict of interest to declare at the time of submission.
Ethical approval
This study does not contain any studies with human participants or animals performed by the author.
Data availability
The data that support the findings of this study are not publicly available but are available from the International Rescue Committee upon request. Restrictions apply to the availability of these data according to the relevant regulations of the US government.
Code availability
The program codes that generate the final results of this study are available from the author upon request.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary material
Below is the link to the electronic supplementary material.
A Appendix
A Appendix
1.1 A.1 Details on multi-level econometric models
1.1.1 A.1.1 Conditional maximum likelihood model
In general, the fixed effects model is considered more conservative in that it allows for the possible correlation between cluster-specific fixed effects \(\alpha _{c}\) and covariates. However, nonlinear maximum likelihood variants of the cluster-specific fixed effects model entail further complications—especially in the case of data with a small number of cluster members \(N_{c}\). This is because data with small \(N_{c}\) have the problem of too many incidental parameters (i.e., \(\alpha _{1},\ldots ,\alpha _{C}\)), while the number of observations for estimating each \(\alpha _{c}\) is not enough (Neyman and Scott 1948). Unlike linear cases, it is generally not possible to eliminate such nuisance parameters in nonlinear cases (Hall and Severini 1998). This is the reason why the present study, the dependent variable of which is binary, cannot simply use the dummy variable fixed effects model. Cluster-specific dummies, in nonlinear cases with the finite number of cluster members \(N_{c}\), fail to properly pick up \(\alpha _{c}\) and render maximum likelihood estimates inconsistent (Neyman and Scott 1948; Chamberlain 1980; Lancaster 2000; Greene 2002).
One alternative method for obtaining consistent estimates that eliminates unwanted \(\alpha _{c}\) is using the conditional maximum likelihood model (CML). It is based on a log density for the jth individual (in the cth cluster) that conditions on \(\sum _{j=1}^{N_{c}}y_{jc}\), which refers to the total number of outcomes equal to one (i.e., employed) for a given cluster (Chamberlain 1980). When a binary logit model with cluster fixed effects \(\alpha _{c}\) specifies
where all notations are the same as defined in Section 4, the joint conditional probability for the cth cluster is calculated as follows:
where \({\widetilde{B}_{c}=\{(d_{1c},d_{2c},d_{3c},\ldots ,d_{N_{c}c})\mid d_{jc}=0}\,\text {or}\,{1,}\,\text {and}\,{\sum _{j=1}^{N_{c}}d_{jc}=\sum _{j=1}^{N_{c}}}y_{jc}{=N_{c}\overline{y}_{c}\}}\) (Hamerle and Ronning 1995; Cameron and Trivedi 2009; Hosmer et al. 2013).Footnote 31 This approach is uniquely possible only with logit by virtue of its feature that \(\exp (\cdot )\) appears both in the numerator and in the denominator, which enables two sets of common factors — \(\exp (\sum _{j=1}^{N_{c}}y_{jc}\mathbf {i}_{c}^{\prime }\varvec{\eta })=\exp (\sum _{j=1}^{N_{c}}d_{jc}\mathbf {i}_{c}^{\prime }\varvec{\eta })\) and \(\exp (\sum _{j=1}^{N_{c}}y_{jc}\alpha _{c})=\exp (\sum _{j=1}^{N_{c}}d_{jc}\alpha _{c})\) conditioning on \(N_{c}\overline{y}_{c}\) — to be canceled out in (12).Footnote 32 Finally, the conditional likelihood is \(\prod _{c=1}^{C}\Pr _{c}(y_{1c},y_{2c},y_{3c},\ldots ,y_{N_{c}c}\mid N_{c}\overline{y}_{c})\), the product of (12) over all C clusters, where C refers to the total number of clusters.
Under the between-cluster independence assumption and the conditional independence assumption (CIA) that within-cluster observations \(\{y_{1c},y_{2c},y_{3c},\ldots ,y_{N_{c}c}\}\) are independent conditioning on \(\mathbf {v}_{jc}\), \(\mathbf {i}_{c}\), and \(\alpha _{c}\), the conditional maximum likelihood model eliminates \(\alpha _{c}\) and yields consistent coefficient estimates of level-one covariates \(\mathbf {v}_{jc}\) (Chamberlain 1980). The primary advantage of the conditional maximum likelihood model resides in the fact that it does not rely on any assumptions concerning the distribution of \(\alpha _{c}\). This approach is referred to as the Chamberlain’s fixed effects logit model in econometrics and applicable even when cluster sizes vary.
While eliminating \(\alpha _{c}\) in (12) is uniquely feasible without the incidental parameters problem, this approach, however, still entails some substantial problems, the most critical point of which lies in the fact that it leads to the loss of observations if \(y_{jc}\) is either 0 for all j or 1 for all j. On top of this, all clusters with \(N_{c}=1\) are excluded, further impairing efficiency (Cameron and Trivedi 2005). Moreover, while this method is useful for obtaining consistent coefficient estimates, it is generally not possible to estimate additive marginal effects because they depend on eliminated \(\alpha _{c}\), unlike linear fixed effects models (Beck 2020). Some researchers report marginal effects evaluated at a certain value \(\alpha _{c}=q\): however, that is not much meaningful as where to evaluate \(\alpha _{c}\) is a completely arbitrary decision. As an alternative, a common way of interpreting coefficients is using an odds ratio, which measures the probability of \(y=1\) relative to the probability of \(y=0\). However, such multiplicative interpretation is usually less intuitive than additive marginal effects. This is the point at which the more flexible random effects model should also be considered.
1.1.2 A.1.2 Chamberlain–Mundlak’s correlated random effects probit model
When the simplest model \(y_{jc}=\mathbf {x}_{jc}^{\prime }\varvec{\beta }+u_{jc}\) is supposed with the error term decomposition \(u_{jc}=\alpha _{c}+\varepsilon _{jc}\), the conventional random effects model assumes
and this is undeniably a very strong assumption. It should be carefully noted that (13) requires two conditions to be satisfied concurrently: first, \(\alpha _{c}\) and \(\mathbf {x}_{jc}\) should not be correlated, and second, \(\alpha _{c}\) should be normally distributed with homoskedasticity (i.e., constant variance \(\sigma _{\alpha }^{2}\)).
Due to the implausibility of the assumption (13) in the case of the data under investigation, this study does not use the conventional random effects model; instead, the approach of Chamberlain (1980) is leveraged to clustered observations, which had been originally devised in the context of panel data. Based on the method of Chamberlain (1980), the correlation between \(\alpha _{c}\) and \(\mathbf {x}_{jc}\) can be tolerated by replacing \(\alpha _{c}\) with its linear projection onto the cluster-specific means of covariates (i.e., \(\overline{\mathbf {x}}_{c}\)) including a projection error (Wooldridge 2010). By allowing \(\alpha _{c}\) to be determined by \(\overline{\mathbf {x}}_{c}\), \(\alpha _{c}\) can be expressed as
where \(w_{c}\) denotes the projection error.Footnote 33 Then, the Mundlak (1978) version of Chamberlain’s assumption can be written as
This signifies that \(\alpha _{c}\) can be correlated with regressors through \(\overline{\mathbf {x}}_{c}\): therefore, the inclusion of \(\overline{\mathbf {x}}_{c}\) is expected to control for the correlation between cluster-specific heterogeneous features and covariates. However, this assumption (15), albeit more flexible than (13), is still restrictive in that it specifies the conditional distribution of \(\alpha _{c}\). In plain terms, (15) means that \(\alpha _{c}\) given \(\mathbf {x}_{jc}\) should be normally distributed with mean \(\psi +\overline{\mathbf {x}}_{c}^{\prime }\varvec{\xi }\) and variance \(\sigma _{w}^{2}\).
While the fundamental logic of Mundlak (1978) is to let \(\overline{\mathbf {x}}_{c}\) in (14) include all regressors, within-cluster invariant regressors do not provide any information for this projection. Hence, regressors are categorized into two types: within-cluster variant regressors \(\mathbf {v}_{jc}\) and within-cluster invariant regressors \(\mathbf {i}_{c}\), as previously mentioned with (3) in Sect. 4. Considering this separation, cluster-specific \(\alpha _{c}\) can be rewritten as
where \(\overline{\mathbf {v}}_{c}\) refers to the averages of level-one covariates \(\mathbf {v}_{jc}\) within each cluster. Naturally, cluster-invariant level-two covariates \(\mathbf {i}_{c}\) are still included as exploratory variables. As a result, the generalized linear model along with probit as a binary link function can be defined as
where \(\Phi \) denotes the standard normal cumulative distribution function. This method is called the Chamberlain–Mundlak’s correlated random effects probit model (CRE). The test of \(\varvec{\tau }=0\) in (17), which is known as the Mundlak test, can be easily implemented in a bid to figure out whether the assumption of the conventional random effects model (13) is valid (i.e., if \(\varvec{\tau }=0\)) or not (i.e., if \(\varvec{\tau }\ne 0\)) (Mundlak 1978). The results of the test applied to this study are discussed in Online Supplement B.2.
The Chamberlain–Mundlak’s correlated random effects probit model yields unbiased estimates of level-one covariates (Mundlak 1978; Neuhaus and Kalbfleisch 1998; Snijders and Berkhof 2008). Hence, this study also uses the Chamberlain–Mundlak’s correlated random effects probit model along with the conditional maximum likelihood model.
1.1.3 A.1.3 Linear probability model with cluster fixed effects
As previously mentioned in Sect. 4.3, if we use the identity link for g in (7), the simple linear probability model with cluster fixed effects can be defined as shown below.
Despite its simplicity and computational convenience, the simple linear probability model with cluster fixed effects has some shortcomings as follows. First, the linear probability model, which uses neither a cumulative distribution function nor a latent variable model, has no structural room for error terms. Second, some predicted probabilities based on the linear probability model may have nonsensical values that are less than zero or greater than one (i.e., outside the unit interval). Third, the linear probability model can even lead to negative variances (Greene 2002).
However, on a more positive note, the linear probability model requires no distributional assumptions of disturbances, the violation of which can make maximum likelihood estimates inconsistent (Bera et al. 1984). Hence, this study also uses the linear probability model for comparisons. It is also used when a maximum likelihood function fails to converge because of the large number of parameters to be estimated.
1.2 A.2 Bivariate selection model
Conventional selection models are composed of two sequential equations—one for employment (i.e., also often called selection or participation) and the other for wage outcomes (Amemiya 1985). An employment equation with binary outcomes can be expressed as shown below, where \(y_{d}^{*}\) is a latent variable that determines whether to work or not.
While Cameron and Trivedi (2005) explains that \(y_{d}^{*}\) is construed as the unobserved desire or propensity to work, Heckman (1974), from a labor supply standpoint, notes that it can be regarded as the difference between a refugee’s market wage (i.e., wage offer) and his or her reservation wage. On the other hand, a resultant market wage equation with continuous outcomes can be expressed as follows, where latent \(y_{w}^{*}\) determines how much to work.
The market wage equation (20) denotes that the wage outcome of a refugee is observed if and only if a refugee is employed (i.e., \(y_{d_{i}}^{\text {Employment}}=1\)) with \(y_{d_{i}}^{*}>0\) in (19). In other words, whether we can observe a refugee’s market wage level or not entirely depends on his or her labor supply decision. The canonical approach for modeling selection specifies linear models with additive error terms in the following manner (Cameron and Trivedi 2005).
The correlation between \(\varepsilon _{d}\) and \(\varepsilon _{w}\) in (21) is the core of sample selection models, which, if overlooked, can cause problems in estimating \(\varvec{\beta }_{w}\) (Greene 2002). In the case of the bivariate sample selection model, suggested by Tobin (1958), estimation by maximum likelihood is straightforward given the additional assumption of
which, in plain terms, means that the correlated errors are joint normally distributed with homoskedasticity (Cameron and Trivedi 2005).Footnote 34 Gronau (1974), Heckman (1979), and Keane et al. (1988) are among previous studies using this bivariate normality assumption: for further details on this assumption, see Amemiya (1985) and Moffitt (1999). Based on the assumption (22), the bivariate sample selection model maximizes the likelihood function
and the use of probit as a link function leads to
where \(\rho \) refers to the correlation coefficient between \(\varepsilon _{d}\) and \(\varepsilon _{w}\). As is customary, \(\Phi \) denotes the standard normal cumulative distribution function, whereas \(\phi \) is the standard normal probability density function. The log of (24) is the objective function of the bivariate sample selection model. However, in this context, the selection parameter of European refugees and that of non-European refugees should be separately estimated, and if they are estimated in a single likelihood function, they can be directly compared. Therefore, (24) is modified as follows.
While all notations are the same as defined hitherto, \(S_{i}=1\) means that an individual i is a European refugee (i.e., \(i\in S\)).Footnote 35 Thus, \(\rho _{1}\) refers to the correlation between \(\varepsilon _{d}\) and \(\varepsilon _{w}\) of European refugees, and \(\sigma _{1}\) denotes the standard deviation of European refugees’ \(\varepsilon _{w}\). Likewise, \(\rho _{2}\) refers to the correlation between \(\varepsilon _{d}\) and \(\varepsilon _{w}\) of non-European refugees, and \(\sigma _{2}\) denotes the standard deviation of non-European refugees’ \(\varepsilon _{w}\). The likelihood function (25) is flexible in the sense that the coefficients of \(\mathbf {x}_{d}\) and \(\mathbf {x}_{w}\) are allowed to be different in those two groups (i.e., \(\varvec{\beta }_{d}\), \(\varvec{\beta }_{w}\), \(\varvec{\gamma }_{d}\), \(\varvec{\gamma }_{w}\)).Footnote 36
Rights and permissions
About this article
Cite this article
Shin, S. Were they a shock or an opportunity?: The heterogeneous impacts of the 9/11 attacks on refugees as job seekers—a nonlinear multi-level approach. Empir Econ 61, 2827–2864 (2021). https://doi.org/10.1007/s00181-020-01963-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00181-020-01963-8
Keywords
- Refugee labor market
- Clustered observations
- Nonlinear multi-level models
- Chamberlain–Mundlak’s correlated random effects probit model
- Conditional logit fixed effects model