Education, income and happiness: panel evidence for the UK

Abstract

Using panel data from the BHPS and its Understanding Society extension, we study life satisfaction (LS) and income over nearly two decades, for samples split by education, and age, to our knowledge for the first time. The highly educated went from lowest to highest LS, though their average income was always higher. In spite of rapid income growth up to 2008/2009, the less educated showed no rise in LS, while highly educated LS rose after the crash despite declining real income. In panel LS regressions with individual fixed effects, none of the income variables was significant for the highly educated.

1 Introduction

Education is correlated with both income and health—each of which, in turn, has a positive effect on life satisfaction (LS). Those with higher education generally have access to more interesting and better-paid jobs, together with other non-pecuniary benefits. Meanwhile, manual labour is systematically correlated with lower LS—so it is not surprising that (higher) education is generally considered to be beneficial for subjective well-being, happiness or LS, as well as for objective individual economic and social goals. Thus, in their wide-ranging, cross-country survey of ‘Happiness at Work’ based on Gallup World Poll data, De Neve and Ward (2017) find a highly significant, positive effect of high education on LS in the presence of many other relevant controls such as health, income and employment—although a gender split for a much smaller sample based on European Social Survey data then indicates that a similar effect is only evident for men.

It is, therefore, initially rather surprising that a previous study of LS with British Household Panel Survey (BHPS) data found negative or insignificant effects of higher education in various specifications with numerous controls, while the positive effect was robust in German SOEP data (FitzRoy et al. 2014). However, using only Wave 1 BHPS data, Clark and Oswald (1996) report a negative relationship between a more specific job satisfaction variable and both education and comparison income. Via analysis of Wave 6–14 of the BHPS data, Powdthavee (2010) shows mainly negative estimates for education controls in pooled OLS estimation of LS and insignificant estimates for fixed-effects estimation. Green (2011) finds a negative effect of higher education on LS with Australian (HILDA) data using many controls, but Nikolaev and Rusakov (2016) find that higher education has a positive and increasing effect on LS from about the age of 35 in the same data set. Nikolaev (2016) also reports generally positive associations of education with various components of LS with the same data. Adding to conflicting results from HILDA, Powdthavee et al. (2015) estimate a structural model of education and life satisfaction and conclude that the direct effect of education is negative, while positive associations arise from the well-known positive effects of education on income and health. Overall, the existing literature contains mixed findings.

Here, we consider the UK over a rather longer time series. We extend the BHPS panel with the corresponding component of the Understanding Society data set (part of which involves individuals drawn from the BHPS) to study the development of life satisfaction (LS) and income across a couple of decades, in different education (and age) groups. Real household income (deflated by the Consumer Prices Index¹) was always highest for the highly educated and for all groups grew substantially in the 10 years up to the financial crash of 2008/2009. The subsequent decline and partial recovery were steepest for the highly educated. That group also saw a rise in average household size around the time of the crash, whereas the households of the least educated tended to become smaller.

LS, on the other hand, rose fastest for the highly educated from a surprising lowest to being highest among the education groups, a significant increase over a period when the proportion of highly educated roughly doubled. LS declined steeply for the low education group up to and beyond the crash, in spite of their rising income. Overall, average LS declined pre-crash despite rapid income growth. Except for the highly educated before the crash, whose income and LS both increased, these results contradict standard economic growth theories, but are consistent with the Easterlin paradox found in macro data. Of course, mainly negative correlations of averages are no guarantee of the sign of the average of LS–income correlations at the individual level—in general terms, this point can be traced back at least to Robinson (1950), and the coining of the term ‘ecological fallacy’ in Selvin (1958).

Various additional details emerge when we split the samples by age—specifically, for those aged under 45, and for those aged 45+. The LS of the younger, high education group overtook the rest by Wave 8 (1998/1999), while in the older group, LS only overtook the rest after the crash of 2008/2009 (in Wave 19), while relative incomes were similar. The older low educated suffered the steepest decline of LS over the whole period—from 5.40 (Wave 6) to 5.12 (Wave 23).

Easterlin’s (1974) seminal paper found no correlation between long-term economic growth in rich countries, and subjective well-being (SWB—evaluated in surveys of LS or happiness). With 40 years of additional data, and economic growth, there is little evidence of any generally increasing SWB trend,² (even in some of the fastest growing developing countries such as China). However, there is a strong cyclical relationship between real GDP per capita and SWB, with unemployment being a major cause of unhappiness that moves with the cycle, and critics have usually failed to distinguish carefully between trend growth and deviations from the trend (Easterlin 2013). Confirming and explaining these results, on the basis of ‘loss-aversion’, De Neve et al. (2014) show that economic downturns have negative effects on SWB which are several times the magnitude of the impact of longer periods of equivalent positive growth.

The paradox is deepened by the fact that richer people are generally happier than the poor in any one country at a given time, though many other factors such as health, family and employment are more important than income (but usually also correlated with income and education).³ The well-established importance of socio-economic status or relative income is often advanced as part of the explanation, but studies using only macro data on average happiness and per capita GDP obviously cannot explore this factor, while also omitting numerous important individual variables such as health, age and education, which do actually change in the aggregate over time. Other possible factors that could offset the benefits of growing average real incomes are rising inequality, reduced social mobility and the widely observed decline in many components of social capital, such as community, personal and family relationships, as well as security of employment—although these issues are beyond the scope of this paper. None of them seem to offer explanations for our surprising results. Adaptation to higher income was found to have only small effects by Layard et al. (2010).

It thus seems appropriate to use available large panel data sets, which follow individuals over time, to examine the effects of income (potentially, its level and growth) on their well-being, while controlling for both individual fixed effects and changing characteristics recorded in the survey data. Our main innovation here is to disaggregate the sample by three levels of education and by age. To the best of our knowledge, the education split in this context is a novel approach, which yields some really surprising results, including the lack of any significant own-or-comparison income effects on the LS of the highly educated, although their LS increased more than in other groups in the period. Another puzzle is why the high education group had lowest LS initially, but overtook the less educated to become most satisfied while higher education was rapidly expanding—see Blundell et al. (2016).

2 Data and methodology

Our main data are taken from Waves 6–10 and 12–18 of the British Household Panel Survey⁴ (BHPS), covering a period that runs from 1996/1997 to 2008/2009 (University of Essex, Institute for Social and Economic Research 2010) and from those parts of Waves 2–6 of the section of the new Understanding Society⁵ longitudinal study (Kantar Public, NatCen Social Research, University of Essex. Institute for Social and Economic Research 2016) that relate to active, consenting former members of the BHPS sample, covering a period⁶ from 2010–2011 to 2014–2015. An initial baseline of 214,704 observations is available, across the full income range. However, as is evident in Fig. 1, LS data were not collected for BHPS Wave 11 (17,609 observations for 2001/2002). Also evident from Fig. 1 (and its 95% confidence limits) is the fact that not all of the time variation in average LS can be attributed to sampling variation. For regression analysis, we generate results for up to 178,382 observations across 23,748 individuals, with those cases where there are missing values, and the highest income outliers,⁷ excluded. As usual, we note the deliberate over-sampling of the smaller nations of the UK since Wave 9—so that about half of the individuals in the BHPS are from Scotland, Wales and Northern Ireland,⁸ compared with less than 20% in the overall population.

Fig. 1

Life satisfaction, BHPS and Understanding Society (USoc), Waves 6–10, 12–23

A plausible hypothesis is that those with higher education, who generally have the best-paid and most interesting jobs, would be most likely to enjoy increasing life satisfaction with higher incomes, so we split the sample into three groups. For the initial BHPS waves, classification through the International Standard Classification of Education (ISCED) is available—and the split is into higher (ISCED categories 5a and 6—for first degrees and higher degrees), middle (ISCED categories 3a and 5b—for higher secondary and middle/higher vocational) and low (ISCED categories primary, low secondary and 3c—low secondary vocational) education. However, no ISCED codings are yet available for the Understanding Society waves—so that the three-way split had to be undertaken on the basis of a less sophisticated derived highest qualification variable.⁹ Since the crucial difference is the striking and quite counter-intuitive contrast between the higher and the two lower groups, we aggregate the latter pair to simplify Figs. 2, 3 and 4 (again, including confidence intervals) and our regressions.

Fig. 2

Life satisfaction by education, BHPS and USoc, Waves 6–10 and 12–23

Fig. 3

Life satisfaction by education, BHPS and USoc, aged < 45, Waves 6–10 and 12–23

Fig. 4

Life satisfaction by education, BHPS and USoc, aged 45+, Waves 6–10 and 12–23

Our estimation approach is quite similar to FitzRoy et al. (2014)—we use individual fixed effects in estimation of a LS equation with quite a number of controls—many of which are fairly standard when using BHPS data. These include marital status (including cohabiting), number of children, health status, education, labour market status, time spent in panel, whether year of last interview, log household size, age (via six age dummies to create seven age categories), housing ownership status, wave number and regions. We also tested the alternative of a traditional polynomial age specification—and found results quite similar to FitzRoy et al. (2014).

In Online Appendix, sample means are shown for many of the controls in Table A1a: the sample is also split by education level (see Fig. 5 as well). We also follow Moulton (1990) in recognising the potential (cluster related) effect of aggregate regressors on standard errors. Given that we are focusing on the estimation of individual-specific fixed-effects regressions, we assume clustering at the level of the individual.

Fig. 5

Education categories, BHPS and USoc, Waves 6–23

For the crucial test of the effects of income on LS in different education groups, we include (deflated) own household income (for the month before interview) and comparison (peer group) income separately. The definition used here for comparison income follows that employed by FitzRoy et al. (2014)—whereby comparison groups are defined by age bands (between 3 years younger and 6 years older), sex, education (two categories), region (three categories) and Wave. The groups are quite broad in specification—with a median cell size around 335 members, and a bottom decile at 80 members. We also experiment with the inclusion of upward and downward changes in own household income, allowing for asymmetric LS responses. In addition to including a full set of regional dummies (with Greater London as the reference region), we control for (the ILO measure¹⁰ of) regional unemployment—which is not exclusively cyclical, of course—as well as regional house prices.¹¹ The type of equation that is estimated—sometimes split by age range (under 45 and 45+, respectively) and sometimes split by education level (high vs. medium/low)—takes the following form, for the typical fixed-effects regression:

$$ {\text{LS}}_{it} = \beta_{0} + \beta_{1} \ln \bar{Y}_{jt} + \beta_{2} \ln Y_{it} + \beta_{3} \ln \left({\frac{{Y_{it}}}{{Y_{it - 1}}}} \right)^{+} + \beta_{4} \ln \left({\frac{{Y_{it - 1}}}{{Y_{it}}}} \right)^{-} + {\varvec{\alpha}} {\varvec{X}}_{it} + v_{i} + \varepsilon_{it}, $$

(1)

where the i subscript indexes the individual, the t subscript indexes the wave (year) of the panel data and j denotes the reference group (regarding individual i) for comparison income $\left( {\bar{Y}} \right)$. Household income is denoted Y, while the + and − superscripts capture, respectively, the cases where deflated household income rises (relative to the previous wave) or falls. The separate terms allow, firstly, for a baseline effect of household income on life satisfaction. This effect is expected to be positive, and since income is entered in log form, the declining positive marginal utility of raw real household income is reflected naturally by a positive coefficient. In addition, any impact on current life satisfaction from wave-to-wave changes in household income (and, potentially, asymmetry in the respective impacts of a given magnitude of rise and fall in household income) can also be captured. The X term captures a vector of additional included controls, with an attendant vector of estimated coefficients $\varvec{\alpha}$. The individual fixed effect is denoted v, while ε is the remaining disturbance term.

We also tested for any additional effects of regional gross value added (GVA) per capita, in unreported regressions. It is clear from Fig. 10 (“Appendix 1”) how different Greater London is, in this respect (as in many others) from the other UK NUTS1 regions. Like Pfaff and Hirata (2013), we found little systematic effect of regional GVA, which is not surprising given the inclusion of household income, and we also add comparison income. In contrast to their claims, this hardly supports Easterlin, since (on average) household incomes grow with macro income measures, and are closely related to LS in cross section, and in some of our panel results.

3 Results and discussion

Figure 1 demonstrates the lack of an obvious time trend in LS across Waves 6–18 of the BHPS¹²—although, within the Understanding Society waves, there appears to be some evidence of a lagged adverse reaction to the infamous Great Recession (itself evident via the real GVA per capita plots in Fig. 10). There is also a bounce-back in LS between Waves 22 and 23.

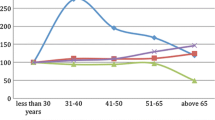
We present plots of LS by education in Figs. 2, 3 and 4, log real household income in Fig. 6 and normalised¹³ real household income by education in Figs. 7, 8 and 9. The most surprising message from these plots is that the highly educated (top 14% or so overall, but with a trend from 10% in Wave 6 to 15% in Wave 18 and 20% in Wave 23—as shown in Fig. 5) started with the lowest LS, but consistently have the highest LS from Wave 15 onwards (Fig. 2). This is despite the fact that the percentage growth (around 17%) in their average real household incomes over the period was very similar to those with medium and low education (17% and 18%) and, at 14% for equivalised income, below that for those with medium and low education (18 and 21%). An interesting further dimension is the expansion of the proportion of the UK population that are highly educated (see Fig. 5). Between BHPS Waves 6 and 18, this rose by 42% and 96% between BHPS Wave 6 and Wave 23 (Understanding Society Wave 6).¹⁴

Fig. 6

Log income, BHPS and USoc, Waves 6–23

Fig. 7

Normalised income by education, BHPS and USoc, Waves 6–23

Fig. 8

Normalised income by education, BHPS and USoc, aged < 45, Waves 6–23

Fig. 9

Normalised income by education, BHPS and USoc, aged 45+, Waves 6–23

Summary statistics are displayed for a few key variables in Table 1—split by education level. Overall, there is a tendency towards a positive link between LS and education level. There is a more noticeable (and expected) positive link between household income and education level, and this unsurprisingly is also reflected in comparison income. The decline in average age by education level is consistent with the known ongoing increase in access to higher levels of education in the UK, over the last couple of decades (and beyond).

Table 1 UK, BHPS and USoc, Waves 6–10 and 12–23

A further split of the sample into a younger group (those under 45 years) and an older group (those aged 45+) reveals that the positive relationship between LS and education level for the former is reversed for the latter. This can also be seen by examining Figs. 3 and 4, where the older highly educated have the lowest LS for most of the period. On the other hand, average household income (and also average comparison income) is robustly higher for an increase in education level, for both age groupings (see Tables 2 and 3; and also Figs. 8 and 9, on normalised income). For age itself within the younger group, the highly educated tend to be older—which is likely to be a reflection of the longer time taken to complete education to a high level. Meanwhile, there is a negative relationship between age and education level within the older age grouping, which provides further evidence that the incidence of high education is increasing among successive birth cohorts. This view is broadly supported by Figs. 11 and 12, although a switch from low to medium education is noticeable for both age groupings.¹⁵

Table 2 UK, BHPS and USoc, Waves 6–10 and 12–23

Table 3 UK, BHPS and USoc, Waves 6–10 and 12–23

Most of the compositional aspects in the data set are unsurprising. For instance, the highly educated group is drawn disproportionately from Greater London, South East England and Scotland. Its members are more likely to be employed, and less likely to be unemployed or to be long-term sick or disabled (across the full age range and on both sides of the age split). They are also less likely to rent their dwelling. Among those aged 45+, the highly educated are less likely to be retired and they enjoy a marked health advantage (present, to a lesser extent, in the younger age range too). Perhaps less obvious is the fact that the highly educated under 45 years have a lower average household size than the low or medium educated (maybe due in part to later marriage and starting of a family), but, among those aged 45+, the highly educated have the highest average household size—possibly linked to a lower proportion having been widowed.

Our first estimation results are in Table 4, containing estimates of LS fixed-effects regressions across all education levels—initially across the entire age range, and then for younger (< 45) and older (45+) subgroups. Controls for high education are included (among the long list of controls), with an interaction to allow for a differential impact of high education on LS from Wave 14 (2004/2005) onwards (in line with Fig. 2). We report only coefficients of the various income variables, plus those for the high education * Wave 14+ interaction. A positive interaction effect is indeed evident for Waves 14–23, but the overall effect of being highly educated across those waves is significant at the 5% level only for the 45+ age range.¹⁶ Own income and its upward changes have strong positive effects for the whole sample, and for those under 45 years taken alone. Meanwhile, comparison income has the positive, signalling effect for them that was found previously for those under 45 years¹⁷—but the effect is statistically insignificant in our case. The usual negative effect for comparison income is again found for those aged 45+, or for the whole sample across the entire age range. It should be noted that the number of individuals reported in the first column of Table 4, for the whole sample, cannot be expected to be the same as the sum of the totals in the other two columns (for the age split). This is because the observations for some individuals can be found on both sides of the age split boundary.

Table 4 Individual fixed effects, across education—UK, BHPS and USoc, Waves 6–10 and 12–23

Although the alternative of pooled cross-sectional estimation is problematic for our unbalanced panel data, we have included Table A2a in Online Appendix, for additional context—with standard errors clustered this time by the comparison income grouping regressor. This shows similar comparison income results to those found previously in Table 8 of FitzRoy et al. (2014)—with a significant negative estimate for the full age range and also for the 45+ sample. Estimates for own household income are also broadly in line with that earlier work.¹⁸ Moreover, unreported regressions across the whole age range with comparison income interacted with the age grouping control categories and own income interacted with an ‘aged 45+’ dummy generated chiefly similar results to those in Table 24 of FitzRoy et al. (2014), both for fixed-effects and for pooled OLS.

In Table 5, we report the same specification for the highly educated, with the really remarkable result that none of the standard income variables is significant for either age group (or across the full age range). Recall, from Fig. 2, that wave-specific LS arithmetic means rose significantly between BHPS Wave 6 and BHPS Wave 18 for the highly educated, while the number of highly educated individuals rose by 50% (Fig. 5). Figure 3 indicates an increase in LS for the younger age group among the highly educated, but no significant change for the older age group. The impact of the Great Recession did seem to push down LS somewhat across Waves 20–22, albeit with a bounce-back in Wave 23. These trends in LS must be due to other factors. Of our controls, a few do have statistically significant attached estimates. For the full age range, as expected, economic activity status categories such as employee, self-employed, retirement, family care and full-time education are all positive for LS, relative to unemployment, and long-term sickness or disability is negative. Being married or cohabiting is positive for LS, compared with being single and never married. Good health and bad health each have the expected impact on LS, compared with the baseline health category. Sampling variation may be a component in explaining the insignificance of income regressors (especially given that this education grouping contains fewer observations). In an effort to investigate the importance of low statistical power for our findings, a similar fixed-effects regression specification was estimated with the log of real household income as the dependent variable. This generated quite a few more statistically significant estimates—and overall goodness of fit measures around 5–7 times greater. The pooled cross-sectional results for this group (Table A2b) do not appear to offer solutions to this puzzle: instead, alongside some standard positive effects for own household income level, some additional queries are raised—by the significant negative estimate for comparison income among those under 45 years, and also the positive estimates for the magnitude of negative changes in own income.

Table 5 Individual fixed effects, high education—UK, BHPS and USoc, Waves 6–10 and 12–23

For medium and low education (Table 6), the effect of comparison income on LS is almost fully consistent with FitzRoy et al. (2014)—although only statistically significant at the 10% level (and still negative) for the younger age range. However, own income and upward changes are only positive and significant for those aged under 45. For this stratum of education, the older group sees the only substantial pre-recession decline in LS (Fig. 4). Both age groups have rising (normalised) real income, pre-recession (Figs. 8 and 9). Table 6 shows a negative effect of comparison income for the 45+ group, and that—together with the rising real income trend—could be part of the explanation for a pre-recession fall in LS. The offsetting negative externalities of economic growth, and associated social change such as increasing prevalence of non-standard and precarious employment, would instead be expected to impact especially on the younger less qualified persons.¹⁹ Corresponding pooled cross-sectional results (Table A2c) also appear similar to their counterparts for the full sample across the whole education range—albeit now with a statistically significant positive effect of comparison income on LS, for those aged under 45.

Table 6 Individual fixed effects, medium/low education—UK, BHPS and USoc, Waves 6–10 and 12–23

Given especially our struggle to explain life satisfaction for the highly educated, we consider the potential for a role of the Big Five personality traits, and especially neuroticism—as examined by Proto and Rustichini (2015), and found to ‘mediate the effect of income on life satisfaction’. The UK part of their work uses the BHPS data. However, one practical difficulty is that only BHPS Wave 15 (2005/2006) includes Big Five data—as also used in the household finances context by Brown and Taylor (2014). Proto and Rustichini (2015) argue—quite plausibly—that such traits are very stable for most people across much of their lifespan. However, fixed-effects estimation could not use raw Big Five scores taken from a single wave. Much of the analysis in Proto and Rustichini (2015) is based on the interaction between (standardised) Big Five scores and a quadratic function of income, and they also include random-effects estimation. For our investigations, the assumed zero correlation between the disturbances and the regressors, inherent in random-effects estimation, appears to be a binding (and distorting) constraint. Also, since Understanding Society Wave 3 (Wave 20 within our composite panel, for 2012–2014) also includes Big Five data—as used by Brown and Taylor (2015) to examine charitable giving behaviour—we also incorporated that information.

Although we standardise neuroticism scores prior to regression estimation, we do not undertake a preliminary regression to generate residuals as a replacement for the standardised scores, to net out certain systematic effects. This is largely because Proto and Rustichini (2015) find little difference in the results on such a basis. Our results are given in Table 7—to compare with the respective left-hand columns of Tables 4, 5 and 6. In each instance, estimates from previously listed regressors remain very similar. However, in two out of three instances, the income–neuroticism interaction’s estimates are statistically significant at the 5% level. Although it is for the highly qualified that the estimate is insignificant, its similar magnitude at least suggests the possibility that insignificance may be linked to the smaller sample size. Meanwhile, the neuroticism score estimates are significant and negative in all three columns of Table 7. Overall, it seems that the income–personality trait interaction may offer useful additional evidence, although it still appears that the picture is less clear for highly educated individuals than for others (see Online Appendix Tables A2di–A2diii for full sets of regression results). Of course, this impression is emphasised by our (well-founded) primary concentration on fixed-effects estimation—rather than pooled OLS or random effects, both of which generate greater statistical significance for more of the included regressors.²⁰ Note that our specifications including the Big Five have a systematic linkage with BHPS attrition—in the sense that any individual who left the panel prior to Wave 15 (and had not returned by Wave 23) cannot have a score for any of the Big Five personality traits.²¹

Table 7 Individual fixed effects, whole age range—UK, BHPS and USoc, Waves 6–10 and 12–23

Thus, in one sense we disagree with Easterlin (2013) by finding rising household incomes and LS for the high education group up to the recession, but we are consistent with his paradox for the less (low/medium) educated—since LS declined over this period in spite of faster rising income. Our fixed-effects estimation highlights a major puzzle—the almost complete lack of significance of any of the income variables in explaining rising LS for the high education sample. With the expansion of UK higher education reaching more families without any prior tradition, it might be that beneficiaries are simply enjoying their new-found ‘highly educated’ status independently of earnings. When the sample is not split by education, the high education dummy has its most positive (statistically significant) impact for BHPS Waves 14 and beyond (since about 2004) and for those aged 45+, who represent the traditional elite. Exploring these factors remains an important topic for future research.

4 Conclusions

Our results contradict standard findings from growth and happiness economics, but declining LS for the older least educated, in spite of growing real income until about 2010, is certainly consistent with the support of this group for populist movements in several countries, including Brexit in the UK. However, the obvious correlation between rising income and LS for the highly educated up to the crash leaves the insignificance of income variables in fixed-effects regressions for this group all the more surprising, and to the best of our knowledge, unprecedented in happiness economics. The older highly educated have the lowest LS for most of the period, right up to the recession, in spite of having the highest incomes and presumably the best jobs in the age group, and in contradiction to standard findings for other countries. We are left with major puzzles and an obvious need for more research in this area.

Appendix 1

See Figs. 10, 11 and 12.

Fig. 10

Regional gross value added per capita, deflated by CPI, 1997–2015

Fig. 11

Education categories, BHPS and USoc, aged < 45, Waves 6–23

Fig. 12

Education categories, BHPS and USoc, aged 45+, Waves 6–23