Skip to main content
SpringerLink
Log in

Health condition evaluation method for motorized spindle on the basis of optimised VMD and GMM-HMM

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

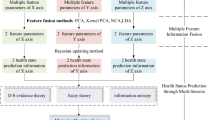
When the motorized spindles fail, the vibration signal at the bearings will contain the information related to the fault degree and operation condition. Extracting and utilising this information in an industrial environment with strong noise are the key issues of the health condition evaluation of the motorized spindles. In this paper, a health condition evaluation method for motorized spindles on the basis of optimised variational mode decomposition (VMD) and Gaussian mixture model-hidden markov model (GMM-HMM) is proposed. Firstly, using the composite index KEI as the fitness function, the parameters in the VMD are optimised by the sooty tern optimisation algorithm (STOA), and a low-dimensional feature matrix that can represent the health condition of a motorized spindle is further constructed. Secondly, the GMM-HMM of each health condition is trained, and the health condition of the motorized spindle is evaluated based on the library. Finally, the hybrid simulation signal is analysed to verify the effectiveness and superiority of the optimised VMD. The rotor unbalanced fault experiment is carried out by using the motorized spindle performance monitoring test platform. The proposed method is used to evaluate the health of the tested motorized spindle, and the results verify its superiority.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Data availability

Not applicable.

Code availability

Not applicable.

References

  1. Liu ZF, Pan MH, Zhang AP (2015) Thermal characteristic analysis of high-speed motorized spindle system based on thermal contact resistance and thermal-conduction resistance. Int J Adv Manuf Tech 76(9–12):1913–1926. https://doi.org/10.1007/s00170-014-6350-1

    Article  Google Scholar 

  2. Yang Z, Li X, Chen C (2019) Reliability assessment of the spindle systems with a competing risk model. Proc Inst Mech Eng O-J Risk Reliab 233(2):226–234. https://doi.org/10.1177/1748006X18770343

    Article  Google Scholar 

  3. Zhang Z, Cheng Q, Qi B (2021) A general approach for the machining quality evaluation of S-shaped specimen based on POS-SQP algorithm and Monte Carlo method. Manuf Syst 60:553–568. https://doi.org/10.1016/j.jmsy.2021.07.020

    Article  Google Scholar 

  4. Cheng Q, Qi B, Liu Z (2019) An accuracy degradation analysis of ball screw mechanism considering time-varying motion and loading working conditions. Mech Mach Theory 134:1–23. https://doi.org/10.1016/j.mechmachtheory.2018.12.024

    Article  Google Scholar 

  5. Moumene I, Ouelaa N (2022) Gears and bearings combined faults detection using optimized wavelet packet transform and pattern recognition neural networks. Int J Adv Manuf Tech 120(7–8):4335–4354. https://doi.org/10.1007/s00170-022-08792-2

    Article  Google Scholar 

  6. Song Y, Zeng S, Ma J (2018) A fault diagnosis method for roller bearing based on empirical wavelet transform decomposition with adaptive empirical mode segmentation. Measurement 117:266–276. https://doi.org/10.1016/j.measurement.2017.12.029

    Article  Google Scholar 

  7. Liu J, Gu Y, Chou Y (2021) Seismic data random noise reduction using a method based on improved complementary ensemble EMD and adaptive interval threshold. Explor Geophys 52(2):137–149. https://doi.org/10.1080/08123985.2020.1777849

    Article  Google Scholar 

  8. Gupta P, Singh B (2022) Ensembled local mean decomposition and genetic algorithm approach to investigate tool chatter features at higher metal removal rate. J Vib Control 28(1–2):30–44. https://doi.org/10.1177/1077546320971157

    Article  Google Scholar 

  9. Fei S-w (2017) Fault diagnosis of bearing based on wavelet packet transform-phase space reconstruction-singular value decomposition and SVM classifier. Arab J Sci Eng 42(5):1967–1975. https://doi.org/10.1007/s13369-016-2406-x

    Article  Google Scholar 

  10. Sun Y, Chen H, Shi Z (2020) A novel bevel gear fault diagnosis method based on ensemble empirical mode decomposition and support vector machines. Insight 62(1):34–41. https://doi.org/10.1784/insi.2020.62.1.34

    Article  Google Scholar 

  11. Tian Y, Ma J, Lu C (2015) Rolling bearing fault diagnosis under variable conditions using LMD-SVD and extreme learning machine. Mech Mach Theory 90:175–186. https://doi.org/10.1016/j.mechmachtheory.2015.03.014

    Article  Google Scholar 

  12. Zhu Y, Yan Q, Lu J (2020) Fault diagnosis method for disc slitting machine based on wavelet packet transform and support vector machine. Int J Comput Integr Manuf 33(10–11):1118–28. https://doi.org/10.1080/0951192X.2020.1795927

    Article  Google Scholar 

  13. Wang J, Li J, Wang H (2021) Composite fault diagnosis of gearbox based on empirical mode decomposition and improved variational mode decomposition. J Low Freq Noise Vib Act Control 40(1):332–346. https://doi.org/10.1177/1461348420908364

    Article  Google Scholar 

  14. Zhang Y, Ji J, Ma B (2020) Fault diagnosis of reciprocating compressor using a novel ensemble empirical mode decomposition-convolutional deep belief network. Measurement. https://doi.org/10.1016/j.measurement.2020.107619

    Article  Google Scholar 

  15. Dragomiretskiy K, Zosso D (2014) Variational mode decomposition. IEEE Trans Signal Process 62(3):531–544. https://doi.org/10.1109/TSP.2013.2288675

    Article  MATH  Google Scholar 

  16. Li F, Li R, Tian L (2019) Data-driven time-frequency analysis method based on variational mode decomposition and its application to gear fault diagnosis in variable working conditions. Mech Syst Signal Process 116:462–479. https://doi.org/10.1016/j.ymssp.2018.06.055

    Article  Google Scholar 

  17. An X, Zhang F (2017) Pedestal looseness fault diagnosis in a rotating machine based on variational mode decomposition. Proc Inst Mech Eng C-J Mech 231(13):2493–2502. https://doi.org/10.1177/0954406216637378

    Article  Google Scholar 

  18. Kumar A, Zhou Y, Xiang J (2021) Optimization of VMD using kernel-based mutual information for the extraction of weak features to detect bearing defects. Measurement. https://doi.org/10.1016/j.measurement.2020.108402

    Article  Google Scholar 

  19. Zhong J, Gou X, Shu Q, Liu X, Zeng Q (2021) A FOD detection approach on millimeter-wave radar sensors based on optimal VMD and SVDD. Sensors 21(3). https://doi.org/10.3390/s21030997

    Article  Google Scholar 

  20. Dhiman G, Kaur A (2019) STOA: A bio-inspired based optimization algorithm for industrial engineering problems. Eng Appl Artif Intell 82:148–174. https://doi.org/10.1016/j.engappai.2019.03.021

    Article  Google Scholar 

  21. Mor B, Garhwal S, Kumar A (2021) A systematic review of hidden markov models and their applications. Arch Comput Method Eng 28(3):1429–1448. https://doi.org/10.1007/s11831-020-09422-4

    Article  Google Scholar 

  22. Dong L, Li W-m, Wang C-H (2020) Gyro motor fault classification model based on a coupled hidden Markov model with a minimum intra-class distance algorithm. Proc Inst Mech Eng I-J Syst Control Eng 234(5):646–661. https://doi.org/10.1177/0959651819866281

    Article  Google Scholar 

  23. Cheng G, Li H, Hu X (2017) Fault diagnosis of gearbox based on local mean decomposition and discrete hidden Markov models. Proc Inst Mech Eng C-J Mech 231(14):2706–2717. https://doi.org/10.1177/0954406216638885

    Article  Google Scholar 

  24. Liu T, Chen J, Dong G (2016) Identification of bearing faults using linear discriminate analysis and continuous hidden Markov model. Proc Inst Mech Eng C-J Mech 230(10):1658–1672. https://doi.org/10.1177/0954406215582015

    Article  Google Scholar 

  25. Zheng B, Gao X (2017) Sucker rod pumping diagnosis using valve working position and parameter optimal continuous hidden Markov model. J Process Control 59:1–12. https://doi.org/10.1016/j.jprocont.2017.09.007

    Article  Google Scholar 

  26. Xia J, Shang P, Wang J (2016) Permutation and weighted-permutation entropy analysis for the complexity of nonlinear time series. Commun Nonlinear Sci 31(1–3):60–68. https://doi.org/10.1016/j.cnsns.2015.07.011

    Article  MATH  Google Scholar 

  27. Yin Y, Shang PJ (2017) Multivariate weighted multiscale permutation entropy for complex time series. Nonlinear Dynam 88(3):1707–1722. https://doi.org/10.1007/s11071-017-3340-5

    Article  Google Scholar 

  28. Tenenbaum JB, de Silva V, Langford JC (2000) A global geometric framework for nonlinear dimensionality reduction. Science 290(5500):2319-+. https://doi.org/10.1126/science.290.5500.2319

    Article  Google Scholar 

  29. Geng X, Zhan DC, Zhou ZH (2005) Supervised nonlinear dimensionality reduction for visualization and classification. IEEE Trnas Syst Man Cybern B Cybern 35(6):1098–1107. https://doi.org/10.1109/TSMCB.2005.850151

    Article  Google Scholar 

  30. Zhang M, Wan KS, Wei DD (2018) Amplitudes of characteristic frequencies for fault diagnosis of planetary gearbox. J Sound Vib 432:119–132. https://doi.org/10.1016/j.jsv.2018.06.011

    Article  Google Scholar 

  31. Zheng JD, Jiang ZW, Pan HY (2018) Sigmoid-based refined composite multiscale fuzzy entropy and t-SNE based fault diagnosis approach for rolling bearing. Measurement 129:332–342. https://doi.org/10.1016/j.measurement.2018.07.045

    Article  Google Scholar 

  32. An J, Ai P, Liu C (2021) Deep clustering bearing fault diagnosis method based on local manifold learning of an autoencoded embedding. IEEE Access 9:30154–30168. https://doi.org/10.1109/ACCESS.2021.3059459

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by Jilin Science and Technology Development Plan-Key R&D Program (20210201055GX).

Author information

Author notes

  1. Guofa Li

    Present address: Key Laboratory of CNC Equipment Reliability, Ministry of Education, Jilin University, Changchun, 130025, China

Authors and Affiliations

  1. Key Laboratory of CNC Equipment Reliability, Ministry of Education, Jilin University, Changchun, 130025, China

    Haiji Yang, Jialong He & Liding Wang

  2. School of Mechanical and Aerospace Engineering, Jilin University, Changchun, 130025, China

    Haiji Yang, Guofa Li, Jialong He & Liding Wang

  3. Faw Jiefang Automot CO., LTD, Changchun, 130025, China

    Xinyu Nie

Authors
  1. Haiji Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Guofa Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jialong He
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Liding Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xinyu Nie
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Haiji Yang: Background research, Data curation, Software, Validation writing-original draft, Editing. Guofa Li: Methodology, Review & editing, Supervision. Jialong He: Project administration, Funding acquisition. Liding Wang: Supervision. Xinyu Nie: Assist in experiment. All authors read and approved the final manuscript.

Corresponding authors

Correspondence to Guofa Li or Jialong He.

Ethics declarations

Ethics approval

Not applicable.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Conflict of interest

The authors declare no competing interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, H., Li, G., He, J. et al. Health condition evaluation method for motorized spindle on the basis of optimised VMD and GMM-HMM. Int J Adv Manuf Technol 124, 4465–4477 (2023). https://doi.org/10.1007/s00170-022-10202-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-022-10202-6

Keywords

Search

Navigation