Skip to main content
SpringerLink
Log in

High efficiency and precision approach to milling stability prediction based on predictor-corrector linear multi-step method

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

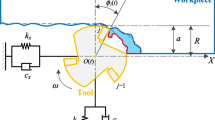
Regenerative chatter is the most important factor affecting the stability of the milling process. It is core for suppressing chatter and improving production efficiency to accurately and efficiently identify the stable region of milling chatter. Therefore, according to the theory of predictor-corrector, three predictor–corrector methods (PCM) are, respectively, proposed for the milling stability region by applying the fourth-order Adams-Bashforth-Moulton formula, Simpson formula, and Hamming formula. Firstly, the regenerative chatter milling process is described as a second-order time-delay differential equation (DDE) with periodic coefficients. Thus, the forced vibration time can uniformly be discretized as a time node set. Secondly, the fourth-order Adams-Bashforth formula is used to predict the displacement at every time node, whereas the fourth-order Adams-Moulton formula can be employed to correct this predicted value. In addition, the fourth-order Simpson formula and Hamming formula can also correct the predicted value. Thus, a higher precision discrete prediction-correction expansion is constructed for the transformation of DDE into the state transition express. The Floquet theory can be depended on to present the judgment criterion of milling stability. Moreover, finally, under the same milling process parameters, comparisons of both the stability lobe curve and the local discrete error curve show that the PCM has a faster convergence rate than the 1st-SDM (first-order semi-discretization method) and 2nd-FDM (second-order full-discretization method). This shows that the PCM can obtain better computational accuracy under the same discrete number, whereas the PCM is significantly higher computational efficiency over 1st-SDM and 2nd-FDM. Meanwhile, considering the actual machining environment, helix angle effect and multiple modes effect of the tool are analyzed; experimental verification considering multiple modes with helix angle further indicates the applicability of the PCM.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Availability of data and material

All included in the paper.

Code availability

Not applicable.

References

  1. Altintas Y, Weck M (2004) Chatter stability of metal cutting and grinding. CIRP Ann Manuf Technol 53(2):619–642

    Article  Google Scholar 

  2. Altintas Y (2012) Manufacturing automation: metal cutting mechanics, machine tool vibrations, and CNC design. Cambridge University Press, Cambridge

    Book  Google Scholar 

  3. Faassen RPH, Van de WN, Oosterling JAJ, Nijmeijer H (2003) Prediction of regenerative chatter by modelling and analysis of high-speed milling. Int J Mach Tools Manuf 43(14):1437–1446

    Article  Google Scholar 

  4. Altintas Y, Stepan G, Merdol D, Dombovari Z (2008) Chatter stability of milling in frequency and discrete time domain. CIRP J Manuf Sci Technol 1(1):35–44

    Article  Google Scholar 

  5. Balachandran B (2001) Nonlinear dynamics of milling processes. Philos Trans R Soc A 359(1781):793–819

    Article  MATH  Google Scholar 

  6. Wiercigroch M, Budak E (2001) Sources of nonlinearities, chatter generation and suppression in metal cutting. Philos Trans R Soc A 359(1781):663–693

    Article  MATH  Google Scholar 

  7. Li H, Shin YC (2006) A comprehensive dynamic end milling simulation model. Trans ASME J Manuf Sci Eng 128(1):86–95

    Article  Google Scholar 

  8. Minis I, Yanushevsky R (1993) A new theoretical approach for the prediction of machine tool chatter in milling. Trans ASME J Manuf Sci Eng 115(1):1–8

    Article  Google Scholar 

  9. Campomanes ML, Altintas Y (2003) An improved time domain simulation for dynamic milling at small radial immersions. Trans ASME J Manuf Sci Eng 125(3):416–422

    Article  Google Scholar 

  10. Davies MA, Pratt JR, Dutterer BS (2000) The stability of low radial immersion milling. CIRP Ann Manuf Technol 49(1):37–40

    Article  Google Scholar 

  11. Davies MA, Pratt JR, Dutterer BS (2002) Stability prediction for low radial immersion milling. Trans ASME J Manuf Sci Eng 124(2):217–225

    Article  Google Scholar 

  12. Altintas Y, Budak E (1995) Analytical prediction of stability lobes in milling. CIRP Ann Manuf Technol 44(1):357–362

    Article  Google Scholar 

  13. Merdol S, Altintas Y (2004) Multi-frequency solution of chatter stability for low immersion milling. Trans ASME J Manuf Sci Eng 126(3):459–466

    Article  Google Scholar 

  14. Altintas Y, Lee P (1998) Mechanics and dynamics of ball end milling. Trans ASME J Manuf Sci Eng 120(4):684–692

    Article  Google Scholar 

  15. Altintas Y, Engin S, Budak E (1999) Analytical stability prediction and design of variable pitch cutters. Trans ASME J Manuf Sci Eng 121(2):173–178

    Article  Google Scholar 

  16. Altintas Y (2001) Analytical prediction of three dimensional chatter stability in milling. JSME Int J Ser C 44(3):717–723

    Article  MathSciNet  Google Scholar 

  17. Turner S, Merdol D, Altintas Y, Ridgway K (2007) Modelling of the stability of variable helix end mills. Int J Mach Tools Manuf 47(9):1410–1416

    Article  Google Scholar 

  18. Ko JH, Altintas Y (2007) Dynamics and stability of plunge milling operations. Trans ASME J Manuf Sci Eng 129(1):32–40

    Article  Google Scholar 

  19. Bayly PV, Halley JE, Mann BP, Davies MA (2003) Stability of interrupted cutting by temporal finite element analysis. Trans ASME J Manuf Sci Eng 125:220–225

    Article  Google Scholar 

  20. Insperger T, Stepan G (2002) Semi-discretization method for delayed systems. Int J Numer Methods Eng 55(5):503–518

    Article  MathSciNet  MATH  Google Scholar 

  21. Insperger T, Stepan G (2004) Updated semi-discretization method for periodic delay-differential equations with discrete delay. Int J Numer Methods Eng 61:117–141

    Article  MathSciNet  MATH  Google Scholar 

  22. Insperger T, Stepan G, Turi J (2008) On the higher-order semi-discretizations for periodic delayed systems. J Sound Vib 313(1):334–341

    Article  Google Scholar 

  23. Ding Y, Zhu LM, Zhang XJ, Ding H (2010) A full-discretization method for prediction of milling stability. Int J Mach Tools Manuf 50(5):502–509

    Article  Google Scholar 

  24. Ding Y, Zhu LM, Zhang XJ, Ding H (2010) Second-order full-discretization method for milling stability prediction. Int J Mach Tools Manuf 50(10):926–932

    Article  Google Scholar 

  25. Wan M, Zhang WH, Dang JW, Yang Y (2010) A unified stability prediction method for milling process with multiple delays. Int J Mach Tools Manuf 50(1):29–41

    Article  Google Scholar 

  26. Quo Q, Sun YW, Jiang Y (2012) On the accurate calculation of milling stability limits using third-order full-discretization method. Int J Mach Tools Manuf 62(1):61–66

    Article  Google Scholar 

  27. Liu YL, Zhang DH, Wu BH (2012) An efficient full-discretization method for prediction of milling stability. Int J Mach Tools Manuf 63:44–48

    Article  Google Scholar 

  28. Sun YX, Xiong ZH (2017) High-order full-discretization method using Lagrange interpolation for stability analysis of turning processes with stiffness variation. J Sound Vib 386:50–64

    Article  Google Scholar 

  29. Ozoegwu CG, Omenyi SN (2016) Third-order least squares modelling of milling state term for improved computation of stability boundaries. Prod Manuf Res 4(1):46–64

    Google Scholar 

  30. Ozoegwu CG, Omenyi SN, Ofochebe SM (2015) Hyper-third order full-discretization methods in milling stability prediction. Int J Mach Tools Manuf 92:1–9

    Article  Google Scholar 

  31. Tang XW, Peng FY, Yan R, Gong YH, Li YT, Jiang LL (2017) Accurate and efficient prediction of milling stability with updated full-discretization method. Int J Adv Manuf Technol 88(9–12):2357–2368

    Article  Google Scholar 

  32. Tang XW, Peng FY, Yan R, Gong YH, Li X (2016) An effective time domain model for milling stability prediction simultaneously considering multiple modes and cross-frequency response function effect. Int J Adv Manuf Technol 86(1):1037–1054

    Article  Google Scholar 

  33. Zhou K, Zhang JF, Xu C, Feng PF, Wu ZJ (2018) Effects of helix angle and multi-mode on the milling stability prediction using full-discretization method. Precis Eng 54:39–50

    Article  Google Scholar 

  34. Zhang XJ, Xiong CH, Ding Y, Ding H (2017) Prediction of chatter stability in high speed milling using the numerical differentiation method. Int J Adv Manuf Technol 89(9):2535–2544

    Article  Google Scholar 

  35. Li MZ, Zhang GJ, Huang Y (2013) Complete discretization scheme for milling stability prediction. Nonlinear Dyn 71(1–2):187–199

    Article  MathSciNet  Google Scholar 

  36. Ding Y, Zhu LM, Zhang XJ, Ding H (2011) Numerical integration method for prediction of milling stability. Trans ASME J Manuf Sci Eng 133(3):031005

    Article  Google Scholar 

  37. Niu JB, Ding Y, Zhu LM, Ding H (2014) Runge-Kutta methods for a semi-analytical prediction of milling stability. Nonlinear Dyn 76(1):289–304

    Article  MathSciNet  MATH  Google Scholar 

  38. Olvera D, Elías-Zúñiga A, Martínez-Alfaro H, De Lacallec LL, Rodrígueza CA, Campa FJ (2017) Determination of the stability lobes in milling operations based on homotopy and simulated annealing techniques. Mechatronics 24(3):177–185

    Article  Google Scholar 

  39. Zhang Z, Li HG, Meng G (2015) A novel approach for the prediction of the milling stability based on the Simpson method. Int J Mach Tools Manuf 99:43–47

    Article  Google Scholar 

  40. Qin CJ, Tao JF, Liu CL (2019) A novel stability prediction method for milling operations using the holistic-interpolation scheme. Proc IME C J Mech Eng Sci 233(13):4463–4475

    Article  Google Scholar 

  41. Dai YB, Li HK, Xing X, Hao B (2018) Prediction of chatter stability for milling process using precise integration method. Precis Eng 52:152–157

    Article  Google Scholar 

  42. Dong XF, Qiu ZZ (2020) Stability analysis in milling process based on updated numerical integration method. Mech Syst Signal Process 137:106435

    Article  Google Scholar 

  43. Lou WD, Qin GH, Zuo DW (2021) Investigation on Cotes-formula-based prediction method and its experimental verification of milling stability. J Manuf Process 64:1077–1088

    Article  Google Scholar 

  44. Wu Y, You YP, Jiang JJ (2020) New predictor-corrector methods based on piecewise polynomial interpolation for milling stability prediction. Mach Sci Technol 24(5):688–718

    Article  Google Scholar 

  45. Stoer J, Bulirsch R (2013) Introduction to numerical analysis. Springer Science & Business Media, London

    MATH  Google Scholar 

  46. Mann BP, Young KA, Schmitz TL, Dilley DN (2005) Simultaneous stability and surface location error predictions in milling. Trans ASME J Manuf Sci Eng 127(3):446–453

    Article  Google Scholar 

  47. Bayly PV, Mann BP, Schmitz TL, Peters DA, Stepan G (2002) Insperger T (2002) Effects of radial immersion and cutting direction on chatter instability in end-milling. ASME IMECE 3641:351–363

    Google Scholar 

  48. Zatarain M, Munoa J, Peigne G, Insperger T (2006) Analysis of the influence of mill helix angle on chatter stability. CIRP Ann 55(1):365–368

    Article  Google Scholar 

  49. Mann BP, Edes BT, Easley SJ, Young KA, Ma K (2008) Chatter vibration and surface location error prediction for helical end mills. Int J Mach Tools Manuf 48(3–4):350–361

    Article  Google Scholar 

Download references

Funding

This work is supported by the National Nature Science Foundation of China (Grant No. 51765047), the Major Discipline Academic and Technical Leader Training Plan Project of Jiangxi Province (Grant No. 20172BCB22013), and the Key Research and Development Plan Project of Jiangxi Provincial Science and Technology Department (Grant No. 20203BBE53049).

Author information

Authors and Affiliations

  1. School of Aeronautical Manufacturing Engineering, Nanchang Hangkong University, Nanchang, 330063, China

    Guohua Qin, Huamin Wang & Zhuxi Wu

  2. School of Mechanical Engineering, Northwestern Polytechnical University, Xi’an, 710072, China

    Guohua Qin & Weida Lou

Authors
  1. Guohua Qin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Weida Lou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Huamin Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zhuxi Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Guohua Qin: conceptualization, methodology, investigation, writing—review and editing. Weida Lou: conceptualization, methodology, formal analysis, writing—original draft. Huamin Wang: writing, review; data curation. Zhuxi Wu: language modification, data analysis.

Corresponding author

Correspondence to Guohua Qin.

Ethics declarations

Ethics approval

Our research does not involve humans and animals, so there is no need to provide ethical approval.

Consent to participate and publish

All authors agreed to participate and publish.

Competing interests

The authors declare no competing interests.

Additional information

Publisher's note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Qin, G., Lou, W., Wang, H. et al. High efficiency and precision approach to milling stability prediction based on predictor-corrector linear multi-step method. Int J Adv Manuf Technol 122, 1933–1955 (2022). https://doi.org/10.1007/s00170-022-09952-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-022-09952-0

Keywords

Search

Navigation