1 Introduction

Metal parts can be traditionally fabricated by additive manufacturing (AM) processes such as Laser Powder bed fusion (LPBF), direct energy deposition (DED) and electron beam melting (EBM) [1]. These conventional metal additive manufacturing (metal AM) technologies have been studied and developed for academic and industrial applications such as biomedical field, aerospace and military. However, laser-beam technologies are generally high-energy consuming and expensive, since they demand high energy to melt the metallic powders, operate in inert gas environments and require cooling systems; hence, they have high installation and maintenance costs. Therefore, alternative low-cost metal AM techniques are desired. As an alternative, metal-fused filament fabrication (metal FFF) was proposed for the realization of metal parts at low energy consumption and low cost. The idea of using FFF or fused deposition modelling (FDM) for the manufacturing of metal parts was first presented by Wu et al. [2] with stainless steel 17–4 PH. This process was later on referred to as metal FFF or FDMet [2, 3]. Manufacturers realized a composite material made by the combination of metal powder and a thermoplastic binder, which can be extruded by a traditional FFF printer. Subsequently, debinding and sintering process steps are conducted on the printed parts to form compact full metal parts. The first 3D printed part is defined as “green part”, thus a debinding and, finally, a sintering process are necessary to obtain, respectively, the “brown part” and the “white part”. The entire process chain is called “shaping, debinding and sintering-SDS-process”. During the first step, called “shaping”, the metal-polymer composite in the form of filament is extruded at a temperature sufficient to melt the binder and leave the metal particles solid. Subsequently, during the “debinding”, brown parts are obtained after the removal of most of the polymer binder, which can occur through different methodologies. The remaining polymer binder in the brown parts avoids the spreading of the metal particles and thus preserves the shape of the parts, which has to be subjected to the last, “sintering” phase. The latter, which takes place in a furnace, allows to obtain full metal parts, by melting the metal particles together and eliminating the remaining polymer [4].

Very few years ago, Markforged Inc. Company launched a new patented technology called atomic diffusion additive manufacturing (ADAM), characterized by a very similar process chain, which involves, as first step, the 3D printing of a filament made by metal powder bound in a plastic matrix. In particular, the Metal X series machines comprises a first 3D printer machine, a debinding washer and a sintering furnace. The material adopted by Markforged are 17–4 PH Stainless Steel (launch material), and other materials, such as Tool Steels (H13, A2, D2), Inconel 625 and copper [5]. Almost contemporary, another commercial solution was proposed by Desktop Metal Inc., which uses a different 3D printing technology based on plunger-based extrusion process. This technology named Bound Metal Deposition™ does not use a spool of filament, but cartridge containing bars of metal-polymer composite. Both Markforged and Desktop Metal use proprietary materials, machines and software; thus, the possibility of using a filament with similar composition printable by already existing and low-cost machines is a great advantage.

The material portfolio for Metal FFF on consumer 3D printers is still limited to few materials: 316L [1, 3, 6,7,8,9] and 17–4 PH [2, 10,11,12] stainless steels, titanium alloys [9, 13] and pure copper [14, 15]. These filaments are typically made in laboratories and used by research centres. As commercial solutions, the one offered by BASF 3D Printing Solutions GmbH group company is probably the best known, thanks to the possibility to provide spools of filaments ready to be printed on existing and cost-effective 3D printers, usually used for processing polymers, with extruders able to reach temperature of maximum 240–260 °C. The interest towards these filaments is rapidly increasing, and great attention is dedicated to the potentiality of this novel AM technique. However, being a process composed by different phases, it is characterized by many issues derived from the shaping, debinding and sintering phases which affect the quality and performances of the final part. In this context, the 3D printing by using FFF techniques has some typical defects, such as dimensional inaccuracies, possible delamination, high surface roughness, high porosity, warping and anisotropic mechanical behaviour. These aspects limit the applications of this technology to the fabrication of functional prototypes and tools with lower costs of energy and material. While, concerning the manufacturing of structural parts for crucial sectors like the biomedical and aerospace ones, this technology is still considered unsuitable. The study of the mechanical performances of the final part in relation to different process parameters, becomes, then, of paramount importance.

2 State of the art

Materials suitable for consumer 3D printer are relatively recent. Thus, in literature, to the authors’ knowledge, still few works are reported, mainly focused on traditional mechanical characterization, porosity and shrinkage analysis. Liu et al. [1] provided, in addition to the mechanical behaviour analysis, an investigation on the obtained microstructure in terms of density and shrinkage. Gong et al. [7, 16] conducted a study for the evaluation of the mechanical properties of Ultrafuse 316L through tensile test using conventional strain gauge and hardness test, comparing the results obtained with the same specimens made by selective laser melting (SLM). Also, the shrinkage phenomenon after the debinding and sintering (D&S) was evaluated. A further comparison between the 316L FFF parts and the 316L parts made by SLM was provided by Schumacher and Moritzer [17], using a raster strategy and variable filling geometry. In both cases, the SLM specimens showed the highest values of yield strength and ultimate tensile strength but lower ductility. Tosto et al. [18] realized Ultrafuse 316L tensile specimens according to the ASTM D638 with flatwise and upright orientation for evaluating the mechanical properties. Ait-Mansour et al. [19] studied the Ultrafuse 316L with tensile and compression tests with different theoretical infill (25% to 125%) and different build orientation (flatwise, sideways and upright). Damon et al. [20] evaluated the porosity through the ultrasonic method and related it with the typical mechanical properties of the build strategies. Quarto et al. [21] focused on the shrinkage and density evaluation analysing the main 3D printing parameters for obtaining a full dense metal part. Carminati et al. [22] highlighted the ultimate/yield strength and elongation at break of Ultrafuse 316L parts through tensile, flexural, compressive and impact test and defined the effect of sintering phase on the microstructure.

As reported, the state of the art relating to the study of mechanical properties of the investigated material by means of tensile tests [6, 16, 22, 23] comprises the use of conventional methods (strain gauges and extensometer), and the main extracted parameters are Young’s modulus, elongation at break and ultimate/yield strength. Although, these conventional methods can give, in some cases, incomplete information about the strain behaviour, the failure progression before breaking and the evaluation of Poisson’s ratio, which is essential for fully characterising the mechanical performance of materials. This knowledge is of great importance to understand the influence of 3D printing parameters and deposition strategies on mechanical properties of FFF parts for the results calculation under static and variable loads by means of analytical and numerical methods. The typical filament scale structure, indeed, produces a non-uniform distribution of strain. A technology able to evaluate the strain localization and track the failure progression is the digital image correlation (DIC). DIC is an image-based optical method for full-field measurement of shape, displacement and deformation. This method works according to the correlation principle by comparing digital photographs of a component (or test piece) at different stages of deformation. Therefore, there is a reference image which is considered the initial state of the specimen (undeformed state). Then, the quantities such as deformation and displacement are determined by comparing the subsequent images. By tracking blocks of pixels, the system can measure surface displacement and build up full field 2D and 3D deformation vector fields and strain [24, 25]. Some applications of DIC for FFF of polymers are reported in previous works [26,27,28,29]. In the field of metal FFF technologies, the DIC can be implemented to study the effect of parameters such as building orientation, number of wall layers, infill density, etc. on the mechanical properties of the 3D-printed parts. Moreover, the full-field DIC maps of strains can show the anisotropy of parts during the mechanical tests and allow to evaluate the Poisson’s ratio punctually. DIC applied for the mechanical characterization of metal FFF would allow to better understand the mechanical behaviour of the parts when varying some fundamental process parameters and make the study of the printed parts performance more reliable. An application of DIC on metal FFF is reported by Henry et al. [30], where tensile, shear and bending tests were conducted on 17–4 PH stainless steel specimens realized by the ADAM technology to evaluate the mechanical properties of material.

In this paper, DIC was applied during the execution of tensile tests on 316L stainless steel specimens produced with a layerwise technology, in order to analyse the mechanical properties (ultimate tensile strength, yield strength, Young’s modulus, elongation at break, Poisson’s ratio) for three different building orientations and number of wall layers. The use of the DIC technique allowed, in addition, to locally monitor the strain evolution along the gauge length and in correspondence of break section of specimens, to evaluate the effect of anisotropy on properties, enabling a complete characterization of material useful for finite element analysis and numerical methods.

3 Materials and methods

3.1 Material: BASF 316L filament

The material considered in this study is the BASF Ultrafuse® 316L (BASF 3D Printing Solutions GmbH, Germany), a metal-polymer composite, composed of about 88% of 316L stainless steel [31] in the form of powder with a various particle sizes (Fig. 1) from 2 to 17 μm and a thermoplastic matrix which acts as a binder. The chemical composition of the filament was evaluated through the EDS analysis and reported in Table 1. The polymeric part is divided in a main binder, a backbone binder and other additives. The polyoxymethylene (POM) is the main binder, which triggered the phenomenon of catalysis in the debinding phase, thanks to its chemical structure. The Ultrafuse®, indeed, is the equivalent of Catamold® in the process of metal injection moulding; both are totally unique in their ability for catalytic gas phase decomposition of the binder. The backbone binder is polypropylene (PP), and there are also additives like dioctyl phthalate (DOP), dibutyl phthalate (DBP) and zinc oxide (ZnO) to increase the fluidity, plasticity and thermostability of the composite, as reported by Liu et al. [1]. The declared density of filament is 5.00 g/cm3 for a spool of material with diameter of 1.75 ± 0.075 mm [32]. This statement was nearly confirmed by a basic experimental evaluation on 1 m of filament, whose weight and diameter were measured, respectively, with a precision balance and with a micrometre. In this case, the average diameter was 1.77 ± 0.025 mm and the relative density, 4.85 g/cm3.

Fig. 1
figure 1

SEM image of BASF Ultrafuse 316L filament: some powder particles of 316L stainless steel are indicated with white arrows

Full size image
Table 1 Chemical composition of BASF Ultrafuse 316L filament after EDS analysis
Full size table

3.2 Experimental set-up and experimental plan

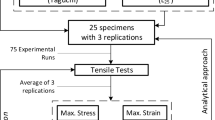
The main objective of this study was to investigate the influence of some printing conditions, i.e. the building orientations and the number of wall layers, on the mechanical properties of metal FFF–printed specimens using a consolidated method as DIC. The methodology followed in this study is outlined in Fig. 2.

Fig. 2
figure 2

Workflow of activities

Full size image

Dimensions and shape of tensile test specimens were referred to standard UNI EN ISO 6892–1 [33]. However, due to the loss of material during the debinding and sintering phases, nominal dimensions were properly oversized. According to the guidelines of BASF and a sintering on XY plan, a scale multiplier of 1.19 for length and width and 1.25 for thickness was chosen. Ultimaker Cura® was used for the orientation of the specimen on the building plate, for setting the main printing parameters and for the specimen slicing. The printing machine used in this work was a Creatbot F430 (Henan Creatbot Technology Limited, China) with two extruders and a heated plate and heated chamber. A ruby nozzle with 0.4 mm of diameter was used for the shaping of the specimens.

The main printing parameters used for the fabrication of all the samples were selected after preliminary tests. They are reported in Table 2.

Table 2 Printing parameters
Full size table

With these parameters, nine different groups of specimens were printed, according to factors and levels reported in Table 3, varying two variables, i.e. the build orientation (Fig. 3) and the number of wall layers with 3 replications for each. By considering three building orientations, it was possible to analyse the effects of anisotropy typical of layerwise technologies as explored by Pereira et al. [34] and Pérez-Ruiz et al. [35, 36] during machining operations on parts realized via metal AM techniques, by Jiang and Ning [37] on the shrinkage behaviour during SDS and by Gabilondo et al. [38] on mechanical behaviour.

Table 3 Experimental plan with two factors and three levels for each
Full size table
Fig. 3
figure 3

Different strategies used for the shaping of different specimens

Full size image

During the printing phase, to avoid the onset of warpage during the deposition of the first layers of the specimens and to improve the adhesion to the building plate, 20 lines of brim and the Dimafix® glue spray were used, and, only for the flatwise specimens, in addition to these, Kapton tape was also used for obtaining a warpage-free printing result. The D&S phases were conducted according to the BASF 3D Printing Solutions GmbH guidelines [31] at an external service. For the catalytic debinding, a temperature of 120 °C with a holding time of 8 h and over the 98% of nitric acid was used to preliminarily remove the polymeric matrix. The subsequent sintering phase was divided in two steps. In the first one, specimens were overheated up to 600 °C for 1 h to burn the remaining binder, while, in the second step, specimens were kept for 3 h at a temperature of 1380 °C, and, subsequently, cooled. During the D&S, the specimens were positioned in the same flatwise orientation to avoid the collapse of the part on itself due to the peculiar geometry of the tensile test specimens characterized by a small thickness and a high height-to-width ratio. BASF in its guidelines, indeed, suggests to debound and sinter parts with height-to-width ratio higher than 3:1 in a flatwise position, regardless of the build orientation of the part during the shaping.

Before the tensile tests, density [21] (ρ) was evaluated for both green and sintered parts. In particular, it was evaluated, as the ratio between weight (g) and volume (cm3) of each specimen (cfr. (1) and (2)). The weight was estimated using a precision balance, while the volume using the dimensions was measured with a precision calliper. Measurements were repeated three times, and the average values were considered in the computation:

$${\mathrm{Density }\left(\rho \right)}_{\mathrm{green}} (\mathrm{g}/{\mathrm{cm}}^{3})=\frac{{\mathrm{Weight}}_{\mathrm{green}}}{{\mathrm{Volume}}_{\mathrm{green}}}$$
(1)
$${\mathrm{Density }(\rho )}_{\mathrm{sintered}} (\mathrm{g}/{\mathrm{cm}}^{3})= \frac{{\mathrm{Weight}}_{\mathrm{sintered}}}{{\mathrm{Volume}}_{\mathrm{sintered}}}$$
(2)

This analysis was carried out for allowing a more complete discussion of the mechanical test results reported in the next sections.

3.3 Tensile tests and DIC system

On the fabricated specimens, uniaxial tensile tests at room temperature were performed by means of a universal testing machine with a load cell of 200 kN assisted by the DIC system ARAMIS 3D provided by GOM (Gesellschaft für Optische Messtechnik GmbH, Germany) to continuously acquire the strain distribution during the test. This DIC system was equipped with two cameras characterized by 12 Megapixel (4096 × 3000 pixel) of sensor’s resolution, 24-mm objective lenses and a led illuminator. Cameras were placed facing the gauge length of specimen. Before tests, a calibration procedure with a dedicated panel was conducted. During calibration phase, it is imposed a constant illumination, the value of measuring volume, the working distance between specimen and cameras (≃ 687 mm) and the slider distance between the two adopted cameras (266 mm). The entire process of panel positioning is guided, ensuring highly accurate calibration results. However, after the calibration phase, the user is provided with the calibration accuracy value. In this way, the user can decide whether to repeat the calibration or continue with the test. Thus, this DIC system was implemented during the tensile test execution. Before the tensile test, the specimens were prepared with a high-contrast black-on-white speckle pattern. The specimens were first stained with a white matte layer background to avoid reflection and then sprayed with a random black speckle pattern. Once the test has started, after reaching 2% of strain, the speed was gradually increased up to 10 mm/min, and this value kept constant until the breaking of the specimen.

Data collected during the tensile tests by the DIC equipment was subsequently analysed by using the GOM Aramis software. The yield strength (YS), the ultimate tensile strength (UTS), Young’s modulus (E), the elongation at break (A) and the Poisson’s ratio (ν) were evaluated. The elongation at break was evaluated in the break section considering the maximum value of Von Mises equivalent strain (technical strain) (3), while the Poisson’s ratio through the well-known Eq. (4). For the latter, on each specimen, two columns of point distributed every 4 mm and placed on the gauge length were considered for the computation of the εx and εy. The values of εx and εy were defined in the elastic field:

$${Von \;Mises \;Equivalent \;strain}: \varepsilon = \sqrt{\frac{2}{3}*({\varepsilon }_{1}^{2}+{\varepsilon }_{2}^{2}+{\varepsilon }_{3 }^{2})}$$
(3)
$$\textit{Poisson's ratio}\mathit:\;\nu\;\mathit{\left(\text{elastic field}\right)}=-\frac{\varepsilon_x(elastic\;field)}{\varepsilon_y(elastic\;field)}$$
(4)

4 Results and discussion

4.1 Density analysis

As first analysis, the density of green and sintered specimens was evaluated, according to Eqs. (1) and (2).

In Fig. 4, the trend of both densities is reported.

Fig. 4
figure 4

Plot of the green and sintered densities evaluated for each specimen. The specimen number refers to the number of test specimen coming from the randomise order of the experimental plan

Full size image

The densities of the corresponding green/sintered specimens showed a similar trend, and some more representative cases characterized by a good correlation between green and sintered densities are indicated with red circles. Considering the sintered specimens, grouped by the building orientation, the density was evaluated according to the number of wall layers (Fig. 5a–c). The specimens were identified with different letters according to the building orientation: upright as “U”, sideways as “S” and flatwise as “F”. The number of wall layers, instead, was expressed with the Arabic number 2, 4 and 6.

Fig. 5
figure 5

Trend of sintered density varying number of wall layers: a for upright specimens, b for sideways specimens, c for flatwise specimens. The specimens marked with a black circle and Roman number were further analysed at optical microscope for a porosity evaluation

Full size image

Figure 5a–c show the ρsintered values. In Fig. 5a, the upright with 4 wall layers reported the lowest values of density with a minimum of 6.45 g/cm3. For the other two configurations (2 and 6 wall layers), the values were slightly higher but variable in the same group of specimens. In Fig. 5b, the sideways specimens with 2 wall layers reported a great variability (6.70–7.31 g/cm3), while the other two configurations were characterized by lower and less variable values. The flatwise specimens (Fig. 5c) showed similar densities for the 2 and 4 wall layers (≃ 7.10 g/cm3), while there was a decrease in the 6 wall layer specimens. In general, considering all configurations, the building orientation and number of wall layers affected the sintered density.

For a more detailed analysis and to obtain an insight of the voids distribution in the produced parts, some cross sections of the specimens marked by a black circle and a Roman number in Fig. 5a–c were observed with an optical microscope (magnification of 140x). In particular, cross-sections parallel to the building orientation (Fig. 6) were considered.

Fig. 6
figure 6

Cross-section of specimens parallel to the building direction: I upright-2, II upright-4, III sideways-2 IV sideways-6, V flatwise-4, VI flatwise-6

Full size image

Using the ImageJ software (https://imagej.nih.gov/ij/), an image analysis on these cross-sections was carried out after the binarization of the images for the evaluation of porosity. The voids distribution was mostly concentrated in correspondence of the layer-layer adhesion, wall layer-wall layer adhesion and wall layer-infill pattern adhesion. Porosity as percentage value of the ratio between black area (voids) and total area was then evaluated. For the upright specimens, this value was 1.80% for the 2 wall layers and 4.52% for 4 wall layers. The sideways specimen with 2 wall layers registered 1.74% of porosity, while the sideways specimen with 6 wall layers 4.05%. Comparing a flatwise specimen with 4 wall layers and a flatwise specimen with 6 wall layers, the porosity varied between 2.89 and 5.30%.

These two evaluations, density and porosity by micrographs, were both used for the discussion about the mechanical properties estimated in the next sections.

4.2 Tensile test results

The stress–strain curves obtained during the tensile tests allowed to highlight the mechanical properties of the BASF Ultrafuse 316L specimens. By plotting the values of UTS, YS, E and A as a function of the number of wall layers and the building orientation, the graphs in Fig. 7a–d were obtained. The values of UTS, YS, E and A shown in the graphs were obtained by averaging the values derived from three replications. The reported figures show also the standard deviations of the obtained values in the form of error bars.

Fig. 7
figure 7

a UTS values as a function of the number of wall layer and printing orientation. b YS values as a function of the number of wall layer and printing orientation. c E values as a function of the number of wall layer and printing orientation. d A values as a function of the number of wall layer and printing orientation

Full size image

Looking first at the values obtained for the UTS, it is possible to observe that the sideways specimens registered UTS values greater than the other two building orientations. This is related to the parallel orientation of the layers with respect to the tensile load direction (Fig. 8a). On the contrary, the specimens with the upright orientation showed the lowest UTS except for the six wall layers configuration. This is justified by the orthogonal layers’ orientation with respect to the applied load direction (Fig. 8b). Flatwise specimens showed UTS values comparable with the ones obtained for the sideways specimens with the lowest standard deviations. More in details, the obtained values were comprised between 401 and 439.3 MPa, for the sideways; between 387.7 and 405.2 MPa for the flatwise and, finally, between 345 and 399.6 MPa for the upright.

Fig. 8
figure 8

Scheme of applied force on specimens with different orientations. a Sideways orientation. b Upright orientation

Full size image

Considering the yield strength (Fig. 8b) behaviour, with respect to the different orientations, the sideways specimens were characterized by the highest values (range between 127.5 and 132.7 MPa), while the flatwise and upright by slightly lower values: 106.7 to 125.7 MPa and 117 to 122.7 MPa, respectively. The results obtained for UTS and YS, at different combinations of parameters, are lower if compared to a 316L standard [39] (485 MPa and 170 MPa respectively). These differences compared to a 316L flat rolled show a significant anisotropy for 316L AM parts.

Regarding the Young’s modulus (Fig. 7c), E, was found to be higher for upright specimens (range from 176.37 to 188.94 GPa) compared to sideways (range from 142.42 to 185.64 GPa) and flatwise (range from 143.91 to 182.83 GPa) specimens, but lower if compared to 193 GPa of the standard material. For the same reason, the upright specimens were characterized by the lowest elongation at break (A) compared to the flatwise and sideways specimens (Fig. 7d). This value was comprised between 25 and 35% for the upright, 38 and 45% for the flatwise and 33 and 43% for the sideways. The elongation at break of flatwise and sideways specimens was consistent with the standard [39] (40%) with respect to sideways and upright specimens. Moreover, the error bars showed a lower variability of results for the UTS, YS, while higher variability was registered for A and for the E values.

As expected, upright specimens showed the lowest values of UTS and YS. However, there was an exception if six wall layers are considered. In this case, flatwise specimens were characterized by the lowest mechanical characteristics in terms of UTS and YS, lower than the upright. The reason of this behaviour could be related to a delamination defect arouse during the sintering, as a lack of adhesion between wall layers and between the infill pattern and wall layers (Fig. 9). This defect started during the shaping phase, and it was worsened during the D&S phases, due to the shrinkage phenomenon, negatively affecting the sintered parts in terms of dimensions and mechanical properties, by reducing the load-bearing section. Moreover, considering the value of density and the porosity estimated through the micrographs, for the flatwise reported in Fig. 5c, the lowest values of the F-6 specimens compared to F-2 and F-4 and the highest porosity can justify the worsening of mechanical properties together to the delamination defect.

Fig. 9
figure 9

Defects of delamination on green and sintered parts of a six-wall flatwise specimen

Full size image

Generally, the specimen orientations seemed to have the major effect on the mechanical performances of the analysed specimens. However, in some cases, the wall layer number had a slight influence on the obtained results. Considering the UTS, the number of wall layers had a slight enhancing effect, for the sideways and flatwise, especially when considering 2 and 4 wall layers. As previously discussed, the flatwise specimens with 6 wall layers were worse than the ones with 4 wall layers due to the delamination defect occurred during the D&S phases, the lower density and higher value of porosity (5.30%). For the upright group (Fig. 5a), the configuration with 4 wall layers showed the worst mechanical properties with respect to the other two types. This behaviour could be linked to the low value of density and the high value of porosity found through the image analysis (1.80% for upright 2 walls and 4.52% for upright 4 walls). In general, a decrease of density is correlated to a decrease of the mechanical performance. For the sideways group, the increasing of the number of wall layers led to an improvement of the mechanical properties from 2 wall layers to 4 wall layers, while the higher porosity registered in the 6 wall layer configuration (4.05%) decreased this enhancing effect.

Considering the Young’s modulus, the number of wall layers had a worsening effect for the flatwise and sideways, since it reduced the resistance to elastic deformation. Increasing the number of wall layers from 2 to 4, the Young’s modulus decreased by 7% for flatwise specimens and up to 17% for the sideways, while from 4 wall layers to 6 wall layers, the reduction reached 19% for the flatwise and 11% for the sideways. A lower variability affected the upright specimens (reduction of 2% from 2 wall layers to 4 wall layers and 5% from 4 to 6 wall layers), whose values of E were the highest and less variable. These results of uniaxial tensile tests reported worst mechanical properties for the upright specimens with a lower tensile strength and elongation at break compared to the other two specimen orientations. This behaviour was confirmed by other works reported in literature [18, 19, 23] on a BASF Ultrafuse 316L, on 55–60% of 316L stainless steel [6] and on 80% 316L stainless steel and 20% POM [8].

Thus, DIC was also used for better analysing the strain behaviour and the typical anisotropy due to the layerwise geometry of the FFF-printed parts. The influence of the building orientation and number of wall layers was, then, considered more in details. With this aim, the technical strain map was analysed and compared for each combination of orientation and number of wall layers. As it is possible to observe, the technical strain described different colour distributions when varying the specimen orientation, highlighting the mechanical anisotropy of the FFF-printed parts when varying the building direction. Firstly, the upright specimen showed different-coloured bands corresponding to the variation of the technical strain along the longitudinal direction, parallel to the uniaxial load. On the other hand, sideways specimens were characterized by a mostly uniform distribution of technical strain, as highlighted by the coloured map, since the uniaxial force was applied along the filament direction, while flatwise specimens registered a technical strain distribution characterized by a more stressed area in correspondence of the 45° infill pattern.

For each specimen, the most stressed point, which triggers the break, was also detectable from the coloured maps. A longitudinal section was considered for the upright and flatwise specimens (Fig. 10a, c), while a transverse section was considered for the sideways ones (Fig. 10b). Thus, along the sections highlighted in Fig. 10, the Von Mises equivalent strains were obtained with the aim of evaluating the elongation at break considering all the main components, i.e. the entire deformation state of the specimen.

Fig. 10
figure 10

Images acquired with the GOM Aramis system. a Upright specimens with 4 wall layers; b sideways specimens with 4 wall layers; c flatwise specimens with 4 wall layers

Full size image

Considering the upright specimens, Fig. 11 shows the Von Mises equivalent strain evaluated along the longitudinal section for 2, 4 and 6 wall layers. As it is possible to observe from the reported graph, the Von Mises equivalent strain was comprised between 0.20 and 0.40 and, for each number of wall layers, it showed an average variability of 5% along the longitudinal section, resuming the distribution into well-defined colour bands, highlighted from the technical strain coloured map.

Fig. 11
figure 11

Von Mises equivalent strain along the section parallel to load direction for different upright specimens

Full size image

Considering the influence of the wall layer numbers, Fig. 11 shows a range of values comprised between 0.23 and 0.28 for 2 wall layers and between 0.20 and 0.25 for 4 wall layers; the upright with 6 wall layers showed a Von Mises equivalent strain significantly higher (0.32–0.40). The worst behaviour of the 4 wall layers group is confirmed by the high value of porosity detected previously (4.51%) and the lowest density of sintered parts.

Analysing the sideways specimens (Fig. 12), the uniformity of the technical strain map was confirmed by the values of the Von Mises equivalent strain measured along section B (Fig. 10b), with values comprised between 0.24 and 0.44.

Fig. 12
figure 12

Von Mises equivalent strain along the section parallel to load direction for different sideways specimens

Full size image

The specimens with 4 and 6 wall layers were very similar and reported the highest values of Von Mises strain (in the order of 0.40), while 2 wall layer specimens were characterized by significantly lower values, within a range of 0.25–0.27.

Finally, in Fig. 13, the Von Mises equivalent strain for the flatwise specimens is reported with respect to the different wall layers number.

Fig. 13
figure 13

Von Mises equivalent strain along the section parallel to load direction for different flatwise of specimens

Full size image

In this case, there was not a clear distinction between 2, 4 and 6 wall layers, and the values are generally comprised between 0.32 and 0.42. In this regard, it is important to highlight that those sections were drawn in the almost central part of the specimen, which corresponds in all three configurations, to the infill pattern of the specimens. Generally, there was a similar trend between 2 and 4 wall layers, while the specimens with 6 wall layers showed lower Von Mises strain equivalent values, as expected due to the lower density of flatwise six walls specimens and to the delamination defects highlighted in Fig. 9.

As a general conclusion, increasing the number of wall layers can enhance the mechanical properties due to the orientation of the filaments parallel to the applied force direction (in the case of sideways and flatwise specimens). Although, the less strong adhesion wall layer-wall layer and wall layer-infill pattern with respect to the adhesion between the infill pattern rods leads to a higher probability of voids which may cause delamination of the more external walls and thus the reduction of the load bearing section of the specimen, worsening the mechanical characteristics. In the flatwise specimens with 6 wall layers, this aspect affected the UTS and YS, causing a reduction of 5% (405.2 to 387.7 MPa) and 18% (125.7 to 106.7 MPa), respectively. Analysing the surface fracture of the different upright specimens (Fig. 14), the presence of lack of adhesion between wall layers and between wall layers and infill pattern confirmed how these defects affected the performances: considering the UTS average value, increasing the number of walls from 2 to 4 led to a decrease of 9%, due to an increase of porosity. In the sideways specimens, the variation of number of wall layers did not significantly change the mechanical performance and did not cause defects of adhesion or delamination.

Fig. 14
figure 14

Surface fracture of a upright with 2 wall layers and b upright with 4 wall layers

Full size image

To complete the mechanical behaviour analysis, exploiting the advantages of the DIC, the evaluation of Poisson’s ratio (ν) was carried out for each combination of building orientation and number of wall layers (Fig. 15).

Fig. 15
figure 15

Poisson’s ratio in the elastic field for different building orientation and grouped for number of wall layers

Full size image

The average values of the Poisson’s ratio recorded for all combinations were higher than the value of a standard 316L [39] (0.265–0.275). Generally, flatwise specimens showed the highest values of ν; there was a decrease of Poisson ratio between 2 wall layers (0.52 ± 0.04) and 4 wall layers (0.43 ± 0.10), even though the standard deviation increased. On the other hand, there were no relevant differences between 4 and 6 wall layers (0.43 ± 0.08). Considering the sideways, 2 wall layers and 4 wall layers showed almost similar values (0.40 ± 0.06 and 0.40 ± 0.08), while 6 wall layers led to a decrease up to 0.32 ± 0.06. In summary, the upright showed the lowest ν values, with a great variability, compared to the other two types. This behaviour is consistent with the mechanical properties obtained (YS, UTS, E and A), and it is related to the building direction, which is parallel to the uniaxial force applied. Similar relations between building orientation and Poisson’s ratio were found in Gonabadi et al.’s [26] and Henry et al.’s [30] research works. In the upright specimens, the values of Poisson ratio tended to decrease with the increase of the number of wall layers (from 0.41 ± 0.19 to 0.29 ± 0.17). In addition, the values of Poisson ratio obtained reinforced the anisotropic mechanical behaviour of FFF 316L. When subjected under a uniaxial tensile force, the upright behaviour along the specimen is particularly unstable. This is due to the non-uniformity of the strain behaviour registered along the longitudinal direction (see the coloured band distribution on Fig. 10a). This is confirmed by a high deviation standard for each number of wall layers. Thus, it is possible to obtain in some cases a highly variable response of material on the same specimen. In the sideways and flatwise specimens, this variation is slightly lower. Thus, from the obtained results, it appears of paramount importance to evaluate this parameter for a more complete characterization of this material-process combination.

Poisson ratio is generally evaluated in the elastic field; however, there are some cases reported in literature [27], where this parameter was evaluated before the specimen failure (max load), in order to obtain more stable values. In this case, this parameter was evaluated also in the above-mentioned conditions, keeping fixed the wall layer number to 4 (characterized by the highest standard deviations) and analysing the influence of the building orientation. Results, with the respective standard deviations, are reported in Table 4 and compared to the Poisson ratio values computed in the elastic field.

Table 4 Values of the Poisson’s ratio for the different building orientation and same number of wall layers (i.e. 4) in the elastic field and under the maximum load
Full size table

The Poisson ratios corresponding to the max load-condition showed a lower standard deviation confirming what was suggested in the paper of Farfán-Cabrera et al. [27], while the average values were comparable with the ones computed in the elastic field.

5 Conclusions

In this work, the mechanical properties of BASF Ultrafuse 316L were investigated by means of a commercial DIC system, analysing the influence of two different printing parameters, i.e. building orientation and number of wall layers. Therefore, the following conclusions were drawn.

  • From the tensile tests conducted with the aid of the DIC system, the UTS, the YS, E and A were evaluated. The lowest UTS values were registered for the upright specimens due to the layers’ orthogonal orientation with respect to tensile force direction, while flatwise and sideways specimens showed a greater tensile strength, on the order of 400 MPa, but lower if compared to a flat-rolled 316L stainless steel. In particular, flatwise specimens registered an increase of 6.4% for the UTS and an increase of 37.7% of the elongation at break with respect to upright specimens. Furthermore, an increase of 12.8% for UTS and an increase of 31.3% for elongation at break were recorded for the sideways with respect to the upright specimens. The Young’s modulus was higher for the upright, while flatwise and sideways specimens showed a decreasing value of E with the increase of wall layer number. The maximum YS was achieved for the sideways specimens, for every wall layer number, and it was on the order of 130 MPa.

  • From the data provided by the DIC system, it was also possible to determine the Poisson ratio. The evaluation of Poisson’s ratio through the DIC system and the software GOM Aramis reported the highest values for the flatwise and sideways group specimens.

  • Increasing the number of wall layers, the Poisson ratio tended to decrease more consistently for the upright specimens, if compared to flatwise and sideways where the values remained almost constant. The Poisson ratio evaluated under the maximum load condition confirmed the decrease of variability with no relevant changes of the average values.

  • As a general comment, results were greatly affected by the sintered density evaluated on each specimen and by the observed porosity. This aspect was fundamental for explaining some of the obtained results. In this context, the repeatability of the mechanical characteristics of Metal FFF parts is still critical, especially considering high wall layer number due to the higher probability of lack of adhesion between wall layer and wall layer and wall layer and infill pattern. This highlights the influence of 3D printing parameters and the cruciality of the shaping phase in the SDS process chain.

  • Besides the conventional mechanical characterization, data provided by the DIC system allowed to map the strain evolution with respect to the selected printing conditions and deposition strategies. Thus, it was possible to observe how the strain was distributed: in well-defined bands for the upright specimens, along an angle of 45° for the flatwise specimens, while the sideways showed a uniform strain distribution along the tensile load direction. By considering some specific sections, the Von Mises equivalent strain was also evaluated, allowing to assess the deformation state of the specimen by considering all main strain components and obtaining a reliable value of elongation at break. The presented results confirmed that the conventional gauges typically used for the evaluation of mechanical performances of FFF printed parts are sometimes insufficient for describing the complexity of the mechanical and strain behaviour of parts printed by this technology.

This work has to be intended as a contribution to the general knowledge of this novel AM technique. In particular, the evaluation of the Poisson ratio in addition to the main parameters as UTS, YS, E and A, is necessary to obtain more reliable results on a FEM simulator of a part produced via FFF under certain constraints and loads.