1 Introduction

The direct laser metal deposition (DLMD) is an additive manufacturing (AM) technology based on a combination of laser cladding and 3D printing principles [1]. This is usually used to repair and reconfigure worn or damaged components through the application of wear and corrosion-resistant coatings. The laser deposition of metal powders is also particularly suitable to produce metal components with complex geometry or employing innovative materials, extremely difficult to work utilizing traditional techniques. This explains the growing interest of the industry for the DLMD process, mainly in highly specialized manufacturing sectors [2,3,4,5,6,7]. In fact, there are many fields of application of this technology, such as advanced mechanics, aeronautics, aerospace, jewelry, and medicine [8,9,10,11]. The DLMD employs a laser beam (typically Nd:YAG or CO2) to produce a melt pool on a substrate in which is injected a metal material in form of powder or wire. The high temperatures generated during the process allow the melting of the fed material, which contributes to the melt pool growth [12,13,14]. As the laser beam moves, the molten material cools rapidly due to the heat transfer towards the substrate. The solidification front rapidly advances leaving a semi-circular section track of solidified material [15, 16]. The quality of the final parts produced by DLMD, in terms of dimensional accuracy and surface regularity, is strongly affected by many process parameters. For this reason, numerous studies were carried out on process optimization so far [17,18,19,20,21,22,23,24]. Some studies correlated the process parameters to the microstructure and the material properties of the clad [25,26,27,28]. Other research groups focused on improving the deposition efficiency to make the DLMD competitive to other manufacturing processes [29, 30]. The production of thin-walled parts is one of the most exploited DLMD features and is achieved by the superposition of many single tracks, in which the former acts as a base for the subsequent layer. Therefore, the occurrence of localized deposition errors, due to the accidental instability of the powder flow or the laser power, may have a cascading effect on the overall quality of the workpiece. These errors affect the flatness of the deposited surface, changing the standoff distance (or working distance) during the deposition process. The standoff distance, between the nozzle and the substrate surface, is a critical process parameter. In fact, by varying this distance, it is possible to modify the laser spot size and the powder distribution on the deposition plane. If the laser beam collimator is not adjustable, the variation of the standoff distance is the only way to modify the laser defocusing distance, which is the distance between the laser focus and the deposition surface. The study of the effects of these issues on the deposition process and the investigation on the best strategies to mitigate them are crucial.

A series of studies in the literature have investigated the effects of laser focal distance [31], standoff distance [31,32,33], and laser and powder defocusing distance [34] on the geometrical characteristics of the single clad or printed part produced by DLMD process. The results proposed by Ermurat et al. [31] show that a clad of minimum size (in terms of height and width) was obtained by using the highest values (among the levels used for this study) of the standoff distance combined with the value of the laser focal distance that generates the lowest laser spot size on the substrate. Moreover, the clad height is significantly influenced by the standoff distance. In fact, the clad height first rapidly increases and then decreases with the increase in the standoff distance [32, 33, 35]. In the study of Zhu et al. [32], it is shown that the maximum clad height was obtained when the standoff distance was equal to the powder focus distance. In addition, the clad height and its surface quality are significantly affected by the powder and laser defocusing distance parameters. In particular, a high surface quality was obtained when the powder is focused below, and the laser is focused above the top surface of the substrate [34]. The same researchers developed different theoretical mathematical models that allowed the correlation between different process parameters and investigate their effects on the final products [33, 34]. Specifically, Zhu et al. [34] examined the influence of powder and laser defocusing distance on clad height through a mathematical model. The results show that the clad height first increases and then decreases (after reaching the standard position) when the powder defocusing distance goes from a negative to a positive value with respect to the standard distance identified as zero position. On the other hand, the clad height first decreases and then increases when the laser defocusing distance goes from a negative to a positive value with respect to the setup in which the laser is focused on the substrate. Pinkerton and Li [33] developed a model to analyze the temperature distribution near the melt pool and estimate the powder mass deposition rate as a function of standoff distance, while Tan et al. in subsequent works [36, 37] developed theoretical models to simulate the behavior of the powder flow of a multijet coaxial nozzle with four symmetrical tips [36]. They investigated the effects of the powder flow spatial distribution and other process conditions (such as the initial standoff distance and the orientation of the powder flow) on the deposited layer height [37]. The results showed the key influence of the standoff distance on the size of the deposited clad, due to the variation of powder mass concentration on the surface and a good agreement between the experimental measurements and the model results. Also, Eisenbarth et al. [38] investigated the effect of powder flow distribution on the deposited track. They developed a spatial powder flow measurement method and applied it to the two different nozzle geometries, demonstrating the influence of the spatial powder flow on the powder catchment efficiency by the melt pool. Furthermore, for both nozzles, they observed that the highest catchment efficiency was obtained at a value of the standoff distance lower than the geometrical focal length of the powder, owing to the reduced dispersion of the powder stream. Finally, Wang et al. [39] analyzed the improvement of the quality of unequal width parts fabricated by laser direct metal deposition technology through the variation of laser spot diameter.

According to the literature, the effects of some process parameters, such as translation speed, powder feed rate, and laser power on the deposition characteristics, are clear. On the other hand, the literature is ambiguous and reported results that are still not very robust in terms of the combined effects of laser defocusing distance and standoff distance. This work aims to investigate the effects of these significant process parameters on the geometrical characteristics of the single deposited clad. An experimental plan was carried out varying the standoff distance and the laser defocusing distance, and an analysis of variance (ANOVA) on a general linear model was used to assess the statistical significance of the effects. The experimental investigation was performed using a fiber laser source and depositing a particular nickel-based superalloy powder by means of a coaxial nozzle on an AISI 304 stainless-steel substrate. The deposition head equipped with an advanced and innovative motorized optics system allowed the variation of the laser spot size on the substrate surface and consequently the size of the melt pool. This system modifies the characteristics of the laser decoupled to the standoff distance, without changing the laser head position and thus the powder distribution. In order to give an exhaustive explanation of the phenomena, an analytical model to determine the powder distribution and the laser-material interaction was proposed. An experimental setup for the analysis of the spatial powder distribution was realized to validate the results obtained from the analytical model.

In summary, the results showed that the geometrical characteristics of the clad, such as clad width, clad height, penetration depth, and dilution, are affected by standoff distance and laser defocusing distance. The variations of the standoff distance reproduce the roughness of the deposition surface that can be generated during a multilayer deposition or cladding of complex geometries, given by even modest process instabilities (especially of the powder flow) in the underlying layers. Therefore, this work is of paramount importance for an accurate design of these process parameters that can ensure a more stable deposition process with mutable conditions.

2 Experimental conditions and procedure

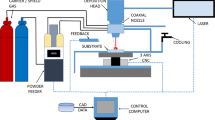
2.1 Setup and materials

Deposition tests were performed on 6-mm-thick AISI 304 stainless steel plates, sized 100 mm (length) × 160 mm (width), which chemical composition is shown in Table 1. A nickel-based superalloy powder was used as deposition material, and the chemical composition is shown in Table 1. The granulometry of the gas atomized powder was in the range of 15–45 μm. The DLMD system included an Ytterbium Laser System YLS 4000 fiber laser source (λ = 1.070 μm), a 5-axis CNC machine, and a powder supply system. The deposition head was equipped with an advanced and innovative motorized optics system. The focal length of the collimation and focusing lenses were respectively 100 mm and 200 mm. The movement of the optics allowed the change of the circular laser spot size on the substrate surface from a diameter of 0.25 to 3.75 mm, without moving the laser deposition head. The laser beam was measured using a rotating pin-hole beam profiler (Primes Focus Monitor). The laser beam was guided from the fiber source to the deposition head through an optical fiber with a diameter of 100 μm. In order to achieve satisfactory processing results and oxide-free depositions, a coaxial Argon gas flow rate of 10 l/min was used to shield the working area. The powder was supplied from an external powder feeder using Argon as carrier gas and was injected into the melt pool through a coaxial nozzle. The tests carried out were characterized through a geometrical analysis of the cross-sections of the clads, which were obtained by trimming them in the transversal direction by means of the Buehler AbrasiMet 250 metallographic cut-off machine. A polishing process was performed, aiming to make the surface of the cross-section highly reflective and free of scratches and deformations. The samples thus prepared were observed by means of a Nikon Eclipse MA200 inverted optical microscope, suitable for micrographic analysis.

Table 1 Chemical composition of the substrate and the powder (wt%)
Full size table

2.2 Experimental plan

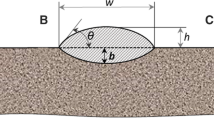
A series of single clad depositions of nickel-based superalloy powder was performed on AISI 304 plates. The controlled process parameters were laser power (P), laser defocusing distance (F), translation speed (v), powder feed rate (Q), carrier gas flow rate (G), and standoff distance (H). Table 2 shows the full factorial experimental plan, with two independent variables: the standoff distance varies over five levels and the laser defocusing distance on three levels. The other process parameters kept constant are listed in Table 3. A total of 15 combinations of process parameters were tested. Five replications were performed for each combination of process parameters. In order to better understand the procedure and the independence of the investigated process parameters, a schematic representation of the experimental setting is displayed in Fig. 1. This experiment allowed an insight into the influence of the two investigated process parameters on the geometrical characteristics of the deposited clads. Each clad was cross-sectioned and analyzed through the optical microscope, as can be seen in Fig. 2. Figure 3 shows the main geometrical characteristics considered in the analysis:

  1. 1.

    Clad width (w)

  2. 2.

    Clad height (hs)

  3. 3.

    Penetration depth (hi)

Table 2 Experimental plan
Full size table
Table 3 Process parameters kept constant in the experimental tests
Full size table
Fig. 1
figure 1

Schematic representation of the process in some employed configurations. a Varying the defocusing distance: (i) F = 17 mm, (ii) F = 25 mm, and (iii) F = 31 mm. b) varying the standoff distance: (i) H = 5 mm, (ii) H = 8 mm, and (iii) H = 11 mm

Full size image
Fig. 2
figure 2

Cross-section macrographs of deposition tests using a H = 5.0 mm and F = 17 mm, b H = 5.0 mm and F = 25 mm, c H = 5.0 mm and F = 31 mm, d H = 6.5 mm and F = 17 mm, e H = 6.5 mm and F = 25 mm, f H = 6.5 mm and F = 31 mm, g H = 8.0 mm and F = 17 mm, h H = 8.0 mm and F = 25 mm, i H = 8.0 mm and F = 31 mm, j H = 9.5 mm and F = 17 mm, k H = 9.5 mm and F = 25 mm, l H = 9.5 mm and F = 31 mm, m H = 11.0 mm and F = 17 mm, n H = 11.0 mm and F = 25 mm, o H = 11 mm and F = 31 mm

Full size image
Fig. 3
figure 3

A typical track cross-section profile with its main geometrical characteristics: clad width (w), clad height (hs), and penetration depth (hi)

Full size image

Another key process parameter that must be controlled for an effective laser deposition process, aimed at both cladding and 3D printing, is the dilution (Dil). It analyzes the ratio between the molten base material and the deposited material and is usually calculated as:

$$Dil= \frac{hi}{(hs+hi)}$$
(1)

In order to assess the statistical significance of the effects of the process parameters on the final quality of the deposited clad, the analysis of variance (ANOVA) on a general linear model was used. The analyzed data set contained the same number of observations for each combination of factor levels.

The proposed experimental plan was also useful to precisely define the mechanism underlying the track formation in the DLMD process. This is a function of two laser-particle interaction modes. There is a mode called “direct” in which the laser beam acts on the powder particles, heating them until melting. On the other hand, there is a mode of track formation known as “indirect” in which the energy supplied by the laser is directed onto the substrate to create a melt pool in which the powder particles will be conveyed. It can be seen from the present work that these two modes are not totally separate and independent. Starting from the analysis of Fig. 2, it can be noticed in the depositions obtained with low standoff values a preponderance of the resolidified area of the substrate caused by the establishment of a large melt pool. However, it can also be seen that this area is extremely limited in depositions obtained using high standoff values. It can be inferred that the first group was originated by indirect mode, in which most of the laser energy reached the substrate, giving rise to a huge melt pool. This subsequently captured the metal particles carried by the gas generating to the track. The second group was originated by a predominantly direct mode. The almost complete absence of a remelted area is a sign of an extremely limited, if not entirely absent, melt pool. However, this did not affect the generation of the clad, which is originated by a direct fusion of the particles by the laser beam and subsequent adhesion to the substrate. Between these two extreme cases, there are depositions produced by a mechanism that is a middle ground between the two aforementioned modes. It can therefore be stated that these modes are not totally distinct, they are instead the extremes of a mechanism of track formation that focuses on the laser-particle interaction. The interaction time between laser beam and metal particles and the spatial distribution of the particles in the region affected by the laser beam play a major role in this mechanism. In the present work, we aimed to study how these features affect the geometrical characteristics of the track. The experimental plan was then developed keeping as constant the carrier gas flow rate for all the proposed cases. In this way, we can assume that the particles exhibit the same velocity for all tests performed, since it is mainly influenced by the carrier gas flow rate. Therefore, the path length of the particles in the volume affected by the laser is crucial for estimating the laser-particle interaction time. By assuming a constant powder flow geometry for all tests, the particle path is a function of the standoff distance, which characterizes the spatial evolution of the powder flow. For instance using high values of standoff distance, the average path of the particles becomes very long, resulting in a longer laser-particle interaction time and consequently a higher absorption/reflection of the laser energy. As previously mentioned, the result of such phenomena is the establishment of a purely direct clad formation mechanism with a melt pool of negligible size.

2.3 Laser beam profile

The laser beam is strongly influenced by laser defocusing distance and standoff distance, which modify its power distribution in the deposition plane corresponding to the substrate surface. In order to evaluate and subsequently compare the effects of F and H parameter on the deposition process, the variation on shape and size of the laser spot was first assessed.

In the setup of the DLMD equipment, the defocusing distance and the standoff distance are independent parameters and both contribute to the determination of the actual laser spot size. Specifically, the defocusing distance is characteristic of the innovative motorized optics system located into the deposition head. This optics system is used for dynamic adaptation of the laser beam during the process. By changing the divergence, the position of the focus point of the laser beam shifts and consequently the way the beam impacts the deposition plane. In this work, the reference values for defocusing distance (Fstd = 17 mm, Fstd = 25 mm, Fstd = 31 mm) are evaluated with respect to the standard deposition plane defined by the manufacturer at a standoff distance of 8 mm from the nozzle.

On the other hand, the standoff distance parameter characterizes the distance between the nozzle outlet and the component surface. The latter concerns the vertical movement of the deposition head, and it can be modified in the equipment keeping the collimator settings unchanged (i.e., the defocusing distance). The interaction between the two process parameters was evaluated using the dedicated collimator software, capable of defining the shape and intensity distribution of the beam in the different planes considered. Figure 4 shows the circular shape of the laser beam used and the Gaussian-like intensity distribution profiles.

Fig. 4
figure 4

Intensity distribution profiles for the laser beam, as a function of radial coordinates and cross-sectional plot

Full size image

The laser beam, like any directional light beam, slightly diverges from the nominal dimension as the distance between the deposition plane and the focus point increases. Figure 5 shows the variation of the laser spot size (defined using the diameter) on the deposition plane as a function of the defocusing distance and standoff distance. It is noticed that the variation of the defocusing distance, obtained through the motorized collimator, has a great influence on the final dimension of the laser spot, while the variation of the standoff distance reveals a limited effect, due to the low divergence of the beam.

Fig. 5
figure 5

Laser spot diameter on the deposition plane with respect to standoff distance

Full size image

2.4 Powder flow distribution

In the DLMD process, the track is obtained by the interaction among the powder flow, the laser beam, and the substrate. Consequently, the spatial distribution of the metal powders assumes considerable importance, to define size, shape, and geometrical characteristics of the clad. In this work, a deep analysis of the powder flow and distribution, produced by means of a coaxial nozzle, was carried out.

The powder distribution is strongly influenced by the geometry of the nozzle, which requires a complex and accurate study to define its characteristics and shape [12]. In order to investigate the powder distribution, a specific experimental setup was developed of which a schematic representation is shown in Fig. 6a. A light source was positioned inside the central cavity of the nozzle, which generates a blue light beam that develops coaxially with the laser beam and the powder flow. An IDS μeye UI-1480SE camera, fitted with a 4.92-megapixel CMOS sensor, was placed transversely to the powder flow and was used to detect the light reflected by the metal particles. Figure 6b shows the blue detection light beam revealing the powder flow leaving the nozzle and defining its conical distribution. The blue light beam resulted imperceptible to the camera in the absence of the powder flow.

The MATLAB® software was used to perform an image analysis on the powder flow detected by means of the detection light. The spatial powder distribution was determined by examining the light reflected by powder particles crossing the light beam. The use of the coaxial light beam, compared to the external orthogonal light beam used by Tan et al. [35,36,37], gives more emphasis on the examination of the deposition region. Furthermore, the reduced focus length and working distance that characterize a coaxial nozzle make the study of a coaxial powder flow even more difficult, compared to the multijet nozzle that adopts longer working distances. The size of the area irradiated by the detection light beam is related to the diameter of the nozzle outlet hole (5 mm) and is considerably larger than that of the laser spot on the deposition surface (about 1–2 mm). Moreover, the convergent conformation of the powder flow concentrates most of particles under the detection light beam, making this setup suitable for the powder flow analysis.

Fig. 6
figure 6

a Schematic representation of the experimental setup and b coaxial nozzle with blue detection light.

Full size image

The first step of the analysis involved a preliminary calibration and an adjustment of the measurements obtained from the phenomena of optical distortion due to perspective. Figure 7 shows the image analysis performed on the median vertical plane (in section line A-A’). By establishing as a reference point the edge of the nozzle, the analysis identified the point of maximum brightness density of the image at a distance of about 8 mm. This is generated by the maximum powder concentration along the median vertical axis, which confirmed the manufacturer requirements of the coaxial nozzle regarding the focus point of the powder flow. The transversal plane passing through this point was defined the standard deposition plane.

Fig. 7
figure 7

Grayscale brightness intensity distribution of the vertical median plane (A-A’ section)

Full size image

The same study was carried out on several transversal planes, highlighted in Fig. 8, identified according to the standoff distances chosen in the experimental plan (ref. Table 2). For the three conidered values of Fstd, the diameters of the laser spot incident the standard deposition plane were plotted using different dotted lines in Fig. 8. These are useful as a reference for identifying the regions of interest of the powder flow for each setup.

Fig. 8
figure 8

Brightness intensity distribution of transversal planes (ref. Table 2) compared to the laser spot size in the standard deposition plane (in dotted lines)

Full size image

The results outlined in Fig. 8 show how the powder distribution profile varies in the considered planes. In the standard deposition plane (8 mm), the powder flow assumes a Gaussian-like distribution, as reported by Tan et al. [35,36,37]. This deposition plane is fundamental for the process because the conjunction between powder flow and laser beam maximizes the powder catchment efficiency by the melt pool.

In planes at 9.5 mm and 11 mm from the nozzle, the powder distribution has a transition from the Gaussian-like distribution to a smooth distribution. Especially for the farthest plane, the profile tends to flatten assuming a nearly constant intensity throughout the size of the light beam.

On the other hand, in the planes closest to the nozzle (6.5 and 5 mm), the powder flow tends to divert sideways. This effect owing to a slight misalignment of the parts that compose the nozzle and that constitute the wall of the cavity in which the coaxial flow is generated. As can be seen, a minimum misalignment has a strong effect on the powder flow close to the cavity. However, this problem is mitigated by approaching the powder focus point. The powder distribution in these planes reaches the maximum intensity laterally with respect to the central axis of the nozzle. This may be the source of the asymmetry of the fused region, which mainly characterizes the depositions realized at such standoff distances (see Fig. 2). Finally, in the closest plane (5 mm), the powder distribution begins to split and show two dissimilar peaks. This depicts the cross-section of the conical flow that characterizes the area closest to the nozzle. The analyses corroborate what was reported in the study of a coaxial powder flow by Eisenbarth et al. [38]. In this work, the axial-symmetrical flow converges from an annulus profile in the region closest to the nozzle to a Gaussian-like profile on the plane of powder focus.

As a first instance, the image analysis was useful to give a qualitative evaluation of the distribution of the powder flow in the different planes. Nevertheless, to determine an appropriate quantitative relationship between the powder mass flow and the brightness profile detected in the image analysis, the brightness spectrum of the entire powder flow was examined. For this purpose, the cumulative relative brightness (CRB) intensity was introduced. The CRB is the integral of brightness values, expressed in grayscale, along a segment belonging to the image plane. In the work, the definition of “summation” was also used because this value was calculated on a variable evaluated in a discreet domain (pixel by pixel), dependent on the resolution of the camera. In the analysis, planes transverse to the direction of propagation of the blue detection light, and the powder flow (which are coaxial) were considered. For each transversal plane along the Z-axis, the CRB was calculated, and the results are plotted in Fig. 9. As expected, planes with the highest brightness intensity were identified close to the nozzle. In fact, the CRB rapidly increases in the first 4 mm beneath the nozzle, due to the converging of powder flow coming from the outer annular cavity. Subsequently, the intensity gradually reduces originates of a descending section of the curve. This interval was evaluated using a linear regression function, reporting a R2 of 0.9884, which certifies the consistency of the descendent part. In the section between the nozzle and the focus point, there is an amount of powder very close to the nominal powder flow. This is completely affected by the light beam, returning a total brightness that can be associated with the nominal amount of powder mass. Assuming a limited variation in powder particles size, and a light reflected by each particle substantially comparable, it is possible to relate the brightness profile with the amount of powder. The maximum brightness value calculated was equal to 3860 and was set as the reference value of the nominal powder flow rate (5.00 g/min). Similarly, the light reflected by the powder was calculated for all the planes and the setup proposed in the experimental plan. This obtained the percentage of powder that was processed.

Fig. 9
figure 9

Cumulative relative brightness (CRB) of transversal planes along the vertical distance from the nozzle

Full size image

The image analysis of the powder flow is structured on the relationship between the powder mass and the light reflected by the particles. The reduction of the CRB along the Z-axis can be traced back to a reduction of powder mass and therefore to the ineffectiveness of the principle of conservation of mass in the analyzed system. The reasons behind this phenomenon were fundamentally attributed to two factors: the determination of the boundaries of the analyzed system and the powder dispersion.

For the first point, it should be specified that the field examined in the image analysis must be considered a portion of the entire closed system, which can ideally be identified with the volume confined by the chamber in which the DLMD operates. In fact, only the region irradiated by the blue detection light is taken into consideration. The boundaries of the system are therefore imposed by the light, but these are not binding for the particles moving inside that can pass through them and leave the field of observation.

The dispersion of powder particles is the second source responsible for the non-conservation of the mass. It originates at the moment in which the flow comes out of the nozzle, passing from being confined by the tube (or from the walls of the nozzle) to being free from external constraints. Taking into account the section of the coaxial powder flow, this is characterized by a certain dispersion of particles that brings off the flow with respect to the direction imposed by the nozzle channel [40]. This dispersion pushes a portion of the particles out of the region irradiated by the blue detection light. This originates a constant mass loss from the region of analysis, which amplifies with increasing the vertical distance in the Z-axis. For these reasons, the system taken into account in the present analysis must be considered open with a constant leaks of particles, dropping the hypothesis of mass conservation. The decrease in the amount of light reflected by the particles is due indeed to the powder dispersion, and it is characteristic of the analyzed powder flow and conditions. In the limited area of analysis, secondary factors such as the mutual shadowing of particles were considered negligible.

Figure 9 indicates the CRB generated by the amount of powder present in the entire area of interest identified by the detection light beam, although merely a fraction of this interacts with the laser beam during processing. In order to establish the amount of powder that is processed during the manufacturing process, the region of interest is compared to the size of the laser spot previously described in Sect. 2.3. Figure 10a shows the CRB produced by the amount of powder in the area affected by the laser spot for each deposition plane related to the standoff distance and defocusing distance adopted in the experimental plan. As the defocusing distance and consequentially the laser spot size incident the deposition plane grows, the interaction area between laser and powder increases. As has already been pointed out in the definition of powder distribution profiles (see Fig. 8), the standoff distance also plays an important role in determining the amount of powder processed by the laser beam. In fact, in the plane at 5.0 mm from the nozzle, the amount of powder incident the laser beam is minimal because the flow focuses outside the region of interest. The powder concentration increases in the plane at 6.5 mm and reaches the highest intensity in the plane at 8.0 mm. In the subsequent planes, it gradually decreases, due to the dispersion of powder flow after the powder focus point.

Fig. 10
figure 10

a CRB produced by the amount of powder in the area affected by the laser spot and b envelope function for each setup of the experimental plan (ref. Table 2)

Full size image

The definition of the mere amount of powder present in the deposition plane does not fully explain the complex laser-particle interactions that occur during the DLMD process. In fact, the powder particles along their path towards the deposition plane interact with the laser beam, absorbing and reflecting its energy. At a greater distance from the nozzle is the deposition plane; a higher number of particles interact with the laser beam for a higher average interaction time. For instance, considering the deposition plane at 11 mm of standoff distance, the powder particles before reaching the deposition point crossed the previous deposition planes (at 5.0 mm, 6.5 mm, 8.0 mm, and 9.5 mm). In order to investigate in deep the mechanics of laser-powder interaction and clad generation, an envelope function of powder distribution profile was proposed.

The envelope function is mainly used in construction theory to define the maximum stresses acting on a structure as the load combination varies [41, 42]. This is also used in some of its variants in failure analysis in geotechnics [43]. In the present work, the principles underlying this function were applied to the case study in order to clarify the effect of laser-particle interaction on the geometrical characteristics of the clad. The analysis of the laser deposition process was approached as a superimposition of different loading profiles. This theory is applicable when the process assumes a stationary state, neglecting the sharp variations of boundary conditions that originate in the transients of the process.

In the determination of the laser-matter relationship, the load profiles in the different deposition planes were determined by means of the powder distribution obtained by the proposed method. With respect to the laser path between the optics and the component surface, the laser encounters load profiles (defined by the powder distribution) in series, from closest to the nozzle outlet to deposition plane profile. The powder particles absorb/reflect the laser energy according to their physical characteristics and spatial distribution, gradually decreasing the useful energy for melting the substrate. The greater the standoff distance, the higher the number of planes are intercepted by the laser beam, each with a different particle distribution. The envelope function is used to obtain the overall load profile that summarized the previously planes encountered by the laser. As shown in Fig. 11, it is given by the maximum brightness value of the powder distribution for each point of the planes considered.

Fig. 11
figure 11

Brightness intensity distribution of transversal planes and envelope function of the deposition plane at standoff distance of 11 mm

Full size image

Thus, the entire spatial development of the powder flow is taken into account, especially in the most remote deposition planes. The regions of interest considered in the upper planes were calculated considering the size of the laser spot on each specific deposition plane as described in Sect. 2.3. The CRB values for each setup were calculated and plotted in Fig. 10b. In this way, the laser-particle interaction were modeled along the entire particle path. Comparing the CRB of each deposition plane to the CRB of the envelope function, it is clear that the latter affect mostly the farther deposition planes that are strongly influenced by previous interactions.

3 Process model

3.1 Modeling of the powder distribution

The theoretical basis on which the whole proposed framework lies is obtained by starting from the hypothesis on the powder distribution stated by Liu and Li [44]. This is expressed according to a Gaussian distribution, and the formulation is given below in Eq. (2):

$$n\left(x,y\right)=\frac{2\dot{{n}_{p}}}{\pi {r}_{p}^{2}}\mathrm{ exp}\left[\frac{-2({x}^{2}+ {y}^{2})}{{r}_{p}^{2}}\right]$$
(2)

where \(n\left(x,y\right)\) is the powder density over the cross-sectional area of the powder flow, \(\dot{{n}_{p}}\) is the powder flow rate, and \({r}_{p}\) the powder flow radius. Liu and Li considered the powder distribution derived from a coaxial nozzle in the plane of the powder focus (also defined as standard deposition plane). This function, while valid for the standard deposition plane, is unable to describe the powder distribution in different deposition planes. As seen in Sect. 2.4, these planes are characterized by distributions with various peaks, which are difficult to model with the classical Gaussian function. Therefore, the function was modified with an annulus function with a Gaussian profile [45], as follows in Eq. (3):

$$n\left(x,y\right)= \frac{2{k}_{p}\dot{{n}_{p}}}{\pi \left[ {{(R+ r}_{pa})}^{2}- {{(R- r}_{pa})}^{2}\right]}\;\mathrm{ exp\;}\left[\frac{-2{(-R+\sqrt{\left({x}^{2}+ {y}^{2}\right)})}^{2}}{{r}_{pa}^{2}}\right]$$
(3)

in which R(z) is the median radius of the annulus (where is positioned the maximum intensity), rpa(z,div) is the half-width of the annular ring (or beam waist), and kp is a calibration factor to ensure the mass conservation in the infinite x–y domain. The median radius is a function of the standoff distance, and it represents the powder distribution of the conical flow of powder. This function is applicable for deposition planes different to the standard deposition plane. In the latter, the function degenerates into the circumference function as proposed by Liu and Li [44]. The half-section of the annulus is a function of the divergence of the powder flow and the standoff distance. The graphs in Fig. 12 represent powder distributions in the deposition planes identified in the experimental plan.

Fig. 12
figure 12

Powder distribution in deposition planes proposed in the experimental plan (ref. Table 2)

Full size image

3.2 Modeling of the laser-material interaction

Once the powder distribution was defined as the standoff distance varied, it was possible to model the laser-matter interaction and the amount of laser energy useful for the creation of the melt pool. By applying the annulus distribution of powder of Eq. (3) in the formulation proposed by Liu and Li [44], the thermal flux density at point (x, y) (I(x, y)) becomes Eq. (4):

$$\begin{aligned}I\left(x,y\right)&={I}_{0}\left(x,y\right)\left[1- \alpha n\left(x, y\right)\right]= \\=\tfrac{2AP}{\pi {r}_{b}^{2}}\;\mathrm{ exp}\left[\tfrac{-2({x}^{2}+ {y}^{2})}{{r}_{b}^{2}}\right]* &\left\{1-\alpha \tfrac{2{{k}_{p}\dot n}_{p}}{\pi \left[{{(R- r}_{pa})}^{2}- {{(R+ r}_{pa})}^{2}\right]}\mathrm{ exp}\left[\tfrac{-2{(R-\sqrt{\left({x}^{2}+ {y}^{2}\right)})}^{2}}{{r}_{pa}^{2}}\right]\right\}\end{aligned}$$
(4)

Consequently, the laser energy absorbed by the workpiece per unit of time (PL) turns into Eq. (5):

$${P}_{L}={\int }_{\Omega }\int I\left(x,y\right)dxdy={\int }_{\Omega }\int {I}_{0}\left(x,y\right)\left[1- \alpha n\left(x,y\right)\right]dxdy=AP-W^{\prime}AP$$
(5)

where the \({W^\prime}\) is:

$$\begin{aligned}{W}^{^{\prime}}&= \alpha \frac{4{k}_{p}\dot{{n}_{p}}}{{\pi }^{2}{r}_{b}^{2}\left[{{(R- r}_{pa})}^{2}- {{(R+ r}_{pa})}^{2}\right]}&\hspace{-8mm}{\int }_{\Omega }\int \mathrm{exp}\left(\frac{-2{(R-\sqrt{\left({x}^{2}+ {y}^{2}\right)})}^{2}}{{r}_{pa}^{2}}-\frac{2({x}^{2}+ {y}^{2})}{{r}_{b}^{2}}\right)dxdy\end{aligned}$$
(6)

Equation (6) represents the fraction of laser energy absorbed/reflected by the powder flow with an annulus distribution. In order to verify the aforementioned equation, a specific region of interaction (Ω) was identified. The region of the laser-material interaction was defined based on the size of the laser beam on the deposition plane. As suggested experimentally, this was coaxial with respect to the powder flow and has a radius smaller than that of the powder distribution (see Fig. 8). The equation used for the region of interaction is expressed in Eq. (7):

$$\Omega =({x}^{2}+ {y}^{2})\le \;{r}_{b}^{2}$$
(7)

where rb(z,div) is the nominal radius of the laser beam that is a function of the standoff distance and the divergence of the laser beam. The three laser spot diameters were evaluated with the respective beam divergence, as previously indicated in Sect. 2.3. The function plotted in Fig. 13 were used as region of interaction (Ω) in which the function was integrated.

Fig. 13
figure 13

Region of interaction for each combination proposed in the experimental plan (ref. Table 2)

Full size image

Figure 14 shows the amount of powder mass interacting with the laser beam calculated applying the proposed formulation for each combination proposed in the experimental plan (Table 2). It is clear how the trend identified using the proposed formulation agree with the experimental results previously shown in Fig. 10a.

Fig. 14
figure 14

Amount of powder interacting with the laser beam for each combination of the experimental plan (ref. Table 2)

Full size image

4 Statistical analysis

The ANOVA with a general linear model was employed to statistically investigate the effects of the two analyzed process parameters on the geometrical characteristics of the single deposited clad. The standoff distance was evaluated at five levels, while the laser defocusing distance was evaluated at three levels. Five replications were performed for each combination of factorial levels. The main effects and the interactions of the investigated factors were analyzed: this represents the average effect of an independent variable and the interaction of two independent variables (as in this case F, H, and F*H) on the dependent variable (w, hs, hi, and Dil). The technique used for the test involved the use of P-value and the significance level α, considered equal to 0.05: when the P-value was less than or equal to α, the effect of the considered factor on the output was statistically significant [17, 22, 24, 46].

Tables 4, 5, 6, and 7 contain the results of the ANOVA analysis. It was found that laser defocusing distance (F), standoff distance (H), and their interaction (F*H) had a statistically significant influence on the clad width, clad height, penetration depth, and dilution. In fact, P-values were very small for all the main effects and their interaction, lower than the limit of significance considered. Thus, it was demonstrated that the considered factors and their interaction influenced the main geometrical characteristics of a deposited clad, justifying further investigations. The importance of a combined analysis of the two factors, that is the main aim of the work, is underlined: this analysis was possible, thanks to the advanced motorized optics system adopted, which allowed the variation of the size of the laser spot on the deposition surface decoupled to the standoff distance.

Table 4 Analysis of variance for clad width (w)
Full size table
Table 5 Analysis of variance for clad height (hs)
Full size table
Table 6 Analysis of variance for penetration depth (hi)
Full size table
Table 7 Analysis of variance for dilution (Dil)
Full size table
Table 8 Physical properties of AISI 304 stainless steel
Full size table

5 Experimental results and discussion

5.1 Effects on the clad width

In laser cladding and 3D manufacturing applications of DLMD technology, an important process variable is the clad width, which mainly is dependent to the melt pool size [47, 48]. In Fig. 15 are shown the effects of the laser defocusing distance (F) and standoff distance (H) variations on clad width (w). The averages of measurements, taken on five replications performed using the same set of process parameters, were used to plot the trends for each combination.

Fig. 15
figure 15

Influence of standoff distance and laser defocusing distance on the clad width

Full size image

Figure 2 shows cross-section macrographs, in which the width of the single deposited clad is modified with the F. This effect is derived from the shift of the laser focus point and so from the spot size variation on the substrate surface. Consequently, increasing F, the laser irradiation area changed, and the interaction time between laser beam and substrate increased, creating a larger molten pool and a clad with a larger width. Similar effects were also deduced from Tan et al. and Zhang et al. [37, 47]. It can also be observed that the standoff distance variance had an impact on the clad width challenging to interpret. Similar considerations have also been indicated in the forecast model of the clad width proposed by Liu and Li [44] and modified by Zhu et al. [34]. The model is the following:

$$w=2{\left(\frac{P A \left(1 -{ r}_{\mathrm{p}}\right) {d}^{1/2}}{2 \left({T}_{\mathrm{m }}- {T}_{0}\right) \sqrt{\pi\; \lambda\; v\; \rho\; {c\;}_{\mathrm{p}}}}\right)}^{1/2}$$
(8)

where P (W) is the laser power, A is the laser absorptivity, rp is the reflectivity factor of powder (from Pinkerton and Li) [33], d (mm) is the laser spot diameter, Tm (K) is the melting temperature, T0 (K) is the initial temperature, λ \((\mathrm W/(\mathrm m\cdot\mathrm K))\) is the coefficient of thermal conductivity, v (m/s) is the laser translation speed, ρ (kg/m) is the density, and cp \((\mathrm J/(\mathrm{kg}\cdot\mathrm K))\) is the specific heat.

However, results found in this experimental work differed from the outcomes obtained through the model shown in Eq. (7) for a calibration coefficient k, which mean value is equal to 0.65. This coefficient originated from the usage of different materials of powder and substrate. Furthermore, it must be said that accurate values of the physical properties of the employed nickel-based superalloy powder were not known because it is covered by copyright. Hence, values of physical properties of the AISI 304 stainless steel at 1000 °C, as listed in Table 8, were used in the model. Of fundamental importance are the temperature values of the process, which were compared with the results obtained from previous experimental tests carried out with the same metal alloy using an IR thermal camera [49].

Following what was stated by Zhu et al. [34], the reflectivity factor of powder related to the Gaussian powder distribution expressed in Eq. (2), here renamed rfp (to avoid mistakes with the powder flow radius rp), reports a value of 0.09. This reflectivity factor of the laser power caused by the metallic powder was experimentally determined [33, 50] by means of an investigation concerning laser cladding. This factor was defined by varying powder feed rate and laser power in a standard configuration of the equipment used. This value of the rfp factor is thus referred to standard deposition conditions. However, as previously stated in Sect. 3, this factor is a function of the powder flow rate and its spatial distribution. Since no experimental values of rfp are available for the W’ of the annulus powder distribution (Eq. (6)) in the literature, in the present work, it was proposed to relate this factor with the Gaussian powder distribution. It was therefore asserted that:

$${rf}_{\mathrm{pi}}= {rf}_{\mathrm{p}}(\frac{{Q}_{i}}{{Q}_{st}})$$
(9)

in which Qi is the powder flow (expressed as CRB) related to the area affected by the laser spot of the considered deposition plane, while Qst as the powder flow related to the area affected by the laser spot in the standard deposition plane (8.0 mm). Both factors are previously reported in Fig. 10a. Therefore, the rfpi proposed in Eq. (8) is the reflectivity factor of the powder referred to the specific deposition condition and is calculated as a proportion between the Qi and Qst. As noted by comparing Figs. 10a and 14, this factor can also be found as ratio between the W’ factor of the annulus powder distribution and the W factor of the Gaussian powder distribution.

Equation (7) for defining the deposited track width w is modified as follows:

$$w={2k\left(\frac{A P \left(1 - {rf}_{\mathrm{pi}}\right) {d}^{1/2}}{2 \left({T}_{\mathrm{m }}- {T}_{0}\right) \sqrt{\uppi \lambda v \rho {c}_{\mathrm{p}}}}\right)}^{1/2}$$
(10)

As can be seen from the model shown in Eq. (9), the clad width is intrinsically affected by the standoff distance and defocusing distance. Some parameters of the equation, proposed by Liu and Li, for the estimation of the clad width are influenced by the standoff distance and the defocusing distance: these are the laser spot diameter (d) and reflectivity factor of powder (rfp). As described in Sect. 2.3, the size of the laser spot on the deposition plane varies as a function of the standoff distance and defocusing distance. From Fig. 5, it can be observed that the laser spot diameter took values from 0.972 to 2.183 mm, which strongly influenced the final clad width.

On the other hand, the laser power reduction factor due to powder reflection should be proportional to the amount and spatial distribution of particles interacting with the energy beam. As shown in Sect. 2.4, this distribution strongly varies with varying the position of the deposition plane. In the closer planes (5.0 mm), the powder flow concentrates on the outer edge of the laser beam, interacting minimally and allowing deeper fusion of the substrate. Inside the melt pool, given the very high thermal gradients, convective motions are generated that lead to the enlargement of the pool. In the intermediate deposition planes (6.5 mm and 8.0 mm), the powder flow is higher and focused more centrally on the region of the laser beam. This leads first to an increased reflection of the laser power by the metal particles and consequently a reduction of the track width. Finally, in the more distant deposition planes (9.5 mm and 11 mm), the particle density drops radically assuming a substantially homogeneous distribution throughout the region of interest. In this way, the track width increases again, primarily because it follows the increase in size of the laser beam and then because the retaining action given by the fusion and mixing with the substrate is reduced. In fact, depositions made with the highest standoff distance result in an extremely low dilution with the substrate, leading to a very low adhesion force between clad and substrate.

Figure 16 shows the calculated values of clad width compared to the measured values. Therefore, a good correlation between the trend of the experimental results and those obtained using the model can be observed. In fact, an average error of 35 µm, 44 µm, and 61 µm was detected for the values related to the defocusing distance of 17 mm, 25 mm, and 31 mm, respectively. This represents an average percentage error of 2.79% and a maximum value of 6.00%. It makes the model suitable for a careful forecast of the clad width.

Fig. 16
figure 16

Comparison between calculated (solid line) and measured (dotted line) values of the clad width

Full size image

5.2 Effects on the clad height

The clad height is another very important geometrical feature of the laser deposition. This geometrical characteristic is important for the control of the fabrication accuracy in the vertical direction [47]. In Fig. 17 are shown the effects of the laser defocusing distance (F) and standoff distance (H) variations on the clad height (hs). Each plotted value is the average of the measures taken on the five replications performed with the same set of process parameters.

Fig. 17
figure 17

Influence of standoff distance and laser defocusing distance on the clad height

Full size image

The influence of laser defocusing distance on clad height was not obvious [51]. In fact, in Fig. 17, it is possible to notice that F had very little influence on the clad height. On the contrary, a strong relationship between clad height and standoff distance can be observed.

The clad height is the geometrical characteristics most linked to the amount of powder injected into the melt pool [17]. The amount of powder and its spatial distribution in the region of interaction with the laser plays a fundamental role in determining the height of the clad. The macrographs analysis (see Fig. 2) was corroborated by the image analysis of the powder flow.

In Fig. 17, it can be observed that the clad height increased very quickly in the transition from H = 5.0 mm to H = 6.5 mm. This phenomenon is caused by the powder flow cutting off: in fact, at such a low standoff distance, the powder cone was truncated by the substrate before focusing. As shown in Fig. 8, the light reflected from the particles in the closer planes to the nozzle reveals a powder concentration in the side areas. Consequently, the laser beam invested less powder during its path and discharged almost all its energy on the substrate creating deposition with lower clad height and higher penetration depth.

When the nozzle moves away from the substrate, the powder flow achieve to focus on the top surface of the substrate. In fact, on the standard deposition plane (8.0 mm), it shows a Gaussian-like distribution, centered in the center of the laser beam. Hence, a greater amount of powder was invested by the laser beam. The substrate returned to be shadowed from the powder flow, and the absorption of the laser energy was better distributed between powder and substrate, increasing the clad height. Hence, the interaction between the laser beam and the powder flow is extremely important [31].

The further increase of H caused the conic powder flow focused to a certain distance above the substrate. In the planes farther from the nozzle, the distribution flattens becoming nearly uniform for the entire surface reached by the energy beam (see Fig. 8). Therefore, after the initial phase in which the clad height increased with the standoff distance, passing the plane in which powder flow focus on the top surface of the substrate, a slight decrease in the clad height was noticed.

The maximum track height was detected at the standoff distance equal to 8 mm (the standard deposition plane), therefore in the plane in which the powder flow focus maximizing the catchment efficiency of the melt pool: the same result was found by Zhu et al. and Tan et al. in their studies [32, 35,36,37].

The amount of powder captured during the processing was calculated by analyzing the envelope function, previously reported in Fig. 10b at different deposition planes and defocusing distances. The relationship between the envelope function and the clad height is presented in Fig. 18. The second-degree regression function exhibits reveals a good correlation between the factors considered, highlighting how the powder flow plays a fundamental role in the clad generation.

Fig. 18
figure 18

Clad height versus cumulative relative brightness (CRB)

Full size image

5.3 Effects on the penetration depth

As stated in the literature [48], the variation of laser defocusing distance and standoff distance affects the characteristics of the melt pool, consequently influencing the penetration depth of the single deposited clad. In Fig. 19 are shown the effects of the laser defocusing distance and the standoff distance variations on the penetration depth.

Fig. 19
figure 19

Influence of standoff distance and laser defocusing distance on the penetration depth

Full size image

It reveals that the penetration depth decreased while the laser defocusing distance increased. A significant parameter, the laser power density, was employed to explain this effect. Equation (10) presents the formulation of laser power density (D).

$$D= \frac{4P}{\uppi {d}^{2}}$$
(11)

D depends on the laser power (P) and the laser spot diameter (d) on the deposition plane. As already asserted in Sect. 2.3, the laser defocusing distance and the standoff distance influence laser spot size incident the deposition plane (see Fig. 5). An increase in both parameters led to an increase of d, hence to a decrease of laser power density, which in turn led to a lower capacity of melting the substrate. This effect caused a decrease in the penetration depth of the melt pool. Quite the opposite, at lower laser spot diameter, the laser power density increased, and the laser power was concentrated in a smaller surface, causing a higher penetration depth. This trend is also discernible in Fig. 2. It shows that low values of standoff distance led to excessive penetration into the substrate. Instead, an increase in standoff distance conducted to a rapid decrease in the penetration depth, which approximately became negligible at high values of standoff distance: the track appeared to be glued to the substrate.

In addition to the influence of energy density, there is another effect to be considered in the analysis of penetration depth: the shadowing effect of metal powders. The particles absorb or reflect part of the energy developed by the laser beam before it reaches the substrate. In this way, the fraction of thermal energy useful to produce the melt pool is reduced as the amount of powder grows, compromising the penetration depth into the base material. In this evaluation, it is essential to take into account both the amount of powder present in the deposition plane and the path taken by the metal particles in the region covered by the laser beam. The particles capture energy all along the path: so, the greater the distance from the deposition plane, the greater the length of the path, the smaller the energy reaches the substrate.

For this analysis, it becomes critical to consider the envelope function developed in Sect. 2.4. This results in an inverse proportionality relationship between the amount of powder passing through the laser beam (considered in terms of CRB) and the penetration depth of the track, as shown in Fig. 20.

Fig. 20
figure 20

Penetration depth versus cumulative relative brightness (CRB)

Full size image

5.4 Effects on the dilution

The dilution assumes a leading role in the quality assessment of DLMD process, especially of dissimilar materials and for determining the adhesion force between clad and substrate. Generally, the optimal value of the dilution parameter is between 10 and 30%.

Since dilution is the ratio of geometrical characteristics discussed above (see Eq. (1)), all the considerations declared on the effects of standoff distance and defocusing distance must be considered. Clearly, the combination and superposition of these effects makes the interpretation of their influences on dilution particularly complex. In Fig. 21, it is noted that the dilution asymptotically decreases with the increase of the standoff distance. For low standoff distance values (5.0 and 6.5), the dilution is considerably high. This is due to the low powder mass captured by the melt pool, which does not allow an adequate growth of the deposited track but enables a large fraction of the laser energy to reach the substrate. On the other hand, the opposite effect is found when the deposition process is carried out with high values of H and the Dil parameter assumes remarkably low values. This makes the process unstable and increases the probability of track detachment due to a poor adhesion with the substrate.

Fig. 21
figure 21

Influence of standoff distance and laser defocusing distance on the dilution

Full size image

As previously demonstrated by the statistical analysis in Sect. 4, the defocusing distance also impacts the dilution value, albeit to a lesser extent. For each value of standoff distance, low values of F produce depositions with progressively higher dilution than the other setups. In fact, as F decreases, the size of the laser spot decreases, and the value of the power density increases (see Eq. 10). Hence, as the defocusing distance increases, the dilution decreases, due to the superimposition of effects on clad and substrate. Combining the influences of standoff distance and defocusing distance on dilution is an excellent way to expand the operating windows of the laser deposition process. The defocusing distance could be increased when the deposition point approaches the nozzle and vice versa, to maintain the dilution values in the acceptability ranges.

The effects on the dilution of the F and H parameters are explained through the analysis of the laser-powder interaction. As for the analysis of the penetration depth, it is essential to take into account the entire path taken by the powders to reach the deposition plane. For this reason, the envelope function presented in Fig. 10b was employed. By relating this function with the dilution values, an excellent correlation between the two parameters with an R2 value of 0.8344 was obtained, as shown in Fig. 22. This is because the image analysis of the powder flow defined the amount of powder which goes to create the deposited track, a fundamental part in the determination of dilution. Moreover, the powder particles passing through the laser beam capture the energy directed to the substrate. This changes the penetration of the laser beam into the base material and consequently the dilution value.

Fig. 22
figure 22

Dilution versus cumulative relative brightness (CRB)

Full size image

6 Conclusions

In this work, a series of experimental tests was carried out by using the direct laser metal deposition (DLMD) process. Nickel-based superalloy powders are convoyed through a coaxial nozzle on AISI 304 stainless steel plates. The effects of laser defocusing distance (F) and standoff distance (H) variations on the geometrical characteristics of the single deposited clad, in terms of clad width, clad height, penetration depth, and dilution, were analyzed. The following conclusions, under the tested conditions, were drawn:

  • An accurate analysis of the influence of standoff distance and defocusing distance on the laser beam profile and powder distribution was carried out. Correlated to the proposed analytical model, the analysis allowed the study of operating conditions with different process setups and correlate them with the geometrical characteristics of the clad.

  • An experimental setup was designed to evaluate the spatial distribution of powder. By means of a coaxial light beam and a laterally positioned camera, it was possible to define the powder distribution in different deposition planes identified by the experimental plan. The cumulative relative brightness (CRB) and envelope function have been proposed to relate the powder flow analysis with the geometrical characteristics of the clad.

  • The relationship between laser defocusing distance, standoff distance, and clad width was studied through an analytical model and experimental measurements. The results of both the experimental tests and the model revealed that an increase of the clad width was obtained as the laser spot size on the deposition plane increased. The effect of standoff distance is more complex to explain and is traced back to the powder distribution that interacts with the laser beam.

  • The variation of the standoff distance led to different heights of the deposited clad. A minimal clad height was detected for lower standoff distances when the powder flow concentrate on the border of the region of interaction with the laser beam. It increases in the standard deposition plane, when the powder focalized in the center of the melt pool, maximizing the powders catchment efficiency. By further increasing of the standoff distance, the clad height reduced again. On the other hand, the laser defocusing distance had a very little influence on the clad height.

  • The penetration depth decreased both with the increase of the laser defocusing distance and the standoff distance. In the first case, it is correlated to a decreasing of the power density on the deposition plane. In the second case, the reason was found in a lower probability of interaction between powders and laser. In fact, for high value of the standoff distance (11.0 mm), the track appeared to be glued or simply lied on the substrate.

  • The dilution follows the same trend of the penetration depth, which is its key factor. As both process parameters increase, the dilution value decreases progressively, because of the combined effects on the penetration depth and clad height. A careful setup of H and F process parameters can be useful to keep the dilution in the optimal range during the DLMD process.