1 Introduction

Considering a standard powder bed fusion (PBF) process, a thin layer of metal powder is deposited onto a part-build area or platform [1]. The laser beam, which is guided by galvano mirrors, scans over the powder bed to form solidified layers, whereas the powder in other areas remains loose. Subsequently, the next powder layer is deposited after the build platform has moved one-layer thickness downwards. The mentioned procedure is repeated, until the final work piece is completely built.

Nickel-base alloy CM247LC is usually used in the aviation field for high-pressure turbine vanes (HPTV), high-pressure and low-pressure turbine blades (HPTB and LPTB, respectively) [2]. Considering the high costs of casting and tooling, especially in case of the cooling systems within the blades with their complex geometry, the aerospace manufacturers have veered towards the laser powder bed fusion (LPBF) technology or selective laser melting (SLM), which eliminates those expensive processes, as reported in [3].

In general, large zones of tensile stresses can be found at the upper zone of prismatic LPBF parts and at the lower part of the used base plate, whereas the upper part of the base plate remains under compressive stresses, before part removal [4]. At the surface of the LPBF-processed part, tensile stresses reach their maximum. In the last layer, stress values reach the same values as the yield stress of the material itself. To reduce residual stresses in LPBF parts and the corresponding distortion, four main strategies can be pursued: tuning the chemical composition, adjusting scan strategies, SLM process and laser parameters, using add-on processes (e.g., powder bed heating and laser shock peening), or post-processes. Often, two and more strategies are combined to achieve a greater reduction in distortion.

In [5], LPBF of pre-alloyed AlSi12 powder and in situ alloyed Al + Si12 at a powder bed pre-heat temperature of 380 °C was compared and while the in situ alloyed powder worked well, powder depositing of pre-alloyed AlSi12 was not possible during LPBF due to agglomeration. Furthermore, with the mixed powder, a stress reduced state throughout the build was created with powder bed pre-heating. Similarly, according to [6], in situ alloying of Al339 (Al-Si-Cu-Mg-Ni), based on pre-alloyed batch blends AlMg and SiCuNi, does not develop significant residual stresses within the process and allows building parts without anchors or supports when powder bed pre-heating is applied.

Island scan strategies with 2 × 2, 3 × 3, 5 × 5, and 7 × 7 mm2 sizes for LPBF-processed IN718 alloy samples result in different residual stress states, as demonstrated in [7]. Considering also the relative density as an additional requirement, the scan strategy with 5 × 5 mm2 size generates the lowest residual stresses. The comparison of different laser scan strategies in [8], continuous (back-and-forth hatching pattern along the entire dimension of the part), and island strategy, for LPBF-processed IN718, clearly shows the highest distortion in the samples with the island strategy, followed by continuous. The results in [9] demonstrate for LPBF of Ti6Al4V that the 90° alternating bi-directional scanning strategy yields less residual stresses during LPBF, compared to chessboard scanning. The residual stresses also increase with increasing chessboard block size. Similar investigations about bi-directional and chessboard scanning are made with LPBF-processed nickel-base alloy 718 in the study of [10]. The bi-directional raster scanning tends to have lower residual stresses compared to the chessboard approach. Generally, the distortion of LPBF-processed cantilevers after lifting off from the platform increases with increasing relative density, as observed for hot working steel 1.2709 in [11]. Furthermore, for this material, a correlation between internal stresses or upon their release distortions and the scan speed was recognized. In case of austenitic stainless steel 1.4404 and Invar 36, [12, 13] reported an increase of residual stresses and distortions with increasing energy density, for all tested scan speeds. Contrary, for LPBF-processed Ti6Al4V samples, the distortions decreased with increased energy density according to [14]. Further information about the development of residual stresses or warp and their reduction via choice of scan strategies or process parameters can be found in [15].

Preheating to temperatures of 550 °C to 570 °C has the main effect on distortion reduction and significantly reduces residual stresses in case of LPBF-processed Ti6Al4V but leads to fast powder degradation, as explained in detail in [14, 16]. In case of LPBF-processed AlSi10Mg, the distortion is reduced to zero at a preheating temperature of 250 °C, independent of the sample thickness, as illustrated in [17]. At 400 °C baseplate temperature, negative deflections of cantilevers are observed for LPBF-processed tool steel 1.2344 (H13), according to the study in [18]. As reported in [19] for stainless steel 1.4540 (PH1) and 1.4404 (316L) LPBF samples, laser shock peening (LSP) effectively changes the residual stress profile from tension to compression. Similarly, high-amplitude compressive residual stresses are introduced into the surface of LPBF-processed IN 625 samples, after solution treatment at 1070 °C for 1 h, followed by water quenching and aging at 720 °C for 18 h, as reported in [20]. By using only the heat treatment approach, the residual stresses of the last-mentioned IN 625 samples are released and close to zero. Barrel finishing (BF), shot peening (SP), ultrasonic shot peening (USP), and ultrasonic impact treatment (UIT) are post processes, which are used for IN 718 LPBF samples in the study of [21]. All the last mentioned post processes result in compressive residual stresses, compared to the LPBF-built specimen. In case of compression, the highest magnitude is achieved with SP, followed by UIT, USP, and BF. In case of LPBF-processed nickel-base alloy 718, heat treatment at 1066 °C for 2 h greatly reduced the residual stresses, as investigated in [10].

To achieve economical LPBF part production combined with high quality in terms of porosity and geometrical accuracy from various materials run in experiments, setup times and efforts for post processing need to be reduced or even avoided. With a second laser beam, a more robust process can be generated. Thus, a second post heating laser source is used in conjunction with a melting laser source in this study, to reduce distortions. This is tested in LPBF processing of CM247LC cantilever samples. A “two bar model” is introduced to explain the generation of residual stresses and their reduction with a multi laser beam offset strategy. Furthermore, re-melting cracks, defects, and microstructure are analyzed in conjunction with the second defocused laser, in case of 200 W.

2 Experimental procedure

2.1 Laser powder bed fusion

For the LPBF process, a gas atomized CM247LC powder from LPW Technology Ltd with a d50 of 40 μm has been used. The chemical composition of the CM247LC powder batch can be found in Table 1. To manufacture the LPBF-processed cantilevers of CM247LC, a flexible laboratory machine with two water-cooled 200 W infrared (1070 nm) fiber lasers and nitrogen atmosphere (oxygen level of 0.5%) is used. Detailed information about the LPBF laboratory machine can be found in [22, 23]. The process parameters from pre-studies, which create dense and crack-free CM247LC samples, as explained in detail in [24], are listed in Table 2, based on the classical definition of the energy density:

Table 1 Chemical composition of CM247LC (wt.%)
Full size table
Table 2 Used process parameters, defined as reference for the LPBF process, referring to Gerstgrasser et al. [24]
Full size table
$$ {\boldsymbol{E}}_{\boldsymbol{d}}=\frac{\boldsymbol{P}}{\boldsymbol{h}\cdotp \boldsymbol{v}\cdotp \boldsymbol{t}} $$
(1)

where Ed is the energy input or energy density in J/mm3, P is the effective laser power in W, h is the hatch distance in mm, and v and t are the laser scan speed in mm/s and layer thickness in mm, respectively.

2.2 Multi laser beam strategy (offset)

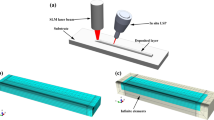
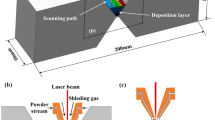
The multi laser beam offset strategy in LPBF with a second defocused laser beam following the first focus spot on the consolidated side with a lateral and longitudinal offset is adopted from the laser welding field. To reduce the internal stresses, this strategy is there implemented with two additional defocused laser beams, as reported in [25]. The schematic top view of the lateral offset strategy with multi laser beams for this LPBF study is shown in Fig. 1 with the additional melt pool dimensions. The small circle in the melt pool image represents the melting laser in the focus plane with a beam diameter of 90 μm and a power of 200 W, whereas the great circle stands for the defocused second laser spot with a diameter of 380 μm for heating. The offset in x-direction xoff is defined as follows, based on geometrical distances in Table 3:

Fig. 1
figure 1

Correctly scaled schematic top view of the offset strategy with corresponding distances, based on equations (2) and (3)

Full size image
Table 3 Pre-test offset parameters with 40 W for the second laser beam, leading to equations (2) and (3)
Full size table
$$ {\boldsymbol{x}}_{\mathbf{off}}=\left(\boldsymbol{h}+\mathbf{10}\ \boldsymbol{\upmu} \mathbf{m}\right)\cdotp \boldsymbol{n} $$
(2)

where n is an augmentation factor. Based on the geometrical distances in Table 3, the lateral offset in y-direction yoff is defined as:

$$ {\boldsymbol{y}}_{\mathbf{off}}=\boldsymbol{n}\cdotp \boldsymbol{h} $$
(3)

The values 3, 6, and 12 are used for n to investigate a non-linear parameter space as pre-test with a laser power of 40 W for a second laser beam. The offset values are listed in Table 3. Finally, the material is processed with the most promising offset parameter and a maximum power of 65 W for the defocused laser beam, to avoid re-melting the bulk material, which would result in re-melting cracks or defects.

2.3 Distortion analysis

In this study, cantilever specimens of CM247LC are manufactured with the LPBF process, since they are widely used to analyze residual stresses or upon partly cutting them off the build platform from one end, the distortions, as reported in [11, 13, 17, 18, 26,27,28,29,30,31,32,33,34]. The geometry of the built specimen cantilever is shown in Fig. 2. After building and cooling down, the relative height Δhbase from the baseplate to the cantilever is measured with a Keyence digital microscope VHX-5000. To avoid the influence of the edges, the relative height is measured on a line lm with 3.5 mm measuring length, 1 mm away from the front edge, and 0.5 mm from the side edges of the 4.5 mm wide cantilever. After cutting off, the height of the measuring line is measured again, giving Δhc, as illustrated in Fig. 3. The average total height difference ∆htot represents the distortion of the cantilever, as follows:

Fig. 2
figure 2

Δhbase, lm, and cantilever dimensions, which are used to measure the distortion

Full size image
Fig. 3
figure 3

Cut cantilever with Δhc

Full size image
$$ \Delta {\boldsymbol{h}}_{\mathbf{tot}}=\frac{\mathbf{1}}{{\boldsymbol{l}}_{\boldsymbol{m}}}{\int}_{\mathbf{0}}^{{\boldsymbol{l}}_{\boldsymbol{m}}}\left[{\boldsymbol{\varDelta} \boldsymbol{h}}_{\boldsymbol{c}}\left(\boldsymbol{\xi} \right)-{\boldsymbol{\varDelta} \boldsymbol{h}}_{\mathbf{base}}\left(\boldsymbol{\xi} \right)\right]\mathbf{d}\boldsymbol{\xi } $$
(4)

The average height Δhbase between the baseplate and the uncut cantilever is illustrated in Fig. 2. Including the distortion of the reference, by using its total height difference, the relative distortion can be obtained as follows:

$$ {\boldsymbol{d}}_{\mathbf{rel}}=\frac{\Delta {\boldsymbol{h}}_{\mathbf{tot}}}{\Delta {\boldsymbol{h}}_{\mathbf{ref},\mathbf{tot}}} $$
(5)

where ∆href, tot is the total height difference of the reference parameter processed cantilever, based on equation (4). Three cantilevers are built and quantified for each offset parameter.

2.4 Re-melting cracks

To demonstrate the influence of the second laser beam on the cracking behavior of CM247LC, the maximum laser power of 200 W (from the laser setup) is applied for the second laser, in conjunction with a higher laser scan speed and a 12.5 % reduced hatch distance. This demonstrates that re-melting cracks are independent of a higher laser scan speed and smaller hatching. As mentioned in Section 2.2, exceeding a laser power of 65 W, in case of the defocused second laser beam results in re-melting cracks. To reduce the offset dimensions, only an offset xoff with 450 μm is applied. The used process parameters, to realize re-melting cracks in a cubic sample with the dimension of 10 × 10 × 10 mm3, are given in Table 4. The XY and XZ plane microsections of the cubic sample are prepared by using a Struers Labotom 5 cutting machine, ATM silicon carbide grinding papers (P120 to P2500), and ATM polishing cloths Zeta with water based, poly crystalline diamond suspension (6, 3, and 1 μm). The re-melting cracks and corresponding defects are obtained from secondary electron signals (SE) images from the XY plane, as shown in Fig. 4a. The SE images of re-melting cracks are compared to an SE image with a classical hot crack (solidification crack) from a sample with increased laser beam diameter of 116 μm from previous work, which leads to hot cracking, as explained in detail in [24]. The comparison should demonstrate the difference in cracking. Electron backscatter diffraction (EBSD) images are taken from the XZ plane, as illustrated in Fig. 4b. A scanning electron microscope (SEM) FEI Quanta 200F is used, to obtain the SE and EBSD images.

Table 4 Parameters used for re-melting crack analysis
Full size table
Fig. 4
figure 4

a Re-melting crack and defect analysis (XY). b EBSD images from the XZ plane

Full size image

3 Results and discussion

The quantified relative distortion values drel of the multi laser beam strategy with a power of 40 W, in case of the heat laser beam, are summarized in Fig. 5. A linear interpolation is applied between the nine average data points, illustrated as a relative distortion surface with an appertaining scale bar on the right-hand side, as shown in Fig. 5. The blue error bars on the data points indicate the corresponding experimental standard deviation, based on the measured relative distortions. In average, all offset parameters result in reduced distortion. Compared to the reference, the biggest difference in relative distortion with a value of about 4.5% is realized by the smallest offsets in x- and y-direction, nearly parallel to the melt beam, and marked as red point with the corresponding value in Fig. 5. The relative distortion surface can be expressed as a two-dimensional process map, where the smallest relative distortion value is marked turquoise, as shown in Fig. 6 (lower left corner). A further increase in power of the heating laser up to a maximum value of 65 W with the smallest offsets xoff and yoff, as given in section 2.2, causes a reduction in relative distortion of more than 7.5%, compared to the results achieved with a power of 40 W. This is illustrated in the chart of Fig. 7.

Fig. 5
figure 5

Relative distortion results from CM247LC cantilevers, manufactured with different offset parameters from Table 3 (logarithmic scale) with a 40 W laser power (second laser)

Full size image
Fig. 6
figure 6

Relative distortion results (CM247LC) from offset strategy as 2D process map (logarithmic scale) with a 40 W laser power (second laser)

Full size image
Fig. 7
figure 7

Further reduction in distortion for CM247LC with increased power up to maximum 65 W for the heat laser beam (second laser)

Full size image

The reduction in distortion with the multi laser beam offset strategy can be explained by the “two bar model,” adapted from the “three bar model” from welding, as reported in [35,36,37]. The “Two bar” model is illustrated in Fig. 8. Both bars have the same geometry. The second bar with stress σS2 represents the actual melt pool region, whereas the first bar with σS1 is defined as the already solidified melt tracks. In the model, the two bars have the same length, and their ends are rigidly connected. Before melting, the bars have equal environmental temperature states, as shown in Fig. 9 on the left-hand side with white bars. Due to heating up with the melt laser beam, the melt pool region bar (second bar) expands and pulls along the first bar, which responds to the thermal expansion of the second bar. The stress σS1 in the first bar has the same amplitude as the stress σS2, just with the opposite sign:

Fig. 8
figure 8

Two bar models, as a simplification to explain the residual stress behavior in LPBF

Full size image
Fig. 9
figure 9

Two bar models, to explain the stress state in LPBF during and after solidification, without multi laser beam offset strategy

Full size image
$$ {\boldsymbol{\sigma}}_{\boldsymbol{S}\mathbf{1}}=-{\boldsymbol{\sigma}}_{\boldsymbol{S}\mathbf{2}} $$
(6)

Hence, the first bar is in tension, whereas the second one is under compression, as illustrated in Fig. 9 (central image) with the orange colored bar. The length of the two bars has to be equal at any time, due to the defined rigid connection, which can be expressed as follows, according to the studies of [36, 37]:

$$ \frac{{\boldsymbol{\sigma}}_{\boldsymbol{S}\mathbf{1}}}{\boldsymbol{E}\left({\boldsymbol{T}}_{\mathbf{0}}\right)}=\frac{{\boldsymbol{\sigma}}_{\boldsymbol{S}\mathbf{2}}}{\boldsymbol{E}\left(\boldsymbol{T}\right)}+\boldsymbol{\alpha} \cdotp \left(\boldsymbol{T}-{\boldsymbol{T}}_{\mathbf{0}}\right) $$
(7)

where T0 is the environmental temperature in this case, T is the elevated temperature, E(T) is the temperature dependent Young’s modulus, and α is the coefficient of thermal expansion. Including the assumed equation (6), equation (7) can be expressed as follows, with respect to the stress in the second bar (assuming transformation of total thermal strain into plastic strain):

$$ {\boldsymbol{\sigma}}_{\boldsymbol{S}\mathbf{2}}=-\boldsymbol{\alpha} \cdotp \left(\boldsymbol{T}-{\boldsymbol{T}}_{\mathbf{0}}\right)\cdotp \frac{\boldsymbol{E}\left({\boldsymbol{T}}_{\mathbf{0}}\right)}{\left(\mathbf{1}+\left[\boldsymbol{E}\left({\boldsymbol{T}}_{\mathbf{0}}\right)/\boldsymbol{E}\left(\boldsymbol{T}\right)\right]\right)} $$
(8)

Since the temperature is quite high in the vicinity of the melting pool, the yield strength of the material drops, and the second bar deforms plastically, as reported in [35]. The second bar pushes the first bar into a compression state, whereas the second bar is now in tension, as illustrated in Fig. 9 on the right-hand side. Using the multi laser beam offset strategy, realized by the second heat laser, the environmental temperature increases, which reduces the temperature difference (T − T0) and the Young’s modulus dependent factor in equation (8), since E(T0) is getting closer to E(T). Reaching a lower stress σS2 in the two bar model leads to less distortion and residual stress in the LPBF part, which can be seen more clearly in the expression of equation (7), regarding the elongation.

The SE SEM images in Fig. 10, obtained from 200 W power in case of the second laser, show different kind of cracks, named “re-melting cracks.” They tend to have a more “chaotic” morphology, compared to the classical solidification or hot cracks, as shown in Fig. 11 and analyzed in [24]. Furthermore, a new kind of defect is identified, which cannot be classified as a typical pore, due to its morphology, as shown in Fig. 12. In Fig. 13, the inverse pole figure (IPF) map for LPBF-processed CM247LC with respect to the Z-axis is illustrated, based on the process parameters in Table 4. Not only the typical fine elongated grains with a strong texture dominated by the preferential alignment of <001> along the Z-axis are discovered, as already reported by [38, 39], but also regions of rather fine and heterogeneously distributed grains. The still preferred crystallographic orientation of <001>{100} can be directly obtained from the pole figures and inverse pole figures, as shown in Fig. 14.

Fig. 10
figure 10

Two different re-melting cracks, in case of 200 W laser power for the second defocused laser

Full size image
Fig. 11
figure 11

Classical hot crack (solidification crack) from a sample with an increased laser beam diameter of approximately 116 μm, which leads to hot cracking, as explained in detail in [24]

Full size image
Fig. 12
figure 12

New kind of defect, which has a different morphology, compared to a classical pore

Full size image
Fig. 13
figure 13

EBSD IPF with respect to the Z-axis for LPBF-processed CM247LC with 200 W for the second offset laser

Full size image
Fig. 14
figure 14

Pole figures 100, 110, and 111 with crystal preferred orientations and inverse pole figures (IPF) with respect to the Z-axis (100), X-axis (010), and Y-axis (001), in case of 200 W for the second offset laser

Full size image

4 Conclusion

The influence of different multi laser beam offset strategies on the distortion of LPBF-processed CM247LC cantilever is investigated. Since pores and cracks act like residual stress annihilators, process parameters, which lead to dense and crack-free samples, are set as reference and used for further distortion investigations and analysis. Comparing the nine different offset parameters to the reference, the following statements can be made:

  • All nine offset parameters in conjunction with the second heat laser beam result in reduced part distortion.

  • The multi laser beam offset strategy is an in situ process approach for direct residual stress reduction, without post-processing, any build chamber heating, or changing the alloy composition. During LPBF, thermal induced residual stresses are one of the critical aspects, especially when it comes to thin walls. A second heat laser beam could lead to new research opportunities for residual stress reduction in critical elements.

  • The multi laser beam offset strategy with a defocused beam diameter of 380 μm for the second heat laser and a maximum power of 65 W, to avoid re-melting cracks, reduces the relative distortion more than 7.5%.

  • The presented “two bar model” represents a simple approach to explain the residual stress behavior and reduction via multi laser beam offset strategy in a vivid and physical way.

  • Further investigations with larger beam diameters and increased laser powers are suggested, because then the heating of the environment is stronger and the revealed effects might increase, without re-melting.

  • In case of an industrial application, cylindrical transverse mode patterns in conjunction with a single melting laser beam during LPBF-processing could be used instead of a second heat laser beam. This opens further research fields in case of residual stress reduction during LPBF with a single laser beam. Generally, the current study demonstrates the potential of local environment heating during LPBF processing.

Furthermore, re-melting defects and microstructure are analyzed, in case of the second defocused offset laser with a laser power of 200 W, an increased laser scan velocity, and a reduced hatch distance. Re-melting cracks tend to have a more “chaotic” morphology, compared to classical hot cracks (solidification cracks). Secondary electron signal (SE) images from the XY plane were taken for the crack comparison. A new kind of defect, which has a different morphology compared to classical pores, has been identified, based on SEM image. In case of the microstructure, not only elongated grains with a strong texture but also regions of rather fine and heterogeneously distributed grains are identified.