Skip to main content
SpringerLink
Log in

Single-axis driven measurement method to identify position-dependent geometric errors of a rotary table using double ball bar

  • ORIGINAL ARTICLE
  • Published:
The International Journal of Advanced Manufacturing Technology Aims and scope Submit manuscript

Abstract

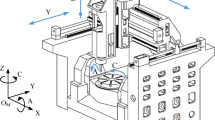
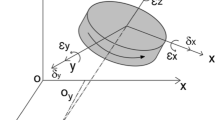
With the development of error compensation technology, reliability and stability of error identification deserve much attention. And rotary axis errors of five-axis machine tool are the main error sources which result in machining inaccuracy. Hence, a new method for position-dependent geometric error (PDGE) identification of a rotary table using double ball bar was proposed in this paper. Especially, only the targeted rotary table was driven during the ball bar test, which can reduce the impact of interference error sources. During the measurement, the ball on the spindle holds still, and the ball on the rotary table rotates around the rotation axis. There are three mounting positions of magnetic socket on the rotary table. Total six measurement procedures of cone test are executed to obtain enough measuring results by setting different positions of magnetic socket ball. These measuring results are used to construct the identification model based on homogeneous transformation matrix (HTM). The impact of installation errors of the double ball bar on identified results was analyzed. The uncertainty of identified errors could be reduced with the single-axis driven and the installation parameter optimization. At last, testing experiments on a five-axis machine tool were conducted to verify the proposed method. The results confirm that the method is an effective way to identify PDGEs of a rotary axis, and the accuracy of identified results is improved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Moriwaki T (2008) Multi-functional machine tool. CIRP Ann Manuf Technol 57(2):736–749

    Article  Google Scholar 

  2. Zhang Y, Yang JG, Zhang K (2013) Geometric error measurement and compensation for the rotary table of five-axis machine tool with double ballbar. Int J Adv Manuf Technol 65:275–281

    Article  Google Scholar 

  3. Wang JD, Guo JJ, Zhou BQ, Xiao J (2012) The detection of rotary axis of NC machine tool based on multi-station and time-sharing measurement. Measurement 45:1713–1722

    Article  Google Scholar 

  4. Zhang ZJ, Ren MJ, Liu MJ, Wu XM, Chen YB (2015) A modified sequential multilateration scheme and its application in geometric error measurement of rotary axis. Procedia CIRP 27:313–317

    Article  Google Scholar 

  5. Jiang ZX, Song B, Zhou XD, Tang XQ, Zheng SQ (2015) Single setup identification of component errors for rotary axes on five-axis machine tools based on pre-layout of target points and shift of measuring reference. Int J Mach Tools Manuf 98:1–11

    Article  Google Scholar 

  6. Ibaraki S, Ota Y (2014) A machining test to calibrate rotary axis error motions of five-axis machine tools and its application to thermal deformation test. Int J Mach Tools Manuf 86:81–88

    Article  Google Scholar 

  7. Ibaraki S, Iritani T, Matsushita T (2012) Calibration of location errors of rotary axes on five-axis machine tools by on-the-machine measurement using a touch-trigger probe. Int J Mach Tools Manuf 58:44–53

    Article  Google Scholar 

  8. Huang ND, Zhang SK, Bi QZ, Wang YH (2016) Identification of geometric errors of rotary axes on 5-axis machine tools by on-machine measurement. Int J Adv Manuf Technol 84(1–4):505–512

    Article  Google Scholar 

  9. Ibaraki S, Iritani T, Matsushita T (2013) Error map construction for rotary axes on five-axis machine tools by on-the-machine measurement using a touch-trigger probe. Int J Mach Tools Manuf 68:21–29

    Article  Google Scholar 

  10. He ZY, Fu JZ, Zhang LC, Yao XH (2015) A new error measurement method to identify all six error parameters of a rotational axis of a machine tool. Int J Mach Tools Manuf 88:1–8

    Article  Google Scholar 

  11. Ibaraki S, Oyama C, Otsubo H (2011) Construction of an error map of rotary axes on a five-axis machining center by static R-test. Int J Mach Tools Manuf 51:190–200

    Article  Google Scholar 

  12. Hong CF, Ibaraki S, Oyama C (2012) Graphical presentation of error motions of rotary axes on a five-axis machine tool by static R-test with separating the influence of squareness errors of linear axes. Int J Mach Tools Manuf 59:24–33

    Article  Google Scholar 

  13. Lau K, Ma Q, Chu X, Liu Y, Olson S (1999) An advanced 6-degree-of-freedom laser system for quick CNC machine and CMM error mapping and compensation. WIT Trans Eng Sci 23:421–434

    Google Scholar 

  14. Chen DJ, Dong LH, Bian YH, Fan JW (2015) Prediction and identification of rotary axes error of non-orthogonal five-axis machine tool. Int J Mach Tools Manuf 94:74–87

    Article  Google Scholar 

  15. Xiang ST, Yang JG, Zhang Y (2014) Using a double ball bar to identify position-independent geometric errors on the rotary axes of five-axis machine tools. Int J Adv Manuf Technol 70:2071–2082

    Article  Google Scholar 

  16. Zargarbashi SHH, Mayer JRR (2006) Assessment of machine tool trunnion axis motion error, using magnetic double ball bar. Int J Mach Tools Manuf 46:1823–1834

    Article  Google Scholar 

  17. Lei WT, Sung MP, Liu WL, Chuang YC (2007) Double ballbar test for the rotary axes of five-axis CNC machine tools. Int J Mach Tools Manuf 47:273–285

    Article  Google Scholar 

  18. Lee KI, Yang SH (2013) Accuracy evaluation of machine tools by modeling spherical deviation based on double ball-bar measurements. Int J Mach Tools Manuf 75:46–54

    Article  Google Scholar 

  19. Tsutsumi M, Saito A (2004) Identification of angular and positional deviations inherent to 5-axis machining centers with a tilting-rotary table by simultaneous four-axis control movements. Int J Mach Tools Manuf 44:1333–1342

    Article  Google Scholar 

  20. Zhu SW, Ding GF, Qin SF, Lei J, Zhuang L, Yan KY (2012) Integrated geometric error modeling, identification and compensation of CNC machine tools. Int J Mach Tools Manuf 52:24–29

    Article  Google Scholar 

  21. Chen JX, Lin SW, He BW (2014) Geometric error measurement and identification for rotary table of multi-axis machine tool using double ballbar. Int J Mach Tools Manuf 77:47–55

    Article  Google Scholar 

  22. Chen JX, Lin SW, Zhou XL, Gu TQ (2016) A ballbar test for measurement and identification the comprehensive error of tilt table. Int J Mach Tools Manuf 103:1–12

    Article  Google Scholar 

  23. Jiang XG, Cripps RJ (2015) A method of testing position independent geometric errors in rotary axes of a five-axis machine tool using a double ball bar. Int J Mach Tools Manuf 89:151–158

    Article  Google Scholar 

  24. Lee KI, Yang SH (2013) Robust measurement method and uncertainty analysis for position-independent geometric errors of a rotary axis using a double ball-bar. Int J Precis Eng Manuf 14(2):231–239

    Article  Google Scholar 

  25. Lee KI, Yang SH (2013) Measurement and verification of position-independent geometric errors of a five-axis machine tool using a double ball-bar. Int J Mach Tools Manuf 70:45–52

    Article  Google Scholar 

  26. Xiang ST, Yang JG (2014) Using a double ball bar to measure 10 position-dependent geometric errors for rotary axes on five-axis machine tools. Int J Adv Manuf Technol 75:559–572

    Article  Google Scholar 

  27. Ding S, Huang XD, Yu CJ, Liu XY (2016) Identification of different geometric error models and definitions for the rotary axis of five-axis machine tools. Int J Mach Tools Manuf 100:1–6

    Article  Google Scholar 

  28. Golub GH, VanLoan CF (2012) Matrix computations, 4th edn. Johns Hopkins University Press, Maryland

    Google Scholar 

  29. Ding S, Huang XD, Yu CJ, Liu XY (2016) Novel method for position-independent geometric error compensation of five-axis orthogonal machine tool based on error motion. Int J Adv Manuf Technol 83(5):1069–1078

    Article  Google Scholar 

Download references

Funding

This work is supported by the National Natural Science Foundation of China (Grant no. 51635003) and is funded by the Research Fund of DMIECT (Grant no. DM201701).

Author information

Authors and Affiliations

  1. College of Mechanical Engineering, Yangzhou University, Yangzhou, 225127, Jiangsu, People’s Republic of China

    Shuang Ding, Weiwei Wu, Aiping Song & Yifu Zhang

  2. School of Mechanical and Power Engineering, Nanjing TECH University, Nanjing, 211816, Jiangsu, People’s Republic of China

    Xiaodiao Huang

Authors
  1. Shuang Ding
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Weiwei Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xiaodiao Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Aiping Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yifu Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shuang Ding.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ding, S., Wu, W., Huang, X. et al. Single-axis driven measurement method to identify position-dependent geometric errors of a rotary table using double ball bar. Int J Adv Manuf Technol 101, 1715–1724 (2019). https://doi.org/10.1007/s00170-018-3086-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00170-018-3086-3

Keywords

Search

Navigation