Skip to main content
SpringerLink
Log in

Regional income club convergence in US BEA economic areas: a spatial switching regression approach

  • Original Paper
  • Published:
The Annals of Regional Science Aims and scope Submit manuscript

Abstract

This study empirically applies the spatial switching regression method to an analysis of regional income club convergence across the 177 economic areas in the contiguous US states over the period from 1969 to 2008. As functionally defined, these economic areas represent the relevant regional markets for labor, products and information. The result of spatial switching regression reveals that the initial gaps between economic areas relative to average global initial per capita income appear to have declined, but the two spatial clubs exhibit a significant difference in their income convergence processes over the period. The estimated coefficient of the convergence parameter for the peripheral spatial regime is negative and highly significant, indicating that a convergence process exists in this spatial regime. However, there is no statistically significant evidence of convergence in the core spatial regime, implying the possibility of different patterns in the growth dynamics of the core spatial regime.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

Notes

  1. The conditional convergence hypothesis suggests that each particular economy approaches its own but unique equilibrium. In contrast, the concept of club convergence is based on models that yield multiple equilibria. In the case of club convergence, regional economies that are identical in their structural characteristics converge to one another in the long run provided that their initial per capita income levels are similar as well (Galor 1996; Islam 2003; Magrini 2004). As Galor (1996) has demonstrated that the assessment of the conditional and the club convergence hypotheses is nearly isomorphic from a neoclassical perspective, the inclusion of empirically significant structural variables (such as human capital, income distribution, fertility, government policies, etc.) strengthens the viability of multiple equilibria and presents club convergence as a competing hypothesis with conditional convergence. In light of this consideration, our empirical analysis focuses on the club convergence hypothesis which suggests that per capita incomes of regional economies with similar structural characteristics converge to one another provided that their initial per capita income levels are similar as well.

  2. Higgins et al. (2006) use the data drawn from 3058 county-level observations. By splitting the large number of observations into two sets of subsamples, they attempt to explore the possible heterogeneity across the US regions. The first set separates the data into 867 metro and 2191 non-metro counties, and the second set separates the data into five regions: the Northeast, Great Lakes, West, Plains and South. However, the role of spatial effects in regional income convergence is virtually ignored in their study on regional income growth and convergence across counties.

  3. Cheshire and Magrini (2000) examine regional growth performance of 122 functionally defined urban regions of the EU of 12 member countries over the period 1978–1994. They are defined on the basis of urban cores identified by concentrations of employment and hinterlands from which commuters flow to the employment core. Niebuhr (2001) investigates regional convergence in West Germany over the period 1976–1996 using the West German planning regions (Raumordnungsregionen) as spatial units of observation. The German planning regions are functionally defined and are composed of several NUTS level-3 regions linked by intensive commuting. Using data on per capita personal incomes in the 172 BEA economic areas over the period 1969–1997, Miller and Genc (2005) provide new insights on the geographical specifications of US regions in the analysis of regional income convergence. However, they do not explicitly consider the role of spatial effects in the process of regional income convergence nor do they examine whether economic areas displaying high or low values of per capita income are randomly distributed across space, or conversely, are clearly concentrated in particular territories.

  4. Johnson and Kort (2004) provide a detailed account of the BEA’s procedures that are used to disaggregate the country into economic areas. The definition of the BEA economic area is based on commuting data from the 2000 decennial census. In less populated parts of the country, newspaper circulation data from the Audit Bureau of Circulations for 2001 are also used to measure the relevant regional markets. The BEA economic areas are defined in three major phases: (i) the identification of economic nodes, (ii) the assignment of counties to BEA component economic areas (CEAs) and (iii) the aggregation of the CEAs to the economic areas. For more specific procedures, see Johnson and Kort (2004).

  5. Following the recommendations of Anselin and Bera (1998) and Getis (2010), we adopt a distance-based contiguity approach based on pure geographical distance due to its unambiguous exogeneity. We use the median as the cut-off parameter above which spatial interactions are assumed to be negligible (Ertur et al. 2006; Ramajo et al. 2008; Chapman et al. 2012). Because the results were robust to the specification of the spatial weights matrix, only the results from the median cut-off value are presented.

  6. This could also imply that part of the positive spatial autocorrelation derives from nuisance spatial dependence, which can result from a mismatch between the spatial boundaries of the growth and convergence processes and the spatial breakdown adopted by BEA. As previously mentioned in Sect. 2, although the BEA economic areas are economically coherent, self-contained spatial units in the contiguous US, these functional regions are dynamic rather than static such that their spatial boundaries may not be fixed in time as economic processes themselves are likely to be evolving over time (Cheshire and Carbonaro 1995; Cheshire and Magrini 2000; Magrini 2004; Rey and Janikas 2005; Fischer and Stirböck 2006).

  7. The Moran scatterplot map may be useful for visualizing atypical localizations, i.e., regions in the HL or LH quadrants of the scatterplot (Anselin 1996). Ord and Getis (1995) suggest the use of the Getis–Ord \(G_i^*\) statistic to detect local “pockets” of dependence that may not show up when using global statistics. Once standardized, a positive value of the Getis–Ord \(G_i^*\) statistic indicates a spatial cluster of high values, whereas a negative value indicates clustering of low values around region i. We use the Getis–Ord \(G_i^*\) statistic to identify spatial regimes in the regional income convergence process in accordance with Fischer and Stirböck (2006) and Gallo and Dall’erba (2006).

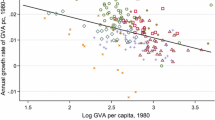
  8. Given the context of \(\beta \)-convergence analysis, we choose to define local spatial association on the logarithm of the initial level of per capita income. As noted by Durlauf and Johnson (1995), the use of split variables which are known at the beginning of the period under study is necessary to avoid the sample selection bias problem that has been pointed out by De Long (1988).

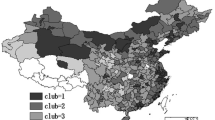
  9. As shown in Fig. 3, the economic areas in Florida also tend to cluster in spatial regime 1, whereas those in North Dakota tend to cluster in spatial regime 2. For the per capita income levels in 2008, spatial regime 1 consists of 76 economic areas, whereas spatial regime 2 is made up of 101 economic areas.

  10. According to the decision rule based on the LM test suggested by Anselin and Florax (1995), if the LM-Lag is more significant than the LM-Error and the robust LM-Lag is significant but the robust LM-Error is not, the appropriate model is the spatial lag model. Conversely, if the LM-Error is more significant than the LM-Lag and the robust LM-Error is significant but the robust LM-Lag is not, the appropriate specification is the spatial error model.

  11. Using data on per capita incomes in the 48 contiguous US states over the period 1929–1994, Rey and Montouri (1999) find an implied convergence rate of 1.8 % per year based on the estimates from the spatial error model.

  12. Using the functionally defined regions as spatial units of observation, Niebuhr (2001) finds strong evidence of substantive spatial dependence in regional income convergence in West Germany. This finding is consistent with our results on substantive spatial dependence.

  13. The empirical studies on regional club convergence draw on formal growth theories in order to construct convergence equations, which in turn are estimated using observations from regional economies. In addition, the choice of convergence clubs is based on a priori theoretical, geographical, economic considerations. As pointed out by Martin and Sunley (1998) and Chapman and Meliciani (2012), however, abstractly theoretical models of convergence may fail to capture the importance of the socio-institutional context and embeddedness of economic geography. Growth and convergence theories need to be spatialized in the sense of recognizing that economic geography can make a contribution to the development of evolutionary economic thinking.

References

  • Anselin L (1988) Spatial econometrics: methods and models. Kluwer, Dordrecht

    Book  Google Scholar 

  • Anselin L (1990) Spatial dependence and spatial structural instability in applied regression analysis. J Reg Sci 30:185–207

    Article  Google Scholar 

  • Anselin L (1996) The Moran scatterplot as an ESDA tool to assess local instability in spatial association. In: Fischer M, Scholten HJ, Unwin D (eds) Spatial analytical perspectives on GIS. Taylor and Francis, London, pp 111–125

    Google Scholar 

  • Anselin L, Florax RJGM (1995) New directions in spatial econometrics: introduction. In: Anselin L, Florax RJGM (eds) New directions in spatial econometrics. Springer, Berlin, pp 3–18

    Chapter  Google Scholar 

  • Anselin L, Bera A (1998) Spatial dependence in linear regression models with an introduction to spatial econometrics. In: Ullah A, Giles DE (eds) Handbook of applied economic statistics. Marcel Dekker, New York, pp 237–289

    Google Scholar 

  • Armstrong HW (1995) An appraisal of the evidence from cross-sectional analysis of the regional growth process within the European Union. In: Armstrong HW, Vickerman RW (eds) Convergence and divergence among European regions. Pion, London, pp 40–65

    Google Scholar 

  • Barca F, McCann P, Rodriguez-Pose A (2012) The case for regional development intervention: place-based versus place-neutral approaches. J Reg Sci 52:134–152

    Article  Google Scholar 

  • Barro RJ, Sala-i-Martin X (1991) Convergence across states and regions. Brook Pap Econ Act 1:107–158

    Article  Google Scholar 

  • Barro RJ, Sala-i-Martin X (1995) Economic growth. McGraw-Hill, New York

    Google Scholar 

  • Baumol WJ (1986) Productivity growth, convergence, and welfare: what the long-run data show. Am Econ Rev 76:1072–1085

    Google Scholar 

  • Baumont C, Ertur C, Le Gallo J (2003) Spatial convergence clubs and the European regional growth process, 1980–1995. In: Fingleton B (ed) European regional growth. Springer, Berlin, pp 131–158

    Chapter  Google Scholar 

  • Carlino G, Mills L (1993) Are U.S. regional incomes converging? J Monet Econ 32:335–346

    Article  Google Scholar 

  • Carlino G, Mills L (1996) Testing neoclassical convergence in regional incomes and earnings. Reg Sci Urban Econ 26:565–590

    Article  Google Scholar 

  • Chapman S, Meliciani V (2012) Income disparities in the enlarged EU: socio-economic, specialization and geographic clusters. Tijdschr Econ Soc Geogr 103:293–311

    Article  Google Scholar 

  • Chapman S, Cosci S, Mirra L (2012) Income dynamics in an enlarged Europe: the role of capital regions. Ann Reg Sci 48:663–693

    Article  Google Scholar 

  • Chatterji M, Dewhurst J (1996) Convergence clubs and relative economic performance in Great Britain. Reg Stud 30:31–40

    Article  Google Scholar 

  • Checherita CD (2009) Variations on economic convergence: the case of the United States. Pap Reg Sci 88:259–279

    Article  Google Scholar 

  • Cheshire P, Carbonaro G (1995) Convergence–divergence in regional growth rates: an empty black box? In: Armstrong HW, Vickerman RW (eds) Convergence and divergence among European regions. Pion, London, pp 89–111

    Google Scholar 

  • Cheshire P, Magrini S (2000) Endogenous processes in European regional growth: convergence and policy. Growth Chang 31:455–479

    Article  Google Scholar 

  • Choi CY (2004) A reexamination of output convergence in the US states: toward which level(s) are they converging? J Reg Sci 44:713–741

    Article  Google Scholar 

  • Cuadrado-Roura JR (2001) Regional convergence in the European Union: from hypothesis to the actual trends. Ann Reg Sci 35:333–356

    Article  Google Scholar 

  • Dall’erba S, Percoco M, Piras G (2008) The European regional growth process revisited. Spat Econ Anal 3:7–25

    Article  Google Scholar 

  • De Long JB (1988) Productivity growth, convergence, and welfare: comment. Am Econ Rev 78:1138–1154

    Google Scholar 

  • De Siano R, D’Uva M (2006) Club convergence in European regions. Appl Econ Lett 13:569–574

    Article  Google Scholar 

  • DiCecio R, Gascon CS (2010) Income convergence in the United States: a tale of migration and urbanization. Ann Reg Sci 45:365–377

    Article  Google Scholar 

  • Durlauf SN (2001) Manifesto for growth econometrics. J Econom 100:65–69

    Article  Google Scholar 

  • Durlauf SN, Johnson PA (1995) Multiple regimes and cross-country growth behavior. J Appl Econom 10:365–384

    Article  Google Scholar 

  • Durlauf SN, Johnson PA, Temple JRW (2009) The methods of growth econometrics, volume 2: Applied econometrics. In: Mills TC, Patterson K (eds) Palgrave handbook of econometrics. Palgrave Macmillan, Hampshire, pp 1119–1179

    Google Scholar 

  • Elhorst JP (2010) Applied spatial econometrics: raising the bar. Spat Econ Anal 5:9–28

    Article  Google Scholar 

  • Ertur C, Le Gallo J (2009) Regional growth and convergence: heterogeneous reaction versus interaction in spatial econometric approaches. In: Capello R, Nijkamp P (eds) Handbook of regional growth and development theories. Edward Elgar, Cheltenham, pp 374–388

    Google Scholar 

  • Ertur C, Le Gallo J, Baumont C (2006) The European regional convergence process, 1980–1995: do spatial regimes and spatial dependence matter? Int Reg Sci Rev 29:3–34

    Article  Google Scholar 

  • Essletzbichler J (2007) Diversity, stability and regional growth in the United States, 1975–2002. In: Frenken K (ed) Applied evolutionary economics and economic geography. Edward Elgar, Cheltenham, pp 203–229

    Google Scholar 

  • Ezcurra R, Rapún M (2007) Regional dynamics and convergence profiles in the enlarged European Union: a non-parametric approach. Tijdschr Econ Soc Geogr 98:564–584

    Article  Google Scholar 

  • Fingleton B (2004) Regional economic growth and convergence: insights from a spatial econometric perspective. In: Anselin L, Florax R, Rey SJ (eds) Advances in spatial econometrics: methodology, tools and applications. Springer, Berlin, pp 397–432

    Chapter  Google Scholar 

  • Fischer M, Stirböck C (2006) Pan-European regional income growth and club-convergence: insights from a spatial econometric perspective. Ann Reg Sci 40:693–721

    Article  Google Scholar 

  • Fotheringham AS, Brunsdon C, Charlton M (2000) Quantitative geography: perspectives on spatial data analysis. Sage, Thousands Oaks

    Google Scholar 

  • Fujita M, Krugman P, Venables AJ (2001) The spatial economy: cities, regions, and international trade. MIT Press, Cambridge

    Google Scholar 

  • Galor O (1996) Convergence? Inferences from theoretical models. Econ J 106:1056–1069

    Article  Google Scholar 

  • Genc IH, Miller JR, Rupasingha A (2011) Stochastic convergence tests for US regional per capita personal income; some further evidence: a research note. Ann Reg Sci 46:369–377

    Article  Google Scholar 

  • Getis A (2010) Spatial autocorrelation. In: Fischer MM, Getis A (eds) Handbook of applied spatial analysis: software tools, methods and applications. Springer, Berlin, pp 255–278

    Chapter  Google Scholar 

  • Hierro M, Maza A (2010) Foreign-born internal migrants: are they playing a different role than natives on income convergence in Spain? Appl Geogr 30:618–628

    Article  Google Scholar 

  • Higgins MJ, Levy D, Young AT (2006) Growth and convergence across the United States: evidence from county-level data. Rev Econ Stat 88:671–681

    Article  Google Scholar 

  • Hobijn B, Franses PH (2000) Asymptotically perfect and relative convergence of productivity. J Appl Econom 15:59–81

    Article  Google Scholar 

  • Islam N (2003) What have we learnt from the convergence debate? J Econ Surv 17:309–362

    Article  Google Scholar 

  • James R, Campbell H (2013) The effects of space and scale on unconditional beta convergence: test results from the United States, 1970–2004. GeoJournal 78:803–815

    Article  Google Scholar 

  • Johnson KP, Kort JR (2004) 2004 Redefinition of the BEA economic areas. Survey of Current Business, November, pp 68–75

  • Krugman P (1991) Geography and trade. MIT Press, Cambridge

    Google Scholar 

  • Krugman P (1998) What’s new about the new economic geography? Oxford Rev Econ Pol 14:7–17

    Article  Google Scholar 

  • Le Gallo J, Dall’erba S (2006) Evaluating the temporal and spatial heterogeneity of the European convergence process, 1980–1999. J Reg Sci 46:269–288

    Article  Google Scholar 

  • Lee K, Pesaran MH, Smith R (1997) Growth and convergence in a multi-country empirical stochastic Solow model. J Appl Econom 12:357–392

    Article  Google Scholar 

  • LeSage J, Fischer MM (2008) Spatial growth regression: model specification, estimation and interpretation. Spat Econ Anal 3:275–304

    Article  Google Scholar 

  • Longhi C, Musolesi A (2007) European cities in the process of economic integration: towards structural convergence. Ann Reg Sci 41:333–351

    Article  Google Scholar 

  • López-Bazo E, Vayá E, Mora AJ, Suriñach J (1999) Regional economic dynamics and convergence in the European Union. Ann Reg Sci 33:343–370

    Article  Google Scholar 

  • Magrini S (2004) Regional (di)convergence. In: Henderson JV, Thisse JF (eds) Handbook of regional and urban economics, volume 4: Cities and geography. Elsevier, Amsterdam, pp 2741–2796

    Google Scholar 

  • Martin R (2001) EMU versus the regions? Regional convergence and divergence in Euroland. J Econ Geogr 1:51–80

    Article  Google Scholar 

  • Martin R, Sunley P (1998) Slow convergence? The new endogenous growth theory and regional development. Econ Geogr 74:201–227

    Article  Google Scholar 

  • Maza A, Villaverde J (2009) Spatial effects on provincial convergence and income distribution in Spain: 1985–2003. Tijdschr Econ Soc Geogr 100:316–331

    Article  Google Scholar 

  • Meliciani V, Peracchi F (2006) Convergence in per-capita GDP across European regions: a reappraisal. Empir Econ 31:549–568

    Article  Google Scholar 

  • Mello M (2011) Stochastic convergence across US states. Macroecon Dyn 15:160–183

    Article  Google Scholar 

  • Miller JR, Genc I (2005) Alternative regional specification and convergence of US regional growth rates. Ann Reg Sci 39:241–252

    Article  Google Scholar 

  • Niebuhr A (2001) Convergence and the effects of spatial interaction. Jahrb Regionalwissen 21:113–133

    Google Scholar 

  • Ord JK, Getis A (1995) Local spatial autocorrelation statistics: distributional issues and an application. Geogr Anal 27:286–306

    Article  Google Scholar 

  • Parr JB (2015) Neglected aspects of regional policy: a retrospective view. Environ Plan C Gov Policy 33:376–392

    Article  Google Scholar 

  • Quah DT (1996) Regional convergence clusters across Europe. Eur Econ Rev 40:951–958

    Article  Google Scholar 

  • Ramajo J, Márquez MA, Hewings GJD, Salinas MM (2008) Spatial heterogeneity and interregional spillovers in the European Union: do cohesion policies encourage convergence across regions? Eur Econ Rev 52:551–567

    Article  Google Scholar 

  • Rey SJ, Montouri BD (1999) U.S. regional income convergence: a spatial econometric perspective. Reg Stud 33:143–156

    Article  Google Scholar 

  • Rey SJ, Janikas MV (2005) Regional convergence, inequality, and space. J Econ Geogr 5:155–176

    Article  Google Scholar 

  • Su J-J (2003) Convergence club among 15 OECD countries. Appl Econ Lett 10:113–118

    Article  Google Scholar 

  • Tsionas EG (2000) Regional growth and convergence: evidence from the United States. Reg Stud 34:231–238

    Article  Google Scholar 

  • Wong DWS, Lee J (2005) Statistical analysis of geographic information with ArcView GIS and ArcGIS. Wiley, Hoboken

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Urban Planning and Engineering, Yonsei University, 50 Yonsei-ro, Seodaemun-gu, Seoul, 03722, Korea

    Up Lim

Authors
  1. Up Lim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Up Lim.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lim, U. Regional income club convergence in US BEA economic areas: a spatial switching regression approach. Ann Reg Sci 56, 273–294 (2016). https://doi.org/10.1007/s00168-015-0739-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00168-015-0739-0

JEL Classification

Search

Navigation