Skip to main content
SpringerLink
Log in

On the formulation of elastic and electroelastic gradient beam theories

  • Original Article
  • Published:
Continuum Mechanics and Thermodynamics Aims and scope Submit manuscript

Abstract

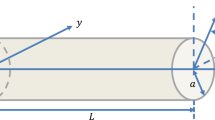
Variational approach for the formulation of gradient beam-type models is discussed. The second gradient elasticity and electroelasticity theories are considered. It is shown that introducing the classical Bernoulli–Euler hypotheses one should take into account the additional boundary conditions on the top and bottom surfaces of the beam to construct the correct gradient beam theory. These boundary conditions are missed in number of works; however, they straightforwardly follow from the variational formulation of the beam-type models as well as from the three-dimensional statement of the boundary value problems of considered gradient theories. Simple example of verification of the correct beam-type models by using semi-inverse analytical solution of a beam pure bending problem is given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Kakunai, S., Masaki, J., Kuroda, R., Iwata, K., Nagata, R.: Measurement of apparent Young’s modulus in the bending of cantilever beam by heterodyne holographic interferometry. Exp. Mech. 25(4), 408–412 (1985)

    Google Scholar 

  2. Lam, D.C., Yang, F., Chong, A., Wang, J., Tong, P.: Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 51(8), 1477–1508 (2003)

    ADS  MATH  Google Scholar 

  3. Liebold, C., Müller, W.H.: Comparison of gradient elasticity models for the bending of micromaterials. Comput. Mater. Sci. 116, 52–61 (2016)

    Google Scholar 

  4. Poncharal, P., Wang, Z., Ugarte, D., De Heer, W.A.: Electrostatic deflections and electromechanical resonances of carbon nanotubes. Science 283(5407), 1513–1516 (1999)

    ADS  Google Scholar 

  5. Stan, G., Ciobanu, C., Parthangal, P.M., Cook, R.F.: Diameter-dependent radial and tangential elastic moduli of zno nanowires. Nano Lett. 7(12), 3691–3697 (2007)

    ADS  Google Scholar 

  6. Li, Z., He, Y., Lei, J., Han, S., Guo, S., Liu, D.: Experimental investigation on size-dependent higher-mode vibration of cantilever microbeams. In: Microsystem Technologies, pp 1–11 (2018)

    Google Scholar 

  7. Eremeyev, V., Altenbach, H.: Basics of mechanics of micropolar shells. In: Altenbach, H., Eremeyev, V. (eds.) Shell-like Structures. CISM International Centre for Mechanical Sciences (Courses and Lectures), vol. 572, pp. 63–111. Springer, Cham (2017)

    Google Scholar 

  8. Altenbach, J., Altenbach, H., Eremeyev, V.A.: On generalized cosserat-type theories of plates and shells: a short review and bibliography. Arch. Appl. Mech. 80(1), 73–92 (2010)

    ADS  MATH  Google Scholar 

  9. Ansari, R., Sahmani, S.: Bending behavior and buckling of nanobeams including surface stress effects corresponding to different beam theories. Int. J. Eng. Sci. 49(11), 1244–1255 (2011)

    MATH  Google Scholar 

  10. Altenbach, H., Eremeev, V., Morozov, N.: On equations of the linear theory of shells with surface stresses taken into account. Mech. Solids 45(3), 331–342 (2010)

    ADS  Google Scholar 

  11. Park, S., Gao, X.: Bernoulli–Euler beam model based on a modified couple stress theory. J. Micromech. Microeng. 16(11), 2355 (2006)

    ADS  Google Scholar 

  12. Papargyri-Beskou, S., Tsepoura, K., Polyzos, D., Beskos, D.: Bending and stability analysis of gradient elastic beams. Int. J. Solids Struct. 40(2), 385–400 (2003)

    MATH  Google Scholar 

  13. Lazopoulos, K., Lazopoulos, A.: Bending and buckling of thin strain gradient elastic beams. Eur. J. Mech. A/Solids 29(5), 837–843 (2010)

    ADS  MathSciNet  Google Scholar 

  14. Eremeyev, V., Aifantis, E.: On extended models of plates based on linear strain gradient elasticity. In: Shell Structures: Theory and Applications, Proceedings of the 11th International Conference (SSTA 2017), vol. 4, pp. 85–88. CRC Press (2018)

  15. Bîrsan, M., Altenbach, H.: On the theory of porous elastic rods. Int. J. Solids Struct. 48(6), 910–924 (2011)

    MATH  Google Scholar 

  16. Sharma, N.D., Maranganti, R., Sharma, P.Ã.: On the possibility of piezoelectric nanocomposites without using piezoelectric materials. J. Mech. Phys. Solids 55, 2328–2350 (2007). https://doi.org/10.1016/j.jmps.2007.03.016

    Article  ADS  MATH  Google Scholar 

  17. Tagantsev, P.V., Yudin, A.K.: Fundamentals of flexoelectricity in solids. Nanotechnology 24(43), 432001 (2013). https://doi.org/10.1088/0957-4484/24/43/432001

    Article  Google Scholar 

  18. Wang, K., Wang, B.: Electrostatic potential in a bent piezoelectric nanowire with consideration of size-dependent piezoelectricity and semiconducting characterization. Nanotechnology 29(25), 255405 (2018). https://doi.org/10.1088/1478-3975/aa9768

    Article  ADS  Google Scholar 

  19. Majdoub, M., Sharma, P., Çağin, T.: Dramatic enhancement in energy harvesting for a narrow range of dimensions in piezoelectric nanostructures. Phys. Rev. B 78(12), 121,407 (2008)

    Google Scholar 

  20. Mindlin, R.D.: Polarization gradient in elastic dielectrics. Int. J. Solids Struct. 4(6), 637–642 (1968)

    MATH  Google Scholar 

  21. Sahin, E., Dost, S.: A strain-gradients theory of elastic dielectrics with spatial dispersion. Int. J. Eng. Sci. 26(12), 1231–1245 (1988)

    Google Scholar 

  22. Kafadar, C.B.: The theory of multipoles in classical electromagnetism. Int. J. Eng. Sci. 9(9), 831–853 (1971)

    MATH  Google Scholar 

  23. Arvanitakis, A.: Gradient effects in a new class of electro-elastic bodies. Zeitschrift für angewandte Mathematik und Physik 69(3), 62 (2018). https://doi.org/10.1007/s00033-018-0959-0

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. Liang, X., Shen, S.: Size-dependent piezoelectricity and elasticity due to the electric field-strain gradient coupling and strain gradient elasticity. Int. J. Appl. Mech. 05(02):1350,015 (2013). https://doi.org/10.1142/S1758825113500154, http://www.worldscientific.com/doi/abs/10.1142/S1758825113500154

    ADS  Google Scholar 

  25. Enakoutsa, K., Vescovo, D.D., Scerrato, D.: Combined polarization field gradient and strain field gradient effects in elastic flexoelectric materials. Math Mech Solids 22(5), 938–951 (2015). https://doi.org/10.1177/1081286515616048

    Article  MathSciNet  MATH  Google Scholar 

  26. Iesan, D.: A theory of thermopiezoelectricity with strain gradient and electric field gradient effects. Eur. J. Mech. A/Solids 67, 280–290 (2018). https://doi.org/10.1016/j.euromechsol.2017.09.007

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. Liu, C., Ll, Ke, Yang, J., Kitipornchai, S., Ys, Wang: Buckling and post-buckling analyses of size-dependent piezoelectric nanoplates. Theor. Appl. Mech. Lett. 6(6), 253–267 (2016). https://doi.org/10.1016/j.taml.2016.10.003

    Article  Google Scholar 

  28. Hadjesfandiari, A.R.: Size-dependent piezoelectricity. Int. J. Solids Struct. 50(18), 2781–2791 (2013). https://doi.org/10.1016/j.ijsolstr.2013.04.020. arXiv:1206.6718

    Google Scholar 

  29. Malikan, M.: Electro-mechanical shear buckling of piezoelectric nanoplate using modified couple stress theory based on simplified first order shear deformation theory. Appl. Math. Modell. 48, 196–207 (2017). https://doi.org/10.1016/j.apm.2017.03.065

    Article  MathSciNet  Google Scholar 

  30. Liang, X., Hu, S., Shen, S.: Effects of surface and flexoelectricity on a piezoelectric nanobeam. Smart Mater. Struct. 23(3), 035,020 (2014)

    Google Scholar 

  31. Shen, S., Hu, S.: A theory of flexoelectricity with surface effect for elastic dielectrics. J. Mech. Phys. Solids 58(5), 665–677 (2010)

    ADS  MathSciNet  MATH  Google Scholar 

  32. Akgöz, B., Civalek, Ö.: Strain gradient elasticity and modified couple stress models for buckling analysis of axially loaded micro-scaled beams. Int. J. Eng. Sci. 49(11), 1268–1280 (2011)

    MathSciNet  MATH  Google Scholar 

  33. Jafari, A., Shah-enayati, S.S., Atai, A.A.: Size dependency in vibration analysis of nano plates; one problem, different answers. Eur. J. Mech. A/Solids 59, 124–139 (2016)

    ADS  MathSciNet  MATH  Google Scholar 

  34. Niiranen, J., Balobanov, V., Kiendl, J., Hosseini, S.: Variational formulations, model comparisons and numerical methods for Euler–Bernoulli micro-and nano-beam models. Math. Mech. Solids 24(1), 312–335 (2017)

    MathSciNet  Google Scholar 

  35. Yang, J.: A review of a few topics in piezoelectricity. Appl. Mech. Rev. 59(6), 335 (2006). https://doi.org/10.1115/1.2345378

    Article  ADS  Google Scholar 

  36. Yan, Z., Jiang, L.: Modified continuum mechanics modeling on size-dependent properties of piezoelectric nanomaterials: a review. Nanomaterials 7(2), 27 (2017). https://doi.org/10.3390/nano7020027

    Article  MathSciNet  Google Scholar 

  37. Mindlin, R.D.: Micro-structure in linear elasticity. Arch. Ration. Mech. Anal. 16(1), 51–78 (1964). https://doi.org/10.1007/BF00248490

    Article  MathSciNet  MATH  Google Scholar 

  38. Dell’Isola, F., Sciarra, G., Vidoli, S.: Generalized hooke’s law for isotropic second gradient materials. In: Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, The Royal Society, pp rspa–2008 (2009)

  39. Polizzotto, C.: A hierarchy of simplified constitutive models within isotropic strain gradient elasticity. Eur. J. Mech. A/Solids 61, 92–109 (2017)

    ADS  MathSciNet  MATH  Google Scholar 

  40. Hu, S., Shen, S.: Electric field gradient theory with surface effect for nano-dielectrics. Comput. Mater. Contin. (CMC) 13(1), 63 (2009)

    Google Scholar 

  41. Yue, Y., Xu, K., Aifantis, E.C.: Strain gradient and electric field gradient effects in piezoelectric cantilever beams. J. Mech. Behav. Mater. 24(3–4), 121–127 (2015)

    Google Scholar 

  42. Yue, Y.M., Xu, K.Y., Aifantis, E.C.: Microscale size effects on the electromechanical coupling in piezoelectric material for anti-plane problem. Smart Mater. Struct. 23(12), 125043 (2014). https://doi.org/10.1088/0964-1726/23/12/125043

    Article  Google Scholar 

  43. Solyaev, Y., Lurie, S.: Numerical predictions for the effective size-dependent properties of piezoelectric composites with spherical inclusions. Compos. Struct. 202, 1099–1108 (2018). https://doi.org/10.1016/j.compstruct.2018.05.050

    Article  Google Scholar 

  44. Lurie, S., Solyaev, Y.: Revisiting bending theories of elastic gradient beams. Int. J. Eng. Sci. 126, 1–21 (2018). https://doi.org/10.1016/j.ijengsci.2018.01.002

    Article  MathSciNet  MATH  Google Scholar 

  45. Askes, H., Aifantis, E.C.: Gradient elasticity in statics and dynamics: an overview of formulations, length scale identification procedures, finite element implementations and new results. Int. J. Solids Struct. 48(13), 1962–1990 (2011)

    Google Scholar 

  46. Gusev, A.A.: Symmetry conditions in strain gradient elasticity. Math Mech Solids 22(4), 683–691 (2015). https://doi.org/10.1177/1081286515606960

    Article  MathSciNet  MATH  Google Scholar 

  47. Lurie, S.A., Volkov-Bogorodsky, D.B., Belov, P., Lykosova, E.: Do nanosized rods have abnormal mechanical properties? on some fallacious ideas and direct errors related to the use of the gradient theories for simulation of scale-dependent rods. Nanosci. Technol. Int. J. 7(4), 261–295 (2016). https://doi.org/10.1615/NanomechanicsSciTechnolIntJ.v7.i4

  48. Gere, J., Timoshenko, S.: Mechanics of materials. PWS-KENT Publishing Company, ISBN 0 534(92174), 4 (1997)

    Google Scholar 

  49. Auffray, N., Le Quang, H., He, Q.C.: Matrix representations for 3D strain-gradient elasticity. J. Mech. Phys. Solids 61(5), 1202–1223 (2013). https://doi.org/10.1016/j.jmps.2013.01.003. arXiv:1301.1890

    ADS  MathSciNet  MATH  Google Scholar 

  50. Auffray, N., Dirrenberger, J., Rosi, G.: A complete description of bi-dimensional anisotropic strain-gradient elasticity. Int. J. Solids Struct. 69–70, 195–206 (2015). https://doi.org/10.1016/j.ijsolstr.2015.04.036

    Article  Google Scholar 

  51. Mindlin, R.D., Eshel, N.N.: On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 4(1), 109–124 (1968). https://doi.org/10.1016/0020-7683(68)90036-X

    Article  MATH  Google Scholar 

  52. Gao, X.L., Park, S.K.: Variational formulation of a simplified strain gradient elasticity theory and its application to a pressurized thick-walled cylinder problem. Int. J. Solids Struct. 44(22–23), 7486–7499 (2007). https://doi.org/10.1016/j.ijsolstr.2007.04.022

    Article  MATH  Google Scholar 

  53. Mindlin, R.D.: Forced thickness-shear and flexural vibrations of piezoelectric crystal plates. J. Appl. Phys. 23(1), 83–88 (1952). https://doi.org/10.1063/1.1701983

    Article  ADS  MathSciNet  MATH  Google Scholar 

  54. Mindlin, R.D.: High frequency vibrations of piezoelectric crystal plates. Int. J. Solids Struct. 8(7), 895–906 (1972). https://doi.org/10.1016/0020-7683(72)90004-2

    Article  MATH  Google Scholar 

  55. Dökmeci, M.C.: A theory of high frequency vibrations of piezoelectric cyrstal bars. Int. J. Solids Struct. 10(4), 401–409 (1974). https://doi.org/10.1016/0020-7683(74)90109-7

    Article  MATH  Google Scholar 

  56. Tiersten, H.: Linear Piezoelectric Plate Vibrations. Springer, Berlin (2013)

    Google Scholar 

  57. Yang, J.S.: Equations for the extension and flexure of a piezoelectric beam with rectangular cross section and applications. Int. J. Appl. Electromagn. Mech. 9, 409–420 (1998)

    Google Scholar 

  58. Krommer, M., Irschik, H.: An electromechanicailly coupled theory for piezoelastic beams taking into account the charge equation of electrostatics. Acta Mech. 154(1–4), 141–158 (2002). https://doi.org/10.1007/BF01170704

    Article  MATH  Google Scholar 

  59. Wang, J., Yang, J.: Higher-order theories of piezoelectric plates and applications. Appl. Mech. Rev. 53(4), 87–99 (2000). https://doi.org/10.1115/1.3097341, http://piezo.nbu.edu.cn/wangji/Papers/AMR00.PDF

    ADS  Google Scholar 

  60. Vidoli, S., Batra, R.C., Dell’Isola, F.: Saint-venant’s problem for a second-order piezoelectric prismatic bar. Int. J. Eng. Sci. 38(1), 21–45 (2000)

    MathSciNet  MATH  Google Scholar 

  61. Giorgio, I., Galantucci, L., Della Corte, A., Del Vescovo, D.: Piezo-electromechanical smart materials with distributed arrays of piezoelectric transducers: current and upcoming applications. Int. J. Appl. Electromagn. Mech. 47(4), 1051–1084 (2015)

    Google Scholar 

  62. Liang, X., Hu, S., Shen, S.: Bernoulli–Euler dielectric beam model based on strain-gradient effect. J. Appl. Mech. 80(4), 044,502 (2013)

    Google Scholar 

  63. Yang, J.: The Mechanics of Piezoelectric Structures. World Scientific, Singapore (2006)

    Google Scholar 

  64. Li, P., Jin, F., Ma, J.: Mechanical analysis on extensional and flexural deformations of a thermo-piezoelectric crystal beam with rectangular cross section. Eur. J. Mech. A/Solids 55, 35–44 (2016). https://doi.org/10.1016/j.euromechsol.2015.08.004

    Article  ADS  MathSciNet  MATH  Google Scholar 

  65. Krommer, M.: On the correction of the Bernoulli–Euler beam theory for smart piezoelectric beams. Smart Mater. Struct. 10(4), 668–680 (2001). https://doi.org/10.1088/0964-1726/10/4/310

    Article  ADS  Google Scholar 

  66. Maurini, C., Dell’Isola, F., Del Vescovo, D.: Comparison of piezoelectronic networks acting as distributed vibration absorbers. Mech. Syst. Signal Process. 18(5), 1243–1271 (2004)

    ADS  Google Scholar 

  67. Solyaev, Y., Lurie, S.: Analytical solution of a plane strain pure bending problem in second gradient electroelasticity. arXiv preprint arXiv:1811.08087 (2018)

  68. Solyaev, Y., Lurie, S.: Pure bending of the piezoelectric layer in second gradient electroelasticity theory (2019) (Submitted)

  69. Alibert, J.J., Seppecher, P., DellIsola, F.: Truss modular beams with deformation energy depending on higher displacement gradients. Math. Mech. Solids 8(1), 51–73 (2003)

    MathSciNet  MATH  Google Scholar 

  70. Seppecher, P., Alibert, J.J., Isola, F.D.: Linear elastic trusses leading to continua with exotic mechanical interactions. J. Phys. Conf. Ser. 319, 012018 (2011)

    Google Scholar 

  71. Baroudi, S., Najar, F., Jemai, A.: Static and dynamic analytical coupled field analysis of piezoelectric flexoelectric nanobeams: a strain gradient theory approach. Int. J. Solids Struct. 135, 110–124 (2018). https://doi.org/10.1016/j.ijsolstr.2017.11.014

    Article  Google Scholar 

  72. Maurini, C., Pouget, J., DellIsola, F.: Extension of the Euler–Bernoulli model of piezoelectric laminates to include 3D effects via a mixed approach. Comput. Struct. 84(22–23), 1438–1458 (2006)

    Google Scholar 

  73. Chroscielewski, J., Schmidt, R., Eremeyev, V.A.: Nonlinear finite element modeling of vibration control of plane rod-type structural members with integrated piezoelectric patches. Contin. Mech. Thermodyn. 31(1), 147–188 (2019)

    ADS  MathSciNet  Google Scholar 

  74. Girchenko, A., Eremeyev, V., Morozov, N.: Modeling of spiral nanofilms with piezoelectric properties. Phys. Mesomech. 14(1), 10 (2011)

    Google Scholar 

Download references

Funding

This work was supported by the IAM RAS basic program AAAA-A19-119012290177-0.

Author information

Authors and Affiliations

  1. Institute of Applied Mechanics of Russian Academy of Sciences, Moscow, Russia

    Sergey Lurie & Yury Solyaev

Authors
  1. Sergey Lurie
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yury Solyaev
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sergey Lurie.

Ethics declarations

Conflicts of interest

The authors declare that they have no conflict of interest.

Additional information

Communicated by Victor Eremeyev and Holm Altenbach.

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lurie, S., Solyaev, Y. On the formulation of elastic and electroelastic gradient beam theories. Continuum Mech. Thermodyn. 31, 1601–1613 (2019). https://doi.org/10.1007/s00161-019-00781-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00161-019-00781-3

Keywords

Search

Navigation