Topology optimization of self-supporting infill structures

Abstract

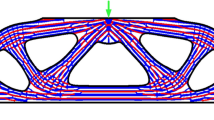
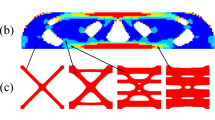
This paper presents a density-based topology optimization approach to design self-supporting and lightweight infill structures with efficient mechanical properties for enclosed structural shells. A new overhang constraint is developed based on the additive manufacturing (AM) filter to ensure that the infills are not only self-supporting in a specified manufacturing direction but can also provide necessary supports to the external shell for successful manufacturing. Two-field–based parametrization and topology optimization formulations are used to impose minimum length scales and to avoid the impractical design solutions that exhibit one-node connection structural members. Besides, a localized volume constraint is utilized to achieve a porous infill pattern. By solving the optimization problem, a shell-infill design can be obtained with very few overhang elements that can be easily post-processed without affecting the mechanical properties of the overall structure. As a result, the optimized design contains no overhang elements and exhibits a better mechanical property than that with predefined periodic infill patterns of the same weight. Numerical examples are given to demonstrate the effectiveness and applicability of the proposed approach.

Appendix

The sensitivity of the overhang constraint function G in (10) is calculated by the chain rule:

$$ \frac{dG}{d\phi_{e}} =\sum\limits_{m,n,i=1}^{M} \frac{\partial G}{\partial\check{\phi}_{m}}\cdot \frac{\partial\check{\phi}_{m}}{\partial\bar{\phi}_{n}}\cdot \frac{\partial\bar{\phi}_{n}}{\partial\tilde{\phi}_{i}}\cdot \frac{\partial\tilde{\phi}_{i}}{\partial\phi_{e}}, $$

(21)

where M is the total number of element in the building chamber Ω^∗. $\frac {\partial \check {\phi }_{m}}{\partial \bar {\phi }_{n}}$, $\frac {\partial \bar {\phi }_{n}}{\partial \tilde {\phi }_{i}}\cdot$, $\frac {\partial \tilde {\phi }_{i}}{\partial \phi _{e}}$ are given as followed:

$$ \frac{\partial\check{\phi}_{m}}{\partial\bar{\phi}_{n}} = \left\{ \begin{array}{ll} 1 & m=n \quad and \quad m \in {\Omega}\\ 0 & otherwise \end{array}, \right. $$

(22)

$$ \frac{\partial\bar{\phi}_{n}}{\partial\tilde{\phi}_{i}}= \left\{ \begin{array}{ll} \frac{\beta(1-{tanh}^{2}(\beta(\tilde{\phi}_{i}-\eta)))}{tanh(\beta \eta)+tanh(\beta(1-\eta))} & n=i\\ 0 & n \neq i \end{array}, \right. $$

(23)

$$ \frac{\partial\tilde{\phi}_{i}}{\partial\phi_{e}}= \left\{ \begin{array}{ll} \frac{H_{ei}}{{\Sigma}_{j \in B_{i,r}}H_{ij}} & i,e \in {\Omega} \\ 0 & otherwise \end{array}. \right. $$

(24)

Besides, $\frac {\partial G}{\partial \check {\phi }_{m}}$ is calculated as follows:

$$ \begin{array}{lll} \!\!\frac{\partial G}{\partial\check{\phi}_{m}} \!&=&\!\displaystyle\sum\limits_{j=1}^{M} \frac{\partial G}{\partial(\check{\phi}_{j}-\hat{\phi}_{j})} \frac{\partial(\check{\phi}_{j}-\hat{\phi}_{j})}{\partial\check{\phi}_{m}}\\ \!&=&\!\displaystyle\sum\limits_{j=1}^{M} \frac{\partial ({\sum}_{i\in {\Omega}^{*}} max\{(\check{\phi}_{i}-\hat{\phi}_{i}),0\}^{2})}{\partial(\check{\phi}_{j}-\hat{\phi}_{j})} V_{e} (\frac{\partial\check{\phi}_{j}}{\partial\check{\phi}_{m}} - \frac{\partial\hat{\phi}_{j}}{\partial\check{\phi}_{m}})\\ \!&=&\!\displaystyle\sum\limits_{j=1}^{M} 2max\{(\check{\phi}_{j}-\hat{\phi}_{j}), 0 \}V_{e} (\frac{\partial\check{\phi}_{j}}{\partial\check{\phi}_{m}} - \frac{\partial\hat{\phi}_{j}}{\partial\check{\phi}_{m}})\\ \!&=&\!2max\{(\check{\phi}_{m}-\hat{\phi}_{m}), 0 \}V_{e} -2 V_{e} \displaystyle\sum\limits_{j=1}^{M} max\{(\check{\phi}_{j}-\hat{\phi}_{j}), 0 \} \frac{\partial\hat{\phi}_{j}}{\partial\check{\phi}_{m}} \end{array} $$

(25)

where ${\sum }_{j=1}^{M} max\{(\check {\phi }_{j}-\hat {\phi }_{j}), 0 \} \frac {\partial \hat {\phi }_{j}}{\partial \check {\phi }_{m}}$ can be calculated by the formulation in Langelaar (2017).

The finite difference check for the sensitivity of the overhang constraint is plotted in Fig. 16, where the horizontal axis is the disturbance in one of the design variables, the vertical axis is the relative error between the sensitivity calculated by (21)–(25), and the sensitivity calculated by finite difference.

Fig. 16

The finite difference check for the sensitivity of the overhang constraint. aΔϕ > 0; bΔϕ < 0