Structural optimization considering dynamic reliability constraints via probability density evolution method and change of probability measure

Abstract

The present paper presents a framework for solving dynamic reliability–based design optimization (DRBDO) problems. The proposed approach is based on a sequential approximate programming technique, where the solution of the original design problem is obtained by converting it into a sequence of sub-optimization problems with a simple explicit algebraic structure. The technique is combined with the probability density evolution method (PDEM) for the purpose of estimating the reliability and/or the failure probability at the different designs in an efficient manner. The change of probability measure (COM), a strategy based on the Radon-Nikodym derivative, is employed to estimate the sensitivity information required by the optimization scheme. Based on this strategy, the sensitivity information can be obtained without any additional function evaluation. Thus, the numerical efforts associated with the reliability assessment and sensitivity analysis can be considerably reduced. The results of the numerical examples indicate that the proposed method is an effective and efficient tool for solving a class of DRBDO problems.

Appendices

Appendix 1

Generally, four steps are involved in the solution of the generalized density evolution equation (GDEE)

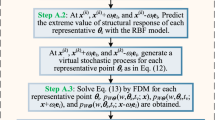
• Step A.1: Discretize the probability-assigned space, Ω_Θ, by the optimal point selection strategy, e.g., the GF discrepancy minimization-based method (Chen and Chan 2019; Chen et al. 2016; Chen and Zhang 2013). The selected point set is denoted by ${\mathcal{P}}_{\mathrm{sel}}=\left\{\left.\left({\boldsymbol{\theta}}_q,{P}_q\right)\right|q=1,2,\cdots, {n}_{\mathrm{sel}}\right\}$, in which n_sel is the number of representative points and θ_q = (θ_{1, q}, θ_{2, q}, ⋯, θ_{s, q}) is the qth representative point with assigned probability

$$ {P}_q={\int}_{V_q}{p}_{\boldsymbol{\varTheta}}\left(\boldsymbol{\theta} \right)\mathrm{d}\boldsymbol{\theta } $$

(34)

where V_q stands for the representative domain determined by the Voronoi cell (Li and Chen 2009) of the representative point θ_q.

• Step A.2: Perform the dynamic analysis of the system to obtain the velocity response $\dot{Z}\left({\boldsymbol{\theta}}_q,t\right)$ for each representative point θ_q, q = 1, 2, ⋯, n_sel.

• Step A.3: For each representative point θ_q, introduce the corresponding velocity response $\dot{Z}\left({\boldsymbol{\theta}}_q,t\right)$ into the GDEE, i.e., (11). Solve the equation by the finite difference method with total variation diminishing (TVD) scheme (Li and Chen 2004). The initial condition for the representative point θ_q is

$$ {\left.{p}_{Z\boldsymbol{\varTheta}}\left(z,{\boldsymbol{\theta}}_q,t\right)\right|}_{t=0}=\delta \left(z-{z}_0\right){P}_q $$

(35)

• Step A.4: Obtain the instantaneous PDF of the response Z(θ, t) by synthesizing all the results related to the representative points

$$ {p}_Z\left(z,t\right)={\int}_{\varOmega_{\boldsymbol{\varTheta}}}{p}_{Z\boldsymbol{\varTheta}}\left(z,\boldsymbol{\theta}, t\right)\mathrm{d}\boldsymbol{\theta } =\sum \limits_{q=1}^{n_{\mathrm{sel}}}{p}_{Z\boldsymbol{\varTheta}}\left(z,{\boldsymbol{\theta}}_q,t\right) $$

(36)

In the present paper, the above point-evolution pathway is adopted. A detailed implementation of the solution of the GDEE can be found in (Chen et al. 2016; Chen and Zhang 2013; Li and Chen 2004; Li and Chen 2009). It is noteworthy that the GDEE can also be solved in the ensemble-evolution pathway (Li et al. 2012; Tao and Li 2017).

Appendix 2

The error estimation of the PDEM is established by an extension of Koksma-Hlawka inequality (Chen and Chan 2019; Chen et al. 2016; Chen and Zhang 2013)

$$ \left|R(f)-Q\left(f,{\mathcal{P}}_{\mathrm{sel}}\right)\right|\le \mathrm{TV}(f)\cdot {D}_{\mathrm{EF}}\left({\mathcal{P}}_{\mathrm{sel}}\right) $$

(37)

in which f(⋅) is a function representing the stochastic system; ${\mathcal{P}}_{\mathrm{sel}}=\left\{\left.\left({\boldsymbol{\theta}}_q,{P}_q\right)\right|q=1,2,\cdots, {n}_{\mathrm{sel}}\right\}$ denotes the representative point set and the corresponding assigned probabilities; R(f) is a probabilistic integral and it stands for the reliability in the present paper; $Q\left(f,{\mathcal{P}}_{\mathrm{sel}}\right)$ is the reliability evaluated by the PDEM; TV(f) is a measure of the irregularity of the function f with respect to its arguments, and it remains constant for a given f; and ${D}_{\mathrm{EF}}\left({\mathcal{P}}_{\mathrm{sel}}\right)$ is the EF-discrepancy which is a measure of the uniformity of the point set.

In the present formulation, representative points are selected by the GF-discrepancy minimization-based method. The relationship between the EF-discrepancy and GF-discrepancy takes the form (Chen and Chan 2019):

$$ {D}_{\mathrm{GF}}\left({\mathcal{P}}_{\mathrm{sel}}\right)\le {D}_{\mathrm{EF}}\left({\mathcal{P}}_{\mathrm{sel}}\right)\le 3.635{D}_{\mathrm{GF}}\left({\mathcal{P}}_{\mathrm{sel}}\right) $$

(38)

where ${D}_{\mathrm{GF}}\left({\mathcal{P}}_{\mathrm{sel}}\right)$ denotes the GF-discrepancy of the representative point set.

Therefore, the less is the GF-discrepancy of the representative point set, the less is the error in the reliability assessment. In general, the GF-discrepancy decreases when the number of representative points increases. As a result, the evaluation of reliability will become more accurate when more representative points are involved.

For a full description on EF-discrepancy, GF-discrepancy, extended Koksma-Hlawka inequality and the error estimation of the PDEM, the reader is referred to (Chen and Chan 2019).

Replication of results

Data in the present manuscript are available by request for the replication of results.