Time-dependent reliability analysis through projection outline-based adaptive Kriging

Abstract

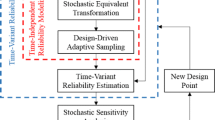
Time-dependent reliability analysis (TRA) has drawn much attention due to its ability in measuring the probability that a system or component keeps safe in the full life cycle. Since it is difficult to efficiently obtain accurate results for TRA problems with expensive simulation demand, many surrogate model-based methods have been proposed to handle this challenge. Moreover, when both random and interval uncertainties are included in these TRA problems simultaneously, the analysis process will be more complicated. In this paper, two methods based on projection outline adaptive Kriging (POK) are proposed to handle TRA and TRA with mixed interval uncertainties (iTRA), respectively. Firstly, POK-TRA method is put forward for the TRA problems with different stochastic processes. Different from current TRA methods, POK-TRA regards the time parameter as a special interval variable, which converts TRA problem into a special hybrid reliability analysis (HRA) problem with one interval variable. Based on the concept of projection outline as well as a correlation condition, an efficient sampling strategy is proposed to refine the Kriging model adaptively. Secondly, POK-TRA is extended to the time-dependent reliability analysis including both random and interval variables (POK-iTRA). By inheriting the processing strategy of time parameter and stochastic processes, the iTRA problem is converted into the HRA problem with multiple interval variables. Finally, four cases are used to show the accuracy and efficiency of the proposed method.

Appendices

Kriging model

Kriging (Jones 2001; Sacks et al. 1989) is an interpolative metamodeling technique based on the assumption that the predicted function value is the linear combination of a regression model and a stochastic process. The general form of Kriging is given as

$$ \hat{y}\left(\mathbf{x}\right)={\mathbf{f}}^{\mathrm{T}}\left(\mathbf{x}\right)\beta +z\left(\mathbf{x}\right) $$

(A1)

where f(x) = [f₁(x), f₂(x), ..., f_p(x)]^T is a vector of regression functions and β = [β₁, β₂, ..., β_p]^T is the regression parameters vector. z(x) is a stochastic process with mean zero and variance σ². In this paper, the ordinary Kriging is used, which means that f^T(x)β is a scalar and always taken as f^T(x)β =  β. In other words, the function value obeys the normal distribution y(x) ∼ N(μ,  σ²), μ = β. The covariance of two random points is defined by

$$ Cov\left[z\left({\mathbf{x}}_i\right),z\left({\mathbf{x}}_j\right)\right]={\sigma}^2R\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\sigma}^2\exp \left[-\sum \limits_{l=1}^d{\uptheta}_l{\left({\mathbf{x}}_i^l-{\mathbf{x}}_j^l\right)}^2\right] $$

(A2)

where R(x_i, x_j) is the correlation function between z(x_i) and z(x_j) and the Gaussian correlation function is widely used for R(x_i, x_j). d is the number of design variables; ${\mathbf{x}}_i^l,{\mathbf{x}}_j^l\ \mathrm{and}\ {\uptheta}_l$ are the l − th component of x_i, x_j and θ, respectively.

Given a design of experiment (DOE) X = [x₁, x₂, ..., x_n] and their corresponding function value Y = [y₁, y₂, ..., y_n]^T, to evaluate the value of parameter θ, Kriging chooses μ and σ² to maximize the likelihood function of Y

$$ L\left({y}_1,{y}_2,...,{y}_n|\mu, {\sigma}^2\right)=\frac{1}{{\left(2\pi \right)}^{\frac{n}{2}}{\left({\sigma}^2\right)}^{\frac{n}{2}}{\left|\mathbf{R}\right|}^{\frac{1}{2}}}\exp \left[-\frac{{\left(\mathbf{Y}-\mathbf{1}\mu \right)}^{\mathrm{T}}{\mathbf{R}}^{-1}\left(\mathbf{Y}-\mathbf{1}\mu \right)}{2{\sigma}^2}\right] $$

(A3)

where R is an n × n correlation matrix R = [R(x_i, x_j)]_n × n and 1 is an n × 1 unit vector. Then setting the derivatives with respect to μ and σ² to zero and solving the maximum likelihood estimates (MLEs) are obtained by

$$ \hat{\mu}=\frac{{\mathbf{1}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{Y}}{{\mathbf{1}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{1}},{\hat{\sigma}}^2=\frac{{\left(\mathbf{Y}-\mathbf{1}\hat{\mu}\right)}^{\mathrm{T}}{\mathbf{R}}^{-1}\left(\mathbf{Y}-\mathbf{1}\hat{\mu}\right)}{n}. $$

(A4)

Substituting Eq. (A4) into Eq. (A3), the concentrated log-likelihood function is obtained. And ignoring the constant terms, the MLE for θ is given

$$ \hat{\theta}=\underset{\theta }{\mathrm{argmax}}\left(\frac{n}{2}\log \left({\hat{\sigma}}^2\right)-\frac{1}{2}\log \left(\left|\mathbf{R}\right|\right)\right). $$

(A5)

To make a prediction $\hat{y}$ at an unknown point x, defining a vector of correlations r(x) = [R(x, x₁), R(x, x₂), ..., R(x, x_n)]^T between the samples and the prediction point, an augmented correlation matrix and response vector can be constructed as

$$ \tilde{R}=\left(\begin{array}{cc}\mathbf{R}& \mathbf{r}\\ {}{\mathbf{r}}^{\mathrm{T}}& 1\end{array}\right),\tilde{\mathbf{y}}=\left(\begin{array}{c}\mathbf{Y}\\ {}\hat{y}\end{array}\right). $$

(A6)

Similarly, replacing R and Y in (A4) with $\tilde{R}$ and $\tilde{y}$, we can evaluate the MLEs

$$ {\mu}_{\hat{y}}\left(\mathbf{x}\right)=\hat{\mu}+{\mathbf{r}}^{\mathrm{T}}{\mathbf{R}}^{-1}\left(\mathbf{Y}-\mathbf{1}\hat{\mu}\right),{\hat{\sigma}}_{\hat{y}}^2\left(\mathbf{x}\right)={\hat{\sigma}}^2\left[1-{\mathbf{r}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{r}+\frac{{\left(1-{\mathbf{r}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{r}\right)}^2}{{\mathbf{1}}^{\mathrm{T}}{\mathbf{R}}^{-1}\mathbf{1}}\right]. $$

(A7)

Thus the predicted response at x obeys a normal distribution $\hat{y}\left(\mathbf{x}\right)\sim N\left({\mu}_{\hat{y}}\left(\mathbf{x}\right),{\hat{\sigma}}_{\hat{y}}^2\left(\mathbf{x}\right)\right)$. ${\mu}_{\hat{y}}\left(\mathbf{x}\right)$ is usually taken as the predicted response, and ${\hat{\sigma}}_{\hat{y}}^2\left(\mathbf{x}\right)$ means the local uncertainty of the prediction.

EOLE

Before building the Kriging model for the performance function, the stochastic process Y(t) can be represented by a series of independent random variables. In this work, the expansion optimal linear estimation (EOLE) method (Li and Der Kiureghian 1993) is utilized. The time interval is discretized into N_t time nodes, and the covariance function between any time ${t}_{t_i}$ and ${t}_{t_j}$ is computed by

$$ Cov\left({t}_{t_i},{t}_{t_j}\right)={\sigma}_Y\left({t}_{t_i}\right){\sigma}_Y\left({t}_{t_j}\right){\rho}_Y\left({t}_{t_i},{t}_{t_j}\right), $$

(B1)

where ${\rho}_Y\left({t}_{t_i},{t}_{t_j}\right)$ is the autocorrelation coefficient function. With the covariance function, the corresponding covariance matrix is formed as

$$ \sum =\left(\begin{array}{cccc} Cov\left({t}_{t_1},{t}_{t_1}\right)& Cov\left({t}_{t_1},{t}_{t_2}\right)& \dots & Cov\left({t}_{t_1},{t}_{t_{N_t}}\right)\\ {} Cov\left({t}_{t_2},{t}_{t_1}\right)& Cov\left({t}_{t_2},{t}_{t_2}\right)& \dots & Cov\left({t}_{t_2},{t}_{t_{N_t}}\right)\\ {}\vdots & \vdots & \ddots & \vdots \\ {} Cov\left({t}_{N_t},{t}_{t_1}\right)& Cov\left({t}_{N_1},{t}_{t_2}\right)& \dots & Cov\left({t}_{t_{N_t}},{t}_{t_{N_t}}\right)\end{array}\right). $$

(B2)

After the eigenanalysis of the covariance matrix, the stochastic process Y(t) is expanded by

$$ Y(t)={\mu}_Y(t)+\sum \limits_{m=1}^p\frac{1}{\sqrt{\lambda_m}}{\varPhi}_m(t){\xi}_m{\uprho}_Y(t), $$

(B3)

where p is the number of dominated eigenvalues and p ≤ N_t. λ_m is the eigenvalue, Φ_m(t) is the eigenvector, ${\uprho}_Y(t)={\left[{\sigma}_Y(t){\sigma}_Y\left({t}_{t_1}\right){\rho}_Y\left(t,{t}_{t_1}\right),{\sigma}_Y(t){\sigma}_Y\left({t}_{t_2}\right){\rho}_Y\left(t,{t}_{t_2}\right),...,{\sigma}_Y(t){\sigma}_Y\left({t}_{t_{N_t}}\right){\rho}_Y\left(t,{t}_{t_{N_t}}\right)\right]}^T$ is a vector of the covariance function, ξ_m is the independent standard normal variable. Figure 14 illustrates the expansion of two stochastic processes.

Fig. 14

Fifty realizations of stochastic process expansion