Efficient numerical simulation methods for estimating fuzzy failure probability based importance measure indices

Abstract

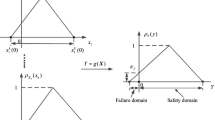
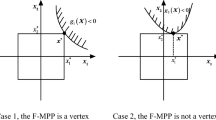
For the problem with a fuzzy failure state which commonly exists in degradation structures and systems, the fuzzy failure probability based importance measure indices can be used to measure the effect of the input variables on the fuzzy failure probability effectively. However, the computational cost is unaffordable for estimating the indices directly. For efficiently evaluating the fuzzy failure probability based importance measure indices, this paper proposed two numerical simulation methods, i.e., the direct Monte Carlo simulation method based on the Bayesian formula (B-DMCS) and the adaptive radial-based importance sampling method based on the Bayesian formula (B-ARBIS). The two proposed methods employ the Bayesian formula to eliminate the dependence of the computational cost on the dimensionality of the input variables. Compared with the B-DMCS method, the B-ARBIS method can enhance the computational efficiency significantly due to repeatedly utilizing the same group of samples of the input variables and the strategy to adaptively search the optimal hypersphere in the safety domain. After giving the principles and implementations of the two methods, three examples are employed to validate the effectiveness of the two proposed numerical simulation methods. The results of the examples demonstrate that the effectiveness of the two proposed methods is higher than the direct Monte Carlo method, and the B-ARBIS method can improve the efficiency obviously in contrast with the B-DMCS method.

Appendices

Appendix 1 Numerical scheme for the one-dimensional Gaussian quadrature

For λ ∈ [0, 1] can be seen as a uniform distribution, thus the Gauss-Legendre quadrature is adopted by this paper. The numerical quadrature formula of five-point Gauss-Legendre quadrature is shown in (32),

$$ {\int}_{\underset{\_}{\lambda}}^{\overline{\lambda}}f\left(\lambda \right) d\lambda \approx \frac{\overline{\lambda}-\underset{\_}{\lambda }}{2}\left[\sum \limits_{j=1}^5{w}_jf\left(\frac{\overline{\lambda}-\underset{\_}{\lambda }}{2}{\lambda}_j+\frac{\underset{\_}{\lambda }+\overline{\lambda}}{2}\right)\right] $$

(32)

where $\underset{\_}{\lambda }$ and $\overline{\lambda}$ are the lower bound and upper bound of λ, respectively. Obviously, in this paper, $\underset{\_}{\lambda }=0$ and $\overline{\lambda}=1$. f(λ) is the integrand related to λ, and in this paper, $f\left(\lambda \right)=P\left\{{F}_{\lambda}\right\}\left(1-\frac{f_{X_i}\left({x}_i|{F}_{\lambda}\right)}{f_{X_i}\left({x}_i\right)}\right)\kern0.1em$.

The Gaussian points λ_j(j = 1, 2, ⋯, 5) and the corresponding weights w_j(j = 1, 2, ⋯, 5) of five-point Gauss-Legendre quadrature are shown in Table 8.

Table 8 Gaussian points and weights of the five-point Gauss-Legendre quadrature

Appendix 2 The kernel density estimation method for estimating the probability density function

Kernel density estimation method has been proved to be an important tool in the statistical analysis of data. The univariate kernel density estimation is employed in this paper for estimating the conditional PDF ${f}_{X_i}\left({x}_i|{F}_{\lambda_j}\right)\left(i=1,2,\cdots, n\kern0.3em ;j=1,2,\cdots, k\right)$. Given M_j independent realizations ${\left({x}_{i1}^{(j)},{x}_{i2}^{(j)},\cdots, {x}_{i{M}_j}^{(j)}\right)}^T$ from an unknown continuous PDF ${f}_{X_i}\left({x}_i|{F}_{\lambda_j}\right)$, the basic KDE ${\hat{\delta}}_{X_i}\left({x}_i|{F}_{\lambda_j}\right)$ of ${f}_{X_i}\left({x}_i|{F}_{\lambda_j}\right)$ is defined as (33),

$$ {\hat{\delta}}_{X_i}\left({x}_i|{F}_{\lambda_j}\right)=\frac{1}{M_jh}\sum \limits_{s=1}^{M_j}K\left(\frac{x_i-{x}_{is}^{(j)}}{h}\right) $$

(33)

where K(⋅) is the kernel function, and h is the bandwidth which determines the smoothness of the model estimates. In this paper, the Gaussian kernel function is adopted, the bin width is specified by an improved plug-in bandwidth selection method, and the relevant Matlab code is available in Ref. (Cui et al. 2010).