Sensitivity of structural response in context of linear and non-linear buckling analysis with solid shell finite elements

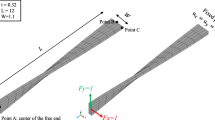
Abstract

The paper is concerned with the sensitivity analysis of structural responses in context of linear and non-linear stability phenomena like buckling and snapping. The structural analysis covering these stability phenomena is summarised. Design sensitivity information for a solid shell finite element is derived. The mixed formulation is based on the Hu-Washizu variational functional. Geometrical non-linearities are taken into account with linear elastic material behaviour. Sensitivities are derived analytically for responses of linear and non-linear buckling analysis with discrete finite element matrices. Numerical examples demonstrate the shape optimisation maximising the smallest eigenvalue of the linear buckling analysis and the directly computed critical load scales at bifurcation and limit points of non-linear buckling analysis, respectively. Analytically derived gradients are verified using the finite difference approach.

Appendices

Appendix: A: Structural analysis for solid shells

A brief summary of the element formulation presented by Klinkel et al. (2006) and Klinkel and Wagner (2008) for structural analysis is given. Additional sensitivity quantities by means of the pseudo load and sensitivity matrices presented by Gerzen et al. (2013) and (Gerzen 2014) are summarised as well. The shell continuum Ω _R is divided in element domains Ω _{R e} , which can be expressed with the assembly over all elements ${\Omega }_{R}=\overset {\text {nel}}{\underset {{e=1}}{{{ A}}}}{\Omega }_{Re}$. A low order hexahedral solid shell element is build. Isoparametric trilinear approximations of geometry and displacement field result in an eight node solid shell element with three displacement degrees of freedom per node. The superscript h indicates the field variables after discretisation. The subscript e indicates quantities on element level.

1.1 A.1 Approximation of kinematic quantities

Geometry, displacements and its variations are interpolated in the same manner

$$ \boldsymbol{X}^{h}=\boldsymbol{N} \hat{X}_{e},\quad\boldsymbol{u}^{h}=\boldsymbol{N} \hat{u}_{e}\quad\text{and}\quad\delta\boldsymbol{u}^{h}=\boldsymbol{N}\delta \hat{u}_{e}. $$

(96)

The discrete nodal coordinates, displacements and variations are arranged in the vectors $\hat {\boldsymbol {X}}_{e}\in \mathbb {R}^{24\times 1}$, $\hat {\boldsymbol {u}}_{e}\in \mathbb {R}^{24\times 1}$ and $\delta \hat {\boldsymbol {u}}_{e}\in \mathbb {R}^{24\times 1}$, respectively. The shape functions for the nodes I=1,2,...,8

$$ N_{I}=\frac{1}{8}(1+{\xi^{1}_{I}}\xi^{1})(1+{\xi^{2}_{I}}\xi^{2})(1+{\xi^{3}_{I}}\xi^{3}), $$

(97)

with −1≤ξ ⁱ≤+1 are organised in the interpolation matrix N=[N ₁,...,N ₈] with the submatrix N _I =diag[N _I ,N _I ,N _I ]. The Cartesian coefficients of the Green-Lagrangian strain tensor E are ordered in the vector E=[E ₁₁,E ₂₂,E ₃₃,2E ₁₂,2E ₁₃,2E ₂₃]^T in Voigt notation. The covariant basis vectors in discrete form are

$$ \boldsymbol{G}_{i}^{h}=\boldsymbol{N}_{,i} \hat{X}_{e},\qquad \boldsymbol{g}_{i}^{h}=\boldsymbol{N}_{,i}(\hat{X}_{e}+ \hat{u}_{e}), $$

(98)

with N _,i containing the derivatives of the shape functions with respect to the convective coordinates ξ ⁱ. The necessary derivatives of the shape functions with respect to the global coordinates

$$ \frac{\partial N_{I}}{\partial \boldsymbol{X}}=[\boldsymbol{G}_{1}^{h}\, \boldsymbol{G}_{2}^{h}\, \boldsymbol{G}_{3}^{h}]^{-T}\frac{\partial N_{I}}{\partial \boldsymbol \xi} $$

(99)

can be computed.

1.2 A.2 Approximation of strains and their variations.

The local convective strain components are approximated with

$$\begin{array}{@{}rcl@{}} &&\boldsymbol{E}^{h}_{L}=\\ &&\left[\begin{array}{c} \frac{1}{2}(g_{11}^{h}-G_{11}^{h})\\ \frac{1}{2}(g_{22}^{h}-G_{22}^{h})\\ \sum\limits_{L=i}^{iv}\frac{1}{4}(1+{\xi^{1}_{L}}\xi^{1})(1+{\xi^{2}_{L}}\xi^{2})\frac{1}{2}(g_{33}^{L}-G_{33}^{L})\\ (g_{12}^{h}-G_{12}^{h})\\ \frac{1}{2}((1-\xi^{2})(g_{13}^{B}-G_{13}^{B})+(1+\xi^{2})(g_{13}^{D}-G_{13}^{D}))\\ \frac{1}{2}((1-\xi^{1})(g_{23}^{A}-G_{23}^{A})+(1+\xi^{1})(g_{23}^{C}-G_{23}^{C})) \end{array}\right].\\ \end{array} $$

(100)

The corresponding strains are computed via ANS interpolation. A transformation to Cartesian coordinates

$$ \boldsymbol{E}^{h}=\boldsymbol{T}_{S}^{-T}\boldsymbol{E}^{h}_{L} $$

(101)

can be done using the transformation matrix $\boldsymbol {T}_{S}^{-T}$. It is defined via $\boldsymbol {T}_{S}=\boldsymbol {T}(\bar {a},\bar {b})$ with $\bar {a}=2$, $\bar {b}=1$ and

$$\begin{array}{@{}rcl@{}} &&\boldsymbol{T}=\left[\begin{array}{llll} (J_{11})^{2}&(J_{12})^{2}&(J_{13})^{2} &{\dots} \\ (J_{21})^{2}&(J_{22})^{2}&(J_{23})^{2} &{\dots} \\ (J_{31})^{2}&(J_{32})^{2}&(J_{33})^{2} &{\dots} \\ bJ_{11}J_{21}&bJ_{12}J_{22}&bJ_{13}J_{23}&\dots\\ bJ_{11}J_{31}&bJ_{12}J_{32}&bJ_{13}J_{33}&\dots\\ bJ_{21}J_{31}&bJ_{22}J_{32}&bJ_{23}J_{33}&\dots \end{array}\right.\\&& \left. \begin{array}{cccc} \dots&aJ_{11}J_{12}&aJ_{11}J_{13}&aJ_{12}J_{13} \\ \dots&aJ_{21}J_{22}&aJ_{21}J_{23}&aJ_{22}J_{23} \\ \dots&aJ_{31}J_{32}&aJ_{31}J_{33}&aJ_{32}J_{33} \\ \dots&J_{11}J_{22}+J_{12}J_{21}&J_{11}J_{23}+J_{13}J_{21}&J_{12}J_{23}+J_{13}J_{22}\\ \dots&J_{11}J_{32}+J_{12}J_{31}&J_{11}J_{33}+J_{13}J_{31}&J_{12}J_{33}+J_{13}J_{32}\\ \dots&J_{21}J_{32}+J_{22}J_{31}&J_{21}J_{33}+J_{23}J_{31}&J_{22}J_{33}+J_{23}J_{32} \end{array}\right].\\ \end{array} $$

(102)

and $J_{ik}=\boldsymbol {e}_{i}\cdot \boldsymbol {G}_{k}^{h}$. The vectors $\boldsymbol {G}_{k}^{h}$ are the well known convective tangent vectors and e _i are the orthogonal unit base vectors of Cartesian space. On element level the approximation of the virtual and incremental Green-Lagrangian strains reads

$$ \delta\boldsymbol{E}^{h}=\boldsymbol{B}\delta \hat{u}_{e},\qquad \Delta\boldsymbol{E}^{h}=\boldsymbol{B}\Delta \hat{u}_{e}, $$

(103)

respectively. For the approximation the interpolation matrix reads

$$ \boldsymbol{B}=\boldsymbol{T}_{S}^{-T}\boldsymbol{B}_{L}\qquad\text{with}\quad \boldsymbol{B}_{L}=[\boldsymbol{B}_{L1},...,\boldsymbol{B}_{L8}]. $$

(104)

The submatrix B _{L I} at I-th node is given by

$$ \boldsymbol{B}_{LI}=[\boldsymbol{B}_{LI}^{1},\boldsymbol{B}_{LI}^{2},\boldsymbol{B}_{LI}^{3},\boldsymbol{B}_{LI}^{4},\boldsymbol{B}_{LI}^{5},\boldsymbol{B}_{LI}^{6}]^{T} $$

(105)

with

$$\begin{array}{@{}rcl@{}} \boldsymbol{B}_{LI}^{1}&=&N_{I,1}(\boldsymbol{g}_{1}^{h})^{T},\\ \boldsymbol{B}_{LI}^{2}&=&N_{I,2}(\boldsymbol{g}_{2}^{h})^{T},\\ \boldsymbol{B}_{LI}^{3}&=&\sum\limits_{L=i}^{iv}\frac{1}{4}(1+{\xi^{1}_{L}}\xi^{1})(1+{\xi^{2}_{L}}\xi^{2})N_{I,3}^{L}(\boldsymbol{g}_{3}^{L})^{T},\\ \boldsymbol{B}_{LI}^{4}&=&N_{I,1}(\boldsymbol{g}_{2}^{h})^{T}+N_{I,2}(\boldsymbol{g}_{1}^{h})^{T},\\ \boldsymbol{B}_{LI}^{5}&=&\frac{1}{2}((1-\xi^{2})(N_{I,1}^{B}(\boldsymbol{g}_{3}^{B})^{T}+N_{I,3}^{B}(\boldsymbol{g}_{1}^{B})^{T})) \\&&+\frac{1}{2}((1+\xi^{2})(N_{I,1}^{D}(\boldsymbol{g}_{3}^{D})^{T}+N_{I,3}^{D}(\boldsymbol{g}_{1}^{D})^{T})),\\ \boldsymbol{B}_{LI}^{6}&=&\frac{1}{2}((1-\xi^{1})(N_{I,2}^{A}(\boldsymbol{g}_{3}^{A})^{T}+N_{I,3}^{A}(\boldsymbol{g}_{2}^{A})^{T})) \\&& +\frac{1}{2}((1+\xi^{1})(N_{I,2}^{C}(\boldsymbol{g}_{3}^{C})^{T}+N_{I,3}^{C}(\boldsymbol{g}_{2}^{C})^{T})). \end{array} $$

(106)

The superscripts A,B,C,D denote collocation points of assumed natural strain (ANS) interpolation for the treatment of transverse shear locking A=(−1,0,0), B=(0,−1,0), C=(1,0,0) and D=(0,1,0) in convective coordinates ξ ⁱ. To overcome curvature thickness locking the collocation points i=(−1,−1,0), i i=(1,−1,0), i i i=(1,1,0) and i v=(−1,1,0) in convective coordinates ξ ⁱ are chosen. They are denoted with superscript L = i,i i,i i i,i v. Details on how to choose these collocation points can be found in Klinkel et al. (2006) and references therein. Due to the ANS interpolations from now on the element formulation is not isotropic any more and ξ ³ denotes the thickness direction. The quantity $\Delta \delta \boldsymbol {E}:{\hat {\boldsymbol {S}}}$ from the linearisation of the weak form (120) is approximated in the following way The first quantity K _e is obtained by the discretisation of

$$ (\Delta\delta{\boldsymbol{E}}:{\hat{\boldsymbol{S}}})^{h}=\delta \hat{u}_{e}^{T}\boldsymbol{G}\Delta \hat{u}_{e},~ \boldsymbol{G}=\left[\begin{array}{ccc} \boldsymbol{G}_{11}&\cdots&\boldsymbol{G}_{18}\\ \vdots&\ddots&\vdots\\ \boldsymbol{G}_{81}&\cdots&\boldsymbol{G}_{88} \end{array}\right] $$

(107)

given by the submatrices G _{I J} =diag[G _{I J} ,G _{I J} ,G _{I J} ] for the node combination I, J defined by the scalar

$$ G_{IJ}=\left( \hat{S}^{h}\right)^{T}\boldsymbol{B}_{IJ}. $$

(108)

The required matrix B _{I J} is known from (35).

1.3 A.3 Approximation of assumed strain fields

The strain tensor ${\bar {\boldsymbol {E}}}$ is additively decomposed

$$ {\bar{\boldsymbol{E}}}=\hat{\boldsymbol{E}}+\tilde{\boldsymbol{E}}=\hat{E}^{ij}\boldsymbol{G}_{i}\otimes\boldsymbol{G}_{j}+\tilde{E}_{ij}\boldsymbol{G}^{i}\otimes\boldsymbol{G}^{j}. $$

(109)

The components of the strain fields $\hat {\boldsymbol {E}}$ and $\tilde {\boldsymbol {E}}$ are interpolated in local convective co-ordinates and transformed to Cartesian coordinates using Voigt Notation. The transformation of the contravariant components $\hat {E}^{ij}$ is done by the transformation matrix $\boldsymbol {T}_{E}=\boldsymbol {T}(\bar {a},\bar {b})$ with $\bar {a}=1$, $\bar {b}=2$, cf. (102). The approximation of the strain field in vector notation is

$$ \hat{E}^{h}=\boldsymbol{N}_{E}\boldsymbol \alpha_{e}^{1},\quad \boldsymbol \alpha_{e}^{1}\in\mathbb{R}^{18},\quad \boldsymbol{N}_{E}=\boldsymbol{T}_{E}^{0}\boldsymbol{N}_{L} $$

(110)

with

$$ \boldsymbol{N}_{L}=[\boldsymbol{I}\quad \hat{\boldsymbol{N}}\quad \hat{\hat{\boldsymbol{N}}}]. $$

(111)

Quantities evaluated at the centre of the element are denoted with the superscript 0. $\boldsymbol {I}\in \mathbb {R}^{6\times 6}$ is the identity matrix. The interpolation matrices in natural coordinates are

$$ \hat{\boldsymbol{N}}=\left[\begin{array}{lllll} \xi^{3}&\xi^{2}\xi^{3}&0&0&0\\ 0&0&\xi^{3}&\xi^{1}\xi^{3}&0\\ 0&0&0&0&0\\ 0&0&0&0&\xi^{3}\\ 0&0&0&0&0\\ 0&0&0&0&0 \end{array}\right] $$

(112)

and

$$ {\hat{\hat{\boldsymbol{N}}}}=\left[\begin{array}{lllllll} \xi^{2}&0&0&0&0&0&0\\ 0&\xi^{1}&0&0&0&0&0\\ 0&0&\xi^{1}&\xi^{2}&\xi^{1}\xi^{2}&0&0\\ 0&0&0&0&0&0&0\\ 0&0&0&0&0&\xi^{2}&0\\ 0&0&0&0&0&0&\xi^{1} \end{array}\right]. $$

(113)

Klinkel et al. (2006) call $\tilde {\boldsymbol {E}}$ the enhanced assumed strain field. Its covariant components are interpolated and transformed to Cartesian space using the relations

$$ \tilde{E}^{h}=\boldsymbol{M}_{E}\,\boldsymbol \alpha_{e}^{2},~ \boldsymbol \alpha_{e}^{2}\in\mathbb{R}^{7}~\text{with}~\boldsymbol{M}_{E}=\boldsymbol{T}_{M}\boldsymbol{M} $$

(114)

and

$$ \boldsymbol{T}_{M}=\frac{\det\boldsymbol{J}^{0}}{\det\boldsymbol{J}}(\boldsymbol{T}_{S}^{0})^{-T}. $$

(115)

$\boldsymbol {J}=[\boldsymbol {G}_{1}^{h},\boldsymbol {G}_{2}^{h},\boldsymbol {G}_{3}^{h}]^{T}$ is the Jacobian matrix. The interpolation matrix for the enhanced assumed strain field in natural coorinates reads

$$ \boldsymbol{M}=\left[\begin{array}{ccccccc} \xi^{1}&\xi^{1}\xi^{2}&0&0&0&0&0\\ 0&0&\xi^{2}&\xi^{1}\xi^{2}&0&0&0\\ 0&0&0&0&\xi^{3}&\xi^{1}\xi^{3}&\xi^{2}\xi^{3}\\ 0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0\\ 0&0&0&0&0&0&0 \end{array}\right]. $$

(116)

The interpolation of the total strain can now be expressed as

$$ \bar{E}^{h}=\boldsymbol{N}_{E}\boldsymbol \alpha_{e}^{1}+\boldsymbol{M}_{E}\boldsymbol \alpha_{e}^{2}. $$

(117)

Derivatives of strain energy function yield the 2nd Piola-Kirchhoff stresses and the material matrix

$$ \bar{S}^{h}=\frac{\partial W_{Re}}{\partial \bar{E}^{h}},\quad \bar{C}^{h}=\frac{\partial^{2} W_{Re}}{\partial \bar{E}^{h}\partial \bar{E}^{h}}, $$

(118)

respectively.

1.4 A.4 Approximation of assumed stress fiels

The interpolation of the stress field $\hat {S}^{h}$ reads

$$ \hat{S}^{h}=\boldsymbol{N}_{S}\boldsymbol \beta_{e},\quad \boldsymbol \beta_{e}\in\mathbb{R}^{18}\quad\text{with}\quad \boldsymbol{N}_{S}=\boldsymbol{T}_{S}^{0}\boldsymbol{N}_{L}. $$

(119)

The same procedure is used for the virtual stresses $\delta \hat {S}^{h}$ and the incremental stresses $\delta \hat {S}^{h}$. The transformation to global co-ordinates is done by the transformation matrix $\boldsymbol {T}_{S}^{0}=\boldsymbol {T}(\bar {a},\bar {b})$ with $\bar {a}=2$, $\bar {b}=1$. The superscript 0 denotes quantities evaluated at the element centre. The transformation matrix T is given by (102).

1.5 A.5 Element matrices and vectors

Element matrices are

$$\begin{array}{@{}rcl@{}} \boldsymbol{K}_{e}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{G}\,d{\Omega}_{e},\\ \boldsymbol{L}_{e}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{N}_{S}^{T}\boldsymbol{B}\,d{\Omega}_{e},\\ \boldsymbol{C}_{e}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{N}_{S}^{T}\boldsymbol{N}_{E}\,d{\Omega}_{e},\\ \boldsymbol{A}_{e}^{11}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{N}_{E}^{T} \bar{C}^{h}\boldsymbol{N}_{E}\,d{\Omega}_{e},\\ \boldsymbol{A}_{e}^{12}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{N}_{E}^{T} \bar{C}^{h}\boldsymbol{M}_{E}\,d{\Omega}_{e},\\ \boldsymbol{A}_{e}^{21}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{M}_{E}^{T} \bar{C}^{h}\boldsymbol{N}_{E}\,d{\Omega}_{e},\\ \boldsymbol{A}_{e}^{22}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{M}_{E}^{T} \bar{C}^{h}\boldsymbol{M}_{E}\,d{\Omega}_{e} \end{array} $$

(120)

and element vectors are

$$\begin{array}{@{}rcl@{}} \boldsymbol{f}_{e}^{\text{int}}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{B}^{T} \hat{\boldsymbol{S}}^{h}\,d{\Omega}_{e},\\ \boldsymbol{f}_{e}^{\text{ext}}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{N}^{T},d{\Omega}_{e}+\int\limits_{{{\Gamma}_{N}^{e}}}\boldsymbol{N}^{T}\boldsymbol{t}\,d{\Gamma}_{e},\\ \boldsymbol{a}_{e}^{1}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{N}_{E}^{T}\left( \bar{\boldsymbol{S}}^{h}- \hat{\boldsymbol{S}}^{h}\right)\,d{\Omega}_{e},\\ \boldsymbol{a}_{e}^{2}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{M}_{E}^{T} \bar{\boldsymbol{S}}^{h}\,d{\Omega}_{e},\\ \boldsymbol{b}_{e}&=&\int\limits_{{\Omega}_{Re}}\boldsymbol{N}_{S}^{T}\left( \boldsymbol{E}^{h}- \hat{\boldsymbol{E}}^{h}\right)\,d{\Omega}_{e}. \end{array} $$

(121)

Appendix: B: Sensitivity analysis for solid shells

Quantities for design sensitivity analysis by means of the pseudo load and sensitivity matrices derived by Gerzen et al. (2013) are summarised briefly.

1.1 B.1 Variational relations

For the computation of total derivatives of objectives and constraints after (43) pseudo load and sensitivity operator are desired. The pseudo load operator is obtained as variation of the physical residual with respect to the design

$$ p=\delta_{\text{{X}}}R_u+\delta_{\text{{X}}}R_{{{\hat{S}}}}+\delta_{\text{{X}}}R_{{{\bar{E}}}}= p_u+p_{{{\hat{S}}}}+p_{{{\bar{E}}}} $$

(122)

with the partial derivatives

$$\begin{array}{@{}rcl@{}} p_u(\boldsymbol{v},\boldsymbol{X};\delta\boldsymbol{u},\delta\boldsymbol{X})&=&\int\limits_{{\Omega}_{R}}\left( \delta_u\boldsymbol{E}: \hat{\boldsymbol{S}}-\delta\boldsymbol{u}\cdot\boldsymbol{b}\right)\,\text{Div}\delta\boldsymbol{X}\,d\Omega\\ &&+\int\limits_{{\Omega}_{R}}\left( \delta_{\text{{X}}}(\delta_u\boldsymbol{E}): \hat{\boldsymbol{S}}+\delta_u\boldsymbol{E}:\delta_{\text{{X}}}{ \hat{S}}\right)\,d\Omega,\\ p_{{{\hat{S}}}}(\boldsymbol{v},\boldsymbol{X};\delta \hat{S},\delta\boldsymbol{X})&=&\int\limits_{{\Omega}_{R}}\delta \hat{S}:\left( \boldsymbol{E}-\bar{\boldsymbol{E}}\right)\,\text{Div}\delta\boldsymbol{X}\,d\Omega\\ &&+\int\limits_{{\Omega}_{R}}\delta_{\text{{X}}}\left( \delta \hat{S}:\left( \boldsymbol{E}-\bar{\boldsymbol{E}}\right)\right)\,d\Omega,\\ p_{{{\bar{E}}}}(\boldsymbol{v},\boldsymbol{X};\delta\bar{E},\delta\boldsymbol{X})&=&\int\limits_{{\Omega}_{R}}\delta\bar{\boldsymbol{E}}:\left( \frac{\partial W_{R}}{\partial \bar{\boldsymbol{E}}}- \hat{\boldsymbol{S}}\right)\,\text{Div}\delta\boldsymbol{X}\,d\Omega\\ &&+\int\limits_{{\Omega}_{R}}\delta_{\text{{X}}}\left( \delta\bar{\boldsymbol{E}}:\left( \frac{\partial W_{R}}{\partial \bar{\boldsymbol{E}}}- \hat{S}\right)\right)\,d\Omega. \end{array} $$

(123)

1.2 B.2 Discretised relations

For the discretisation of the pseudo load matrix, derivatives of transformation matrices and strains as well as the approximation of a divergence are desired. The term Divδ X is approximated with

$$ (\text{Div}\delta\boldsymbol{X})^{h}=\boldsymbol{D}\delta \hat{\boldsymbol{X}}_{e} $$

(124)

and

$$ \boldsymbol{D}=[\boldsymbol{d}_{1},...,\boldsymbol{d}_{8}],\quad \boldsymbol{d}_{I}=[N_{I,1}\quad N_{I,2} \quad N_{I,3}]. $$

(125)

The derivative of the transformation matrix T from (102) with respect to $\hat {\boldsymbol {X}}_{e}$ is denoted with ${\mathbb {T}}\in \mathbb {R}^{6\times 6\times 24}$. Its coefficients are

$$\begin{array}{@{}rcl@{}} {\mathbb{T}}_{ijk_{1}(I)}&:=&H^{1}_{ij}(I), \quad k_{1}(I)=3I-2, \\ {\mathbb{T}}_{ijk_{2}(I)}&:=&H^{2}_{ij}(I), \quad k_{2}(I)=3I-1, \\ {\mathbb{T}}_{ijk_{3}(I)}&:=&H^{3}_{ij}(I), \quad k_{3}(I)=3I, \end{array} $$

(126)

with I=1,...,8 . Submatrices are

$$ \boldsymbol{H}^{1}(I)=\left[\boldsymbol{H}^{11}\;\boldsymbol{H}^{12}\right] $$

(127)

with

$$ \boldsymbol{H}^{11}=\left[\begin{array}{ccc} 2J_{11}N_{I,1}& 2J_{12}N_{I,2}& 2J_{13}N_{I,3}\\ 0& 0& 0\\ 0& 0& 0\\ J_{21}N_{I,1}b& J_{22}N_{I,2}b& J_{23}N_{I,3}b\\ J_{31}N_{I,1}b& J_{32}N_{I,2}b& J_{33}N_{I,3}b\\ 0& 0& 0 \end{array}\right] $$

(128)

and

$$ \boldsymbol{H}^{12}=\left[\begin{array}{lll} H^{12}_{11}& H^{12}_{12}& H^{12}_{13}\\ 0& 0& 0\\ 0& 0& 0\\ H^{42}_{41}& H^{12}_{42}& H^{12}_{43}\\ H^{52}_{51}& H^{12}_{52}& H^{12}_{53}\\ 0& 0& 0 \end{array}\right] $$

(129)

including

$$\begin{array}{@{}rcl@{}} H^{12}_{11}&=&J_{11}N_{I,2}a + J_{12}N_{I,1}a,\\ H^{12}_{12}&=&J_{11}N_{I,3}a + J_{13}N_{I,1}a,\\ H^{12}_{13}&=&J_{12}N_{I,3}a + J_{13}N_{I,2}a,\\ H^{12}_{41}&=&J_{21}N_{I,2} + J_{22}N_{I,1},\\ H^{12}_{42}&=&J_{21}N_{I,3} + J_{23}N_{I,1},\\ H^{12}_{43}&=&J_{22}N_{I,3} + J_{23}N_{I,2},\\ H^{12}_{51}&=&J_{31}N_{I,2} + J_{32}N_{I,1},\\ H^{12}_{52}&=&J_{31}N_{I,3} + J_{33}N_{I,1},\\ H^{12}_{63}&=&J_{32}N_{I,3} + J_{33}N_{I,2}, \end{array} $$

(130)

$$ \boldsymbol{H}^{2}(I)=\left[\boldsymbol{H}^{21}\;\boldsymbol{H}^{22}\right] $$

(131)

with

$$ \boldsymbol{H}^{21}=\left[\begin{array}{ccc} 0& 0& 0\\ 2J_{21}N_{I,1}& 2J_{22}N_{I,2}& 2J_{23}N_{I,3}\\ 0& 0& 0\\ J_{11}N_{I,1}b& J_{12}N_{I,2}b& J_{13}N_{I,3}b\\ 0& 0& 0\\ J_{31}N_{I,1}b& J_{32}N_{I,2}b& J_{33}N_{I,3}b \end{array}\right] $$

(132)

and

$$ \boldsymbol{H}^{22}=\left[\begin{array}{ccc} 0& 0& 0\\ H^{22}_{21}& H^{22}_{22}& H^{22}_{23}\\ 0& 0& 0\\ H^{22}_{41}& H^{22}_{42}& H^{22}_{43}\\ 0& 0& 0\\ H^{22}_{61}& H^{22}_{62}& H^{22}_{63} \end{array}\right] $$

(133)

including

$$\begin{array}{@{}rcl@{}} H^{22}_{21}&=&J_{21}N_{I,2}a + J_{22}N_{I,1}a,\\ H^{22}_{22}&=&J_{21}N_{I,3}a + J_{23}N_{I,1}a,\\ H^{22}_{23}&=&J_{22}N_{I,3}a + J_{23}N_{I,2}a,\\ H^{22}_{41}&=&J_{11}N_{I,2} + J_{12}N_{I,1},\\ H^{22}_{42}&=&J_{11}N_{I,3} + J_{13}N_{I,1},\\ H^{22}_{43}&=&J_{12}N_{I,3} + J_{13}N_{I,2},\\ H^{22}_{61}&=&J_{31}N_{I,2} + J_{32}N_{I,1},\\ H^{22}_{62}&=&J_{31}N_{I,3} + J_{33}N_{I,1},\\ H^{22}_{63}&=&J_{32}N_{I,3} + J_{33}N_{I,2}, \end{array} $$

(134)

and finally

$$ \boldsymbol{H}^{3}(I)=\left[\boldsymbol{H}^{31}\;\boldsymbol{H}^{32}\right] $$

(135)

with

$$ \boldsymbol{H}^{31}=\left[\begin{array}{ccc} 0& 0& 0\\ 0& 0& 0\\ 2J_{31}N_{I,1}& 2J_{32}N_{I,2}& 2J_{33}N_{I,3}\\ 0& 0& 0\\ J_{11}N_{I,1}b& J_{12}N_{I,2}b& J_{13}N_{I,3}b\\ J_{21}N_{I,1}b& J_{22}N_{I,2}b& J_{23}N_{I,3}b \end{array}\right] $$

(136)

and

$$ \boldsymbol{H}^{32}=\left[\begin{array}{ccc} 0& 0& 0\\ 0& 0& 0\\ H^{32}_{31}& H^{32}_{32}& H^{32}_{33}\\ 0& 0& 0\\ H^{32}_{51}& H^{32}_{52}& H^{32}_{53}\\ H^{32}_{61}& H^{32}_{62}& H^{32}_{63} \end{array}\right] $$

(137)

including

$$\begin{array}{@{}rcl@{}} H^{32}_{31}&=&J_{31}N_{I,2}a + J_{32}N_{I,1}a,\\ H^{32}_{32}&=&J_{31}N_{I,3}a + J_{33}N_{I,1}a,\\ H^{32}_{33}&=&J_{32}N_{I,3}a + J_{33}N_{I,2}a,\\ H^{32}_{51}&=&J_{11}N_{I,2} + J_{12}N_{I,1},\\ H^{32}_{52}&=&J_{11}N_{I,3} + J_{13}N_{I,1},\\ H^{32}_{53}&=&J_{12}N_{I,3} + J_{13}N_{I,2},\\ H^{32}_{61}&=&J_{21}N_{I,2} + J_{22}N_{I,1},\\ H^{32}_{62}&=&J_{21}N_{I,3} + J_{23}N_{I,1},\\ H^{32}_{63}&=&J_{22}N_{I,3} + J_{23}N_{I,2}. \end{array} $$

(138)

The transposed ${\mathbb {T}}^{T}$ is defined as ${\mathbb {T}}^{T}_{ijk}={\mathbb {T}}_{jik}$. The derivatives of applied transformation matrices read for the stresses ${\mathbb {T}}_{S}={\mathbb {T}}(\bar {a},\bar {b})$ with $\bar {a}=2$, $\bar {b}=1$ and for strains ${\mathbb {T}}_{E}={\mathbb {T}}(\bar {a},\bar {b})$ with $\bar {a}=1$, $\bar {b}=2$. Note that the notation means $T_{ij,\hat {X}_{k}}={\mathbb {T}}_{ijk}$. The derivative of the transformation matrix T _M with respect to $\hat {\boldsymbol {X}}_{e}$ is ${\mathbb {T}}_{M}\in \mathbb {R}^{6\times 6\times 24}$. With $(T_{M})_{ij,\hat {X}_{k}}=({\mathbb {T}}_{M})_{ijk}$ the derivative $(\boldsymbol {T}_{M})_{,\hat {X}_{k}}$ can be computed with J=[G ₁ G ₂ G ₃] and $\boldsymbol {J}^{0}=[\boldsymbol {G}_{1}^{0} \boldsymbol {G}_{2}^{0} \boldsymbol {G}_{3}^{0}]$ resulting in

$$\begin{array}{@{}rcl@{}} (\boldsymbol{T}_{M})_{,\hat{X}_{k}}&=&\left( \bigg((\boldsymbol{J}^{0})^{-T}:\boldsymbol{J}^{0}_{,\hat{X}_{k}}-\boldsymbol{J}^{-T}:\boldsymbol{J}_{,\hat{X}_{k}}\bigg)(\boldsymbol{T}_{S}^{0})^{-T}\right.\\ &&\left.-(\boldsymbol{T}_{S}^{0})^{-T}(\boldsymbol{T}_{S}^{0})^{T}_{,\hat{X}_{k}}(\boldsymbol{T}_{S}^{0})^{-T}\right)\frac{\left|\boldsymbol{J}^{0}\right|}{\left|\boldsymbol{J}\right|}. \end{array} $$

(139)

The scalar product (⋅:⋅) is applied to matrices, as it is defined for tensors. The computation of $\boldsymbol {J}^{0}_{,\hat {X}_{k}}$ and $\boldsymbol {J}_{,\hat {X}_{k}}$ is straightforward, details are omitted here. The first derivative of local strains $\boldsymbol {E}^{h}_{L}$ with respect to $\hat {X}_{e}$ is $(\boldsymbol {E}^{h}_{L})_{,\hat {X}}=\boldsymbol {Q}=[\boldsymbol {Q}_{1},...,\boldsymbol {Q}_{8}]$ with

$$ \boldsymbol{Q}_{I}=[\boldsymbol{Q}_{I1},\boldsymbol{Q}_{I2},\boldsymbol{Q}_{I3},\boldsymbol{Q}_{I4},\boldsymbol{Q}_{I5},\boldsymbol{Q}_{I6}]^{T} $$

(140)

and

$$\begin{array}{@{}rcl@{}} \boldsymbol{Q}_{I1}&=&N_{I,1}(\boldsymbol{u}_{,1}^{h})^{T},\\ \boldsymbol{Q}_{I2}&=&N_{I,2}(\boldsymbol{u}_{,2}^{h})^{T},\\ \boldsymbol{Q}_{I3}&=&\sum\limits_{L=i}^{iv}\frac{1}{4}(1+{\xi^{1}_{L}}\xi^{1})(1+{\xi^{2}_{L}}\xi^{2})N_{I,3}^{L}(\boldsymbol{u}_{,3}^{L})^{T}\\ \boldsymbol{Q}_{I4}&=&N_{I,1}(\boldsymbol{u}_{,2}^{h})^{T}+N_{I,2}(\boldsymbol{u}_{,1}^{h})^{T},\\ \boldsymbol{Q}_{I5}&=&\frac{1}{2}\left( (1-\xi^{2})(N_{I,1}^{B}(\boldsymbol{u}_{,3}^{B})^{T}+N_{I,3}^{B}(\boldsymbol{u}_{,1}^{B})^{T})\right.\\ &&+(1+\xi^{2})\left( N_{I,1}^{D}(\boldsymbol{u}_{,3}^{D})^{T}+N_{I,3}^{D}(\boldsymbol{u}_{,1}^{D})^{T}\right),\\ \boldsymbol{Q}_{I6}&=&\frac{1}{2}\left( (1-\xi^{1})(N_{I,2}^{A}(\boldsymbol{u}_{,3}^{A})^{T}+N_{I,3}^{A}(\boldsymbol{u}_{,2}^{A})^{T})\right.\\ &&\left.+(1+\xi^{1})(N_{I,2}^{C}(\boldsymbol{u}_{,3}^{C})^{T}+N_{I,3}^{C}(\boldsymbol{u}_{,2}^{C})^{T})\right) . \end{array} $$

(141)

1.3 B.3 Sensitivity and pseudo load matrices

The parts of the pseudo load are approximated as

$$\begin{array}{@{}rcl@{}} p_u^{h}=\delta \hat{u}_{e}\boldsymbol{P}_{u}^{e}\delta \hat{X}_{e},\quad p_{{\hat{S}}}^{h}=\delta \hat{S}^{h}\boldsymbol{P}_{{\hat{S}}}^e\delta \hat{X}_{e},\\ p_{{\bar{E}}}^{h}=\delta \hat{E}^{h}\boldsymbol{P}_{{\hat{E}}}^e\delta \hat{X}_{e}+\delta \tilde{E}^{h}\boldsymbol{P}_{{\tilde{E}}}^e\delta \hat{X}_{e} \end{array} $$

(142)

with matrices

$$\begin{array}{@{}rcl@{}} \boldsymbol{P}_{u}^{e}&=\int\limits_{{\Omega}_{R_{e}}}\left( \boldsymbol{B}^{T} \hat{\boldsymbol{S}}^{h}-\boldsymbol{N}^{T}\boldsymbol{b}\right)\boldsymbol{D}\,d{\Omega}_{e}\\ &+\int\limits_{{\Omega}_{R_{e}}}\boldsymbol{G}+\mathcal{P}\left( \boldsymbol{B}^{T},\,{\mathbb{T}}_{S}^{0},\, \boldsymbol{N}_{L}\boldsymbol \beta_{e}\right)\,d{\Omega}_{e}\\&-\int\limits_{{\Omega}_{R_{e}}}\mathcal{P}\left( \boldsymbol{B}_{L}^{T}\boldsymbol{T}_{S}^{-1},\,{\mathbb{T}}_{S},\,\boldsymbol{T}_{S}^{-1} \hat{\boldsymbol{S}}^{h}\right)\,d{\Omega}_{e}, \end{array} $$

(143)

$$\begin{array}{@{}rcl@{}} \boldsymbol{P}_{{\hat{S}}}^e&=&\int\limits_{{\Omega}_{R_{e}}}\left( \boldsymbol{N}_{S}^{T}(\boldsymbol{E}^{h}- \hat{\boldsymbol{E}}^{h})\right)\boldsymbol{D}\,d{\Omega}_{e}\\ &&+\int\limits_{{\Omega}_{R_{e}}}\mathcal{P}\left( \boldsymbol{N}_{L}^{T},\,({\mathbb{T}}_{S}^{0})^{T},\,(\boldsymbol{E}^{h}- \hat{\boldsymbol{E}}^{h})\right)\,d{\Omega}_{e}\\&&-\int\limits_{{\Omega}_{R_{e}}}\mathcal{P}\left( \boldsymbol{N}_{S}^{T},\,{\mathbb{T}}_{E}^{0},\,\boldsymbol{N}_{L}\boldsymbol \alpha_{e}^{1}\right)\,d{\Omega}_{e}\\ &&+\int\limits_{{\Omega}_{R_{e}}}\boldsymbol{N}_{S}^{T}\boldsymbol{T}_{S}^{-T}\boldsymbol{Q}\,d{\Omega}_{e}\\&&-\int\limits_{{\Omega}_{R_{e}}}\mathcal{P}\left( \boldsymbol{N}_{S}^{T}\boldsymbol{T}_{S}^{-T},\,{\mathbb{T}}_{S}^{T},\,\boldsymbol{T}_{S}^{-T}\boldsymbol{E}^{h}_{L}\right)\,d{\Omega}_{e}, \end{array} $$

(144)

$$ \begin{array}{ll} \boldsymbol{P}_{{\hat{E}}}^e&=\int\limits_{{\Omega}_{R_{e}}}\left( \boldsymbol{N}_{E}^{T}(\bar{\boldsymbol{S}}^{h}- \hat{\boldsymbol{S}}^{h})\right)\boldsymbol{D}\,d{\Omega}_{e}\\ &+\int\limits_{{\Omega}_{R_{e}}}\mathcal{P}\left( \boldsymbol{N}_{L}^{T},\,({\mathbb{T}}_{E}^{0})^{T},\,(\bar{\boldsymbol{S}}^{h}- \hat{\boldsymbol{S}}^{h})\right)\,d{\Omega}_{e}\\&+\int\limits_{{\Omega}_{R_{e}}}\mathcal{P}\left( \boldsymbol{N}_{E}^{T} \bar{C},\,{\mathbb{T}}_{E}^{0},\,\boldsymbol{N}_{L}\boldsymbol \alpha_{e}^{1}\right)\,d{\Omega}_{e}\\ &+\int\limits_{{\Omega}_{R_{e}}}\mathcal{P}\left( \boldsymbol{N}_{E}^{T} \bar{C},\,{\mathbb{T}}_{M},\,\boldsymbol{M}\boldsymbol \alpha_{e}^{2}\right)\,d{\Omega}_{e}\\&-\int\limits_{{\Omega}_{R_{e}}}\mathcal{P}\left( \boldsymbol{N}_{E}^{T},\,{\mathbb{T}}_{S}^{0},\,\boldsymbol{N}_{L}\boldsymbol \beta_{e}\right)\,d{\Omega}_{e} \end{array} $$

(145)

and

$$ \begin{array}{ll} \boldsymbol{P}_{{\tilde{E}}}^{e}&=\int\limits_{{\Omega}_{R_{e}}}\left( \boldsymbol{M}_{E}^{T} \bar{S}^{h}\right)\boldsymbol{D}\,d{\Omega}_{e}\\&+\int\limits_{{\Omega}_{R_{e}}}\left( \mathcal{P}\left( \boldsymbol{M}^{T},\,{\mathbb{T}}_{M}^{T},\, \bar{S}^{h}\right)\right)\,d{\Omega}_{e}\\ &+\int\limits_{{\Omega}_{R_{e}}}\mathcal{P}\left( \boldsymbol{M}_{E}^{T} \bar{C},\,{\mathbb{T}}_{E}^{0},\,\boldsymbol{N}_{L}\boldsymbol \alpha_{e}^{1}\right)\,d{\Omega}_{e}\\&+\int\limits_{{\Omega}_{R_{e}}}\mathcal{P}\left( \boldsymbol{M}_{E}^{T} \bar{C},\,{\mathbb{T}}_{M},\,\boldsymbol{M}\boldsymbol \alpha_{e}^{2}\right)\,d{\Omega}_{e}. \end{array} $$

(146)

The pseudo load and sensitivity matrices P _v and S _v are obtained by assembly over all finite elements of

$$ \boldsymbol{P}_{v}=\overset{\text{nel}}{\underset{{e=1}}{{{ A}}}}\boldsymbol{P}_{e}, \quad \boldsymbol{S}_{v}=\overset{\text{nel}}{\underset{{e=1}}{{{ A}}}}\boldsymbol{S}_{e} $$

(147)

of the element quantities

$$ \boldsymbol{P}_{e}=\left[\begin{array}{l}\boldsymbol{P}_{u}^{e}\\ \boldsymbol{P}_{{\hat{E}}}^e \\ \boldsymbol{P}_{{\tilde{E}}}^e \\ \boldsymbol{P}_{{\hat{S}}}^e \end{array}\right], \boldsymbol{S}_{e}=\left[\begin{array}{l}\boldsymbol{S}_{u}^{e}\\ \boldsymbol{S}_{{\hat{E}}}^e \\ \boldsymbol{S}_{{\tilde{E}}}^e \\ \boldsymbol{S}_{{\hat{S}}}^e \end{array}\right]. $$

(148)

respectively. To compute the sensitivity matrix their relation

$$ \boldsymbol{P}_{v}=-\boldsymbol{K}_{v}\boldsymbol{S}_{v}. $$

(149)

is used. Static condensation yields

$$ \boldsymbol{P}_{u}=-\boldsymbol{K}_{u}\boldsymbol{S}_{u} $$

(150)

with

$$ \boldsymbol{P}_{u}=\overset{\text{nel}}{\underset{{e=1}}{{{ A}}}}\boldsymbol{P}_{u_{e}} $$

(151)

and the element quantity

$$ \boldsymbol{P}_{u_{e}}=\boldsymbol{P}_{u}^{e}+\boldsymbol{L}_{e}^{T}\boldsymbol{C}_{e}^{-T}\boldsymbol{A}_{e}\boldsymbol{C}_{e}^{-1}\boldsymbol{P}_{{\hat{S}}}^e+\boldsymbol{L}_{e}^{T}\boldsymbol{C}_{e}^{-1}\boldsymbol{P}_{{E}}^e $$

(152)

using the abbreviation $\boldsymbol {P}_{{E}}^e=\boldsymbol {P}_{{\hat {E}}}^{e}-\boldsymbol {A}_{e}^{12}(\boldsymbol {A}_{e}^{22})^{-1}\boldsymbol {P}_{{\tilde {E}}}^e$. After solving the unknown displacement sensitivities, the sensitivities of stresses and strains can be calculated on element level as follows

$$ \begin{array}{ll} \boldsymbol{S}_{{\hat{E}}}^e&=\boldsymbol{C}_{e}^{-1}(\boldsymbol{L}_{e}\boldsymbol{S}_{u}^{e}+\boldsymbol{P}_{{\hat{S}}}^e),\\ \boldsymbol{S}_{{\tilde{E}}}^e&=-(\boldsymbol{A}_{e}^{22})^{-1}(\boldsymbol{P}_{{\tilde{E}}}^e+\boldsymbol{A}_{e}^{21}\boldsymbol{S}_{{\hat{E}}}^e),\\ \boldsymbol{S}_{{\hat{S}}}^e&=\boldsymbol{C}_{e}^{-T}(\boldsymbol{A}_{e}\boldsymbol{S}_{{\hat{E}}}^e+\boldsymbol{P}_{{E}}^{e}). \end{array} $$

(153)