Abstract
The performance of the sequential metamodel based optimization procedure depends strongly on the chosen building blocks for the algorithm, such as the used metamodeling method and sequential improvement criterion. In this study, the effect of these choices on the efficiency of the robust optimization procedure is investigated. A novel sequential improvement criterion for robust optimization is proposed, as well as an improved implementation of radial basis function interpolation suitable for sequential optimization. The leave-one-out cross-validation measure is used to estimate the uncertainty of the radial basis function metamodel. The metamodeling methods and sequential improvement criteria are compared, based on a test with Gaussian random fields as well as on the optimization of a strip bending process with five design variables and two noise variables. For this process, better results are obtained in the runs with the novel sequential improvement criterion as well as with the novel radial basis function implementation, compared to the runs with conventional sequential improvement criteria and kriging interpolation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Engineering can be seen as a sequence of making choices, from fundamental design choices to defining design details. In the last century, many empirical and theoretical models have been developed to help with these decisions. Nowadays engineers frequently use computational models to assess the effects of design choices and determine optimal designs.
In many engineering problems, it is infeasible to find an optimal design through trial and error due to a large number of interacting parameters. Therefore, many optimization methods have been developed to automate this process, each method being suitable to solve a specific type of problem in an efficient way. With these methods an optimal configuration of the design may be found. However, such a design may malfunction in real-life due to variability of the model parameters. A specific branch of optimization research focuses on these problems: within robust optimization the goal is to find a design which fulfills the requirements even under the influence of parameter variations.
When dealing with expensive computational models, it is desired to acquire insight into the problem at hand without performing an excessive amount of model evaluations. One approach is to replace the model with an easy to evaluate metamodel, also known as surrogate or response surface model. The metamodel is built based on a moderate number of evaluations of the computational model, and thereafter used for optimization. Some researchers developed methods to iteratively enrich the metamodels with new evaluations of the computational model. This is known as sequential optimization or sequential improvement.
Within this research the computational efficiency of sequential metamodel based robust optimization with expensive computational models is studied. The optimization flowchart is shown in Fig. 1. Robust optimization, metamodeling and sequential improvement have been combined in several studies, such as for the designs of an ordering policy of an inventory system (Huang et al. 2006), a loaded framework (Jurecka et al. 2007) and an industrial V-bending process (Wiebenga et al. 2012), as well as for the optimization of the crashworthiness of a foam-filled thin-walled structure (Sun et al. 2014), the blankholder force trajectory for springback reduction of an U-shaped high strength steel strip (Kitayama and Yamazaki 2014) and many mathematical benchmark problems (Huang et al. 2006; Wiebenga et al. 2012; Marzat et al. 2013; Janusevskis and Le Riche 2013; Ur Rehman et al. 2014).
The robust optimization procedure consists of several steps (Fig. 1). For some steps a choice has to be made between different methods to perform a prescribed task. For example, latin hypercube sampling, fractional factorial sampling, random sampling or a combination of these may be chosen as sampling strategy for the initial Design Of Experiments (DOE). To fit a set of data points, many methods have been developed, such as polynomial regression, neural networks, kriging, Radial Basis Functions (RBF), moving least squares and many others. Even within these methods many choices can be made on the exact configuration of the method. Hence, these methods can be seen as building blocks of the optimization algorithm. Every building block may be replaced with any other building block which is capable of performing the prescribed task. Clearly, the choice for a certain building block may severely affect the efficiency of the optimization algorithm.
In the present work, the efficiency of the robust optimization algorithm is studied. More specifically, the effects of the metamodeling method and the sequential improvement criterion on the optimization are examined. A widely used metamodeling method is kriging, as observed by several researchers (Wang and Shan 2007; Kleijnen 2009; Forrester and Keane 2009). One advantage of kriging is that it includes a prediction of the metamodel uncertainty. However, clustering of DOE points adversely affects the predictive capability of kriging methods (Zimmerman et al. 1999; Havinga et al. 2013). This is of interest because point clusters are formed during optimization due to the sequential improvement procedure. An interpolating metamodeling method which may be adapted to account for clustering of DOE points is RBF interpolation. Good fitting capabilities for nonlinear functions have been reported for RBF interpolation in several studies (Franke 1982; Jin et al. 2001). However, the uncertainty measures which have been developed for RBF are not suitable for sequential optimization. Therefore, an improved configuration of the RBF metamodel is proposed, taking into account the local DOE density and including a prediction of the metamodel uncertainty based on the Leave-One-Out Cross-Validation (LOOCV) measure.
Sequential improvement in robust optimization has been scarcely investigated up to now. For deterministic optimization, the Expected Improvement (EI) criterion was proposed by Jones et al. (1998). This criterion can be used for robust optimization, but does not take into account the uncertainty of the objective function value at the sampled design points. Jurecka (2007) adapted the expected improvement criterion of Jones for robust optimization. However, this criterion has some disadvantages which will be shown in this work. Therefore, a new expected improvement criterion for robust optimization is proposed.
The sequential robust optimization procedure is generic and, therefore, not limited to specific research fields. However, our interest goes to robust optimization of metal forming processes. The aim is to design metal forming processes with a low sensitivity to variations of material properties and process parameters such as friction and tool wear. Our background may be noticed in the examples given throughout this work, without violating the genericity of the approach.
This paper is structured as follows: in Section 2 a selective overview of the state of the art of robust optimization is given: the metamodeling methods including error prediction (Section 2.1) and the sequential improvement criterion (Section 2.2) are discussed. The RBF metamodel with uncertainty measure is proposed in Section 3. The novel robust expected improvement formulation is introduced in Section 4. The efficiency of the expected improvement criteria and metamodeling methods are compared in Section 5 based on mathematical functions. In Section 6 a demonstration problem is presented: a V-bending process with two noise variables, five design variables and two nonlinear constraints. The robust optimization results are given in Section 7 and the conclusion is given in Section 8.
2 State of the art in robust optimization
The famous paper of Jones et al. (1998) in which the expected improvement criterion was introduced, is titled Efficient Global Optimization of Expensive Black-Box Functions. The term black-box function denotes that it is not of interest how the function works. The only requirement is that the function is able to process a set of input variables and return one or multiple output values. Therefore, the optimization procedure is suitable for optimization with any kind of numerical model. Unlike experiments, trials with the same input variable values always give the same output value. Therefore, there is no need to perform multiple tests of the same variable set. The adjective expensive emphasizes the computational cost of the function and stresses the need to keep the number of function evaluations as low as possible.
In the case of deterministic optimization, both the black-box function as well as the optimization problem are defined in the design variable space x. In contrary, in robust optimization the black-box function is defined in the combined space of the design variable x and the noise variable z, while the optimization problem is stated in the design variable space x. At a certain point in the design space x ′, the objective function is defined by the behavior of the black-box function throughout subspace (x ′, z). Given an assumption on the probability distribution of the noise variable z, the probability distribution for the output of the black-box function may be determined at x ′, and subsequently this probability is used in the objective function.
Mathematically, the robust optimization problem can be stated as follows. As mentioned above, the black-box function f is a function of the design variable x and the noise variable z:
The noise variable z is a realization of the random variable Z with probability p Z (z):
Therefore, the random variable Y(x) is defined by f(x, z) and p Z (z):
The same holds for the inequality constraint functions g i (x, z) and the equality constraint functions h i (x, z). Hence, the general form of a robust optimization problem can be stated as follows:
The objective function Obj(Y(x)) determines which property of the probability distribution Y(x) should be minimized. The robustness of a production process can be defined in several ways, such as the average error of the production process or the percentage of the products that meet the product requirements. The most straightforward way to quantify these measures is to determine the statistical parameters of the process output Y(x), such as the mean μ Y , standard deviation σ Y or median. Two different ways to improve the accuracy of the process are by shifting the mean μ Y or decreasing the standard deviation σ Y (Koch et al. 2004). In some cases, these may be conflicting objectives (Beyer and Sendhoff 2007). Some researchers choose to combine these measures in a single objective, for example by minimizing μ Y + kσ Y , as is done in this study. Many other robust optimization objectives can be found in literature, such as Pareto front determination (Coelho and Bouillard 2011; Nishida et al. 2013), quantile optimization (Rhein et al. 2014), minimization of the worst case scenario (Marzat et al. 2013) and minimization of the signal-to-noise ratio (Taguchi and Phadke 1984; Leon et al. 1987).
The lower bound and upper bound of the design variables x are defined by L B and U B. The constraint functions C i (G i (x)) and \(\text {C}_{i}^{\text {eq}} (H_{i} (\mathbf {x} ) )\) determine the constraints for the distributions G i (x) and H i (x).
Usually, every simulation yields the values of the functions f, g i and h i for one variable set (x, z). However, the whole subspace (x, Z) must be known to exactly evaluate the objective function Obj(Y(x)) and the constraint functions C i (G i (x)) and \(\text {C}_{i}^{\text {eq}} (H_{i} (\mathbf {x} ) )\) for one value of the design variable x. Clearly, it is not desired to spend too many simulations for just one point in the design variable space. Therefore, the optimization algorithm should be able to handle uncertainty in the objective and constraint function values, and efficiently select whether to sample multiple points in the noise space or explore other regions of the design space.
When defining a robust optimization problem, one of the first problems is to determine the distribution p Z (z) of the noise variable z. In the optimization of a production process, these may be properties such as material variation, friction variation or sheet thickness variation. These variations can be characterized by min-max values or by statistical properties such as mean and standard deviation. In some cases, knowledge of the correlations between the different noise variables is required for a correct estimation of the robustness of the process (Wiebenga et al. 2014).
In the following sections the different components used to solve the optimization problem of (6) are discussed (see Fig. 1).
2.1 Metamodeling methods
A major component of the optimization algorithm is the metamodeling method which is used to fit the objective function f and the constraint functions g i and h i using a set of observations D = {(x (i), y (i))|i = 1…n}. The sequential improvement strategies discussed in this study (Section 2.2) do not only need the estimate of the functions \(\hat {f}\), \(\hat {g}_{i}\) and \(\hat {h}_{i}\) at untried points x but also require an estimate of the prediction uncertainty at these points. Therefore, only methods that provide this estimate will be discussed.
As a basis for interpolating simulation data, it is good practice to normalize the inputs and to use a regression model as underlying model. Often, a simple polynomial model is used to capture the major trends of the observations y. Hence, the metamodeling methods are used to fit the residue \(\mathbf {y} - \hat {f}_{\text {regr}}(\mathbf {x})\) of the polynomial fit. In the following text, fitting of the residue is assumed. For clarity, y is used in the equations instead of \(\mathbf {y} - \hat {f}_{\text {regr}}(\mathbf {x})\).
2.1.1 Kriging
A popular method for metamodeling with simulation data is kriging. It has been developed by Krige (1951) and became popular in engineering design after the work of Sacks et al. (1989). The data is assumed to be a realization of a Gaussian random field. The spatial correlation between two points x (i) and x (j) is assumed to be:
The number of dimensions is k. For any correlation function, the prediction \(\hat {f}\) and Mean Squared Error (MSE) estimate \(\hat {s}^{2}\) at any point x can be derived (Forrester et al. 2008):
In these equations ϕ is a vector with the correlation between point x and all observations x (i). The n×n matrix Φ contains the correlations between all observation points x (i). The model parameters 𝜃 and p are found through maximization of the likelihood function L(𝜃, p) (Forrester and Keane 2009):
The exponents p are related to the smoothness of the function (Jones et al. 1998). Under assumption that the underlying function f is smooth, the values of p can be set to 2 and only the 𝜃 parameters have to be optimized. The ability to fit complex nonlinear models and to estimate the prediction uncertainty attracted many researchers in the field of sequential optimization to the use of kriging interpolation.
2.1.2 Radial basis functions
In RBF interpolation a set of n axisymmetrical basis functions ψ are placed at the location of each observation point x (i). The function ψ (i) is a function of the Euclidean distance between the points x (i) and x and may have additional parameters.
The n weight factors w i can be solved with the n interpolation equations \(\hat {f}(\mathbf {x}^{(i)}) = y^{(i)}\), leading to w = Ψ −1 y. Hence, the prediction becomes:
The resemblance to the kriging prediction (10) is clear. The procedure for construction of ψ and Ψ is identical to the procedure for ϕ and Φ. Choosing the Gaussian basis function (7) with the same model parameters obviously yields the same prediction. However, kriging is constrained to functions which are decaying from the center point, whereas any function may be used in the more general RBF formulation. Several basis functions have been proposed in literature, such as Gaussian, thin plate spline, multiquadric, inverse multiquadric and others (Fornberg and Zuev 2007). The Gaussian basis function is most frequently used, but the multiquadric basis function (Hardy 1971) has proven to have good predictive capability in several comparative studies (Franke 1982; Jin et al. 2001):
The shape of the Gaussian and the multiquadric basis function with varying model parameters is shown in Fig. 2. A major advantage of RBF over kriging is the possibility to use different shape parameter values c i at each observation point x (i). This is especially desired in the case of unevenly distributed DOE’s, such as the ones obtained by sequential optimization (Fornberg and Zuev 2007).
As stated before, an estimate of the prediction uncertainty is required for sequential sampling. Some researchers derived formulations for the prediction uncertainty for RBF. Li et al. (2010) fit a RBF with Gaussian basis functions with a single parameter for the kernel width using LOOCV. They assume the prediction \(\hat {f}(\mathbf {x})\) to be a realization of a stochastic process and assume the variance of the stochastic process to be ψ(0)−ψ T Ψ −1 ψ (Gibbs 1997; Sóbester et al. 2004; Ji and Kim 2013). This uncertainty measure is applicable for basis functions which are decaying from the center point. A more general uncertainty measure is given by Yao et al. (2014), which derive the relation between the unknown weight factor w at an untried point x with the error of the prediction \(f(\mathbf {x}) - \hat {f}(\mathbf {x})\). They predict the weight factor \(\hat {w}(\mathbf {x})\) by interpolating the weight factors with a RBF model with the same model parameters as the underlying model for the prediction \(\hat {f}(\mathbf {x})\). The disadvantage of this measure is that the prediction uncertainty reduces to zero for points which are far away from all DOE points. Nikitin et al. (2012) propose to directly interpolate the LOOCV values at all observation points. However, it is not clear how this uncertainty measure should be used for sequential optimization, since the uncertainty value at the DOE points is not equal to zero. Therefore, we propose a new uncertainty measure in Section 3 with two parameters which is determined with the LOOCV values and a likelihood function.
2.2 Sequential improvement
Due to the computational cost of the simulations, efficient exploration of the design space is required. This can be achieved with sequential improvement strategies. The concepts of sequential improvement will be first explained for the deterministic case with the objective to minimize f and thereafter the robust optimization case will be discussed.
An important question is whether to search in the neighbourhood of the optimum of the predictor \(\hat {f}\) or to search in a region with high prediction uncertainty. The former is denoted as local search and can be achieved by sampling \(\min _{\mathbf {x}} \hat {f}(\mathbf {x})\) whereas the latter is denoted as global search and can be achieved by sampling \(\max _{\mathbf {x}} \hat {s}^{2}(\mathbf {x})\).
Jones et al. (1998) proposed a sequential improvement criterion that combines local and global search in a single measure. The lowest value of y in the current dataset D is y min = min(y). An improvement function is defined as max{y min−y,0}. The predicted value at an unknown point x has the probability \(p_{y} \sim \mathcal {N}(\hat {f}(\mathbf {x}),\hat {s}^{2}(\mathbf {x}))\). Hence, the expected value of the improvement at x is:
with ϕ and Φ the Probability Density Function (PDF) and the Cumulative Distribution Function (CDF) of a standard normal distribution. The term with Φ relates to local search and the term with ϕ relates to global search. Therefore, Sóbester et al. (2004) proposed to include a weight factor w∈[0,1] to be able to adapt the inclination towards local or global search:
When constraints are included in the optimization problem, it is unwise to sample new points at locations with high probability of not fulfilling the constraints. Therefore, it is proposed to multiply the expected improvement with the probability of fulfilling the constraints (Lehman et al. 2004; Forrester and Keane 2009):
In the case of robust optimization a clear distinction should be made between uncertainty over the predictor \(\hat {f} (\mathbf {x},\mathbf {z})\) which is defined in (x, z) and uncertainty over the objective function value \(\text {Obj} (\hat {Y} (\mathbf {x}) )\) which is defined in x. Estimating the latter enables the use of an improvement criterion similar to (15). In the case of using μ Y + kσ Y as objective function the mean MSE can be used as an estimate of the objective function MSE (Jurecka et al. 2007; Wiebenga 2014):
The sequential improvement procedure for robust optimization is split in two steps: first a location in the design space x is selected based on expected improvement, thereafter the location in the noise space z is selected. At any point in the design space x an estimate of the objective function value \(\text {Obj} (\hat {Y} (\mathbf {x}) )\) and an estimate of its uncertainty \(\hat {s}_{\text {Obj}} (\mathbf {x}) \) can be determined. In contrast to the deterministic optimization case, there is not a clearly defined best point y min in the design space, since the prediction error \(\hat {s}_{\text {Obj}} (\mathbf {x})\) is larger than zero for any x. Some authors propose to define the best point x b as the point {x b ∈x (i):i = 1…n} with the lowest value for the objective function prediction (Jurecka 2007; Wiebenga et al. 2012). In this work a different criterion is used. The criterion and the reasoning behind it are discussed in Section 6.2.
Now a criterion is needed to quantify whether a candidate infill point x can potentially yield an improvement over the current best solution x b , given \(\text {Obj}(\hat {Y}(\mathbf {x}))\), \(\hat {s}_{\text {Obj}}(\mathbf {x})\), \(\text {Obj}(\hat {Y}(\mathbf {x}_{b}))\) and \(\hat {s}_{\text {Obj}}(\mathbf {x}_{b})\). One approach is to ignore the prediction error at the best point \(\hat {s}_{\text {Obj}}(\mathbf {x}_{b})\) and use the criterion of (15) (Jurecka et al. 2007). Note that selecting the current best point as candidate infill point x = x b yields a nonzero value of the expected improvement. Clearly it is desired to sample more points at x b to decrease the prediction error of the current best estimate.
To our knowledge there has been only one criterion proposed which includes the prediction uncertainty \(\hat {s}_{\text {Obj}}(\mathbf {x}_{b})\) and is suitable for metamodel based sequential robust optimization. Jurecka (2007) proposed to replace the probability p y in (15) with \(\max \{p_{\text {Obj}(\mathbf {x})}-p_{\text {Obj}(\mathbf {x}_{b})},0\}\). A graphical representation of the new probability is shown in Fig. 3. Note that \(\int p_{y} \leq 1\). The reasoning behind this approach is that the probability for a certain objective function value at x should only be taken into account if it is higher than the probability of the same outcome at x b . However, a new DOE point will never be picked at x b because the expected improvement value at x = x b is zero.
Probability of the objective function value for x b and x. The expected improvement criterion of Jurecka (2007) is calculated with the probability given by the hatched area
The last step of the sequential improvement procedure is to select a location in the noise space z at the selected location in the design space x ′. The purpose of the new simulation is to improve the prediction of \(\text {Obj}(\hat {Y}(\mathbf {x}^{\prime }))\). Hence criteria such as \(\arg \!\max _{\mathbf {z}} \hat {s}^{2} (\mathbf {x}^{\prime },\mathbf {z})\) (Jurecka et al. 2007) or \(\arg \!\max _{\mathbf {z}} (\hat {s}^{2} (\mathbf {x}^{\prime },\mathbf {z}) p_{\mathbf {Z}}(\mathbf {z}))\) (Jurecka 2007; Wiebenga et al. 2012) can be used for this purpose.
The abovementioned sequential improvement criteria can be regarded as global improvement criteria, in the sense that a criterion which is defined in the complete function domain is to be minimized to obtain a new infill point. A different class of sequential improvement methods is given by trust region strategies. Trust region strategies work with metamodels (also referred to as approximation models) which can be trusted within a certain trust region. The size and position of the trust region and the metamodel itself are updated based on evaluations of a high-fidelity model in a local search procedure. Hence, the choice of a new infill point is determined by the search path of the algorithm. The algorithm has been extended from local quadratic approximation models to any kind of approximation models by Alexandrov et al. (1998). One specific application of trust region strategies is to solve optimization problems using variable fidelity models which are coupled through mapping functions. Gano et al. (2006) used kriging interpolation functions to map variable fidelity models in a trust region optimization procedure. For further reading we refer to the application of trust region strategies to different engineering problems, such as the design of an autonomous hovercraft (Rodríguez et al. 2001) and the weight minimization of a fiber-reinforced cantilever beam (Zadeh et al. 2009).
This concludes the overview of the building blocks of the robust sequential optimization algorithm. In Section 3 an implementation of a RBF model is proposed, including estimation of the prediction error. In Section 4 a novel expected improvement criterion for robust optimization is proposed, including a discussion on the several criteria available for robust optimization. The effectiveness of these building blocks will be compared with other methods in Section 7.
3 RBF with uncertainty measure
As discussed in Section 2.1.2, there is a lot of freedom for the user on the exact implementation of the RBF method. Therefore, a proposal is made for an implementation for efficient sequential optimization. The procedure is elaborated in this section and the implementation choices are discussed.
As mentioned in Section 2.1, the first step is to normalize the dataset D and capture the global trend with a polynomial model. The residue of the polynomial model is fit with the RBF model. The basis functions ψ (i) (12) are a function of the Euclidean distance ||x (i)−x|| in the normalized space. However, the sensitivities of the function f to the different normalized variables are expected to be strongly varying. Hence it is inefficient to let the basis functions have an equal influence in each normalized direction. Therefore, it is proposed to scale the effect of the basis functions into each dimension with a scaling parameter 𝜃, which is similar to what is done in kriging (7):
The symbol ∘ is the Hadamard product and denotes pointwise multiplication. The vector 𝜃 has the same size as the vector x and scales each dimension of x. It is proposed to use the multiquadric (14) basis function or the following form of the Gaussian basis function:
After several iterations of the sequential optimization algorithm, the dataset D starts to become unevenly distributed over the input space: the algorithm adds sampling points in the region with high probability of improvement and ignores regions with low probability of improvement. The shape parameter c i determines the range of influence of basis function ψ (i) (see Fig. 2). For unevenly distributed DOE’s, it is unwise to use the same shape parameter for both dense and sparse sampled regions of the dataset D. However, optimizing all shape parameters c i is computationally too expensive. Therefore, it is chosen to couple the local shape parameters c i to the distance to its nearest neighbor:
First, the scaled distance to the nearest neighbor d i is determined with (21). Thereafter, the distance to the nearest neighbor is normalized with (22), such that c i ≤1∀c i holds. The latter operation is needed, to ensure that each value for the scaling parameter 𝜃 results in a unique metamodel. Note that the scaling parameter 𝜃 has not yet been selected and can be freely chosen. When the scaling parameter 𝜃 is multiplied with a constant C, the scaled distance to the nearest neighbors d i changes accordingly (d i (C 𝜃) = Cd i (𝜃)). If the local shape parameters are set to the distance to the nearest neighbor (c i = d i ), the relative effect of basis function ψ (i) throughout the scaled model space (𝜃∘x) will remain the same when multiplying the scaling parameter 𝜃 with a constant. Hence, all models with parameter sets C 𝜃 ∀C > 0 will be equal. To avoid this effect, the normalization from (22) is used.
In Fig. 4 the effect of this approach is illustrated. With constant shape parameters either a bad prediction in sparse sampled areas or severe oscillations in dense sampled areas and a badly conditioned matrix Ψ are obtained. However, scaling the shape factors c i based on the local point density yields a good fit in all regions the model. Note that changing the shape parameters c i changes the width of the basis function and the effect of the scaling parameter 𝜃.
The optimal values for the scaling parameters 𝜃 (19) are determined based on the LOOCV value. Rippa (1999) derived that the cross-validation values can be determined with minimal computational cost:
The optimal scaling parameters 𝜃 are determined by minimization of the L 2 norm of the error ||𝜖||2. The number of components of 𝜃 equals the number of dimensions of the metamodel.
The last step of the fitting procedure is the estimation of the fitting error. The proposed approach is to assume a certain function for the uncertainty and fit the function parameters based on the LOOCV values. It is assumed that the prediction uncertainty at point x is a function of the distance in the scaled model space (𝜃∘x) between point x and all observations x (i). As with kriging interpolation and as required with the discussed sequential improvement criteria, the uncertainty at any point x is characterized with a standard deviation. It is assumed that the model uncertainty is zero at the DOE points and saturates to \(\hat {s}_{\max }\) at points far from the DOE points. A straightforward assumption for the uncertainty function \(\psi _{\hat {s}}\) is the Gaussian basis function, which is also commonly used as uncertainty (and fitting) function in kriging interpolation. With one model parameter 𝜃 s , the uncertainty function becomes:
Note that other assumptions may be made for the uncertainty function \(\psi _{\hat {s}}\). Such an assumption may depend on the available data and on the chosen RBF basis function for fitting the metamodel. In this work, satisfying results have been obtained with the chosen uncertainty function. The model parameters 𝜃 s and \(\hat {s}_{\max }\) are determined by maximizing the ln-likelihood of the LOOCV values:
with:
with ϕ being the PDF of a standard normal distribution.
4 Robust expected improvement
The novel expected improvement criterion for robust optimization is based on the criterion for deterministic optimization of Jones et al. (1998) (15). As stated in Section 2.2, the problem with robust optimization is that the best objective function value up to a certain iteration of the optimization procedure is just an estimation and therefore not exactly known. Hence, both objective function values at the best point x b and the candidate point x are characterized by the probabilities \(p_{\text {Obj}_{b}} \sim \mathcal {N}(\text {Obj} (\hat {Y} (\mathbf {x}_{b}) ) ,\hat {s}^{2}_{\text {Obj}}(\mathbf {x}_{b}))\) and \(p_{\text {Obj}} \sim \mathcal {N}(\text {Obj} (\hat {Y} (\mathbf {x}) ) ,\hat {s}^{2}_{\text {Obj}}(\mathbf {x}))\) respectively. Equivalently to the deterministic approach, an improvement function is defined based on the real - but still unknown - objective function values at x b and x:
Given the probabilities \(p_{\text {Obj}_{b}}\) and p Obj and the improvement function, an expected value of the improvement can be determined. For clarity, Obj is renamed to μ and \(\hat {s}_{\text {Obj}}\) is renamed to \(\hat {s}\):
which is derived to be:
The full derivation can be found in the Appendix. With zero uncertainty \(\hat {s}_{b}\) of the objective at x b the equation reduces to (15).
In Sections 5 and 7 the efficiency of the novel criterion for sequential improvement is compared with the efficiency of the criteria of Jones et al. (1998) and Jurecka (2007). Some observations on the differences between these criteria can be made when investigating the functions. At first, the three criteria are identical when the objective uncertainty at the best point is zero. In Fig. 5 the expected improvement functions are shown for the case that the uncertainty at the best point x b is found to be \(\hat {s}_{b} = 0.4\). Obviously, point x b is a candidate infill point because it can be sampled at a new location in the noise space z. Therefore, a candidate point x should have an expected value of at least EI(x b ) to be selected as the new infill point. In the figures, the value of EI(x b ) is marked with a circle ∘. Looking at the difference between the Jones citerion (Fig. 5a) and the novel criterion (Fig. 5c), it is clear that the differences in the region with EI(x)<EI(x b ) are unimportant since the new infill point will never be selected from this region. In the region with EI(x)>EI(x b ) the differences between both criteria are small. In Section 7 it will be shown whether these differences affect the efficiency of the criteria.
When observing the criterion of Jurecka (2007) (Fig. 5b) some remarkable characteristics are seen. First observation is that the expected improvement value at x b equals zero. Therefore, the current best point will never be selected as the new infill point. Also a large region has an EI value close to zero, which makes it difficult for the algorithm to distinct between regions with high and low probability of improvement. Furthermore it is seen that in some regions the EI value decreases with increasing uncertainty \(\hat {s}\), such as around \((\hat {\mu }_{b}-\hat {\mu } = 0.2, \hat {s}=0)\). However if two points would have the same expected value \(\hat {\mu }\), the point with the highest uncertainty \(\hat {s}\) should be preferred. In the Sections 5 and 7 it is examined how these properties of the Jurecka criterion influence its efficiency.
5 Demonstration: Gaussian random fields
The efficiency of the sequential improvement criteria and metamodeling methods for robust optimization have been compared based on a robust optimization test with a large set of Gaussian random fields. The approach and results are presented in Section 5.1 for the sequential improvement criterion and in Section 5.2 for the metamodeling methods.
5.1 Sequential improvement criterion
The efficiency of the three sequential improvement criteria for robust optimization have been compared based on an optimization test with mathematical functions. To eliminate the influence of the metamodeling technique a set of 15000 Gaussian random fields f(x, z) with predefined statistical parameters has been generated. Therefore, the kriging predictor can be used to obtain the best prediction and uncertainty measure given any set of observations D = {((x,z)(i), f(x,z)(i))|i = 1…n}. The random fields have one design parameter x and one noise parameter z in the range [0,1]. The correlation function of the random fields is Gaussian (7) with model parameters p x = 2 and p z = 2. The model parameters 𝜃 x and 𝜃 z are selected randomly from the respective sets {30,40,50…300} and {30,40,50…100}. The probability distribution of the random field f(x,z) is \(p_{f} \sim \mathcal {N}(0,1^{2})\). The probability of the noise parameter z is given by a truncated normal distribution with mean 0.5, standard deviation 0.1, truncated outside the range [0,1]. During the optimization the selection of new infill points is restricted to an equidistant grid of 25 points in x-direction and 21 points in z-direction. As an initial DOE the center point of the field (x,z)=(0.5,0.5) is taken and a total of 50 sequential improvement iterations are performed.
The sequential optimization procedure has been performed for all 15000 random fields with the three optimization algorithms. Selection of z is done with the criterion \(\arg \!\max _{z} (\hat {s}^{2} (x^{\prime },z) p_{z}(z))\). The results are shown in Fig. 6. The correct robust optimum was found after 50 iterations in 92.1 %, 61.3 % and 93.1 % of the cases for the Jones, Jurecka and novel criterion respectively. The novel criterion (Fig. 6c) is slightly more efficient than the Jones criterion (Fig. 6a). It should be noted that the extra computational cost of the novel criterion is negligible since the only difference is that the objective uncertainty \(\hat {s}_{\text {Obj}}\) at the current best point x b has to be included. The statistical significance of the conclusion that the novel criterion is more efficient than Jones’ criterion can be tested with McNemar’s test for paired nominal data (McNemar 1947). Table 1 shows the number of correct solutions after 50 iterations for both criteria. The null hypothesis states that the probability that Jones’ criterion and the novel criterion find the correct solution is the same. The test statistic is χ 2 = (513−367)2/(513+367). The statistic has a chi-squared distribution and the null hypothesis is rejected with a p-value of 8.6e-7. Hence, a statistically significant improvement with the new criterion is found in the test with 2-D Gaussian random fields.
The convergence of the Jurecka criterion is shown in Fig. 6b. During the first 10 iterations the average convergence is similar to the average convergence of the other methods but thereafter the convergence rate drops. Furthermore it is observed that the Jurecka criterion fails to select the correct robust optimum after 50 iterations in 38.7 % of the runs. One cause for the poor convergence is that the current best optimum x b is never selected as an infill point since the expected improvement value at x b equals zero (Fig. 5b). Therefore, it may happen that an underestimated value of the current best optimum x b is not verified by additional samples, leading to erroneous results.
The mathematical test reveals performance differences between the three expected improvement criteria. However limited conclusions should be drawn since only one type of function (2D Gaussian random field) with one metamodeling method (kriging) have been studied. Therefore, all expected improvement criteria are included in the study on the efficiency of the robust optimization procedure of a V-bending process with a Finite Element (FE) model with seven variables. The study is presented in Section 6.
5.2 Metamodeling method
As reported in the comparative studies of Franke (1982) and Jin et al. (2001), different problems may require different types of metamodels. To reflect this, four different sets of 2000 Gaussian random fields have been generated for a study on the effect of metamodeling methods on the efficiency of the optimization procedure. Each set has fixed statistical parameters. Two of these sets have additional normal distributed white noise with standard deviation σ n. The parameters of the different sets are listen in Table 2.
For each Gaussian random field, the same optimization procedure has been followed as in Section 5.1, except for the details mentioned in this paragraph. The novel criterion for sequential improvement has been used. A small initial DOE is used, with a full factorial design (four points) and six additional latin hypercube design points. Thereafter, 50 sequential optimization iterations have been performed. During the optimization the selection of new infill points is restricted to an equidistant grid of 101 points in x-direction and 21 points in z-direction. As metamodeling methods, kriging, RBF with Gaussian basis functions (RBFG) and RBF with multiquadric basis functions (RBFMQ) have been used. A constant value has been used to detrend the data for all metamodeling methods. Note that fitting of the kriging model requires determination of the statistical parameters (11), whereas the kriging model in Section 5.1 was fit with known statistical parameters.
It does not make sense to assess the quality of the metamodels with the estimate of the metamodel uncertainty at the real robust optimum, as done in Section 5.1, because the uncertainty estimates of the metamodels are not exact, whereas the best possible metamodel (wich exact uncertainty estimate) was used in the previous section. Therefore, another measure is used to assess the quality of the metamodels. In each run, the optimum is determined after each iteration and the difference between the real objective function value at this predicted optimum and the real objective function value at the real optimum is defined as the potential improvement PI:
The average potential improvement over all 2000 runs in each set is shown in Fig. 7. With increasing number of iterations, the potential improvement converges to zero. For the runs without noise (σ n = 0, Fig. 7a and b), the kriging metamodel performs best. This is expected, because the studied functions are Gaussian random fields, which are built with the same assumptions as used for kriging interpolation. However, kriging performs worst for the case with additional noise (σ n = 0.2, Fig. 7c and d). The RBF metamodels are less sensitive to additional noise because the distance between DOE points is taken into account in the implementation (22). Therefore, large differences in function value for nearby points due to noise do not have a large effect on the metamodel quality. This example is relevant for metamodel based optimization with numerical models, because numerical models may suffer from numerical noise (Wiebenga and van den Boogaard 2014).
Potential improvement PI (30) averaged over 2000 runs for kriging ( ), RBFG (
), RBFG ( ) and RBFMQ (
) and RBFMQ ( ): set 1 (a), set 2 (b), set 3 (c) and set 4 (d)
): set 1 (a), set 2 (b), set 3 (c) and set 4 (d)
A quantitative comparison between the effect of different metamodels on the robust optimization procedure is given in Table 3. For each run, the real objective function value is determined at the predicted optimum. In a comparison between two types of metamodels, it is listed how frequently each metamodel yields a better solution after 50 iterations. Based on McNemar’s statistical test for paired data, the statistical relevance of each comparison is listed (the procedure for determining the p-value with McNemar’s test has been discussed in Section 5.1). The results with a p-value lower than 0.001 are regarded as statistically significant. It can be concluded for this test that kriging has a higher chance of finding a lower objective function value in the case without noise, whereas RBFMQ has a higher chance than kriging of finding a better optimum when noise is present.
The comparison of the effect of metamodeling methods on the efficiency of the robust optimization procedure shows that the choice for the best metamodel depends on the problem at hand. To assess the effect of the discussed metamodeling methods in a real engineering problem, the robust optimization problem of a V-bending metal forming process is presented in the following section.
6 Demonstration process: V-bending
The effect of the use of different metamodeling methods and sequential sampling criteria on the effectiveness of the robust optimization procedure are investigated based on the robust optimization of a steel strip bending process (Fig. 8). This process has been optimized previously with four design variables and two noise variables (Wiebenga et al. 2012). In the present work the number of design variables is set to five and again two noise variables are used. In Section 6.1 the used numerical model and the optimization problem are explained. In Section 6.2 an overview of the full optimization algorithm is given.
6.1 V-bending model
An impression of the V-bending process is given in Fig. 8. The sheet is deformed during the downward movement of the punch. After a prescribed depth is reached, the punch moves upwards and the strip reaches its final angle after elastic springback. For good performance of the product the final geometry should meet certain specifications. A main angle 𝜃 M and a transition angle 𝜃 T are defined (Fig. 9). The main angle 𝜃 M should be 90° and the transition angle 𝜃 T should stay within the constraints 92°≤𝜃 T ≤ 96°.
It is assumed that the process suffers from two variation types: variation of the sheet thickness t with \(p_{t} \sim \mathcal {N}(0.51,0.01^{2})\) and variation of the yield stress σ y with \(p_{\sigma _{y}} \sim \mathcal {N}(350,6.66^{2})\). Five design variables are included in the optimization: the tool angle α, the final depth of the stroke D, the geometrical parameter L and two different radii of the tooling R 1 and R 2 (see Fig. 10). Obviously the process is strongly nonlinear and many interactions between the variables are expected. The significance of the used variables is discussed in Wiebenga et al. (2012). The full optimization problem is stated as follows:
A 2D FE model has been built for the optimization. The implicit MSC.Marc solver has been used. Plane strain condition is assumed in the model and the die and punch have been modeled with elastic quadrilateral elements. A half sheet has been modeled with 500 quadrilateral elements due to symmetry. The elasticity of the tooling and the sheet is set to 210 GPa. Isotropic hardening and Von Mises yield criterion are used for the sheet. An experimentally obtained hardening curve is implemented in the model with a tabular input.
The numerical stability of the model is of utmost importance for the optimization procedure. The effect of numerical noise on metamodel based optimization has been studied by Wiebenga and van den Boogaard (2014). The order of variation due to numerical noise should be lower than the order of variation caused by variation of noise variables. To ensure this, it is highly recommended to perform a study on the numerical noise of the model before running the optimization. In our experience, optimizing contact and convergence settings and using fixed time steps in the simulation helped to decrease the numerical noise of the model.
The average simulation time of the model is around 11 minutes. Even though the complexity of the model is limited and the computational cost is reasonable, it is too expensive to perform simulations in the full parameter space. Therefore an efficient optimization scheme is required.
6.2 Optimization algorithm
In this section an overview of the full optimization algorithm is given. The full procedure is implemented in MATLAB. For the initial DOE a resolution IV 27−3 fractional factorial design is used to have some DOE points on the bounds of the domain, combined with a latin hypercube design of 24 points (constructed with default MATLAB settings, meaning that it is optimized with maximin criterion in five iterations) to get a good distribution of the points throughout the full domain. The combined DOE has 40 points, which is sparse for a seven-dimensional nonlinear function but sufficient for starting a sequential optimization procedure. Out of the 40 initial simulations, two simulations failed. Hence, all runs start with the same set of 38 points.
The next choice is the metamodeling method with its uncertainty measure (Section 2.1). It is chosen to use the same metamodeling method for the main angle 𝜃 M and the transition angle 𝜃 T . The used metamodels are listed in Table 4. The used kriging toolbox has been developed by Lophaven et al. (2002) and corresponds with the description given in Section 2.1.1. The RBF has been implemented following the proposal given in Section 3.
The last step is the sequential improvement procedure (Section 2.2). The objective function value and the uncertainty on the objective function value for a candidate infill point x are determined with Monte Carlo sampling:
A latin hypercube sample of n mc = 50 points with the distribution p Z (z) is used. It is found by experience that this is sufficient to estimate \(\hat {\mu }_{f}\), \(\hat {\sigma }_{f}\) and \(\hat {s}_{\text {Obj}}\) with affordable computational cost and reasonable accuracy.
The three sequential improvement criteria discussed in this work (Jones, Jurecka and the novel criterion) have been used for the V-bending optimization. At each iteration of sequential improvement the expected improvement is determined with respect to a point x b . Other researchers in sequential robust optimization chose {x b ∈x (i):i = 1…n} with the lowest value for the objective function prediction (Jurecka 2007; Wiebenga et al. 2012). However, at the end of the robust sequential optimization procedure, the choice of an optimal design is based on a metamodel with predictive uncertainty \(\hat {s}_{\text {Obj}} (\mathbf {x})\). One could select the design point with the lowest objective function value, but that would probably be reconsidered if the predictive uncertainty \(\hat {s}_{\text {Obj}} (\mathbf {x}_{\text {opt}})\) would be too high. Therefore, selecting an optimal design can be seen as a multi-objective optimization problem on a higher level. Both a low objective function value as well as a low objective function uncertainty are desired. We propose to select the best design by minimizing \(\text {Obj} (\hat {Y} (\mathbf {x}) ) + 6 \hat {s}_{\text {Obj}} (\mathbf {x})\). During sequential improvement, this criterion is used to select the best point x b from the set of already sampled design points {x b ∈x (i):i = 1…n}.
During the sequential optimization procedure some simulations fail to converge. Therefore, a constraint is applied for the sequential improvement criterion that the normalized distance to failed simulations should be higher than 0.1. To examine the convergence behavior of the algorithm, no termination criterion is selected and the runs are continued until a total of 400 successful sequential improvement simulations is reached. Therefore, the final size of the DOE is 38+400=438, which is reasonably sparse for a strongly nonlinear 7-dimensional space. A total of 18 runs are performed: six metamodeling methods times three sequential improvement criteria.
7 Results
All runs have been executed up to 400 iterations. The optimal solutions have been determined after every 50 iterations by minimizing \(\text {Obj} (\hat {Y} (\mathbf {x}) ) + 6 \hat {s}_{\text {Obj}} (\mathbf {x})\) with the constraint that the probability of constraint violation should be less than 1 %. These values have been checked by performing a set of 49 simulations on a 7 by 7 grid in the noise space at every design solution found. The solutions of all runs after 400 iterations are listed in Table 5.
At first, it can be seen by the characteristics of different optima that the process is strongly nonlinear (Fig. 11e–h). The influence of the thickness and the yield stress on the main angle 𝜃 M is strongly dependent on the design variables. A striking example of the nonlinearity is the local minimum of the angle for the Jones criterion - RBFG0 run at a thickness of 0.52 mm (Fig. 11e), whereas the Jurecka criterion - RBFMQ0 optimum has a local maximum at the same thickness (Fig. 11g). Hence, is should be clear that the strip bending optimization problem has strong interactions between noise variables and design variables. Therefore, it is not surprising that the metamodel prediction of the optimum is of fluctuating quality (Fig. 11a–d).
Metamodel prediction of the main angle 𝜃 M at optimum found after 400 iterations for Jones criterion - RBFG0 (a), Jurecka criterion - kriging0 (b), Jurecka criterion - RBFMQ0 (c) and novel criterion - RBFMQ0 (d). Figures (e–f) show the checked surface corresponding to figures (a–d) respectively. The black dots represent the 7 by 7 grid where the simulations were performed
Obviously, it is not possible to know the global optimum for sure without performing an excessive amount of FE model runs. Therefore, it is not feasible to compare the convergence of the global optimum for all runs. However, the goal of a robust optimization run is to find a good solution of the optimization problem with moderate computational effort. Looking at the results in Table 5, it can be seen that the found optima have a checked objective function value in between 0.14° (novel criterion - RBFG0) and 0.72° (Jurecka - RBFG0). The objective function value is underestimated for 15 out of 18 runs. Only one run has constraint violations. Furthermore the RMSE (\(\hat {s}_{\text {Obj}}\)) is underestimated in 17 out of 18 runs for both the 𝜃 M metamodel as well as for the 𝜃 T metamodel. This is expected since the optimum is selected based on \(\text {Obj} (\hat {Y} (\mathbf {x}) ) + 6 \hat {s}_{\text {Obj}} (\mathbf {x})\), which includes both objective function value as well as RMSE value. Therefore, it is more probable for the optimum to be selected from regions where these values are underestimated. In general it can be said that the robust sequential optimization algorithm yields good results for the V-bending problem. Nearly all results fulfill the constraints and satisfying objective function values have been found. The reference for the objective function value is the best result found with the previous study performed with the same model, where an objective function value of 0.85° was found using four design variables (Wiebenga et al. 2012).
The number of sequential optimization runs is not sufficient to assess the statistical relevance of the results. Hence, it cannot be stated which metamodeling method or sequential improvement criterion is most efficient for robust optimization of the V-bending problem. For statistical relevant results, we refer to the test with mathematical functions in Section 5. However, the V-bending problem results give one example for the performance of the building blocks of the procedure. More general results may be obtained through new studies on the efficiency of the building blocks for other engineering problems. Furthermore, several other conclusions can be drawn based on detailed observation of the results.
Regarding the sequential improvement criteria, mean objective function values of 0.37°, 0.42° and 0.24° are obtained for the Jones, Jurecka and novel criterion runs respectively (Fig. 12). It is worth mentioning the run with Jurecka criterion and RBFMQ1 metamodel. During the first 190 iterations, 183 iterations had an expected improvement value smaller than 10−10 degrees. Hence, the algorithm was not able to distinguish between regions with high and low probability of improvement. During these iterations new DOE points were added throughout the whole domain, until the uncertainty in the best point \(\hat {s}_{\text {Obj}}(\mathbf {x}_{b})\) decreased, enabling the algorithm to find regions with a higher expected improvement value. This artifact clearly influences the performance of the criterion, as discussed in Section 4. However, it is noticeable that finally a good objective function value of 0.18° was found with this run.
Checked objective function values averaged over all runs with the same expected improvement criterion (markers). The averaged metamodel prediction of the objective function value is bounded by \(\text {Obj} (\hat {Y} (\mathbf {x}) ) \pm \hat {s}_{\text {Obj}} (\mathbf {x})\), for the Jones ( ), Jurecka (
), Jurecka ( ) and novel criterion (
) and novel criterion ( )
)
Looking at the metamodeling techniques, the RBF runs outperformed the kriging runs with a small margin, with final mean objective function values of 0.40°, 0.33° and 0.30° for the kriging, Gaussian RBF and multiquadric RBF runs respectively (Fig. 13). Another measure for the quality of the metamodels is their R 2 value. This has been estimated for all iterations based on 5000 simulations, sampled with a latin hypercube design (Fig. 14). The R 2 value is a measure of the predictive quality of the metamodels throughout the full domain, although it is only of interest how the regions with low objective function value are predicted. However, Fig. 14 is of interest because it gives an impression about the stability of the metamodeling methods. During some iterations a strong drop in the R 2 value is observed. Recall that the fitting procedure for kriging and RBF includes the optimization of model parameters based on a likelihood measure. This measure can be strongly affected by the addition of an extra DOE point, yielding to a different set of model parameters and a sudden drop in the R 2 value of the metamodel. It may be expected that these fluctuations in the predictive capability of the metamodel negatively affect the efficiency of the optimization. From Fig. 14 it can be seen that the RBF metamodels suffer less from these strong variations in global fitting accuracy.
Checked objective function values averaged over all runs with the same metamodeling method (markers). The averaged metamodel prediction of the objective function value is bounded by \(\text {Obj} (\hat {Y} (\mathbf {x}) ) \pm \hat {s}_{\text {Obj}} (\mathbf {x})\), for kriging ( ), RBFG (
), RBFG ( ) and RBFMQ (
) and RBFMQ ( )
)
In Fig. 15 the estimated and checked objective function values after every 50 iterations are shown. It would be expected that the objective function value and the prediction uncertainty decrease with increasing number of iterations. However, this is not always the case. Refitting the metamodels at every iteration leads to changing model parameters and subsequently to a changing prediction of the optimum. On average over all runs the predicted and checked objective function values and the prediction uncertainty decrease with increasing number of iterations.
Objective function value predictions and checked values (diamonds) for Jones ( ) (a,d,g,j,m,p), Jurecka (
) (a,d,g,j,m,p), Jurecka ( ) (b,e,h,k,n,q) and novel criterion (
) (b,e,h,k,n,q) and novel criterion ( ) (c,f,i,l,o,r) at optimum determined with \(\text {Obj} (\hat {Y} (\mathbf {x}) ) + 6 \hat {s}_{\text {Obj}} (\mathbf {x})\), with constraint that the probability of constraint violation should be less than 1 %. This constraint could not be fulfilled for the Jones - kriging0 run at 50 iterations and for the Jurecka - kriging0 run at 50, 150 and 200 iterations. The error bars represent the \(\pm \hat {s}_{\text {Obj}} (\mathbf {x})\) range
) (c,f,i,l,o,r) at optimum determined with \(\text {Obj} (\hat {Y} (\mathbf {x}) ) + 6 \hat {s}_{\text {Obj}} (\mathbf {x})\), with constraint that the probability of constraint violation should be less than 1 %. This constraint could not be fulfilled for the Jones - kriging0 run at 50 iterations and for the Jurecka - kriging0 run at 50, 150 and 200 iterations. The error bars represent the \(\pm \hat {s}_{\text {Obj}} (\mathbf {x})\) range
8 Conclusion
In this work the effect of the metamodeling method and the sequential improvement criterion on the efficiency of the robust optimization procedure is investigated.
The only available criterion for sequential improvement in robust optimization was the Jurecka criterion. However, this criterion has some artifacts, such as that, when two points have the same prediction for the objective function value, the point with the largest prediction uncertainty is not always preferred as new sampling point. Furthermore, the current estimate of the best design point has an expected improvement value of zero by definition. Therefore, an erroneously underpredicted objective function value will not be verified with additional simulations, even when the prediction uncertainty is large. Therefore, we propose a new criterion for sequential improvement in robust optimization, which is derived from the deterministic expected improvement criterion of Jones et al. (1998). This criterion shows better performance than the Jurecka criterion and than the deterministic Jones criterion, both in a test with mathematical test functions (Section 5) as well as in a V-bending optimization problem (Section 7). Whereas the validity of this conclusion is shown to be statistically significant for the test with mathematical test functions, no statistical test could be performed based on the small number of optimization runs in the V-bending test. It is recommended to verify the presented observations with new studies on robust optimization in engineering.
Regarding the metamodeling method, kriging has been used by many researchers for sequential optimization. We propose an improved implementation of RBF suitable for sequential optimization, including an estimation of the metamodel uncertainty. In a robust optimization test with mathematical test functions it was shown with statistical significance that kriging metamodels perform best when no noise is present on the black-box function, whereas the proposed implementation of the RBF interpolation function with multiquadric basis functions performs best when noise is present. Hence, it is shown that the choice for the best metamodeling method for robust optimization should depend on the investigated optimization problem. In the test with the optimization of a strongly nonlinear V-bending process the RBF metamodels outperformed the kriging metamodels with a small margin. Furthermore the RBF metamodels proved to suffer less from fluctuations in their global predictive capability throughout the optimization procedure.
Given these observations, we believe that the novel robust sequential improvement criterion as well as the proposed implementation of RBF may be successfully used for other applications in the field of robust optimization and metamodel based optimization respectively. Obviously, the effect on the optimization efficiency may be strongly dependent on the optimization problem at hand. Therefore, we believe that there is no general solution for an optimal sequential optimization algorithm. However, knowing the pros and cons of the available building blocks may significantly improve the chances of success in robust optimization.
References
Alexandrov N, Dennis J, Lewis R, Torczon V (1998) A trust-region framework for managing the use of approximation models in optimization. Struct Optim 15(1):16–23
Beyer H G, Sendhoff B (2007) Robust optimization - a comprehensive survey. Comput Methods Appl Mech Eng 196(33–34):3190–3218
Coelho R, Bouillard P (2011) Multi-objective reliability-based optimization with stochastic metamodels. Evol Comput 19(4):525–560
Fornberg B, Zuev J (2007) The runge phenomenon and spatially variable shape parameters in rbf interpolation. Comput Math Appl 54(3):379–398
Forrester A, Keane A (2009) Recent advances in surrogate-based optimization. Progress Aerospace Sci 45 (1–3):50–79
Forrester A, Sobester A, Keane A (2008) Engineering design via surrogate modelling: a practical guide. Wiley
Franke R (1982) Scattered data interpolation: tests of some method. Math Comput 38(157):181–200
Gano S, Renaud J, Martin J, Simpson T (2006) Update strategies for kriging models used in variable fidelity optimization. Struct Multidiscip Optim 32(4):287–298
Gibbs M (1997) Bayesian gaussian processes for regression and classification. University of Cambridge, PhD thesis
Hardy R L (1971) Multiquadric equations of topography and other irregular surfaces. J Geophys Res 76:1905–1915
Havinga J, Van Den Boogaard T, Klaseboer G (2013) Sequential optimization of strip bending process using multiquadric radial basis function surrogate models. Key Eng Mater 554–557:911–918
Huang D, Allen T, Notz W, Zeng N (2006) Global optimization of stochastic black-box systems via sequential kriging meta-models. J Global Optim 34(3):441–466
Janusevskis J, Le Riche R (2013) Simultaneous kriging-based estimation and optimization of mean response. J Global Optim 55(2):313–336
Ji Y, Kim S (2013) An adaptive radial basis function method using weighted improvement. pp 957–968
Jin R, Chen W, Simpson T (2001) Comparative studies of metamodelling techniques under multiple modelling criteria. Struct Multidiscip Optim 23(1):1–13
Jones D, Schonlau M, Welch W (1998) Efficient global optimization of expensive black-box functions. J Global Optim 13(4):455–492
Jurecka F (2007) Robust design optimization based on metamodeling techniques. PhD thesis
Jurecka F, Ganser M, Bletzinger K U (2007) Update scheme for sequential spatial correlation approximations in robust design optimisation. Comput Struct 85(10):606–614
Kitayama S, Yamazaki K (2014) Sequential approximate robust design optimization using radial basis function network. Int J Mech Mater Des 10(3):313–328
Kleijnen J (2009) Kriging metamodeling in simulation: a review. Eur J Oper Res 192(3):707–716
Koch P, Yang R J, Gu L (2004) Design for six sigma through robust optimization. Struct Multidiscip Optim 26(3–4):235–248
Krige D (1951) A statistical approach to some basic mine valuation problems on the witwatersrand. J Chem Metallur Mining Soc South Africa
Lehman J, Santner T, Notz W (2004) Designing computer experiments to determine robust control variables. Statistica Sinica 14(2):571–590
Leon R V, Shoemaker A C, Kacker R N (1987) Performance measures independent of adjustment: An explanation and extension of taguchi’s signal-to-noise ratios. Technometrics 29(3):253–265
Li C, Wang F L, Chang Y Q, Liu Y (2010) A modified global optimization method based on surrogate model and its application in packing profile optimization of injection molding process. Int J Adv Manuf Technol 48 (5–8):505–511
Lophaven S N, Nielsen HB, Søndergaard J (2002) DACE, A Matlab Kriging Toolbox
Marzat J, Walter E, Piet-Lahanier H (2013) Worst-case global optimization of black-box functions through kriging and relaxation. J Global Optim 55(4):707–727
McNemar Q (1947) Note on the sampling error of the difference between correlated proportions or percentages. Psychometrika 12(2):153–157
Ng E, Geller M (1969) A table of integrals of the error functions. U S Bur Standards-J Res Math Sci 73 B (1):1–20
Nikitin I, Nikitina L, Clees T (2012) Nonlinear metamodeling of bulky data and applications in automotive design. Springer, Berlin, pp 295–301
Nishida Y, Kobayashi H, Nishida H, Sugimura K (2013) Performance improvement of a return channel in a multistage centrifugal compressor using multiobjective optimization. J Turbomach 135(3)
Rhein B, Clees T, Ruschitzka M (2014) Robustness measures and numerical approximation of the cumulative density function of response surfaces. Commun Stat Simul Comput 43(1):1–17
Rippa S (1999) An algorithm for selecting a good value for the parameter c in radial basis function interpolation. Adv Comput Math 11(2–3):193–210
Rodríguez J, Pérez V, Padmanabhan D, Renaud J (2001) Sequential approximate optimization using variable fidelity response surface approximations. Struct Multidiscip Optim 22(1):24–34
Sacks J, Welch W J, Mitchell T J, Wynn H P (1989) Design and analysis of computer experiments. Stat Sci 4(4):409–423
Sóbester A, Leary S, Keane A (2004) A parallel updating scheme for approximating and optimizing high fidelity computer simulations. Struct Multidiscip Optim 27(5):371–383
Sun G, Song X, Baek S, Li Q (2014) Robust optimization of foam-filled thin-walled structure based on sequential kriging metamodel. Struct Multidiscip Optim 49(6):897–913
Taguchi G, Phadke M (1984) Quality engineering through design optimization, pp 1106–1113
Ur Rehman S, Langelaar M, van Keulen F (2014) Efficient kriging-based robust optimization of unconstrained problems. J Comput Sci 5(6):872–881
Wang G, Shan S (2007) Review of metamodeling techniques in support of engineering design optimization. J Mech Des Trans ASME 129(4):370–380
Wiebenga J, van den Boogaard A (2014) On the effect of numerical noise in approximate optimization of forming processes using numerical simulations. Int J Mater Forming 7(3):317–335
Wiebenga J, Van Den Boogaard A, Klaseboer G (2012) Sequential robust optimization of a v-bending process using numerical simulations. Struct Multidiscip Optim 46(1):137–153
Wiebenga J, Atzema E, An Y, Vegter H, Van Den Boogaard A (2014) Effect of material scatter on the plastic behavior and stretchability in sheet metal forming. J Mater Process Technol 214(2):238– 252
Wiebenga J H (2014) Robust design and optimization of forming processes. PhD thesis, Enschede. http://doc.utwente.nl/91096/
Yao W, Chen X, Huang Y, Van Tooren M (2014) A surrogate-based optimization method with rbf neural network enhanced by linear interpolation and hybrid infill strategy. Optim Methods Softw 29(2):406–429
Zadeh P, Toropov V, Wood A (2009) Metamodel-based collaborative optimization framework. Struct Multidiscip Optim 38(2):103– 115
Zimmerman D, Pavlik C, Ruggles A, Armstrong M (1999) An experimental comparison of ordinary and universal kriging and inverse distance weighting. Mathem Geol 31(4):375–390
Author information
Authors and Affiliations
Corresponding author
Appendix: expected improvement for robust optimization
Appendix: expected improvement for robust optimization
The derivation of (29) is given in this section. Starting point is the definition of the expected improvement (28):
with probability distributions:
The solution for the deterministic expected improvement is given by Jones et al. (1998) (15):
using (39) and:
Equations (36) to (41) can be combined and rearranged to:
The three integrals are solved separately. The first integral of (42) results in:
The second integral of (42) can be rewritten using \(y = x - \hat {\mu }_{b}\):
and split into two integrals:
The first integral of (45) can be solved with integration by parts \(\int u \, dv=uv-\int v \, du\):
The first part of (46) equals zero and the second part equals:
Which is the solution of the first integral of (45). The second integral of (45) can be rewritten using \(y = x + \hat {\mu }_{b} - \hat {\mu }\):
Using the substitution rule and \(u = y / (\hat {s} \sqrt {2})\) one gets:
The solution for this integral can be found in Ng and Geller (1969), resulting in:
Hence, the sum of (47) and (50) give the solution of the second integral of (42). The solution of the third integral of (42) is:
Therefore, the solution of (36) is given by replacing the integrals of (42) with (43), (47), (50) and (51):
Rearranging and rewriting using (39) and (41) gives the expected improvement for robust optimization:
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Havinga, J., van den Boogaard, A.H. & Klaseboer, G. Sequential improvement for robust optimization using an uncertainty measure for radial basis functions. Struct Multidisc Optim 55, 1345–1363 (2017). https://doi.org/10.1007/s00158-016-1572-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-016-1572-5




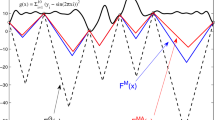




 ) or 𝜃 = 0.3 (
) or 𝜃 = 0.3 ( ) and with varying shape parameters and 𝜃 = 1 (
) and with varying shape parameters and 𝜃 = 1 ( )
)

 ) (a,d), Jurecka (
) (a,d), Jurecka ( ) (b,d) and novel criterion (
) (b,d) and novel criterion ( ) (c,d). RMSE of separate runs is shown with thin gray lines
) (c,d). RMSE of separate runs is shown with thin gray lines








