Skip to main content

Advertisement

SpringerLink
Log in

Local and global Pareto dominance applied to optimal design and material selection of composite structures

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

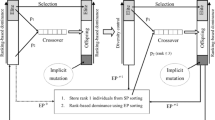
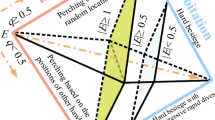
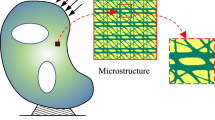
The optimal design of hybrid composite structures considering sizing, topology and material selection is addressed in a multi-objective optimization framework. The proposed algorithm, denoted by Multi-objective Hierarchical Genetic Algorithm (MOHGA), searches for the Pareto-optimal front enforcing population diversity by using a hierarchical genetic structure based on co-evolution of multi-populations. An age structured population is used to store the ranked solutions aiming to obtain the Pareto front. A self-adaptive genetic search incorporating Pareto dominance and elitism is presented. Two concepts of dominance are used: the first one denoted by local non-dominance is implemented at the isolation stage of populations and the second one called global non-dominance is considered at age structured population. The age control emulates the human life cycle and enables to apply the species conservation paradigm. A new mating and offspring selection mechanisms considering age control and dominance are adopted in crossover operator applied to age-structured population. Application to hybrid composite structures requiring the compromise between minimum strain energy and minimum weight is presented. The structural integrity is checked for stress, buckling and displacement constraints considered in the multi-objective optimization. The design variables are ply angles and ply thicknesses of shell laminates, the cross section dimensions of beam stiffeners and the variables associated with the material distribution at laminate level and structure level. The properties of the proposed approach are discussed in detail.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  • António CC, Hoffbauer LN (2009) An approach for reliability-based robust design optimisation of angle-ply composites. Compos Struct 90:53–59

    Article  Google Scholar 

  • Awad ZK, Aravinthan T, Zhuge Y, Gonzalez F (2012) A review of optimization techniques used in the design of fibre composite structures for civil engineering applications. Mater Des 33:534–544

    Article  Google Scholar 

  • Baier H, Huber M, Langer H (2008) Design optimization of hybrid material structures. Struct Multidisc Optim 36:203–213

    Article  Google Scholar 

  • Budiansky B (1974) Theory of buckling and post-buckling of elastic structures. Adv Appl Mech 14:2–63

    Google Scholar 

  • Chun J-S, Kim M-K, Jung H-K (1997) Shape optimization of electromagnetic devices using Immune Algorithm. IEEE Trans Magnet 33:1876–1879

    Article  Google Scholar 

  • Conceição António CA (2002) A multilevel genetic algorithm for optimization of geometrically non-linear stiffened composite structures. Struct Multidisc Optim 24:372–386

    Article  Google Scholar 

  • Conceição António CA (2006) A hierarchical genetic algorithm with age structure for multimodal optimal design of hybrid composites. Struct Multidisc Optim 31:280–294

    Article  Google Scholar 

  • Conceição António C (2009a) Self-adaptation procedures in genetic algorithms applied to the optimal design of composite structures. Int J Mech Mater Des 5:289–302

    Article  Google Scholar 

  • Conceição António CA (2009b) A study on synergy of multiple crossover operators in a hierarchical genetic algorithm applied to structural optimization. Struct Multidisc Optim 38:117–135

    Article  Google Scholar 

  • Conceição António CA, Torres Marques A, Soeiro AV (1995) Optimization of laminated composite structures using a bilevel strategy. Compos Struct 33:193–200

    Article  Google Scholar 

  • Conceição António CA, Trigo Barbosa J, Simas Dinis L (2000) Optimal design of beam reinforced composite structures under elasto-plastic loading conditions. Struct Multidiscipl Optim 19:50–63

    Article  Google Scholar 

  • Crisfield MA (1997) Non-linear finite element analysis of solids and structures, vol 2. Wiley, Chichester

    Google Scholar 

  • Deb K (2001) Multi-objective optimization using evolutionary algorithms. Wiley, Chichester

    MATH  Google Scholar 

  • Fonseca CM, Fleming PJ (1993) Genetic algorithms for multi-objective optimization: formulation, discussion and generalization. In: Forrest S(ed) Proceedings of the fifth international conference on genetic algorithms, San Mateo, California, University of Illinois at Urbana-Champaign. Morgan Kauffman Publishers, San Francisco, pp 416–423

    Google Scholar 

  • Ghiasi H, Pasini D, Lessard L (2010) Pareto frontier for simultaneous structural and manufacturing optimization of composite part. Struct Multidisc Optim 40:497–511

    Article  Google Scholar 

  • Irisarri F-X, Laurin F, Leroy FH, Maire J-F (2011) Computational strategy for multiobjective optimization of composite stiffened panels. Compos Struct 93:1158–1167

    Article  Google Scholar 

  • Kassapoglou C, Dobyns AL (2001) Simultaneous cost and weight minimization of postbuckled composite panels under combined compression and shear. Struct Multidisc Optim 21:372–382

    Article  Google Scholar 

  • Li M, Kou J (2008) Crowding with nearest neighbours replacement for multiple species niching and building blocks preservation in binary multimodal functions optimization. J Heurist 14:243–270

    Article  MATH  Google Scholar 

  • Murugan MS, Suresh S, Ganguli R, Mani V (2007) Target vector optimization of composite box beam using real-coded genetic algorithm: a decomposition approach. Struct Multidisc Optim 33:131–146

    Article  Google Scholar 

  • Pelletier JL, Vel SS (2006) Multi-objective optimization of fiber reinforced composite laminates for strength, stiffness and minimal mass. Comput Struct 84:2065–2080

    Article  Google Scholar 

  • Rahul Sandeep, G, Chakraborty D, Dutta A (2006) Multi-objective optimization of hybrid laminates subjected to transverse impact. Compos Struct 73:360–369

    Article  Google Scholar 

  • Siarry P, Pétrowski A, Bessaou M (2002) A multipopulation genetic algorithm aimed at multimodal optimization. Adv Eng Softw 33:207–213

    Article  MATH  Google Scholar 

  • Spears WM, DeJong SK (1991) On the virtues of parameterized uniform crossover. In: Belew RK, Booker LB(eds) Proceedings of the fourth international conference on genetic algorithms. Morgan Kaufmann, San Mateo, pp 230–236

  • Tang XG, Bassir DH, Zhang WH (2010) Shape, sizing optimization and material selection based on mixed variables and genetic algorithm. Optim Eng 12:111–128

    Article  MathSciNet  Google Scholar 

  • Tsai SW (1987) Composites design. Think composites. Dayton, USA

    Google Scholar 

  • Wang K, Kelly D, Dutton S (2002) Multi-objective optimisation of composite aerospace structures. Compos Struct 57:141–148

    Article  Google Scholar 

Download references

Acknowledgment

The authors acknowledge the financial support provided by the Foundation for Science and Technology (FCT), Portugal, through the strategic project PEst-OE/EME/UI0225/2011.

Author information

Authors and Affiliations

  1. IDMEC, Faculty of Engineering, University of Porto, Rua Dr. Roberto Frias, s/n, 4200-465, Porto, Portugal

    Carlos A. Conceição António

Authors
  1. Carlos A. Conceição António
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Carlos A. Conceição António.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Conceição António, C.A. Local and global Pareto dominance applied to optimal design and material selection of composite structures. Struct Multidisc Optim 48, 73–94 (2013). https://doi.org/10.1007/s00158-012-0878-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-012-0878-1

Keywords

Search

Navigation