Skip to main content
SpringerLink
Log in

Dynamic analysis of box girders with tee-stiffening using unconstrained optimization techniques

  • Research Paper
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

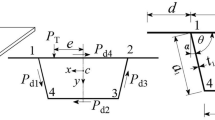
The paper presents a numerical procedure for dynamic analysis of box girders with tee-stiffeners utilizing unconstrained optimization techniques. Unlike the finite element or finite strip methods, the procedure does not require discretization to the whole structure, thus resulting in great savings in computational time. The potential and kinetic energy of the assembled structure is expressed in terms generalized functions that describe the longitudinal and transverse displacement profiles. The problem is then converted into uunconstrained optimization problem to determine the magnitude of the lowest natural frequency and the associated mode shape. Results are presented showing the sensitivity the natural frequency to the stiffener depth (d) and the flange width (b). It is shown that the number of longitudinal and transverse stiffeners largely influence the magnitude of the natural frequency (λ) of the box girder. Design guidelines are also provided to optimize the dynamic response of the structure. The procedure is very practical and can be utilized in the industry for the analysis of box girders.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Barrette M, Berry A, Beslin O (2000) Vibration of stiffened plates using hierarchical trigonometric functions. J Sound Vib 235:727–747

    Article  Google Scholar 

  • Bedair O (2006) Limit state design procedures for static and dynamic analysis of stiffened box girders. Technical report submitted for Bechtel Corporation

  • Bedair O (2009) Analysis and limit state design of stiffened plates and shells: a world view. J Appl Mech Rev 62:76–92

    Google Scholar 

  • Cheung YK, Fan SC (1983) Static analysis of right box girder bridges by spline finite strip method. Proc Inst Civ Eng Part 2 75:311–323

    Google Scholar 

  • Ghavami K, Khedmati R (2006) Numerical and experimental investigations on the compression behaviour of stiffened plates. J Constr Steel Res 62:1087–1100

    Article  Google Scholar 

  • Ghosh A, Biswal K (1996) Free-vibration analysis of stiffened laminated plates using higher-order shear deformation theory. Finite Elem Anal Des 22:143–161

    Article  MATH  MathSciNet  Google Scholar 

  • Harik IE, Guo M (1993) Finite element analysis of eccentrically stiffened plates in free vibration. Comput Struct 49:1007–1015

    Article  MATH  Google Scholar 

  • Harik I, Salamoun G (1988) The analytical strip method of solution for stiffened rectangular plates. Comput Struct 29:283–291

    Article  MATH  Google Scholar 

  • Koko TS (1990) Super finite elements for non-linear static and dynamic analysis of stiffened plate structures. PhD dissertation, University of British Columbia

  • Koko TS, Olson MD (1991) Non-linear analysis of stiffened plates using super element. Int J Numer Methods Eng 31:319–343

    Article  MATH  Google Scholar 

  • Kumar Y, Mukhopadhyay M (2002) Transient response analysis of laminated stiffened plates. Compos Struct 58:97–107

    Article  Google Scholar 

  • Madhavan M, Davidson J (2005) Buckling of centerline-stiffened plates subjected to uniaxial eccentric compression. Thin-Walled Struct 43:1264–1276

    Article  Google Scholar 

  • Mukherjee A, Mukhopadhyay M (1989) Finite element free vibration of eccentrically stiffened plates. Comput Struct 33:295–305

    Article  Google Scholar 

  • Mukhopadhyay M (1989) Vibration and stability of stiffened plates by semi-analytic finite difference method. Part I: consideration of bending displacement only. J Sound Vib 130:27–39

    Article  Google Scholar 

  • Murray NW, Thierauf G (1983) Tables for the design and analysis of stiffened steel plates. Birkhauser, Basel

    Google Scholar 

  • Patel S, Datta P, Sheikh A (2006) Buckling and dynamic instability analysis of stiffened shell panels. Thin-Walled Struct 44:321–333

    Article  Google Scholar 

  • Park B, Cho S (2006) Simple design formulae for predicting the residual damage of unstiffened and stiffened plates under explosion loadings. Int J Impact Eng 32:1721–1736

    Article  Google Scholar 

  • Peng L, Kitipornchai S (2006) Buckling and free vibration analyses of stiffened plates using the FSDT mesh-free method. J Sound Vib 289:421–449

    Article  Google Scholar 

  • Peng-Cheng S, Dade H, Zongmu W (1987) Static, vibration and stability analysis of stiffened plates using B spline functions. Comput Struct 27:73–78

    Article  Google Scholar 

  • Qing G, Qiu J, Liu Y (2006) Free vibration analysis of stiffened laminated plates. Int J Solids Struct 43:1357–1371

    Article  MATH  Google Scholar 

  • Rikards R, Chate A, Ozolinsh O (2001) Analysis for buckling and vibrations of composite stiffened shells and plates. Compos Struct 51:361–370

    Article  Google Scholar 

  • Shen PC, Dade H, Wang Z (1987) Static, vibration and stability analysis of stiffened plates using B-spline functions. Comput Struct 27:73–78

    Article  MATH  Google Scholar 

  • Siddiqi Z, Kukreti A (1998) Analysis of eccentrically stiffened plates with mixed boundary conditions using differential quadrature method. Appl Math Model 22:251–275

    Article  Google Scholar 

  • Wittrick WH (1968) General sinusoidal stiffness matrices for buckling and vibration analysis of thin flat-walled structures. Int J Mech Sci 10:949–966

    Article  MATH  Google Scholar 

  • Zhang W, Wang A, Vlahopoulos N, Wu K (2005) Vibration analysis of stiffened plates under heavy fluid loading by an energy finite element analysis formulation. Finite Elem Anal Des 41:1056–1078

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. OB Engineering Ltd., 116 Mount Aberdeen Manor SE, Calgary, AB, T2Z 3N8, Canada

    Osama Bedair

Authors
  1. Osama Bedair
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Osama Bedair.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bedair, O. Dynamic analysis of box girders with tee-stiffening using unconstrained optimization techniques. Struct Multidisc Optim 42, 547–558 (2010). https://doi.org/10.1007/s00158-010-0499-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-010-0499-5

Keywords

Search

Navigation