International migration and economic growth: a source country perspective

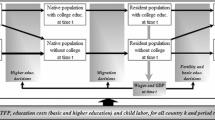
Abstract

This study analyzes the impact of international migration on economic growth of a source country in a stochastic setting. The model accounts for endogenous fertility decisions and distinguishes between public and private schooling systems. We find that economic growth crucially depends on the international migration since the migration possibility will affect fertility decisions and school expenditures. Relaxation of restrictions on the emigration of high-skilled workers will damage the economic growth of a source country in the long run, although a ‘brain gain’ may happen in the short run. Furthermore, the growth rate of a source country under a private education regime will be more sensitive to the probability of migration than a country under a public education regime.

Appendices

Appendix 1

In this appendix, we omit the time index t explicitly to make our derivations easier to read. We should first of all note that the first- and second-order partial derivatives of the utility function with respect to N are:

$$u_{N} = \frac{{\beta {\left( {w_{{\text{B}}} - aw_{{\text{A}}} } \right)}}} {{Nw_{{\text{B}}} + a{\left( {n - N} \right)}w_{{\text{A}}} }} = \frac{{\beta d}} {{Nw_{{\text{B}}} + a{\left( {n - N} \right)}w_{{\text{A}}} }},$$

(14)

$$u_{{NN}} = \frac{{ - \beta d^{2} }} {{{\left[ {Nw_{{\text{B}}} + a{\left( {n - N} \right)}w_{{\text{A}}} } \right]}^{2} }},$$

(15)

where d=w _B−aw _A.

The second-degree Taylor series expansions of the utility function around the mean N=pn is:

$$u \approx u{\left( {pn} \right)} + {\left( {N - pn} \right)}u_{N} {\left( {pn} \right)} + \frac{{{\left( {N - pn} \right)}^{2} }} {{2!}}u_{{NN}} {\left( {pn} \right)}.$$

(16)

Substituting Eqs. (14) and (15) into Eq. (16) and using the statistical results that E(N−pn)=0 and E(N−pn)²=np(1−p), we can derive the expectation of the utility function as:

$$E{\left( u \right)} = u{\left( {pn} \right)} + \frac{{\beta np{\left( {1 - p} \right)}}} {{2!}}{\left\{ { - \frac{{d^{2} }} {{{\left[ {{\left( {pn} \right)}w_{{\text{B}}} + an{\left( {1 - p} \right)}w_{{\text{A}}} } \right]}^{2} }}} \right\}} = u{\left( {pn} \right)} - \frac{{p{\left( {1 - p} \right)}\beta d^{2} }} {{2nw^{2} }},$$

(17)

where w=pw _B+a(1−p)w _A.

Appendix 2

1.1 Proof of proposition 3

We first analyze an economy under a private education regime and then go on to study an economy under a public education regime.

1.1.1 Under a private education regime

Given all parameter values, Eq. 11 implies that the number of children is constant. Hence, from Eq. 12, e _rt is a linear function of h _rt and can be expressed as e _rt =ɛh _rt , where ɛ is a positive number. Equation 2 tells us that human capital in the next period will be $h_{{rt + 1}} = \lambda {\left( {\varepsilon h_{{rt}} } \right)}^{\gamma } h^{{1 - \gamma }}_{{rt}} = \lambda \varepsilon ^{\gamma } h_{{rt}}$. With homogeneous agents, H _rt =h _rt for all t. Therefore, the growth rate of average human capital under a private education regime is:

$$g^{{\text{H}}}_{r} = \frac{{H_{{rt + 1}} }} {{H_{{rt}} }} - 1 = \frac{{h_{{rt + 1}} }} {{h_{{rt}} }} - 1 = \varepsilon ^{\gamma } - 1.$$

(18)

Equation 18 implies that g _r ^H is constant.

1.1.2 Under a public education regime

Under a public education regime, the human capital accumulation function becomes:

$$h_{{ut + 1}} = \lambda e^{\gamma }_{{ut}} h^{{1 - \gamma }}_{{ut}} = \lambda {\left[ {\tau _{t} {\left( {1 - \phi n_{{ut}} } \right)}w_{{\text{A}}} H_{{ut}} } \right]}^{\gamma } h^{{1 - \gamma }}_{{ut}} .$$

(19)

When agents are homogeneous, H _ut =h _ut for all t. This implies that the growth rate under a public education is:

$$g^{{\text{H}}}_{u} = \frac{{H_{{ut + 1}} }}{{H_{{ut}} }} - 1 = \frac{{h_{{ut + 1}} }}{{h_{{ut}} }} - 1 = \lambda {\left[ {\tau _{t} {\left( {1 - \phi n_{{ut}} } \right)}w_{{\text{A}}} } \right]}^{\gamma } - 1.$$

(20)

Because Eqs. 9 and 13 show that given the probability of migration, the tax rate and fertility are constant, Eq. 20 implies that g _u ^H is constant.

QED.

Appendix 3

1.1 Proof of proposition 4

We first consider an economy under a private education regime. Then we study an economy under a public education regime.

1.1.1 Under a private education regime

The left-hand side of Eq. 11 is a function of n _rt and can be expressed by ξ(n _rt ). The right-hand side depends on n _rt and p and can be represented by μ(n _rt ,p). Hence, we can rewrite Eq. 11 as

$$\xi {\left( {n_{{rt}} } \right)} = \mu {\left( {n_{{rt}} ,p} \right)}.$$

(21)

Taking the derivative of both sides of Eq. 21 with respect to p, we get

$${\left( {\frac{{d\xi }}{{dn_{{rt}} }} - \frac{{\partial \mu }}{{\partial n_{{rt}} }}} \right)}n^{\prime }_{{rt}} {\left( p \right)} = \frac{{\partial \mu }}{{\partial p}}.$$

(22)

Note firstly that

$$\frac{{d\xi }} {{dn_{{rt}} }} = \frac{{\phi {\left( {1 + \beta \gamma } \right)}}} {{{\left( {1 - \phi n_{{rt}} } \right)}^{2} }} > 0,$$

(23)

secondly that

$$\frac{{\partial \mu }} {{\partial n_{{rt}} }} = - \frac{{\beta p{\left( {1 - p} \right)}d^{2} }} {{2w^{2} n^{2}_{{rt}} }} < 0,$$

(24)

and thirdly that

$$\frac{{\partial \mu }}{{\partial n_{{rt}} }} = - \frac{{\beta p{\left( {1 - p} \right)}d^{2} }}{{2w^{2} n^{2}_{{rt}} }} < 0,$$

(25)

Substituting the definitions of w and d into the numerator of Eq. 25, we can get

$$\frac{{\partial \mu }}{{\partial p}} = \frac{{\beta d^{2} }}{{2n_{{rt}} }}\frac{{{\left[ { - pw_{{\text{B}}} + a{\left( {1 - p} \right)}w_{{\text{A}}} } \right]}}}{{w^{3} }}.$$

Define p* such that $\frac{{a{\left( {1 - p*} \right)}}}{{p*}} = \frac{{w_{{\text{B}}} }}{{w_{{\text{A}}} }}$. Hence, if $\frac{{\partial \mu }} {{\partial p}} < 0\;if\;p > p*$. Then one must have n _rt ′(p)<0 if p>p* for Eq. 22 to hold. The situation will be reversed ($\frac{{\partial \mu }}{{\partial p}} > 0$ and n _rt ′(p)>0) if p<p*.

From Eq. 12, the derivative of e _rt with respect to n _rt is:

$$\frac{{de_{{rt}} }} {{dn_{{rt}} }} = - \frac{{\beta \gamma w_{{\text{A}}} h_{{rt}} }} {{{\left( {1 + \beta \gamma } \right)}n^{2}_{{rt}} }} < 0.$$

(26)

Using the implicit differentiation of e _rt , we can get that $e^{\prime }_{{rt}} {\left( p \right)} = \frac{{de_{{rt}} }}{{dn_{{rt}} }}n^{\prime }_{{rt}} {\left( p \right)} > 0$ if p>p* and vice versa.

1.1.2 Under a public education regime

The left-hand side of Eq. 13 is a function of n _ut and can be expressed by ξ(n _ut ). The right-hand side depends on n _ut and p and can be represented by μ(n _ut ,p). Hence, we can rewrite Eq. 13 as:

$$\xi {\left( {n_{{ut}} } \right)} = \mu {\left( {n_{{ut}} ,p} \right)}.$$

(27)

Taking the derivative of both sides of Eq. 27 with respect to p, we get

$${\left( {\frac{{d\xi }}{{dn_{{ut}} }} - \frac{{\partial \mu }}{{\partial n_{{ut}} }}} \right)}n^{\prime }_{{ut}} {\left( p \right)} = \frac{{\partial \mu }}{{\partial p}}.$$

(28)

Note firstly that

$$\frac{{d\xi }} {{dn_{{ut}} }} = \frac{{\phi ^{2} }} {{{\left( {1 - \phi n_{{ut}} } \right)}^{2} }} > 0,$$

(29)

secondly that

$$\frac{{\partial \mu }} {{\partial n_{{ut}} }} = - \beta {\left[ {\frac{1} {{n^{2}_{{ut}} }} + \frac{{p{\left( {1 - p} \right)}d^{2} }} {{w^{2} n^{3}_{{ut}} }}} \right]} < 0,$$

(30)

and thirdly that

$$\frac{{\partial \mu }} {{\partial p}} = \frac{{\beta d^{2} }} {{2n^{2}_{{ut}} }}\frac{{{\left[ { - pw_{{\text{B}}} + a{\left( {1 - p} \right)}w_{{\text{A}}} } \right]}}} {{w^{3} }}.$$

(31)

Hence, if $p > p*,\;\frac{{\partial \mu }} {{\partial p}} < 0$. Then from Eq. 28, we know that n _ut ′(p)<0. The situation will be reversed [$\frac{{\partial \mu }}{{\partial p}} > 0$ and n _ut ′(p)>0] if p<p*.

From Eq. 6, the derivative of e _ut with respect to n _ut is

$$\frac{{de_{{ut}} }} {{dn_{{ut}} }} = - \tau \phi w_{{\text{A}}} H_{{ut}} = - \frac{{\beta \gamma \phi }} {{1 + \beta \gamma }}w_{{\text{A}}} H_{{ut}} < 0.$$

(32)

Using the implicit differentiation of e _ut , we can get that $e^{\prime }_{{ut}} {\left( p \right)} = \frac{{de_{{ut}} }}{{dn_{{ut}} }}n^{\prime }_{{ut}} {\left( p \right)} > 0$ if p>p* and vice versa.

QED.

Appendix 4

1.1 Proof of proposition 7

We should first of all note that:

$$\frac{{\partial \theta ^{{\text{L}}}_{{it + 1}} }}{{\partial p^{{\text{H}}} }} = - \frac{{\partial \theta ^{{\text{H}}}_{{it + 1}} }}{{\partial p^{{\text{H}}} }} = \frac{{{\left( {1 - p^{{\text{L}}} } \right)}\theta ^{{\text{L}}}_{i} n^{{\text{L}}}_{{it}} {\left[ {\theta ^{{\text{H}}}_{i} n^{{\text{H}}}_{{it}} - {\left( {1 - p^{{\text{H}}} } \right)}\theta ^{{\text{H}}}_{i} n^{{\text{H}}}_{{it}} \prime {\left( {p^{{\text{H}}} } \right)}} \right]}}}{{{\left[ {{\left( {1 - p^{{\text{L}}} } \right)}\theta ^{{\text{L}}}_{i} n^{{\text{L}}}_{{it}} + {\left( {1 - p^{{\text{H}}} } \right)}\theta ^{{\text{H}}}_{i} n^{{\text{H}}}_{{it}} } \right]}^{2} }} > 0,\;i = r,u.$$

(33)

Under a private education regime, the partial differentiation of H _rt+1 with respect to p ^H can be written as:

$$\frac{{\partial H_{{rt + 1}} }}{{\partial p^{{\text{L}}} }} = \frac{{\partial \theta ^{{\text{L}}}_{{rt + 1}} }}{{\partial p^{{\text{L}}} }}{\left( {h^{{\text{L}}}_{{rt + 1}} - h^{{\text{H}}}_{{rt + 1}} } \right)} + \theta ^{{\text{L}}}_{{rt + 1}} \frac{{\partial h^{{\text{L}}}_{{rt + 1}} }}{{\partial e^{{\text{L}}}_{{rt}} }}e^{{\text{L}}}_{{rt}} \prime {\left( {p^{{\text{L}}} } \right)} + \theta ^{{\text{H}}}_{{rt + 1}} \frac{{\partial h^{{\text{H}}}_{{rt + 1}} }}{{\partial e^{{\text{H}}}_{{rt}} }}e^{{\text{H}}}_{{rt}} \prime {\left( {p^{{\text{L}}} } \right)}.$$

(34)

Since e _rt ^L′(p ^H)=0, Eq. 34 can be expressed as:

$$\frac{{\partial H_{{rt + 1}} }}{{\partial p^{{\text{L}}} }} = \frac{{\partial \theta ^{{\text{L}}}_{{rt + 1}} }}{{\partial p^{{\text{L}}} }}{\left( {h^{{\text{L}}}_{{rt + 1}} - h^{{\text{H}}}_{{rt + 1}} } \right)} + \theta ^{{\text{L}}}_{{rt + 1}} \frac{{\partial h^{{\text{L}}}_{{rt + 1}} }}{{\partial e^{{\text{L}}}_{{rt}} }}e^{{\text{L}}}_{{rt}} \prime {\left( {p^{{\text{L}}} } \right)}.$$

(35)

Because $\frac{{\partial \theta ^{{\text{L}}}_{{rt + 1}} }}{{\partial p^{{\text{L}}} }} < 0$ and $\theta ^{{\text{L}}}_{{rt + 1}} \frac{{\partial h^{{\text{L}}}_{{rt + 1}} }}{{\partial e^{{\text{L}}}_{{rt}} }}e^{{\text{L}}}_{{rt}} \prime {\left( {p^{{\text{L}}} } \right)} > 0$ if p ^H>p*, a sufficient condition for $\frac{{\partial H_{{rt + 1}} }}{{\partial p^{{\text{H}}} }} > 0$ under a private education regime is that $\frac{{\partial \theta ^{{\text{L}}}_{{rt + 1}} }}{{\partial p^{{\text{H}}} }}$ is not too large (that is, an increase in p ^H will not cause a large increase in θ _rt+1 ^L).

Under a public education regime with heterogeneous agents, public school expenditure is:

$$e_{{ut}} = \theta ^{{\text{L}}}_{{ut}} \tau {\left( {1 - \phi n^{{\text{L}}}_{{ut}} } \right)}w_{{\text{A}}} h^{{\text{L}}}_{{ut}} + \theta ^{{\text{H}}}_{{ut}} \tau {\left( {1 - \phi n^{{\text{H}}}_{{ut}} } \right)}w_{{\text{A}}} h^{{\text{H}}}_{{ut}} .$$

(36)

From Eq. 36, we can derive that $e^{\prime }_{{ut}} {\left( {p^{{\text{H}}} } \right)} = \frac{{\partial e_{{ut}} }}{{\partial n^{{\text{H}}}_{{ut}} }}n^{\prime }_{{ut}} {\left( {p^{{\text{H}}} } \right)} > 0$.

The partial differentiation of H _ut+1 with respect to p ^H can be written as:

$$\frac{{\partial H_{{ut + 1}} }}{{\partial p^{{\text{H}}} }} = \frac{{\partial \theta ^{{\text{L}}}_{{ut + 1}} }}{{\partial p^{{\text{H}}} }}{\left( {h^{{\text{L}}}_{{ut + 1}} - h^{{\text{H}}}_{{ut + 1}} } \right)} + {\left[ {\theta ^{{\text{L}}}_{{ut + 1}} \frac{{\partial h^{{\text{L}}}_{{ut + 1}} }}{{\partial e_{{ut}} }} + \theta ^{{\text{H}}}_{{ut + 1}} \frac{{\partial h^{{\text{H}}}_{{ut + 1}} }}{{\partial e_{{ut}} }}} \right]}e^{\prime }_{{ut}} {\left( {p^{{\text{H}}} } \right)}.$$

(37)

Because$\frac{{\partial \theta ^{{\text{L}}}_{{ut + 1}} }}{{\partial p^{{\text{H}}} }} > 0,\,\frac{{\partial h^{{\text{L}}}_{{ut + 1}} }}{{\partial e_{{ut}} }} > 0,\,\frac{{\partial h^{{\text{H}}}_{{ut + 1}} }}{{\partial e_{{ut}} }} > 0$, and e _ut ^H′(p ^H) if p ^H>p*, a sufficient condition for $\frac{{\partial H_{{ut + 1}} }} {{\partial p^{{\text{H}}} }} > 0$ under a public education regime is that $\frac{{\partial \theta ^{{\text{L}}}_{{ut + 1}} }}{{\partial p^{{\text{H}}} }}$ is not too large (that is, an increase in p ^H will not cause a large increase in θ _ut+1 ^L).

QED.

Appendix 5

1.1 Proof of proposition 8

We should first of all note that:

$$\frac{{\partial \theta ^{{\text{L}}}_{{it + 1}} }} {{\partial p^{{\text{L}}} }} = - \frac{{\partial \theta ^{{\text{H}}}_{{it + 1}} }} {{\partial p^{{\text{L}}} }} = \frac{{ - {\left( {1 - p^{{\text{H}}} } \right)}\theta ^{{\text{H}}}_{i} n^{{\text{H}}}_{{it}} {\left[ {\theta ^{{\text{H}}}_{i} n^{{\text{H}}}_{{it}} - {\left( {1 - p^{{\text{L}}} } \right)}\theta ^{{\text{L}}}_{i} n^{{\text{L}}}_{i} \prime {\left( {p^{{\text{L}}} } \right)}} \right]}}} {{{\left[ {{\left( {1 - p^{{\text{L}}} } \right)}\theta ^{{\text{L}}}_{i} n^{{\text{L}}}_{{it}} + {\left( {1 - p^{{\text{H}}} } \right)}\theta ^{{\text{H}}}_{i} n^{{\text{H}}}_{{it}} } \right]}^{2} }} < 0,i = r,u.$$

(38)

Under a private education regime, the partial differentiation of H _rt+1 with respect to p ^L can be written as:

$$\frac{{\partial H_{{rt + 1}} }} {{\partial p^{{\text{L}}} }} = \frac{{\partial \theta ^{{\text{L}}}_{{rt + 1}} }} {{\partial p^{{\text{L}}} }}{\left( {h^{{\text{L}}}_{{rt + 1}} - h^{{\text{H}}}_{{rt + 1}} } \right)} + \theta ^{{\text{L}}}_{{rt + 1}} \frac{{\partial h^{{\text{L}}}_{{rt + 1}} }} {{\partial e^{{\text{L}}}_{{rt}} }}e^{{\text{L}}}_{{rt}} \prime {\left( {p^{{\text{L}}} } \right)} + \theta ^{{\text{H}}}_{{rt + 1}} \frac{{\partial h^{{\text{H}}}_{{rt + 1}} }} {{\partial e^{{\text{H}}}_{{rt}} }}e^{{\text{H}}}_{{rt}} \prime {\left( {p^{{\text{L}}} } \right)}.$$

(39)

Since e _rt ^H′(p ^L)=0, Eq. 39 can be expressed as:

$$\frac{{\partial H_{{rt + 1}} }}{{\partial p^{{\text{L}}} }} = \frac{{\partial \theta ^{{\text{L}}}_{{rt + 1}} }}{{\partial p^{{\text{L}}} }}{\left( {h^{{\text{L}}}_{{rt + 1}} - h^{{\text{H}}}_{{rt + 1}} } \right)} + \theta ^{{\text{L}}}_{{rt + 1}} \frac{{\partial h^{{\text{L}}}_{{rt + 1}} }}{{\partial e^{{\text{L}}}_{{rt}} }}e^{{\text{L}}}_{{rt}} \prime {\left( {p^{{\text{L}}} } \right)}.$$

(40)

Because $\frac{{\partial \theta ^{{\text{L}}}_{{rt + 1}} }} {{\partial p^{{\text{L}}} }} < 0$ and $\theta ^{{\text{L}}}_{{rt + 1}} \frac{{\partial h^{{\text{L}}}_{{rt + 1}} }} {{\partial e^{{\text{L}}}_{{rt}} }}e^{{\text{L}}}_{{rt}} \prime {\left( {p^{{\text{L}}} } \right)} > 0$ if p ^L>p*, from Eq. 40, we have $\frac{{\partial H_{{rt + 1}} }} {{\partial p^{{\text{L}}} }} > 0$.

Under a public education regime, from Eq. 36, we can derive that

$$e^{\prime }_{{ut}} {\left( {p^{{\text{L}}} } \right)} = \frac{{\partial e_{{ut}} }}{{\partial n^{{\text{L}}}_{{ut}} }}n^{\prime }_{{ut}} {\left( {p^{{\text{L}}} } \right)} > 0.$$

The partial differentiation of H _ut+1 with respect to p ^L can be written as:

$$\frac{{\partial H_{{ut + 1}} }}{{\partial p^{{\text{L}}} }} = \frac{{\partial \theta ^{{\text{L}}}_{{ut + 1}} }}{{\partial p^{{\text{L}}} }}{\left( {h^{{\text{L}}}_{{ut + 1}} - h^{{\text{H}}}_{{ut + 1}} } \right)} + {\left[ {\theta ^{{\text{L}}}_{{ut + 1}} \frac{{\partial h^{{\text{L}}}_{{ut + 1}} }}{{\partial e_{{ut}} }} + \theta ^{{\text{H}}}_{{ut + 1}} \frac{{\partial h^{{\text{H}}}_{{ut + 1}} }}{{\partial e_{{ut}} }}} \right]}e^{\prime }_{{ut}} {\left( {p^{{\text{L}}} } \right)}.$$

(41)

Because $\frac{{\partial \theta ^{{\text{L}}}_{{ut + 1}} }}{{\partial p^{{\text{L}}} }} < 0,\,\frac{{\partial h^{{\text{L}}}_{{ut + 1}} }}{{\partial e_{{ut}} }} > 0,\,\frac{{\partial h^{{\text{H}}}_{{ut + 1}} }}{{\partial e_{{ut}} }} > 0$, and e _ut ^H′(p ^L)>0 if p ^L>p*, we can get that $\frac{{\partial H_{{ut + 1}} }} {{\partial p^{{\text{L}}} }} > 0$ from Eq. 41.

QED.