Abstract
Non-malleable codes (Dziembowski et al., ICS’10 and J. ACM’18) are a natural relaxation of error correcting/detecting codes with useful applications in cryptography. Informally, a code is non-malleable if an adversary trying to tamper with an encoding of a message can only leave it unchanged or modify it to the encoding of an unrelated value. This paper introduces continuous non-malleability, a generalization of standard non-malleability where the adversary is allowed to tamper continuously with the same encoding. This is in contrast to the standard definition of non-malleable codes, where the adversary can only tamper a single time. The only restriction is that after the first invalid codeword is ever generated, a special self-destruct mechanism is triggered and no further tampering is allowed; this restriction can easily be shown to be necessary. We focus on the split-state model, where an encoding consists of two parts and the tampering functions can be arbitrary as long as they act independently on each part. Our main contributions are outlined below.
-
We show that continuous non-malleability in the split-state model is impossible without relying on computational assumptions.
-
We construct a computationally secure split-state code satisfying continuous non-malleability in the common reference string (CRS) model. Our scheme can be instantiated assuming the existence of collision-resistant hash functions and (doubly enhanced) trapdoor permutations, but we also give concrete instantiations based on standard number-theoretic assumptions.
-
We revisit the application of non-malleable codes to protecting arbitrary cryptographic primitives against related-key attacks. Previous applications of non-malleable codes in this setting required perfect erasures and the adversary to be restricted in memory. We show that continuously non-malleable codes allow to avoid these restrictions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Physical attacks targeting cryptographic implementations instead of breaking the black-box security of the underlying algorithm are amongst the most severe threats for cryptographic systems. A particularly important attack on implementations is the so-called tampering attack, where the adversary changes the secret key to some related value and observes the effect of such changes at the output. Traditional black-box security notions do not incorporate adversaries that change the secret key to some related value; even worse, as shown in the celebrated work of Boneh et al. [22], already minor changes to the key suffice for complete security breaches. Unfortunately, tampering attacks are also rather easy to carry out: A virus corrupting a machine can gain partial control over the state, or an adversary that penetrates the cryptographic implementation with physical equipment may induce faults into keys stored in memory.
In recent years, a growing body of work (see [4, 11, 55, 64, 70, 76, 84]) developed new cryptographic techniques to tackle tampering attacks. Non-malleable codes introduced by Dziembowski, Pietrzak and Wichs [55, 56] are an important approach to achieve this goal. Intuitively a code is non-malleable w.r.t. a family of tampering functions \({\mathcal {F}}\) if the message contained in a codeword modified via a function \(f\in {\mathcal {F}}\) is either the original message, or a completely unrelated value. Non-malleable codes can be used to protect any cryptographic functionality against tampering with the memory. Instead of storing the key, we store its encoding and decode it each time the functionality wants to access the key. As long as the adversary can only apply tampering functions from the family \({\mathcal {F}}\), the non-malleability property guarantees that the (possibly tampered) decoded value is not related to the original key.
The standard notion of non-malleability considers a one-shot game: the adversary is allowed to tamper a single time with the codeword, after which it obtains the decoded output. In this work we introduce continuously non-malleable codes, where non-malleability is guaranteed even if the adversary continuously applies functions from the family \({\mathcal {F}}\) to the same codeword. We show that our new security notion is not only a natural extension of the standard definition, but moreover allows to protect against tampering attacks in important settings where earlier constructions fall short to achieve security.
1.1 Continuous Non-malleability
A code consists of two polynomial-time algorithms \(\Gamma = (\textsf {Enc},\textsf {Dec})\) satisfying the following correctness property: For all messages \(m\in {\mathcal {M}} \), it holds that \(\textsf {Dec}(\textsf {Enc}(m)) = m\) (with probability one over the randomness of the encoding). To define non-malleability for a function family \({\mathcal {F}}\), consider the following experiment \(\mathbf{Tamper} ^{\mathcal {F}}_{{\textsf {A}},\Gamma }(\lambda ,b)\) with hidden bit \(b\in \{0,1\}\) and featuring a (possibly unbounded) adversary \({\textsf {A}}\).
-
1.
The adversary chooses two messages \((m_0,m_1) \in {\mathcal {M}} ^2\).
-
2.
The challenger computes a target codeword
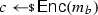 using the encoding procedure.
using the encoding procedure. -
3.
The adversary picks a tampering function \(f\in {\mathcal {F}}\), which yields a tampered codeword \(\tilde{c}= f(c)\). Hence:
-
If \(\tilde{c}= c\), then the attacker receives a special symbol \(\diamond \) denoting that tampering did not modify the target codeword;
-
Else, the adversary is given \(\textsf {Dec}(\tilde{c}) \in {\mathcal {M}} \cup \{\bot \}\), where \(\bot \) is a special symbol denoting that the tampered codeword \(\tilde{c}\) is invalid.
-
-
4.
The attacker outputs a guess \(b'\in \{0,1\}\).
A code \(\Gamma \) is said to be statistically (one-time) non-malleable w.r.t. \({\mathcal {F}}\) if for all attackers \(|{\mathbb {P}}\left[ b' = b\right] - 1/2|\) is negligible in the security parameter. This is equivalent to saying that the experiments \(\mathbf{Tamper} ^{\mathcal {F}}_{\Gamma ,{\textsf {A}}}(\lambda ,0)\) and \(\mathbf{Tamper} ^{{\mathcal {F}}}_{\Gamma ,{\textsf {A}}}(\lambda ,1)\) are statistically close. Computational non-malleability can be obtained by simply relaxing the above guarantee to computational indistinguishability (for all PPT adversaries).
To define continuously non-malleable codes, we allow the adversary to repeatFootnote 1 step 3 from the above game a polynomial number of times, where in each iteration the attacker can adaptively choose a tampering function \(f^{(i)} \in {\mathcal {F}}\). We emphasize that this change of the tampering game allows the adversary to tamper continuously with the target codeword \(c\). As shown by Gennaro et al. [70], such a strong security notion is impossible to achieve without further assumptions. To this end, we rely on the following self-destruct mechanism: Whenever in step 3 the experiment detects an invalid codeword and returns \(\bot \) for the first time, all future tampering queries will automatically be answered with \(\bot \). This is a rather mild assumption as it can, for instance, be implemented using a public, one-time writable, untamperable bit.
From non-malleable codes to tamper resilience As discussed above, the main application of non-malleable codes is to protecting cryptographic schemes against tampering with the secret key [55, 56, 84]. Consider a reactive functionality \(\textsf {F}\) with secret state \(\sigma \). Using a non-malleable code, earlier work showed how to transform the functionality \((\textsf {F},\sigma )\) into a so-called hardened functionality \((\hat{\textsf {F}},c)\) that is secure against memory tampering. The transformation works as follows: Initially, \(c\) is set to \(\textsf {Enc}(\sigma )\). Then, each time \(\hat{\textsf {F}}\) is executed on input x, the transformed functionality reads the encoding \(c\) from the memory, decodes it to obtain \(\sigma = \textsf {Dec}(c)\), and runs the original functionality \(\textsf {F}(\sigma ,x)\) obtaining an output y and a new state \(\sigma '\). Finally, it erases the memory and overwrites \(c\) with \(\textsf {Enc}(\sigma ')\).
Besides executing evaluation queries, the adversary can issue tampering queries \(f^{(i)} \in {\mathcal {F}}\). The effect of such a query is to overwrite the current codeword \(c\) stored in the memory with a tampered codeword \(\tilde{c}= f^{(i)}(c)\), so that the functionality \(\hat{\textsf {F}}\) will take \(\tilde{c}\) as input when answering the next evaluation query. The first time that \(\textsf {Dec}(\tilde{c}) = \bot \), the functionality \(\hat{\textsf {F}}\) sets the memory to a dummy value (which essentially results in a self-destruct).
The above transformation guarantees continuous tamper resilience even if the underlying non-malleable code is secure only against one-time tampering. This security “boost” is achieved by re-encoding the secret state after each execution of \(\hat{\textsf {F}}\). As one-time non-malleability suffices for the above cryptographic application, one may ask why we need continuously non-malleable codes. Besides being a natural generalization of the standard non-malleability notion, our new definition has several important advantages that we discuss in the next two paragraphs.
Tamper resilience without erasures The transformation described above necessarily requires that after each execution the entire content of the memory is erased. While such perfect erasures may be feasible in some settings, they are rather problematic in the presence of tampering. To illustrate this issue consider a setting where besides the encoding of a key, the memory also contains other non-encoded data. In the tampering setting, we cannot restrict the erasure to just the part that stores the encoding of the key as a tampering adversary may copy the encoding to some different part of the memory. A simple solution to this problem is to erase the entire memory, but such an approach is not possible in most cases: for instance, think of the memory as being the hard-disk of your computer that besides the encoding of a key stores other important files that you don’t want to be erased. Notice that this situation is quite different from the leakage setting, where we also require perfect erasures to achieve continuous leakage resilience. In the leakage setting, however, the adversary cannot mess around with the state of the memory by, e.g., copying an encoding of a secret key to some free space, which makes erasures significantly easier to implement.
One option to prevent the adversary from keeping permanent copies is to encode the entire state of the memory. Such an approach has, however, the following drawbacks.
-
It is unnatural In many cases, secret data, e.g., a cryptographic key, are stored together with non-confidential data. Each time we want to read some small part of the memory, e.g., the key, we need to decode and re-encode the entire state—including also the non-confidential data.
-
It is inefficient Decoding and re-encoding the entire state of the memory for each access introduces additional overhead and would result in highly inefficient solutions. This gets even worse as most current constructions of non-malleable codes are rather inefficient.
The second issue may be solved employing locally decodable and updatable non-malleable codes [42,43,44,45,46], which intuitively allow to access/update a portion of the message without reading/modifying the entire codeword. Using our new notion of continuously non-malleable codes we can avoid both issues in one go, and achieve continuous tamper resilience without using erasures or relying on inefficient solutions that encode the entire state.
Stateless tamper-resilient transformations To achieve tamper resistance from one-time non-malleability, we necessarily need to re-encode the state using fresh randomness. This not only reduces the efficiency of the proposed construction, but moreover makes the transformation stateful. Thanks to continuously non-malleable codes we get continuous security without the need to refresh the encoding after each usage. This is particularly useful when the underlying primitive that we want to protect is stateless itself (e.g., in the case of any standard block-cipher construction that typically keeps the same key). Using continuously non-malleable codes, the tamper-resilient implementation of such stateless primitives does not need to keep any secret state. We discuss the protection of stateless primitives in further detail in Sect. 5.
1.2 Our Contribution
Our main contribution is the first construction of continuously non-malleable codes in the split-state model, first introduced in the leakage setting [50, 54]. Various recent works study the split-state model for non-malleable codes [3, 4, 30, 53, 84] (see more details on related work in Sect. 1.3). In the split-state tampering model, the codeword consists of two halves \(c_0\) and \(c_1\) that are stored on two different parts of the memory. The adversary is assumed to tamper with both parts independently, but otherwise can apply any efficiently computable tampering function. That is, the adversary picks two polynomial-time computable functions \(f_0\) and \(f_1\) and replaces the codeword \((c_0,c_1)\) with \((f_0(c_0), f_1(c_1))\). Similar to the earlier work of Liu and Lysyanskaya [84], our construction assumes a public untamperable common reference string (CRS). Notice that this is a rather mild assumption, as the CRS can be hard-wired into the functionality and is independent of any secret data.
Continuous non-malleability of existing constructions The first construction of one-time split-state non-malleable codes (without random oracles) was given by Liu and Lysyanskaya [84]. At a high-level their construction encrypts the message \(m\) with a leakage-resilient encryption scheme, and generates a non-interactive zero-knowledge (NIZK) proof of knowledge showing that (i) the public/secret key of the PKE are valid, and (ii) the ciphertext is an encryption of \(m\) under the public key. Then, \(c_0\) is set to the secret key while \(c_1\) holds the corresponding public key, the ciphertext, and the NIZK proof.
Unfortunately, it is rather easy to break the non-malleable code of Liu and Lysyanskaya in the continuous setting. Recall that our security notion of continuously non-malleable codes allows the adversary to interact in the following game. First, we sample an encoding \(({\hat{c_{0}}},{\hat{c}_{1}})\) of \(m\), and then we repeat the following process a polynomial number of times.
-
1.
The adversary submits two polynomial-time computable functions \((f_0,f_1)\) resulting in a tampered codeword \((\tilde{c}_0,\tilde{c}_1) = (f_0({\hat{c}_{0}}), f_1({\hat{c}_{1}}))\).
-
2.
We consider three different cases:
-
If \((\tilde{c}_0,\tilde{c}_1) = ({\hat{c}_{0}},{\hat{c}_{1}})\), then return \(\diamond \).
-
Else, let \(\tilde{m}\) be the decoding of \((\tilde{c}_0,\tilde{c}_1)\). If \(\tilde{m}\ne \bot \), then return \(\tilde{m}\).
-
Else, if \(\tilde{m}= \bot \) self-destruct and terminate the experiment.
-
The main observation that enables the attack against the scheme of [84] is as follows: For a fixed (but adversarially chosen) part \(c_0\) it is easy to come up with two corresponding parts \(c_1\) and \(c_1'\) such that both \((c_0,c_1)\) and \((c_0,c_1')\) form a valid encoding (i.e., a codeword whose decoding does not yield \(\bot \)). Suppose further that decoding \((c_0,c_1)\) yields a message \(m\) that is different from the message \(m'\) obtained by decoding \((c_0,c_1')\). Then, under continuous tampering, the adversary may permanently replace the original encoding \({\hat{c}_{0}}\) with \(c_0\), while depending on whether the i-th bit of \({\hat{c}_{1}}\) being 0 or 1 either replace \({\hat{c}_{1}}\) by \(c_1\) or \(c_1'\). This allows to recover the entire \({\hat{c}_{1}}\) by just n tampering queries (where n is the size of \({\hat{c}_{1}}\)). Once \({\hat{c}_{1}}\) is known to the adversary, it is easyFootnote 2 to tamper with \({\hat{c}_{0}}\) in a way that depends on the message \({{\hat{m}}}\) corresponding to \(({\hat{c}_{0}},{\hat{c}_{1}})\).
Somewhat surprisingly, our attack can be generalized to break any non-malleable code that is secure in the information-theoretic setting. Hence, also the recent breakthrough results on information theoretic non-malleability [3,4,5, 53] fail to provide security under continuous attacks. Moreover, we emphasize that our attack does not only work for the code itself, but (in most cases) can be applied to the tamper-protection application of cryptographic functionalities.
Uniqueness The attack above exploits that for a fixed known part \(c_0\) it is easy to come up with two valid parts \(c_1,c_1'\). For the encoding of [84] this is indeed easy to achieve. If the secret key \(c_0\) is known, it is easy to come up with two valid parts \(c_1,c_1'\): just encrypt two arbitrary messages \(m,m'\) such that \(m\ne m'\), and generate the corresponding proofs. The above weakness motivates a new property that non-malleable codes shall satisfy in order to achieve continuous non-malleability. We call this property uniqueness, which informally guarantees that for any (adversarially chosen) valid encoding \((c_0,c_1)\) it be computationally hard to come up with \(c_1' \ne c_1\) such that \((c_0, c_{1}')\) forms a valid encoding.Footnote 3 Clearly, the uniqueness property prevents the above described attack, and hence is a crucial requirement for continuous non-malleability in the split-state model.
A new construction In light of the above discussion, we need to build a non-malleable code that achieves our uniqueness property. Our construction uses as building blocks a leakage-resilient storage (LRS) scheme [50, 52] for the split-state model (one may view this as a generalization of the leakage-resilient PKE used in [84]), a collision-resistant hash function, and (similar to [84]) an extractable NIZK. At a high-level we use the LRS to encode the secret message, hash the resulting shares using the hash function, and generate a NIZK proof of knowledge that indeed the resulting hash values are correctly computed from the shares. While it is easy to show that collision resistance of the hash function guarantees the uniqueness property, a careful analysis is required to prove continuous non-malleability. We refer the reader to Sect. 4.1 for the details of our construction, and to Sect. 4.2 for an outline of the proof.
Tamper resilience for stateless and stateful primitives We can use our new construction of continuously non-malleable codes to protect arbitrary computation against continuous tampering attacks. In contrast to earlier works, our construction does not need to re-encode the secret state after each usage, which besides being more efficient avoids the use of erasures. As discussed above, erasures are problematic in the tampering setting as one would essentially need to encode the entire state (possibly including large non-confidential data).
Additionally, our transformation does not need to keep any secret state. Hence, if our transformation is used to protect stateless primitives, then the resulting scheme remains stateless. This solves an open problem posed by Dziembowski, Pietrzak and Wichs [55, 56]. Notice that while we do not need to keep any secret state, the transformed functionality requires one bit of state to activate the self-destruct mechanism. This bit can be public, but must be untamperable, and can, for instance, be implemented through a one-time writable memory. As shown in the work of Gennaro et al. [70], continuous tamper resilience is impossible to achieve without such a mechanism for self-destruction.
Of course, our construction can also be used for stateful primitives, in which case our functionality will re-encode the new state during execution. Note that in our setting, where data are never erased, an adversary can always reset the functionality to a previous valid state. To avoid this, our transformation uses an untamperable public counterFootnote 4 that helps us detecting whenever the attacker tries to reset the functionality to a previous state (in which case, a self-destruct is triggered). We notice that such an untamperable counter is necessary, as otherwise there is no way to protect against the above resetting attack.Footnote 5
Bounded leakage resilience As an additional contribution, we show that our code is also secure against bounded leakage attacks. This is similar to the works of [53, 84] who also consider bounded leakage resilience of their encoding scheme. Furthermore, as we prove, bounded leakage resilience is also inherited by functionalities that are protected using our transformation.
Notice that without perfect erasures bounded leakage resilience is the best we can achieve, as there is no hope for security if an encoding that is produced at some point in time is gradually revealed to the adversary.
1.3 Related Work
Constructions of non-malleable codes Besides showing feasibility by a probabilistic argument, Dziembowski et al. [55, 56] also built non-malleable codes for bit-wise tampering (later improved in [9, 10, 32, 34, 36]) and gave a construction in the split-state model using a random oracle. This result was followed by [33], which proposed non-malleable codes that are secure against block-wise tampering. The first construction of non-malleable codes in the split-state model without random oracles was given by Liu and Lysyanskaya [84], in the computational setting, assuming an untamperable CRS. Several follow-up works focused on constructing split-state non-malleable codes in the information-theoretic setting [1, 3, 4, 7, 28, 53].
See also [9, 10, 12,13,14,15,16,17, 24, 25, 27, 31, 37, 45, 57, 64, 67, 77, 79,80,81,82] for other recent advances on the construction of non-malleable codes. We also notice that the work of Gennaro et al. [70] proposed a generic method that allows to protect arbitrary computation against continuous tampering attacks, without requiring erasures. We refer the reader to [55, 56] for a more detailed comparison between non-malleable codes and the solution of [70].
Other works on tamper resilience A large body of work shows how to protect specific cryptographic schemes against tampering attacks (see [18, 20, 21, 47, 48, 78, 86] and many more). While these works consider a strong tampering model (e.g., they do not require the split-state assumption), they only offer security for specific schemes. In contrast non-malleable codes are generally applicable and can provide tamper resilience of any cryptographic scheme.
In all the above works, including ours, it is assumed that the circuitry that computes the cryptographic algorithm using the potentially tampered key runs correctly, and is not subject to tampering attacks. An important line of works analyze to what extent we can guarantee security when even the circuitry is prone to tampering attacks [39, 40, 66, 69, 76, 83]. These works typically consider a restricted class of tampering attacks (e.g., individual bit tampering) and assume that large parts of the circuit (and memory) remain untampered.
Subsequent work A preliminary version of this paper appeared as [62]. Subsequent work showed that our impossibility result on information-theoretic continuous non-malleability can be circumvented in weaker tampering models, such as bit-wise tampering [34,35,36], high-min-entropy and few-fixed points tampering [77], 8-split-state tampering [6], permutations and overwrites [49], and space-bounded tampering [29, 61], or by assuming that the number of tampering queries is a priori fixed [26] and that tampering is persistent [8].
Continuously non-malleable codes have also been used to protect Random Access Machines against tampering attacks with the memory and the computation [63], and to obtain domain extension for non-malleable public-key encryption [34, 36, 49].
A recent work by Dachman-Soled and Kulkarni [41] shows that the strong flavor of continuous non-malleability in the split-state model considered in this paper (sometimes known as super non-malleability [64, 65]) is impossible to achieve in the plain model (i.e., without assuming an untamperable CRS). On the other hand, Ostrovsky et al. [85] proved that continuous weak non-malleability in the split-state model (i.e., the standard flavor of non-malleability in which the attacker only learns the output of the decoding corresponding to each tampered codeword) is possible in the plain model (assuming one-to-one one-way functions). Faonio and Venturi [58, 59] further consider continuously non-malleable split-state codes with a special refreshing procedure allowing to update codewords.
Finally, the concept of continuous non-malleability has also been recently studied in the more general setting of non-malleable secret sharing [23, 60, 71].
2 Preliminaries
2.1 Notation
For a string x, we denote its length by |x|; if \(\mathcal {X}\) is a set, \(|\mathcal {X}|\) represents the number of elements in \(\mathcal {X}\). When x is chosen randomly in \(\mathcal {X}\), we write  . When \(\textsf {A}\) is a randomized algorithm, we write
. When \(\textsf {A}\) is a randomized algorithm, we write  to denote a run of \(\textsf {A}\) on input x (and implicit random coins r) and output y; the value y is a random variable, and \(\textsf {A}(x;r)\) denotes a run of \(\textsf {A}\) on input x and randomness r. A randomized algorithm \(\textsf {A}\) is probabilistic polynomial-time (PPT) if for any input \(x,r\in \{0,1\}^*\) the computation of \(\textsf {A}(x;r)\) terminates in a polynomial number of steps (in the size of the input). For a PPT algorithm \(\textsf {A}\), we denote by \(\langle {\textsf {A}}\rangle \) its description using poly-many bits.
to denote a run of \(\textsf {A}\) on input x (and implicit random coins r) and output y; the value y is a random variable, and \(\textsf {A}(x;r)\) denotes a run of \(\textsf {A}\) on input x and randomness r. A randomized algorithm \(\textsf {A}\) is probabilistic polynomial-time (PPT) if for any input \(x,r\in \{0,1\}^*\) the computation of \(\textsf {A}(x;r)\) terminates in a polynomial number of steps (in the size of the input). For a PPT algorithm \(\textsf {A}\), we denote by \(\langle {\textsf {A}}\rangle \) its description using poly-many bits.
Negligible functions We denote with \(\lambda \in {\mathbb {N}}\) the security parameter. A function p is a polynomial, denoted \(p(\lambda )\in \texttt {poly}(\lambda )\), if \(p(\lambda )\in O(\lambda ^c)\) for some constant \(c>0\). A function \(\varepsilon :{\mathbb {N}}\rightarrow [0,1]\) is negligible in the security parameter (or simply negligible) if it vanishes faster than the inverse of any polynomial in \(\lambda \), i.e., \(\varepsilon (\lambda ) \in O(1/\lambda ^c)\) for every constant \(c > 0\). We often write \(\varepsilon (\lambda )\in \texttt {negl}(\lambda )\) to denote that \(\varepsilon (\lambda )\) is negligible.
Unless stated otherwise, throughout the paper, we implicitly assume that the security parameter is given as input (in unary) to all algorithms.
Random variables For a random variable \(\mathbf{X} \), we write \({\mathbb {P}}\left[ \mathbf{X} = x\right] \) for the probability that \(\mathbf{X} \) takes on a particular value \(x\in \mathcal {X}\) (with \(\mathcal {X}\) being the set where \(\mathbf{X} \) is defined). Given two ensembles  and
and  , we write \(\mathbf{X} {\mathop {\approx }\limits ^{\text {s}}}\mathbf{Y} \) (resp. \(\mathbf{X} {\mathop {\approx }\limits ^{\text {c}}}\mathbf{Y} \)) to denote that \(\mathbf{X} \) and \(\mathbf{Y} \) are statistically (resp. computationally) close, i.e., for all unbounded (resp. PPT) distinguishers \({\textsf {D}}\):
, we write \(\mathbf{X} {\mathop {\approx }\limits ^{\text {s}}}\mathbf{Y} \) (resp. \(\mathbf{X} {\mathop {\approx }\limits ^{\text {c}}}\mathbf{Y} \)) to denote that \(\mathbf{X} \) and \(\mathbf{Y} \) are statistically (resp. computationally) close, i.e., for all unbounded (resp. PPT) distinguishers \({\textsf {D}}\):
If the above distance is zero, we say that \(\mathbf{X} \) and \(\mathbf{Y} \) are identically distributed, denoted \(\mathbf{X} \equiv \mathbf{Y} \).
We extend the notion of computational indistinguishability to the case of interactive experiments (a.k.a. games) featuring an adversary \({\textsf {A}}\). In particular, let \(\mathbf{G} _{\textsf {A}}(\lambda )\) be the random variable corresponding to the output of \({\textsf {A}}\) at the end of the experiment, where \({\textsf {A}}\) outputs a decision bit. Given two experiments \(\mathbf{G} _{\textsf {A}}(\lambda ,0)\) and \(\mathbf{G} _{{\textsf {A}}}(\lambda ,1)\), we write  if for all PPT \({\textsf {A}}\) it holds that
if for all PPT \({\textsf {A}}\) it holds that
The above naturally generalizes to statistical distance (in case of unbounded adversaries).
2.2 Collision-Resistant Hashing
A family of hash functions \(\Pi :=(\textsf {Gen},\textsf {Hash})\) is a pair of efficient algorithms specified as follows: (i) The randomized algorithm \(\textsf {Gen}\) takes as input the security parameter and outputs a hash-key \(\textit{hk}\). (ii) The deterministic algorithm \(\textsf {Hash}\) takes as input the hash-key \(\textit{hk}\) and a value \(x\in \{0,1\}^*\), and outputs a value \(y\in \{0,1\}^\lambda \).
Definition 1
(Collision resistance) Let \(\Pi = (\textsf {Gen},\textsf {Hash})\) be a family of hash functions. We say that \(\Pi \) is collision resistant if for all PPT adversaries \({\textsf {A}}\) there exists a negligible function \(\nu :{\mathbb {N}}\rightarrow [0,1]\) such that:

2.3 Non-interactive Zero Knowledge
Let \(\mathcal {R}\) be an NP relation, corresponding to an NP language \({\mathcal {L}} \). A non-interactive argument system for \(\mathcal {R}\) is a tuple of efficient algorithms \(\Pi = (\textsf {CRSGen}, \textsf {Prove}, \textsf {Ver})\) specified as follows: (i) The randomized algorithm \(\textsf {CRSGen}\) takes as input the security parameter and outputs a common reference string \(\omega \); (ii) The randomized algorithm \(\textsf {Prove}(\omega ,\phi , (x, w))\), given \((x, w) \in \mathcal {R}\) and a label \(\phi \in \{0,1\}^*\), outputs an argument \(\pi \); (iii) The deterministic algorithm \(\textsf {Ver}(\omega ,\phi , (x, \pi ))\), given an instance \(x\), an argument \(\pi \), and a label \(\phi \in \{0,1\}^*\), outputs either 0 (for “reject”) or 1 (for “accept”). We say that \(\Pi \) is correct if for every \(\lambda \in {\mathbb {N}}\), all \(\omega \) as output by \(\textsf {CRSGen}(1^{\lambda })\), any label \(\phi \in \{0,1\}^*\), and any \((x,w) \in \mathcal {R}\), we have that \(\textsf {Ver}(\omega , \phi , (x, \textsf {Prove}(\omega , \phi , (x, w))))=1\) (with probability one over the randomness of the prover algorithm).
We define two properties of a non-interactive argument system. The first property says that honestly computed arguments do not reveal anything beyond the fact that \(x\in {\mathcal {L}} \).
Definition 2
(Adaptive multi-theorem zero-knowledge) A non-interactive argument system \(\Pi \) for a relation \(\mathcal {R}\) satisfies adaptive multi-theorem zero-knowledge if there exists a PPT simulator \(\textsf {S}:= (\textsf {S}_0,\textsf {S}_1)\) such that the following holds:
-
(i)
\(\textsf {S}_0\) outputs \(\omega \), a simulation trapdoor \(\zeta \) and an extraction trapdoor \(\xi \).
-
(ii)
For all PPT distinguishers \({\textsf {D}}\), we have that

is negligible in \(\lambda \), where the oracle \({\mathcal {O}} _\mathsf{sim}(\zeta ,\cdot ,(\cdot ,\cdot ))\) takes as input a tuple \((\phi ,(x,w))\) and returns \(\textsf {S}_1(\zeta ,\phi ,x)\) iff \((x,w)\in \mathcal {R}\) (and otherwise it returns \(\bot \)).
Groth [73] introduced the concept of simulation extractability, which informally states that knowledge soundness should hold even if the adversary can see simulated arguments for possibly false statements of its choice. For our purpose, it will suffice to consider the weaker notion of true-simulation extractability, as defined by Dodis et al. [51].
Definition 3
(True-simulation extractability) Let \(\Pi \) be a non-interactive argument system for a relation \(\mathcal {R}\), that satisfies adaptive multi-theorem zero-knowledge w.r.t. a simulator \(\textsf {S}:= (\textsf {S}_0,\textsf {S}_1)\). We say that \(\Pi \) is true-simulation extractable (tSE) if there exists a PPT algorithm \(\textsf {K}\) such that for all PPT adversaries \({\textsf {A}}\), it holds that

is negligible in \(\lambda \), where the oracle \({\mathcal {O}} _\mathsf{sim}(\zeta ,\cdot ,(\cdot ,\cdot ))\) takes as input a tuple \((\phi ,(x,w))\) and returns \(\textsf {S}_1(\zeta ,\phi ,x)\) iff \((x,w)\in \mathcal {R}\) (and otherwise it returns \(\bot \)), and the list \({\mathcal {Q}} \) contains all pairs \((\phi ,x)\) queried by \({\textsf {A}}\) to its oracle, along with the corresponding answer \(\pi \).
Note that the above definition allows the attacker to win using a pair label/statement \((\phi ^*,x^*)\) for which it already obtained a simulated argument, as long as the value \(\pi ^*\) is different from the argument \(\pi \) obtained from the oracle. This flavor is sometimes known as strong tSE, and it can be obtained generically from non-strong tSE (i.e., the attacker needs to win using a fresh pair \((\phi ^*,x^*)\)) using any strongly unforgeable one-time signature scheme [51].
2.4 Leakage-Resilient Storage
We recall the definition of leakage-resilient storage (LRS) from [50]. A leakage-resilient storage \(\Sigma = (\textsf {LREnc},\textsf {LRDec})\) is a pair of algorithms defined as follows: (i) The randomized algorithm \(\textsf {LREnc}\) takes as input message \(m\in \{0,1\}^k\) and outputs two shares \((s_0,s_1)\in \{0,1\}^{2n}\). (ii) The deterministic algorithm \(\textsf {LRDec}\) takes as input shares \((s_0,s_1)\in \{0,1\}^{2n}\) and outputs a value in \(\{0,1\}^k\). We say that \((\textsf {LREnc},\textsf {LRDec})\) satisfies correctness if for all \(m\in \{0,1\}^k\) it holds that \(\textsf {LRDec}(\textsf {LREnc}(m))=m\) (with probability 1 over the randomness of \(\textsf {LREnc}\)).
Security of LRS demands that, for any choice of messages \(m_0,m_1\in \{0,1\}^k\), it be hard for an attacker to distinguish bounded, independent, leakage from a target encoding of either \(m_0\) or \(m_1\). Below, we state such a property in the information-theoretic setting, as this flavor is met by known constructions. In what follows, for a leakage parameter \(\ell \in {\mathbb {N}}\), let \({\mathcal {O}}_\textsf {leak}^\ell (s,\cdot )\) be a stateful oracle taking as input functions \(g:\{0,1\}^n\rightarrow \{0,1\}^*\), and returning \(g(s)\) for a maximum of at most \(\ell \) bits.
Definition 4
(Leakage-resilient storage) We call \((\textsf {LREnc},\textsf {LRDec})\) an \(\ell \)-leakage-resilient storage (\(\ell \)-LRS for short) if it holds that
where for \({\textsf {A}}:= ({\textsf {A}}_0,{\textsf {A}}_1)\) and \(b\in \{0,1\}\) we set:

For our construction, we will need a slight variant of the above definition where at the end of the game the attacker is further allowed to obtain one of the two shares in full. Following [2], we refer to this variant as augmented LRS.
Definition 5
(Augmented leakage-resilient storage) We call \((\textsf {LREnc},\textsf {LRDec})\) an augmented \(\ell \)-LRS if for all \(\sigma \in \{0,1\}\) it holds that
where for \({\textsf {A}}= ({\textsf {A}}_0,{\textsf {A}}_1,{\textsf {A}}_2)\) and \(b\in \{0,1\}\) we set:

The lemma belowFootnote 6 shows the equivalence between Definitions 5 and 4 up to a loss of a single bit in the leakage parameter.
Theorem 1
Let \(\Sigma = (\textsf {LREnc},\textsf {LRDec})\) be an \(\ell \)-LRS. Then, \(\Sigma \) is an augmented \((\ell -1)\)-LRS.
Proof
We prove the lemma by contradiction. Assume that there exists some adversary \({\textsf {A}}^{+} = ({\textsf {A}}^{+}_0,{\textsf {A}}^{+}_1,{\textsf {A}}^{+}_2)\) able to distinguish with non-negligible probability between \(\mathbf{Leak} ^{+}_{\Sigma ,{\textsf {A}}^{+}}(\lambda ,0,\sigma )\) and \(\mathbf{Leak} ^{+}_{\Sigma ,{\textsf {A}}^{+}}(\lambda ,1,\sigma )\) for some fixed \(\sigma \in \{0,1\}\) and using \(\ell -1\) bits of leakage. We construct another adversary \({\textsf {A}}= ({\textsf {A}}_0,{\textsf {A}}_1)\) which can distinguish between \(\mathbf{Leak} _{\Sigma ,{\textsf {A}}}(\lambda ,0)\) and \(\mathbf{Leak} _{\Sigma ,{\textsf {A}}}(\lambda ,1)\) with the same distinguishing advantage, using \(\ell \) bits of leakage. A description of \({\textsf {A}}\) follows:
\(\underline{\hbox {Adversary }{\textsf {A}}:}\)
\({\textsf {A}}_0\) simply runs \({\textsf {A}}_0^{+}(1^\lambda )\) and returns its output \((m_0,m_1,\alpha _1)\).
\({\textsf {A}}_1\) first runs \({\textsf {A}}_1^{+}(1^\lambda ,\alpha _1)\) by simply forwarding its leakage queries to its own target left/right leakage oracle.
Denote by \(\alpha _2\) the output of \({\textsf {A}}_1^{+}\), and let \({\hat{g}}^{{\textsf {A}}_2^{+},\alpha _2}_{\sigma }\) be the leakage function that hard-wires (a description of) \({\textsf {A}}_2^{+}\) and the auxiliary information \(\alpha _2\), and upon input \(s_\sigma \) returns the same as \({\textsf {A}}_2^{+}(1^\lambda ,\alpha _2,s_\sigma )\).
\({\textsf {A}}_1\) forward \({\hat{g}}^{{\textsf {A}}_2^{+},\alpha _2}_{\sigma }\) to the leakage oracle \({\mathcal {O}}_\textsf {leak}^\ell (s_\sigma ,\cdot )\) obtaining a bit \(b'\), and finally outputs \(b'\) as its guess.
It is clear that \({\textsf {A}}\) leaks at most \(\ell -1+1=\ell \) bits. Moreover, \({\textsf {A}}\) perfectly simulates the view of \({\textsf {A}}^{+}\), and thus, it retains the same advantage. This finishes the proof. \(\square \)
3 Continuous Non-Malleability
In this section, we formalize the notion of continuous non-malleability against split-state tampering in the common reference string (CRS) model. To that end, we start by describing the syntax of split-state codes in the CRS model.
Formally, a split-state code in the CRS model is a tuple of algorithms \(\Gamma = (\textsf {Init},\textsf {Enc},\textsf {Dec})\) specified as follows: (i) The randomized algorithm \(\textsf {Init}\) takes as input the security parameter and outputs a CRS  . (ii) The randomized encoding algorithm \(\textsf {Enc}\) takes as input some message \(m\in \{0,1\}^{k}\) and the CRS, and outputs a codeword consisting of two parts \(c:= (c_0,c_1)\in \{0,1\}^{2n}\) where \(c_0,c_1\in \{0,1\}^n\). (iii) The deterministic algorithm \(\textsf {Dec}\) takes as input a codeword \((c_0,c_1)\in \{0,1\}^{2n}\) and the CRS, and outputs either a message \(m'\in \{0,1\}^{k}\) or a special symbol \(\bot \).
. (ii) The randomized encoding algorithm \(\textsf {Enc}\) takes as input some message \(m\in \{0,1\}^{k}\) and the CRS, and outputs a codeword consisting of two parts \(c:= (c_0,c_1)\in \{0,1\}^{2n}\) where \(c_0,c_1\in \{0,1\}^n\). (iii) The deterministic algorithm \(\textsf {Dec}\) takes as input a codeword \((c_0,c_1)\in \{0,1\}^{2n}\) and the CRS, and outputs either a message \(m'\in \{0,1\}^{k}\) or a special symbol \(\bot \).
As usual, we say that \(\Gamma \) is correct if for all \(\lambda \in {\mathbb {N}}\), for all \(\omega \in \textsf {Init}(1^\lambda )\), and for all \(m\in \{0,1\}^k\), it holds that \(\textsf {Dec}(\omega ,\textsf {Enc}(\omega ,m))=m\) (with probability 1 over the randomness of \(\textsf {Enc}\)).
3.1 The Definition
Intuitively, non-malleability captures a setting where an adversary \({\textsf {A}}\) tampers a single time with a target encoding \(c:= (c_0,c_1)\) of some message \(m\). The tampering attack is arbitrary, as long as it modifies the two parts \(c_0\) and \(c_1\) of the target codeword \(c\) independently, i.e., the attacker can choose any tampering function \(f:= (f_0,f_1)\) where \(f_0,f_1:\{0,1\}^n\rightarrow \{0,1\}^n\). This results in a modified codeword \(\tilde{c} := (\tilde{c}_0,\tilde{c}_1) := (f_0(c_0),f_1(c_1))\), and different flavors of non-malleability are possible depending on what information the attacker obtains about the decoding of \(\tilde{c}\):
-
Weak non-malleability In this case the attacker obtains the decoded message \(\tilde{m}\in \{0,1\}^k\cup \{\bot \}\) corresponding to \(\tilde{c}\), unless \(\tilde{m} = m\) (in which case the adversary gets a special “same” symbol \(\diamond \));
-
Strong non-malleability In this case the attacker obtains the decoded message \(\tilde{m}\in \{0,1\}^k\cup \{\bot \}\) corresponding to \(\tilde{c}\), unless \(\tilde{c} = c\) (in which case the adversary gets a special “same” symbol \(\diamond \));
-
Super non-malleability In this case the attacker obtains \(\tilde{c}\), unless \(\tilde{c}\) is invalid (in which case the adversary gets \(\bot \)), or \(\tilde{c} = c\) (in which case the adversary gets a special “same” symbol \(\diamond \)).
Super non-malleability is the strongest flavor, as it implies that not even the mauled codeword reveals information about the underlying message (as long as it is valid and different from the original codeword). Similarly, one can see that strong non-malleability is strictly stronger than weak non-malleability. For the rest of this paper, whenever we write “non-malleability” (without specifying the flavor weak/strong/super) we implicitly mean “super non-malleability”.
Continuous non-malleability generalizes the above setting to the case where the attacker tampers adaptively with the same target codeword \(c\), and for each attempt obtains some information about the decoding of the modified codeword \(\tilde{c}\) (as above). The only restriction is that whenever a tampering attempt yields an invalid codeword, the system “self-destructs”. Toward defining continuous non-malleability, consider the following oracle \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),\cdot )\), which is parameterized by a codeword \((c_0,c_1)\) and takes as input functions \(f_{0},f_{1}:\{0,1\}^{n}\rightarrow \{0,1\}^{n}\).
\(\underline{\hbox {Oracle }{\mathcal {O}}_\mathsf{maul}((c_0,c_1),(f_{0},f_{1}))}:\)
\((\tilde{c}_0,\tilde{c}_1) = (f_{0}(c_0),f_{1}(c_1))\)
If \((\tilde{c}_0,\tilde{c}_1) = (c_0,c_1)\) return \(\diamond \)
If \(\textsf {Dec}(\omega ,(\tilde{c}_0,\tilde{c}_1)) = \bot \), return \(\bot \) and “self-destruct”
Else return \((\tilde{c}_0,\tilde{c}_1)\).
By “self-destruct” we mean that once \(\textsf {Dec}(\omega ,(\tilde{c}_0,\tilde{c}_1))\) outputs \(\bot \), the oracle will answer \(\bot \) to any further query. We are now ready to define (leakage-resilient) continuous non-malleability.
Definition 6
(Continuous non-malleability) Let \(\Gamma = (\textsf {Init},\textsf {Enc},\textsf {Dec})\) be a split-state code in the CRS model. We say that \(\Gamma \) is \(\ell \)-leakage-resilient continuously super-non-malleable (\(\ell \)-CNMLR for short), if it holds that
where for \({\textsf {A}}:= ({\textsf {A}}_0,{\textsf {A}}_1)\) and \(b\in \{0,1\}\) we set:

3.2 Codewords Uniqueness
As we argue below, constructions that satisfy our new Definition 6 have to meet the following requirement: For any (possibly adversarially chosen) side of an encoding \(c_0\) it is computationally hard to find two corresponding sides \(c_{1}\) and \(c_{1}'\) such that both \((c_0,c_{1})\) and \((c_0,c_{1}')\) form a valid encoding; moreover, a similar property holds if we fix the right side \(c_1\) of a codeword.
Definition 7
(Codewords uniqueness) Let \(\Gamma = (\textsf {Init},\textsf {Enc},\textsf {Dec})\) be a split-state code in the CRS model. We say that \(\Gamma \) satisfies codewords uniqueness if for all PPT adversaries \({\textsf {A}}\) we have:

The following attack shows that codewords uniqueness is necessary to achieve Definition 6.
Lemma 1
Let \(\Gamma \) be a 0-leakage-resilient continuously super-non-malleable split-state code. Then, \(\Gamma \) must satisfy codewords uniqueness.
Proof
For the sake of contradiction, assume that there exists a PPT attacker \({\textsf {A}}'\) that outputs a triple \((c_0,c_1,c_1')\) violating uniqueness of \(\Gamma \), i.e., such that \((c_0,c_{1})\) and \((c_0,c_{1}')\) are both valid, with \(c_1 \ne c_1'\). We show how to construct a PPT attacker \({\textsf {A}}:= ({\textsf {A}}_0,{\textsf {A}}_1)\) breaking continuous non-malleability of \(\Gamma \). Attacker \({\textsf {A}}_0\), given the CRS, outputs any two messages \(m_0,m_1\in \{0,1\}^k\) which differ, say, in the first bit; denote by \(({\hat{c}_{0}},{\hat{c}_{1}})\) the target codeword corresponding to \(m_b\) in the experiment \(\mathbf{Tamper} _{\Gamma ,{\textsf {A}}}(\lambda ,b)\). Attacker \({\textsf {A}}_1\) runs \({\textsf {A}}'\), and then queries the tampering oracle \({\mathcal {O}}_\mathsf{maul}(({\hat{c}_{0}},{\hat{c}_{1}}),\cdot )\) with a sequence of \(n\in \texttt {poly}(\lambda )\) tampering queries, where the i-th query \((f_0^{(i)},f_1^{(i)})\) is specified as follows:
-
Function \(f_0^{(i)}\) overwrites \({\hat{c}_{0}}\) with \(c_0\).
-
Function \(f_1^{(i)}\) reads the i-th bit \({\hat{c}_{1}}[i]\) of \({\hat{c}_{1}}\); in case \({\hat{c[i]}}=0\) it overwrites \({\hat{c}_{1}}\) with \(c_1\), and else it overwrites \({\hat{c}_{1}}\) with \(c_1'\).
Note that, as long as \({\textsf {A}}'\) breaks codewords uniqueness, \(\tilde{c}^{(i)} = (f_0^{(i)}(c_0),f_1^{(i)}(c_1))\) is a valid codeword for all \(i\in [n]\). This allows \({\textsf {A}}_1\) to fully recover \({\hat{c}_{1}}\) after \(n\) tampering queries, unless \(({\hat{c}_{0}},{\hat{c}_{1}})\in \{(c_0,c_1),(c_0,c_1')\}\).Footnote 7
Finally, \({\textsf {A}}_1\) asks an additional tampering query \((f_{0}^{(n+1)},f_{1}^{(n+1)})\) to \({\mathcal {O}}_\mathsf{maul}(({\hat{c}_{0}},{\hat{c}_{1}}),\cdot )\):
-
\(f_{0}^{(n+1)}({\hat{c}_{0}})\) hard-wires \({\hat{c}_{1}}\) and computes \(m= \textsf {Dec}(\omega ,({\hat{c}_{0}},{\hat{c}_{1}}))\); if the first bit of \(m\) is 0, then it behaves like the identity function, and otherwise it overwrites \({\hat{c}_{0}}\) with \(0^n\).
-
\(f_{1}^{(n+1)}({\hat{c}_{1}})\) is the identity function.
The above clearly allows to learn the first bit of the message in the target encoding, and hence contradicts the fact that \(\Gamma \) is continuously non-malleable. \(\square \)
Attacking existing schemes The attack of Lemma 1 can be used to show that the code of [84] does not satisfy continuous non-malleability as per our definition. Recall that in [84] a message \(m\) is encoded as \(c_0 = (\textit{pk},\gamma :=\textsf {Encrypt}(\textit{pk},m), \pi )\) and \(c_1 = \textit{sk}\). Here, \((\textit{pk},\textit{sk})\) is a valid public/secret key pair and \(\pi \) is an argument of knowledge of \((m,\textit{sk})\) such that \(\gamma \) decrypts to \(m\) under \(\textit{sk}\) and \((\textit{pk},\textit{sk})\) is well formed. Clearly, for any fixed \(c_1 = \textit{sk}\) it is easy to find two corresponding parts \(c_0 \ne c_0'\) such that both \((c_0,c_1)\) and \((c_0',c_1)\) are valid.Footnote 8
Let us mention two important extensions of the above attack, leading to even stronger security breaches.
-
1.
In case the pair of valid codewords \((c_0,c_1)\), \((c_0,c'_1)\) violating the uniqueness property are such that \(\textsf {Dec}(\omega ,(c_0,c_1)) \ne \textsf {Dec}(\omega ,(c_0,c'_1))\), one can show that Lemma 1 even rules out continuous weak non-malleability.Footnote 9 The latter flavor of uniqueness is sometimes referred to as message uniqueness [60, 85].
-
2.
In case it is possible to find both \((c_0,c_1,c'_1)\) and \((c_0,c'_0,c_1)\) violating uniqueness, a simple variant of the attack from Lemma 1 allows to recover both halves of the target encoding, which is a total breach of security. However, it is not clear how to do that for the scheme of [84], as once we fix \(c_0 = (\textit{pk},\gamma ,\pi )\), it shall be hard to find two valid secret keys \(c_1 = \textit{sk}\ne \textit{sk}' = c_1'\) corresponding to \(\textit{pk}\).
A simple adaptation of the above attack shows that continuous non-malleability in the split-state model is impossible in the information-theoretic setting.
Theorem 2
There is no split-state code \(\Gamma \) in the CRS model that is 0-leakage-resilient continuously super-non-malleable in the presence of a computationally unbounded adversary.
Proof
By contradiction, assume that there exists an information-theoretically secure continuously non-malleable split-state code \(\Gamma \) with \(2n\)-bit codewords. By Lemma 1, the code \(\Gamma \) must satisfy codewords uniqueness. In the information-theoretic setting, this means that for all CRSs \(\omega \in \textsf {Init}(1^\lambda )\), and for any codeword \((c_0,c_1)\in \{0,1\}^{2n}\) such that \(\textsf {Dec}(\omega ,(c_0,c_1))\ne \bot \), the following two properties hold: (i) for all \(c'_1\in \{0,1\}^{n}\) such that \(c'_1\ne c_1\), we have \(\textsf {Dec}(\omega ,(c_0,c'_1)) = \bot \); (ii) for all \(c'_0\in \{0,1\}^{n}\) such that \(c'_0\ne c_0\), we have \(\textsf {Dec}(\omega ,(c'_0,c_1)) = \bot \).
Let now \(({\hat{c}}_0,{\hat{c}}_1)\) be a target encoding of some secret \(m\in \{0,1\}^k\). An unbounded attacker \({\textsf {A}}\) can define the following tampering query \((f_0,f_1)\):
-
\(f_0\), given \({\hat{c}_{0}}\) as input, tries all possible \({\hat{c}_{1}}\in \{0,1\}^{n}\) until one is found such that \(\textsf {Dec}(\omega ,({\hat{c}_{0}},{\hat{c}_{1}})) \ne \bot \). Hence, it runs \(m= \textsf {Dec}(\omega ,({\hat{c}_{0}},{\hat{c}_{1}}))\), and it leaves \({\hat{c}}_0\) in case the first bit of the message is zero whereas it overwrites \({\hat{c}_{0}}\) with \(0^n\) otherwise.
-
\(f_{1}\) is the identity function.
Note that by properties (i) and (ii) above, we know that for all \({{\hat{c}}}'_{1} \ne {\hat{c}_{1}}\), the decoding algorithm \(\textsf {Dec}(\omega ,({\hat{c}_{0}},{\hat{c}_{1}}'))\) outputs \(\bot \). Thus, the above tampering query allows to learn the first bit of \(m\) with overwhelming probability, which is a clear breach of non-malleability.
\(\square \)
Note that although the attack of Theorem 2 uses a single (inefficient) tampering query, it crucially relies on the assumption that the code \(\Gamma \) be continuously non-malleable, in that it uses the fact that \(\Gamma \) satisfies codewords uniqueness. This is consistent with the fact that all split-state codes that achieve one-time non-malleability in the information-theoretic setting do not satisfy uniqueness.
4 The Code
We describe our split-state code in Sect. 4.1. A detailed outline of the security proof can be found in Sect. 4.2, whereas the formal proof is given in Sect. 4.3–4.5 Finally, in Sect. 4.6, we explain how to instantiate our scheme both from generic and concrete assumptions.
4.1 Description
Our construction combines a hash function \((\textsf {Gen}, \textsf {Hash})\) (cf. Sect. 2.2), a non-interactive argument system \((\textsf {CRSGen},\textsf {Prove},\textsf {Ver})\) for proving knowledge of a pre-image of a hash value (cf. Sect. 2.3), and a leakage-resilient storage \(\Sigma = (\textsf {LREnc},\textsf {LRDec})\) (cf. Sect. 2.4), as depicted in Fig. 1.
The main idea behind the scheme is as follows: The CRS includes the CRS \(\omega \) for the argument system and the hash key \(\textit{hk}\) for the hash function. Given a message \(m\in \{0,1\}^k\), the encoding procedure first encodes \(m\) using \(\textsf {LREnc}\), obtaining shares \((s_0,s_1)\). Hence, it hashes both \(s_0\) and \(s_1\), obtaining values \(h_0\) and \(h_1\), and generates a non-interactive argument \(\pi _0\) (resp. \(\pi _1\)) for the statement \(h_0\in {\mathcal {L}} _\mathsf{hash}^{\textit{hk}}\) (resp. \(h_1\in {\mathcal {L}} _\mathsf{hash}^{\textit{hk}}\)) using \(h_1\) (resp. \(h_0\)) as label. The left part \(c_0\) (resp. right part \(c_1\)) of the codeword \(c^*\) consists of \(s_0\) (resp. \(s_1\)), along with the value \(h_1\) (resp. \(h_0\)), and with the arguments \(\pi _0,\pi _1\).
The decoding algorithm proceeds in the natural way. Namely, given a codeword \(c^* = (c_0,c_1)\) it first checks that the arguments contained in the left and right part are equal, and moreover that the hash values are consistent with the shares; further, it checks that the non-interactive arguments verify correctly w.r.t. the corresponding statement and label. If any of the above checks fails, the algorithm returns \(\bot \), and otherwise it outputs the same as \(\textsf {LRDec}(s_0,s_1)\).
Correctness of the code \(\Gamma ^*\) follows directly by the correctness properties of the LRS and of the non-interactive argument system. As for security, we establish the following result.
Theorem 3
Let \(\ell \in {\mathbb {N}}\). Assume that:
-
(i)
\((\textsf {LREnc},\textsf {LRDec})\) is an augmented \(\ell \)-leakage-resilient storage;
-
(ii)
\((\textsf {Gen},\textsf {Hash})\) is a collision-resistant hash function;
-
(iii)
\((\textsf {CRSGen},\textsf {Prove},\textsf {Ver})\) is a true-simulation extractable non-interactive zero-knowledge argument system for the language \({\mathcal {L}} _\mathsf{hash}^{\textit{hk}} = \{h\in \{0,1\}^\lambda :\exists s\in \{0,1\}^n\text { s.t. }\textsf {Hash}(\textit{hk},s)=h\}\).
Then, the split-state code \(\Gamma ^*\) described in Fig. 1 is an \(\ell ^*\)-leakage-resilient continuously super-non-malleable code in the CRS model, as long as \(\ell ^* \le \ell /2 - O(\lambda \log (\lambda ))\).
4.2 Proof Outline
Our goal is to show that no PPT attacker \({\textsf {A}}^*\) can distinguish the experiments \(\mathbf{Tamper} _{\Gamma ^*,{\textsf {A}}^*}(\lambda ,0)\) and \(\mathbf{Tamper} _{\Gamma ^*,{\textsf {A}}^*}(\lambda ,1)\) (cf. Definition 6). Recall that \({\textsf {A}}^*\), after seeing the CRS, can select two messages \(m_0,m_1\in \{0,1\}^k\), and then adaptively tamper with, and leak from, a target encoding \(c^* = (c_0,c_1)\) of either \(m_0\) or \(m_1\), where both the tampering and the leakage act independently on the two parts \(c_0\) and \(c_1\).
Modified tampering oracle \({\mathcal {O}}_\mathsf{maul}'\) used in the experiment \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^2(\lambda , b)\). For simplicity, we assume that the extractor \(\textsf {K}\) is deterministic (which is the case for known instantiations, e.g., [51]); a generalization is immediate
In order to prove the theorem, we introduce two hybrid experiments, as outlined below.
- \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^1(\lambda ,b)\)::
-
In the first hybrid, we modify the distribution of the target codeword \(c^* = (c_0,c_1)\). In particular, we first use the simulator \(\textsf {S}_0\) of the non-interactive argument system to program the CRS \(\omega \), yielding simulation trapdoor \(\zeta \) and extraction trapdoor \(\xi \), and then we compute the argument \(\pi _0\) (resp. \(\pi _1\)) by running the simulator \(\textsf {S}_1\) upon input \(\zeta \), statement \(h_0\) (resp. \(h_1\)) and label \(h_1\) (resp. \(h_0\)).
- \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^2(\lambda ,b)\)::
-
In the second hybrid, we modify the way tampering queries are answered. In particular, let \((f_0,f_1)\) be a generic tampering query, and \(\tilde{c}^* = (\tilde{c}_0,\tilde{c}_1) = (f_0(c_0),f_1(c_1))\) be the corresponding mauled codeword. Note that \(\tilde{c}_0\) can be parsed as \(\tilde{c}_0 = (\tilde{s}_0, \tilde{h}_1, \tilde{\pi }_{0,0},\tilde{\pi }_{1,0})\), and similarly \(\tilde{c}_1 = (\tilde{s}_1, \tilde{h}_{0}, \tilde{\pi }_{0,1},\tilde{\pi }_{1,1})\). The modified tampering oracle then proceeds as follows, for each \(\beta \in \{0,1\}\).
- (a):
-
In case \(\tilde{c}_\beta = c_\beta \), define \(\Theta _\beta := \diamond \) (cf. Type-A queries in Fig. 2).
- (b):
-
In case \(\tilde{c}_\beta \ne c_\beta \), but either of the arguments in \(\tilde{c}_\beta \) does not verify correctly, define \(\Theta _\beta := \bot \) (cf. Type-B queries in Fig. 2).
- (c):
-
In case \(\tilde{c}_\beta \ne c_\beta \) and both the arguments in \(\tilde{c}_\beta \) verify correctly, let \(\tilde{h}_{\beta ,\beta } := \textsf {Hash}(\textit{hk},\tilde{s}_\beta )\). Check if \((\tilde{h}_{1-\beta },\tilde{h}_{\beta ,\beta },\tilde{\pi }_{1-\beta ,\beta }) = (h_{1-\beta },h_{\beta },\pi _{1-\beta })\); if not (in which case we cannot extract from \(\tilde{\pi }_{1-\beta }\)), then define \(\Theta _\beta := \bot \) (cf. Type-C queries in Fig. 2).
- (d):
-
Otherwise, run the knowledge extractor \(\textsf {K}\) of the underlying non-interactive argument system upon input extraction trapdoor \(\xi \), statement \(\tilde{h}_{1-\beta }\), argument \(\tilde{\pi }_{1-\beta ,\beta }\), and label \(\tilde{h}_{\beta ,\beta } := \textsf {Hash}(\textit{hk},\tilde{s}_\beta )\), yielding a share \(\tilde{s}_{1-\beta }\). Thus, let \(\tilde{c}_{1-\beta } = (\tilde{s}_{1-\beta },\tilde{h}_{\beta ,\beta },\tilde{\pi }_{0,\beta },\tilde{\pi }_{1,\beta })\) and define \(\Theta _\beta := (\tilde{c}_0,\tilde{c}_1)\) (cf. Type-D queries in Fig. 2).
Finally, if \(\Theta _0 = \Theta _1\) the oracle returns this value as answer to the tampering query \((f_0,f_1)\); else, it returns \(\bot \) and self-destructs. (Of course, in case \(\Theta _0 = \Theta _1 = \bot \), the oracle also returns \(\bot \) and self-destructs.)
As a first step, we argue that \(\mathbf{Tamper} _{\Gamma ^*, {\textsf {A}}^*}(\lambda ,b)\) and \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^1(\lambda ,b)\) are computationally close. This follows readily from adaptive multi-theorem zero knowledge of the non-interactive argument system, as the only difference between the two experiments is the fact that in the latter the arguments \(\pi _0,\pi _1\) are simulated. As a second step, we prove that \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^1(\lambda ,b)\) and \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}}^2(\lambda ,b)\) are also computationally indistinguishable. More in details, we show how to bound the probability that the output of the tampering oracle in the two experiments differs in the above described cases (a), (b), (c) and (d):
-
(a)
For Type-A queries, note that when \(\tilde{c}_\beta = c_\beta \), we must have \(\tilde{c}_{1-\beta } = c_{1-\beta }\) with overwhelming probability, as otherwise, say, \((c_0,c_1,\tilde{c}_1)\) would violate codewords uniqueness, which for our code readily follows from collision resistance of the hash function.
-
(b)
For Type-B queries, the decoding process in the previous hybrid would also return \(\bot \), so these queries always yield the same output in the two experiments.
-
(c)
For Type-C queries, we use the facts that (i) the underlying non-interactive argument system is true-simulation extractable, and (ii) the hash function is collision resistant, to show that \(\tilde{c}_\beta \) must be of the form \(\tilde{c}_\beta = (s_\beta ,h_{1-\beta },\tilde{\pi }_{0,\beta },\pi _{1,\beta })\) with \(\tilde{\pi }_{0,\beta } \ne \pi _{1,\beta }\). As we show, the latter contradicts security of the underlying LRS.
-
(d)
For Type-D queries, note that whenever we run the extractor either the statement \(\tilde{h}_{1-\beta }\), or the argument \(\tilde{\pi }_{1-\beta ,\beta }\), or the label \(\tilde{h}_{\beta ,\beta }\) are fresh, which ensures the witness must be valid with overwhelming probability by (true-simulation) extractability of the non-interactive argument system.
Next, we show that no PPT attacker \({\textsf {A}}^*\) can distinguish between experiments \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^2(\lambda ,0)\) and \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^2(\lambda ,1)\) with better than negligible probability. To this end, we build a reduction \({\textsf {A}}\) to the security of the underlying LRS. In order to keep the exposition simple, let us first assume that \({\textsf {A}}^*\) is not allowed to ask leakage queries. Roughly, the reduction works as follows:
-
Simulate the CRS: At the beginning, \({\textsf {A}}\) samples a programmed CRS \(\omega \) and the hash key \(\textit{hk}\) exactly as defined in \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^2(\lambda ,b)\), and runs \({\textsf {A}}^*\) upon \(\omega ^* := (\omega ,\textit{hk})\) and fresh randomness r. Upon receiving \((m_0,m_1)\) from \({\textsf {A}}^*\), then \({\textsf {A}}\) forward the same pair of messages to the challenger.
-
Learn the self-destruct index: Note that in the last hybrid, the tampering oracle answers \({\textsf {A}}^*\)’s tampering queries by computing both \(\Theta _0\) (looking only at \(c_0\)) and \(\Theta _1\) (looking only at \(c_1\)), and then \(\Theta _0\) is returned as long as \(\Theta _0 = \Theta _1\) (and otherwise a self-destruct is triggered). Since \({\textsf {A}}\) can leak independently from \(s_0\) and \(s_1\), it can compute all the values \(\Theta _\beta \) by running \({\textsf {A}}^*\) with hard-wiredFootnote 10 randomness r insideFootnote 11 each of its leakage oracles, and then use a pairwise independent hash function to determine using a binary search the first index \(i^*\) corresponding to the tampering query where \(\Theta _0 \ne \Theta _1\). By pairwise independence, this yields the index of the query \(i^*\) in which \({\textsf {A}}^*\) provokes a self-destruct with overwhelming probability, and by leaking at most \(O(\lambda \log \lambda )\) bits from each block.
-
Play the game: Once the self-destruct index \(i^*\) is known, \({\textsf {A}}\) obtainsFootnote 12\(s_\sigma \) and can thus restart \({\textsf {A}}^*\) outside the leakage oracle, using the same randomness r, and answer to the first \(i^*-1\) tampering queries using \(c_\sigma = (s_\sigma ,h_{1-\sigma },\pi _{0},\pi _{1})\), after which the answer to all remaining tampering queries is set to be \(\bot \). This yields a perfect simulation of how tampering queries are handled in the last hybrid, so that \({\textsf {A}}\) keeps the advantage of \({\textsf {A}}^*\).
Finally, let us explain how to remove the simplifying assumption that \({\textsf {A}}^*\) cannot leak from the target codeword. The difficulty when considering leakage is that we cannot run anymore the entire experiment with \({\textsf {A}}^*\) inside the leakage oracle, as the answer to \({\textsf {A}}^*\)’s leakage queries depends on the other half of the target codeword. However, note that in this case we can stop the execution and inform the reduction to leak from the other side whatever information is needed to continue the execution of each copy of \({\textsf {A}}^*\) inside the leakage oracle.
This allows to obtain the answers to all leakage queries of \({\textsf {A}}^*\) up to a self-destruct occurs. In order to obtain the answers to the remaining queries, we must re-run \({\textsf {A}}\) inside the leakage oracle and adjust the simulation consistently with the self-destruct index being \(i^*\). In the worst case, this requires \(2\ell ^*\) bits of leakage, yielding the final bound of \(2\ell ^* + O(\lambda \log \lambda )\). At the end, the reduction knows the answer to all leakage queries of \({\textsf {A}}^*\) with hard-wired randomness r, which allows to play the game with the challenger as explained above.
4.3 Hybrids
Let us start by recalling the definition of experiment \(\mathbf{Tamper} _{\Gamma ^*, {\textsf {A}}^*}(\lambda , b)\) for our code from Fig. 1.

Consider the following hybrid experiments.
-
\(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^1(\lambda , b)\): Let \(\textsf {S}= (\textsf {S}_0, \textsf {S}_1)\) be the zero-knowledge simulator guaranteed by the non-interactive argument system. This hybrid is identical to the original experiment, except that the instructions
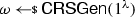 and
and 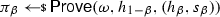 are replaced by
are replaced by 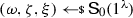 and
and 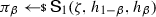 respectively.
respectively. -
\(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^2(\lambda , b)\): Identical to the previous experiment, except that the oracle \({\mathcal {O}}_\mathsf{maul}\) is replaced by \({\mathcal {O}}_\mathsf{maul}'\) described in Fig. 2.
We first prove, in Sect. 4.4, that

Then, in Sect. 4.5, we show that the above hybrids are computationally close, i.e., for all \(b\in \{0,1\}\):

thus proving continuous non-malleability:

4.4 The Main Reduction
Lemma 2

Proof
The proof is down to the augmented leakage resilience (cf. Definition 5) of the underlying LRS \((\textsf {LREnc},\textsf {LRDec})\). The reduction relies on a family of weakly universalFootnote 13 hash functions \(\Psi \). By contradiction, assume that there exists a PPT adversary \({\textsf {A}}^* = ({\textsf {A}}^*_0,{\textsf {A}}^*_1)\) that can tell apart \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^2(\lambda , 0)\) and \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^2(\lambda , 1)\) with non-negligible probability. Consider the following PPT attacker \({\textsf {A}}\) against leakage resilience of \((\textsf {LREnc},\textsf {LRDec})\), which relies on the leakage functions defined in Fig. 3 on the following page.
\(\underline{\hbox {Attacker }{\textsf {A}}\hbox { for }(\textsf {LREnc},\textsf {LRDec}):}\)
- 1.
(Setup phase.) Simulate the CRS as follows:
- (a)
Run
and
; set \(\omega ^* = (\omega , \textit{hk})\).
- (b)
Sample
, and run
.
- (c)
Forward \((m_0, m_1)\) to the challenger, obtaining access to the leakage oracles \({\mathcal {O}}_\textsf {leak}^\ell (s_0,\cdot )\) and \({\mathcal {O}}_\textsf {leak}^\ell (s_1,\cdot )\).
- (d)
For each \(\beta \in \{0,1\}\), query \(g_\beta ^\mathsf{hash}(\textit{hk}, \cdot )\) to \({\mathcal {O}}_\textsf {leak}^\ell (s_\beta ,\cdot )\), obtaining \(h_\beta = \textsf {Hash}(\textit{hk},s_\beta )\).
- (e)
For each \(\beta \in \{0,1\}\) generate the argument
.
- (f)
Let \({{\hat{\alpha }}} := (\omega ,\textit{hk},\xi ,h_0,h_1,\pi _0,\pi _1,\langle {\textsf {A}}_1^*\rangle ,\alpha _1,r_1)\), and \(\Lambda _0,\Lambda _1 := (\varepsilon , \ldots , \varepsilon )\) be initially empty arrays.
- 2.
(Obtain the temporary leakages.) Run the following loop:
- (a)
Query alternatively \({\mathcal {O}}_\textsf {leak}^\ell (s_0,\cdot )\) and \({\mathcal {O}}_\textsf {leak}^\ell (s_1,\cdot )\) with \(g_0^\mathsf{temp}({{\hat{\alpha }}}, \Lambda _0,\Lambda _1,\cdot )\) and \(g_1^\mathsf{temp}({{\hat{\alpha }}}, \Lambda _0,\Lambda _1,\cdot )\).
- (b)
For any \(j\ge 1\), after the j-th query, if at least one of the oracles returns \((0,\Lambda _\beta ^{(j)})\) update the j-th entry of \(\Lambda _\beta \) as in \(\Lambda _\beta [j] = \Lambda _\beta ^{(j)}\).
- (c)
If both oracles return \((1,q_0)\) and \((1,q_1)\), respectively, break the loop obtaining the (temporary) leakages \(\Lambda _0,\Lambda _1\) and the (temporary) number of tampering queries \(q = \min \{q_0,q_1\}\).
- 3.
(Learn the self-destruct index.) Set \((q_\mathsf{min}, q_\mathsf{max}) = (0, q)\). Run the following loop:
- (a)
If \(q_\mathsf{min} = q_\mathsf{max}\), break the loop obtaining the self-destruct index \(i^* := q_\mathsf{min} = q_\mathsf{max}\); else, set \(q_\mathsf{med} = \lfloor \frac{q_\mathsf{min} + q_\mathsf{max}}{2}\rfloor \).
- (b)
Sample
.
- (c)
For each \(\beta \in \{0,1\}\), query \(g_\beta ^\mathsf{sd}({{\hat{\alpha }}}, \Lambda _0, \Lambda _1, \psi _t,q_\mathsf{med}, \cdot )\) to \({\mathcal {O}}_\textsf {leak}^\ell (s_\beta ,\cdot )\) obtaining a value \(y_\beta \in \{0,1\}^\lambda \).
- (d)
If \(y_0 \ne y_1\), update \((q_\mathsf{min}, q_\mathsf{max}) \leftarrow (q_\mathsf{min}, q_\mathsf{med})\); else, update \((q_\mathsf{min}, q_\mathsf{max}) \leftarrow (q_\mathsf{med} + 1, q_\mathsf{max})\).
- 4.
(Correct the leakages.) Set \(\Lambda _0,\Lambda _1 \leftarrow (\varepsilon ,\ldots ,\varepsilon )\), i.e., discard all the temporary leakages. Run the following loop:
- (a)
Query alternatively \({\mathcal {O}}_\textsf {leak}^\ell (s_0,\cdot )\) and \({\mathcal {O}}_\textsf {leak}^\ell (s_1,\cdot )\) with \(g_0^\mathsf{leak}({{\hat{\alpha }}}, \Lambda _0,\Lambda _1, i^*,\cdot )\) and \(g_1^\mathsf{leak}({{\hat{\alpha }}}, \Lambda _0,\Lambda _1, i^*,\cdot )\).
- (b)
For any \(j\ge 1\), after the j-th query, if at least one of the oracles returns \((0,\Lambda _\beta ^{(j)})\) update the j-th entry of \(\Lambda _\beta \) as in \(\Lambda _\beta [j] = \Lambda _\beta ^{(j)}\).
- (c)
If both oracles return 1, break the loop obtaining the final leakages \(\Lambda _0,\Lambda _1\).
- 5.
(Play the game.) Run the following loop:
- (a)
Forward \(\sigma = 0\) to the challenger, obtaining \(s_0\).
- (b)
Set \(c_0 = (s_0,h_1,\pi _0,\pi _1)\), then start \({\textsf {A}}_1^*(1^\lambda ,\alpha _1;r_1)\).
- (c)
Upon input the j-th leakage query \((g_0^{(j)},g_1^{(j)})\) from \({\textsf {A}}_1^*\), return \((\Lambda _0^{(j)},\Lambda _1^{(j)})\).
- (d)
Upon input the i-th tampering query \((f_0^{(i)},f_1^{(i)})\) from \({\textsf {A}}_1^*\):
If \(i < i^*\), answer with \(\Theta _0^{(i)} = \textsf {SimTamp}(c_0,f_0^{(i)})\).
If \(i \ge i^*\), return \(\bot \).
- (e)
Upon input a guess \(b'\) from \({\textsf {A}}_1^*\), forward \(b'\) to the challenger and terminate.
For the analysis, we must show that \({\textsf {A}}\) does not leak too much information and that the reduction is correct (in the sense that the view of \({\textsf {A}}^*\) is simulated correctly). Note that \({\textsf {A}}\) makes leakage queries in steps 1d, 2a, 3c, and 4a. The leakage amount in step 1d is equal to \(\lambda \) bits per share (i.e., the size of a hash value). The leakage amount in step 2a is bounded by \(\ell ^* + O(\log \lambda )\) bits per share (i.e., the maximum leakage asked by \({\textsf {A}}^*\) plus the indexes \(q_0,q_1\)); by a similar argument, the leakage in step 4a consists of at most \(\ell ^*\) bits per share. Finally, the leakage in step 3c is bounded by \(O(\lambda \log (\lambda ))\) (as the loop for the binary search is run at most \(O(\log \lambda )\) times, and each time the reduction leaks \(\lambda \) bits per share). Putting it all together, the overall leakage is bounded by
where the inequality follows by the bound on \(\ell ^*\) in the theorem statement.
Next, we argue that \({\textsf {A}}\) perfectly simulates the view of \({\textsf {A}}^*\) except with negligible probability. Indeed:
-
The distribution of the CRS \(\omega ^* = (\omega ,\textit{hk})\) is perfect.
-
For each \(\beta \in \{0,1\}\), the distribution of the value \(c_\beta \) assembled inside the leakage oracle \({\mathcal {O}}_\textsf {leak}^\ell (s_\beta ,\cdot )\) is identical to that of the target codeword \(c^* = (c_0,c_1)\) in \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^2(\lambda ,b)\), where b is the hidden bit in the security game for \((\textsf {LREnc},\textsf {LRDec})\).
-
The simulation of \({\textsf {A}}^*\)’s leakage queries is perfect. Note that the simulated leakages \(\Lambda _0,\Lambda _1\) might be inconsistent after the loop of step 2 terminates. This is because there may exist an index \(i\in [q]\) such that \(\Theta _0^{(i)} \ne \Theta _1^{(i)}\) (i.e., the answer to the i-th tampering query should be \(\bot \), but a different value is passed to \({\textsf {A}}_1^*\) inside the leakage oracle), which causes a wrong simulation of all leakage queries \(j \ge i\) (if any). However, the reduction adjusts the leakages later in step 4, after the index \(i^*\) corresponding to the self-destruct query is known.
-
Except with negligible probability, the index \(i^*\) coincides with the index corresponding to the self-destruct query, i.e. the minimum \(i^*\in [q]\) such that \(\Theta _0^{(i^*)} \ne \Theta _1^{(i^*)}\) in \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^2(\lambda ,b)\). The latter follows readily from the weak universality of \(\Psi \), as for each query \(g_0^\mathsf{sd}({{\hat{\alpha }}},\Lambda _0,\Lambda _1,\psi _t,q_\mathsf{med},\cdot )\) and \(g_1^\mathsf{sd}({{\hat{\alpha }}},\Lambda _0,\Lambda _1,\psi _t,q_\mathsf{med},\cdot )\) the probability that
$$\begin{aligned} y_0 = \psi _t(\Theta _0^{(1)}||\cdots ||\Theta _0^{(q_\mathsf{med})}) = \psi _t(\Theta _1^{(1)}||\cdots ||\Theta _1^{(q_\mathsf{med})})=y_1, \end{aligned}$$but \(\Theta _0^{(1)}||\cdots ||\Theta _0^{(q_\mathsf{med})} \ne \Theta _1^{(1)}||\cdots ||\Theta _1^{(q_\mathsf{med})}\) is at most \(2^{-\lambda }\) (over the choice of
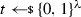 ), and thus, by the union bound, the simulation is wrong with probability at most \(q\cdot 2^{-\lambda }\).
), and thus, by the union bound, the simulation is wrong with probability at most \(q\cdot 2^{-\lambda }\). -
In step 5, the reduction obtains \(c_0\), and thus can use the knowledge of the final corrected leakages \(\Lambda _0,\Lambda _1\) and of the self-destruct index \(i^*\) to perfectly simulate all the queries of \({\textsf {A}}_1^*\).
Hence, we have shown that there exists a polynomial \(p(\lambda )\in \texttt {poly}(\lambda )\) and a negligible function \(\nu :{\mathbb {N}}\rightarrow [0,1]\) such that
This concludes the proof. \(\square \)
4.5 Indistinguishability of the Hybrids
We first establish some useful lemmas, and then analyze each of the two game hops individually.
4.5.1 Useful Lemmata
Lemma 3
The code \(\Gamma ^* = (\textsf {Init}^*,\textsf {Enc}^*,\textsf {Dec}^*)\) satisfies codewords uniqueness. Moreover, the latter still holds if we modify \((\textsf {Init}^*,\textsf {Enc}^*)\) as defined in \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^1(\lambda , b)\).
Proof
We show that Definition 7 is satisfied for \(\beta = 0\). The proof for \(\beta = 1\) is analogous, and therefore omitted.
Assume that there exists a PPT adversary \({\textsf {A}}^*\) that, given as input \(\omega ^* = (\omega ,\textit{hk})\), is able to produce \((c_0,c_1,c_1')\) such that both \((c_0,c_1)\) and \((c_0,c_1')\) are valid, but \(c_1 \ne c_1'\). Let \(c_0 = (s_0,h_1,\pi _0,\pi _1)\), \(c_1 = (s_1,h_0,\pi _0,\pi _1)\), and \(c_1' = (s_1',h_0',\pi _0',\pi _1')\). Since \(s_0\) is the same in both codewords, we must have \(h_0 = h_0'\) as the hash function is deterministic. Furthermore, since both \((c_0,c_1)\) and \((c_0,c_1')\) are valid, the arguments on the right parts must be equal to the ones on the left part, i.e., \(\pi _0' = \pi _0\) and \(\pi _1' = \pi _1\). It follows that \(c_1' = (s_1',h_0,\pi _0,\pi _1)\), with \(s_1' \ne s_1\), and thus \((s_1,s_1')\) are a collision for \(\textsf {Hash}(\textit{hk},\cdot )\). The latter contradicts collision resistance of \((\textsf {Gen},\textsf {Hash})\), as it can be seen by the simple reduction that given a target hash key \(\textit{hk}\) embeds it in the CRS \(\omega ^* = (\omega ,\textit{hk})\), runs \({\textsf {A}}^*(1^\lambda ,\omega ^*)\) obtaining \((c_0,c_1,c_1')\), and outputs \((s_1,s_1')\).
The second part of the statement of the lemma follows by the non-interactive zero-knowledge property of the argument system. In fact, the latter implies that the advantage of any PPT adversary \({\textsf {A}}^*\) in breaking codewords uniqueness must be close (up to a negligible distance) in the first hybrid and in the original experiment. \(\square \)
Lemma 4
Whenever \({\textsf {A}}^*\) outputs a Type-D query in \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^1(\lambda , b)\) the following holds: For all \(\beta \in \{0,1\}\) the codeword \((\tilde{c}_{0,\beta },\tilde{c}_{1,\beta })\) contained in \(\Theta _\beta \) must be valid with overwhelming probability.
Proof
Fix any \(\beta \in \{0,1\}\), and let \((f_0,f_1)\) be a generic query of Type D. Denote by \(\Theta _\beta = (\tilde{c}_{0,\beta },\tilde{c}_{1,\beta })\) the answer to any tampering query \((f_0,f_1)\) as it would be computed by \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),(f_0,f_1))\), i.e., \(\tilde{c}_{\beta ,\beta } = (\tilde{s}_\beta ,\tilde{h}_{1-\beta },\tilde{\pi }_{0,\beta },\tilde{\pi }_{1,\beta })\) and \(\tilde{c}_{1-\beta ,\beta } = (\tilde{s}_{1-\beta },\tilde{h}_{\beta ,\beta },\tilde{\pi }_{0,\beta },\tilde{\pi }_{1,\beta })\) with \(\tilde{h}_{\beta ,\beta } = \textsf {Hash}(\textit{hk},\tilde{s}_\beta )\). By construction, \((\tilde{c}_{0,\beta },\tilde{c}_{1,\beta })\) is invalid if and only if \(\textsf {Hash}(\textit{hk},\tilde{s}_{1-\beta }) \ne \tilde{h}_{1-\beta }\).
Fix \(b\in \{0,1\}\). Let now \({\textsf {A}}^*\) be a PPT adversary for \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^1(\lambda , b)\) that with probability at least \(1/\texttt {poly}(\lambda )\) outputs a Type-D tampering query \((f_0,f_1)\) such that \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),(f_0,f_1))\) would yield an invalid codeword \(\Theta _\beta \) as described above. We construct a PPT attacker \({\textsf {A}}\) against true-simulation extractability (cf. Definition 3) of the non-interactive argument system. A description of \({\textsf {A}}\) follows:
\(\underline{\hbox {Attacker }{\textsf {A}}\hbox { for }(\textsf {CRSGen}, \textsf {Prove}, \textsf {Ver}):}\)
Upon receiving the target CRS \(\omega \), generate
and let \(\omega ^* := (\omega , \textit{hk})\).
Run
, and let
.
Compute \(h_0 = \textsf {Hash}(\textit{hk},s_0)\) and \(h_1 = \textsf {Hash}(\textit{hk},s_1)\); forward \((h_{1},(s_0,h_0))\) and \((h_0,(s_1,h_1))\) to the challenger, obtaining arguments \(\pi _0\) and \(\pi _1\).
Let \(c^* = (c_0,c_1) = ((s_0,h_1,\pi _0,\pi _1),(s_1,h_0,\pi _0,\pi _1))\), and pick
where \(q\in \texttt {poly}(\lambda )\) is an upper bound for the number of \({\textsf {A}}^*\)’s tampering queries.
Run \({{\textsf {A}}_1^*}^{{\mathcal {O}}_\textsf {leak}^{\ell ^*}(c_0,\cdot ),{\mathcal {O}}_\textsf {leak}^{\ell ^*}(c_1,\cdot ),{\mathcal {O}}_\mathsf{maul}((c_0,c_1),\cdot )}(1^\lambda ,\alpha _1)\) by answering all of its leakage and tampering queries as follows:
Upon input a leakage query \(g_0\) (resp. \(g_1\)) for \({\mathcal {O}}_\textsf {leak}^{\ell ^*}(c_0,\cdot )\) (resp. \({\mathcal {O}}_\textsf {leak}^{\ell ^*}(c_1,\cdot )\)), return \(g_0(c_0)\) (resp. \(g_1(c_1)\)).
Upon input a tampering query \((f_0,f_1)\) for \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(\cdot ,\cdot ))\), if this is not the \(j^*\)-th tampering query answer in the same way as \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(\cdot ,\cdot ))\) would do. Else, run \(\tilde{c}_\beta = (\tilde{s}_\beta ,\tilde{h}_{1-\beta },\tilde{\pi }_{0,\beta },\tilde{\pi }_{1,\beta }) = f_\beta (c_\beta )\), compute \(\tilde{h}_{\beta ,\beta } = \textsf {Hash}(\textit{hk},s_\beta )\) and forward \((\tilde{h}_{1-\beta },\tilde{h}_{\beta ,\beta },\tilde{\pi }_{1,\beta })\) to the challenger.
For the analysis, note that the simulation done by \({\textsf {A}}\) is perfect. In particular, both the distribution of the CRS and the answer to \({\textsf {A}}^*\)’s leakage and tampering queries is identical to that of \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^1(\lambda ,b)\). It follows that, with probability at least \(1/q \cdot 1/\texttt {poly}(\lambda ) \in 1/\texttt {poly}(\lambda )\), the \(j^*\)-th tampering query output by attacker \({\textsf {A}}^*\) is such that all of the following conditions are met: (i) \(\textsf {Ver}(\omega ,\tilde{h}_{\beta ,\beta },(\tilde{h}_{1-\beta },\tilde{\pi }_{1,\beta })) = 1\); (ii) \((\tilde{h}_{1-\beta },\tilde{h}_{\beta ,\beta },\tilde{\pi }_{1-\beta ,\beta })\) is fresh, i.e., it is different from \((h_{1-\beta },h_\beta ,\pi _{1-\beta })\); (iii) \(\textsf {K}(\xi ,\tilde{h}_{\beta ,\beta },(\tilde{h}_{1-\beta },\tilde{\pi }_{1,\beta }))\) outputs a value \(\tilde{s}_{1-\beta }\) such that \(\textsf {Hash}(\textit{hk},\tilde{s}_{1-\beta }) \ne \tilde{h}_{1-\beta }\) (i.e., \((\tilde{h}_{1-\beta },\tilde{s}_{1-\beta }) \not \in \mathcal {R}_\mathsf{hash}^\textit{hk}\)). Further, note that \({\textsf {A}}\) obtains only simulated arguments for true statements. Thus, \({\textsf {A}}\) breaks true-simulation extractability with non-negligible probability. The lemma follows: \(\square \)
4.5.2 First Game Hop
Lemma 5
\(\forall b\in \{0,1\}\): 
Proof
The proof is down to the adaptive multi-theorem zero-knowledge property (cf. Definition 2) of the underlying non-interactive argument system. By contradiction, assume that there exists a PPT attacker \({\textsf {A}}^* = ({\textsf {A}}_0^*, {\textsf {A}}_1^*)\) that, for any fixed \(b\in \{0,1\}\), can distinguish between  and
and  with non-negligible probability. Consider the following PPT distinguisher \({\textsf {D}}\) attacking the zero-knowledge property.
with non-negligible probability. Consider the following PPT distinguisher \({\textsf {D}}\) attacking the zero-knowledge property.
\(\underline{\hbox {Distinguisher }{\textsf {D}}\hbox { for }(\textsf {CRSGen}, \textsf {Prove}, \textsf {Ver}):}\)
Upon receiving the target CRS \(\omega \), generate
and let \(\omega ^* := (\omega , \textit{hk})\).
Run
, and let
.
For each \(\beta \in \{0,1\}\), compute \(h_\beta = \textsf {Hash}(\textit{hk},s_\beta )\).
For each \(\beta \in \{0,1\}\), forward \((h_{1-\beta },(h_\beta ,s_\beta ))\) to the challenger, obtaining \(\pi _0,\pi _1\).
Let \(c^* = (c_0,c_1) = ((s_0,h_1,\pi _0,\pi _1),(s_1,h_0,\pi _0,\pi _1))\).
Run
.
Output \(b'\).
For the analysis, note that the simulation done by \({\textsf {D}}\) is perfect. In particular, depending on the game that \({\textsf {D}}\) is playing, the CRS \(\omega \) is either generated by running \(\textsf {CRSGen}(1^\lambda )\) or \(\textsf {S}_0(1^\lambda )\); similarly, the arguments \(\pi _0,\pi _1\) are either obtained by running  or
or  . Moreover, the reduction can perfectly emulate the oracles \({\mathcal {O}}_\mathsf{maul}\) and \({\mathcal {O}}_\textsf {leak}^{\ell ^*}\) since it holds a simulated codeword \(c^*\) that is either distributed according to \(\mathbf{Tamper} _{\Gamma ^*, {\textsf {A}}^*}(\lambda , b)\) or \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^1(\lambda , b)\). Thus, \({\textsf {D}}\) has the same distinguishing advantage as that of \({\textsf {A}}^*\). The lemma follows: \(\square \)
. Moreover, the reduction can perfectly emulate the oracles \({\mathcal {O}}_\mathsf{maul}\) and \({\mathcal {O}}_\textsf {leak}^{\ell ^*}\) since it holds a simulated codeword \(c^*\) that is either distributed according to \(\mathbf{Tamper} _{\Gamma ^*, {\textsf {A}}^*}(\lambda , b)\) or \(\mathbf{Hyb} _{\Gamma ^*, {\textsf {A}}^*}^1(\lambda , b)\). Thus, \({\textsf {D}}\) has the same distinguishing advantage as that of \({\textsf {A}}^*\). The lemma follows: \(\square \)
4.5.3 Second Game Hop
Lemma 6
\(\forall b\in \{0,1\}\): 
Proof
Fix \(b\in \{0,1\}\). We will prove that, with all but a negligible probability, the output of the tampering oracles \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),\cdot )\) and \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),\cdot )\) are identical up to the first tampering query that is answered with \(\bot \) in \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),\cdot )\). (Afterward, both oracles self-destruct and thus always return \(\bot \).) Let \(q\in \texttt {poly}(\lambda )\) be an upper bound on the number of tampering queries in either of the hybrids. Consider the following events, defined over the probability space of both \(\mathbf{Hyb} _{\Sigma ^*, {\textsf {A}}}^1(\lambda , b)\) and \(\mathbf{Hyb} _{\Sigma ^*, {\textsf {A}}}^2(\lambda , b)\):
-
Event \(\mathbf{Bad} _\mathsf{same}\): There exists an index \(i\in [q]\), corresponding to a tampering query \((f_0^{(i)},f_1^{(i)})\), such that oracle \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) outputs \(\diamond \), whereas oracle \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) would output a value in \(\{0,1\}^{2n} \cup \{\bot \}\).
-
Event \(\mathbf{Bad} _{\bot }\): There exists an index \(i\in [q]\), corresponding to a tampering query \((f_0^{(i)},f_1^{(i)})\), such that oracle \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) outputs \(\bot \), whereas oracle \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) would output a value in \(\{0,1\}^{2n} \cup \{\diamond \}\).
-
Event \(\mathbf{Bad} _\mathsf{cdw}\): There exists an index \(i\in [q]\), corresponding to a tampering query \((f_0^{(i)},f_1^{(i)})\), such that oracle \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) outputs a codeword \((\tilde{c}_0^{(i)},\tilde{c}_1^{(i)})\), whereas oracle \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) would output either a different codeword or a value in \(\{\diamond ,\bot \}\).
Denote by \(\mathbf{Bad} := \mathbf{Bad} _\mathsf{same} \cup \mathbf{Bad} _{\bot } \cup \mathbf{Bad} _\mathsf{cdw}\). Since the two hybrids are identical conditioned on \(\mathbf{Bad} \) not happening, by a standard argument, it suffices to prove that \(\mathbf{Bad} \) happens with at most a negligible probability. In what follows, we always write
for the tampered codeword \((\tilde{c}_0^{(i)},\tilde{c}_1^{(i)})\) associated with \((f_0^{(i)},f_1^{(i)})\), and \(\tilde{h}_{\beta ,\beta }\) for the value \(\textsf {Hash}(\textit{hk},\tilde{s}_\beta )\).
Claim 1
\({\mathbb {P}}\left[ \mathbf{Bad} _\mathsf{same}\right] = 0\).
Proof
Note that \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) outputs \(\diamond \) if and only if \((f_0^{(i)},f_1^{(i)})\) is of Type A, i.e., \(\tilde{c}_0^{(i)} = f_0^{(i)}(c_0) = c_0\) and \(\tilde{c}_1^{(i)} = f_1^{(i)}(c_1) = c_1\). However, for such a query, oracle \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) would also return \(\diamond \), and thus the event \(\mathbf{Bad} _\mathsf{same}\) never happens. \(\square \)
Claim 2
\({\mathbb {P}}\left[ \mathbf{Bad} _{\bot }\right] \in \texttt {negl}(\lambda )\).
Proof
Note that \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) outputs \(\bot \) if and only if either (i) \(\exists \beta \in \{0,1\}:\Theta _\beta [i] = \bot \), or if (ii) \(\bot \ne \Theta _0[i] \ne \Theta _1[i] \ne \bot \). We treat each of these sub-cases separately.
The case \(\exists \beta \in \{0,1\}:\Theta _\beta [i] = \bot \). We observe that \(\Theta _\beta [i] = \bot \) if and only if one of the following events happen: (a) \(f_\beta ^{(i)}\) is of Type B; (b) \(f_\beta ^{(i)}\) is of Type C; (c) \(f_\beta ^{(i)}\) is of Type D, and the extractor \(\textsf {K}\) returns \(\bot \). Below, we analyze each such case.
- Type-B queries::
-
Recall that function \(f_\beta ^{(i)}\) is of Type B if:
$$\begin{aligned} \textsf {Ver}(\omega ,\tilde{h}_{1-\beta }^{(i)},(\tilde{h}_{\beta ,\beta }^{(i)},\tilde{\pi }_{\beta ,\beta }^{(i)})) = 0 \vee \textsf {Ver}(\omega ,\tilde{h}_{\beta ,\beta }^{(i)},(\tilde{h}_{1-\beta }^{(i)},\tilde{\pi }_{1-\beta ,\beta }^{(i)})) = 0. \end{aligned}$$The above means that the local check on \(\tilde{c}_\beta ^{(i)}\) (as run by the original decoding algorithm) fails, and thus \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) would also return \(\bot \).
- Type-C queries::
-
Wlog. assume that \(f_0^{(i)}\) is of Type C (the proof in case \(f_1^{(i)}\) is of Type C being analogous). Recall that function \(f_0^{(i)}\) is of Type C if:
$$\begin{aligned} (\tilde{h}_{1}^{(i)},\tilde{h}_{0,0}^{(i)},\tilde{\pi }_{1,0}^{(i)}) = (h_{1},h_{0},\pi _{1}). \end{aligned}$$
Assume now that \((f_{0}^{(i)},f_1^{(i)})\) is such that \({\mathcal {O}}_\mathsf{maul}\) returns a value different from \(\bot \). We claim this implies that the tampered codeword \((\tilde{c}_0^{(i)},\tilde{c}_1^{(i)})\) must be of the form \(((s_0,h_1,\tilde{\pi }_0^{(i)},\pi _1),(s_1,h_0,\tilde{\pi }_0^{(i)},\pi _1))\). First, collision resistanceFootnote 14 of \((\textsf {Gen},\textsf {Hash})\) implies that \(\tilde{s}_0^{(i)} = s_0\) and \(\tilde{s}_1^{(i)} = s_1\) with all but a negligible probability. Second, \(\tilde{\pi }_{1,1}^{(i)} = \pi _1\) and \(\tilde{\pi }_{0,0}^{(i)} = \tilde{\pi }_{0,1}^{(i)} = \tilde{\pi }_{0}^{(i)}\) as otherwise the tampered codeword would not be valid.
Next, we prove that the above contradicts security of the LRS. By contradiction, assume that there exists an adversary \({\textsf {A}}^*\) that with non-negligible probability outputs a tampering query \((f_0^{(i)},f_1^{(i)})\) such that \((\tilde{c}_0^{(i)},\tilde{c}_1^{(i)}) = ((s_0,h_1,\tilde{\pi }_0^{(i)},\pi _1),(s_1,h_0,\tilde{\pi }_0^{(i)},\pi _1))\), with \(\tilde{\pi }_0^{(i)} \ne \pi _0\) (otherwise \(f_0^{(i)}\) would be of Type A). Since \(\tilde{\pi }_0^{(i)}\) is accepting, by true-simulation extractability of the argument system \((\textsf {CRSGen},\textsf {Prove},\textsf {Ver})\), it holds that \(\textsf {K}(\xi ,h_{1},(h_{0},\tilde{\pi }_{0}^{(i)}))\) outputs a value \(\tilde{s}_0^{(i)}\) such that \(\textsf {Hash}(\textit{hk},\tilde{s}_0^{(i)}) = h_0\) with all but a negligible probability.Footnote 15 Moreover, collision resistance of \((\textsf {Gen},\textsf {Hash})\) implies that in this case \(\tilde{s}_0^{(i)} = s_0\) with overwhelming probability.Footnote 16 Consider now the following attacker \({\textsf {A}}\).
\(\underline{\hbox {Attacker }{\textsf {A}}\hbox { against }(\textsf {LREnc},\textsf {LRDec}):}\)
Run steps 1–4 as described in the reduction \({\textsf {A}}\) in the proof of Lemma 2. This yields target messages \(m_0,m_1\) (as returned by \({\textsf {A}}_0^*\)), the final corrected leakages \(\Lambda _0,\Lambda _1\), the index \(i^*\) corresponding to the self-destruct query, and auxiliary information \({{\hat{\alpha }}} = (\omega ,\textit{hk},\xi ,h_0,h_1,\pi _0,\pi _1,\langle {\textsf {A}}_1^*\rangle ,\alpha _1,r_1)\).
Forward \(\sigma = 1\) to the challenger, obtaining \(s_1\).
Set \(c_1 = (s_1,h_0,\pi _0,\pi _1)\), sample
, and then start \({\textsf {A}}_1^*(1^\lambda ,\alpha _1;r_1)\).
Upon input the j-th leakage query \((g_0^{(j)},g_1^{(j)})\) from \({\textsf {A}}_1^*\), return \((\Lambda _0^{(j)},\Lambda _1^{(j)})\).
Upon input the i-th tampering query \((f_0^{(i)},f_1^{(i)})\) from \({\textsf {A}}_1^*\):
If \(i \ne j^* < i^*\), answer with \(\Theta _1^{(i)} = \textsf {SimTamp}(c_1,f_1^{(i)})\).
If \(i = j^*\), let \(\tilde{c}_1^{(i)} = (\tilde{s}_1^{(i)},\tilde{h}_0^{(i)},\tilde{\pi }^{(i)}_{0,1},\tilde{\pi }^{(i)}_{1,1}):=f_1^{(i)}(s_1,h_0,\pi _0,\pi _1)\). Run \(\tilde{s}_0^{(i)} := \textsf {K}(\xi ,h_{1},(h_{0},\tilde{\pi }_{0,1}^{(i)}))\). If there exists \(b'\in \{0,1\}\) such that \(\textsf {LRDec}(\tilde{s}_0^{(i)},\tilde{s}_1^{(i)}) = m_{b'}\), forward \(b'\) to the challenger and terminate; else, abort the simulation and terminate.
An argument identical to that used in the proof of Lemma 2 shows that \({\textsf {A}}\) leaks at most \(\ell \) bits and perfectly simulates the view of \({\textsf {A}}^*\). Since with probability \(1/\texttt {poly}(\lambda )\) attacker \({\textsf {A}}^*\) outputs a tampering query \((f_0^{(i)},f_1^{(i)})\) such that \((\tilde{c}_0^{(i)},\tilde{c}_1^{(i)}) = ((s_0,h_1,\tilde{\pi }_0^{(i)},\pi _1),(s_1,h_0,\tilde{\pi }_0^{(i)},\pi _1))\), with \(\tilde{\pi }_0^{(i)} \ne \pi _0\), and moreover with probability \(1/i^*\) this is the \(j^*\)-th tampering query, it follows that \(b' = b\) in experiment \(\mathbf{Leak} ^{+}_{\Sigma ,{\textsf {A}}}(\lambda ,b)\) with probability at least \(1/\texttt {poly}(\lambda )-\texttt {negl}(\lambda )\).
- Type-D queries::
-
Wlog. assume that \(f_0^{(i)}\) is of Type D (the proof in case \(f_1^{(i)}\) is of Type D being analogous). Recall that function \(f_0^{(i)}\) is of Type D if:
$$\begin{aligned} (\tilde{h}_{1}^{(i)},\tilde{h}_{0,0}^{(i)},\tilde{\pi }_{1,0}^{(i)}) \ne (h_{1},h_{0},\pi _{1}), \end{aligned}$$and moreover the argument \(\tilde{\pi }_{1,0}^{(i)}\) is valid w.r.t. statement \(\tilde{h}_{1}^{(i)}\) and label \(\tilde{h}_{0,0}^{(i)}\). Lemma 4 implies that in such a situation the extractor \(\textsf {K}\) yields a valid witness, so that \(\Theta _0[i] \ne \bot \) with overwhelming probability.
The case \(\bot \ne \Theta _0[i] \ne \Theta _1[i] \ne \bot \). First note that both \(\Theta _0[i]\) and \(\Theta _1[i]\) must be different from \(\diamond \). This is because if \(\Theta _0[i] = \diamond \), it must be the case that \(\Theta _1[i] \ne \diamond \), and thus \(\tilde{c}_1^{(i)} = f_1^{(i)}(c_1) \ne c_1\) as otherwise \((f_0^{(i)},f_1^{(i)})\) would be of Type A. Since \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) does not output \(\bot \), the above implies that both \((c_0,c_1)\) and \((c_0,\tilde{c}_1^{(i)})\) are valid codewords, which contradicts codewords uniqueness. More formally, given an efficient attacker \({\textsf {A}}^*\) that provokes the above event, it is straightforwardFootnote 17 to construct an efficient attacker \({\textsf {A}}\) that breaks uniqueness, which in turn contradicts Lemma 3.
It remains to analyze the case where both \(\Theta _0[i]\) and \(\Theta _1[i]\) contain values in \(\{0,1\}^{2n}\), i.e., \(\Theta _0[i] = (\tilde{c}_{0,0}^{(i)},\tilde{c}_{1,0}^{(i)})\) and \(\Theta _1[i] = (\tilde{c}_{0,1}^{(i)},\tilde{c}_{1,1}^{(i)})\) with \((\tilde{c}_{0,0}^{(i)},\tilde{c}_{1,0}^{(i)}) \ne (\tilde{c}_{0,1}^{(i)},\tilde{c}_{1,1}^{(i)})\). By definition of \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\), for all \(\beta \in \{0,1\}\), we can write:
However, since \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) does not return \(\bot \), it must hold that \(\tilde{\pi }_{0,0}^{(i)} = \tilde{\pi }_{0,1}^{(i)} := \tilde{\pi }_{0}^{(i)}\) and \(\tilde{\pi }_{1,0}^{(i)} = \tilde{\pi }_{1,1}^{(i)} := \tilde{\pi }_{1}^{(i)}\), and furthermore \(\tilde{h}_{0,0}^{(i)} = \tilde{h}_0^{(i)} := \textsf {Hash}(\textit{hk},\tilde{s}_0^{(i)})\) and \(\tilde{h}_{1,1}^{(i)} = \tilde{h}_1^{(i)} := \textsf {Hash}(\textit{hk},\tilde{s}_1^{(i)})\). But this implies \(\tilde{c}_{0,0} = (\tilde{s}_{0}^{(i)},\tilde{h}_{1}^{(i)},\tilde{\pi }_{0}^{(i)},\tilde{\pi }_{1}^{(i)}) = \tilde{c}_{0,1}\), and similarly \(\tilde{c}_{1,0} = (\tilde{s}_{1}^{(i)},\tilde{h}_{0}^{(i)},\tilde{\pi }_{0}^{(i)},\tilde{\pi }_{1}^{(i)}) = \tilde{c}_{1,1}\), a contradiction. \(\square \)
Claim 3
\({\mathbb {P}}\left[ \mathbf{Bad} _\mathsf{cdw}\right] \in \texttt {negl}(\lambda )\).
Proof
Note that \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) outputs \((\tilde{c}_0^{(i)},\tilde{c}_1^{(i)})\) if and only if \(\Theta _0[i] = (\tilde{c}_{0,0}^{(i)},\tilde{c}_{1,0}^{(i)})\), \(\Theta _1[i] = (\tilde{c}_{0,1}^{(i)},\tilde{c}_{1,1}^{(i)})\), and moreover \((\tilde{c}_{0,0}^{(i)},\tilde{c}_{1,0}^{(i)}) = (\tilde{c}_{0,1}^{(i)},\tilde{c}_{1,1}^{(i)}) := (\tilde{c}_0^{(i)},\tilde{c}_1^{(i)})\). Let us write \(\tilde{c}_0^{(i)} = (\tilde{s}_{0}^{(i)},\tilde{h}_{1}^{(i)},\tilde{\pi }_{0}^{(i)},\tilde{\pi }_{1}^{(i)})\) and \(\tilde{c}_1^{(i)} = (\tilde{s}_{1}^{(i)},\tilde{h}_{0}^{(i)},\tilde{\pi }_{0}^{(i)},\tilde{\pi }_{1}^{(i)})\). By Lemma 4, we know that \((\tilde{c}_0^{(i)},\tilde{c}_1^{(i)})\) is a valid codeword with overwhelming probability.
First, we claim that \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) cannot output \(\diamond \). This is because the latter would imply that \(\tilde{c}_0^{(i)} = c_0\) and \(\tilde{c}_1^{(i)} = c_1\), which means \((f_0^{(i)},f_1^{(i)})\) would be of Type A.
Second, let us argue that \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) cannot output \(\bot \) either. This is because the latter would imply that either (i) \(\exists \beta \in \{0,1\}:\textsf {Hash}(\textit{hk},\tilde{s}_\beta ^{(i)}) \ne \tilde{h}_\beta ^{(i)}\), or (ii) \(\exists \beta \in \{0,1\}:\textsf {Ver}(\omega ,\tilde{h}_\beta ^{(i)},(\tilde{h}_{1-\beta }^{(i)},\tilde{\pi }_{1-\beta }^{(i)})) = 0\). However, both these conditions contradict the fact that \((\tilde{c}_0^{(i)},\tilde{c}_1^{(i)})\) must be valid.
It remains to consider the case where \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\) outputs a codeword \(({\hat{c}_{0}}^{(i)},{\hat{c}_{1}}^{(i)}) \ne (\tilde{c}_0^{(i)},\tilde{c}_1^{(i)})\), where \(({\hat{c}_{0}}^{(i)},{\hat{c}_{1}}^{(i)})\) is a valid codeword. Let us generically write \({\hat{c}_{0}}^{(i)} = f_0^{(i)}(c_0) = ({\hat{s}_{0}}^{(i)},{\hat{h}_{1}}^{(i)},{\hat{\pi }}_{0}^{(i)},{\hat{\pi }_{1}}^{(i)})\) and \({\hat{c}_{1}}^{(i)} = f_1^{(i)}(c_1) = ({\hat{s}}_{1}^{(i)},{\hat{h}}_{0}^{(i)},{\hat{\pi }_{0}}^{(i)},{\hat{\pi }_{1}}^{(i)})\) for the tampered codeword as computed by \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\). By definition of \({\mathcal {O}}_\mathsf{maul}'((c_0,c_1),(f_0^{(i)},f_1^{(i)}))\), however, it must be the case that \(\tilde{s}_0^{(i)} = {\hat{s}}_0^{(i)}\) and \(\tilde{s}_1^{(i)} = {\hat{s}_{1}}^{(i)}\), which in turn implies \(\tilde{h}_0^{(i)} = \textsf {Hash}(\textit{hk},\tilde{s}_0^{(i)}) = {\hat{h}_{0}}^{(i)}\) and \(\tilde{h}_{1} = \textsf {Hash}(\textit{hk},\tilde{s}_1) = {\hat{h}_{1}}^{(i)}\), and furthermore \((\tilde{\pi }_0^{(i)},\tilde{\pi }_1^{(i)}) = ({\hat{\pi }_{0}}^{(i)},{\hat{\pi }_{1}}^{(i)})\). Hence, \((\tilde{c}_0^{(i)},\tilde{c}_1^{(i)}) = ({\hat{c}_{0}}^{(i)},{\hat{c}_{1}}^{(i)})\), a contradiction.
\(\square \)
The statement of the lemma now follows by the above claims, together with a union bound. \(\square \)
4.6 Concrete Instantiation
Below, we explain how to instantiate the building blocks required for our code, both from generic and concrete assumptions.
-
Leakage-Resilient Storage As shown in [50, 52], this primitive exists unconditionally. Let \({\mathbb {F}}= \mathbb {GF}(2^k)\) be the Galois field with \(2^k\) elements, and \(t\in {\mathbb {N}}\) be a parameter. Given \(m\in \{0,1\}^k\), algorithm \(\textsf {LREnc}\) interprets \(m\) as an element of \({\mathbb {F}}\) and outputs random \(s_0,s_1\in {\mathbb {F}}^t\) subject to \(\langle s_0,s_1\rangle := \sum _{i=1}^ts_0[i]\cdot s_1[i] = m\). For any \(\delta \in [0,1]\), this yields an \(\ell \)-LRS with \(\ell = kt/4 - \log (1/\delta )\), where \(\delta \) is the statistical distance between the experiments of Definition 4. By Theorem 1, this is also an augmented \((kt/4 - \log (1/\delta )-1)\)-LRS.
-
Collision-Resistant Hash Function Let \({\mathbb {G}}\) be a cyclic group of prime order q, with generators \(g_1,\ldots ,g_t\) for some parameter \(t\in {\mathbb {N}}\). Assuming hardness of the Discrete Logarithm problem, we can take \(\textsf {Hash}(\textit{hk},s) := \prod _{i=1}^t g_i^{s[i]}\) where \(s= (s[1],\ldots ,s[t])\in {\mathbb {Z}}_q^t\) and \(\textsf {Hash}:{\mathbb {Z}}_q^t\rightarrow {\mathbb {G}}\).
-
True-Simulation Extractable NIZK It is well known that simulation extractable NIZKs (i.e., NIZKs that are extractable even in case the attacker observes simulated arguments of possibly false statements) can be obtained for all of NP assuming (doubly enhanced) trapdoor permutations [51, 68, 87]. More concretely, using the collision-resistant hash function from the previous bullet point, we need to consider the NP-relation:
$$\begin{aligned} \mathcal {R}_\mathsf{hash}^{({\mathbb {G}},g_1,\ldots ,g_t,q)} := \left\{ (h,s):~h= \prod _{i=1}^tg_i^{s[i]}\right\} \subseteq {\mathbb {G}} \times {\mathbb {Z}}_q^t. \end{aligned}$$Following [51], an efficient tSE NIZK for the above relation can be obtained under the DLIN assumption by combining classical Groth–Sahai NIZKs [74, 75] with Cramer–Shoup encryption [38]. We leave the count of the exact number of group elements as an exercise to the reader.
5 Application to Tamper-Resilient Security
In this section we revisit the classical application of non-malleable codes to protecting arbitrary cryptographic primitives against memory-tampering attacks [55, 56, 84], highlighting in particular the benefits that our new notion of continuous non-malleability brings to the picture.
In what follows, let \(\textsf {F}(\kappa ,\cdot )\) be an efficiently computable functionality taking a secret key \(\kappa \in \{0,1\}^{k}\) and value \(x\in \{0,1\}^{*}\) as input, and producing some output \(y\in \{0,1\}^{*}\). We are concerned about attackers changing the original key \(\kappa \) into a related key \(\tilde{\kappa }\), and observing the effect of such changes at the output. For concreteness, we will focus on the setting in which the key material is stored into two separate parts of the memory that can be tampered independently, but the results in this section can be easily extended to general tampering (parameterized by a tampering family supported by the non-malleable code). As explained below, we distinguish between stateless and stateful functionalities.
5.1 Stateless Functionalities
In the case of stateless functionalities, the key \(\kappa \) is fixed once and for all. The main idea is to transform the original functionality \(\textsf {F}\) into some kind of “hardened” functionality \(\hat{\textsf {F}}\) using a non-malleable code \(\Gamma \) to encode the key. Previous transformations aiming at protecting stateless functionalities [55, 56, 84] required to freshly re-encode the key \(\kappa \) each time the functionality is invoked. Our approach avoids the re-encoding of the key at each invocation, leading to a stateless transformation. This solves an open question from [55, 56]. Moreover, we consider a setting where the encoded key is stored into a memory \({\mathcal {M}}:= ({\mathcal {M}} _0,{\mathcal {M}} _1)\) which is much larger than the size needed to store the encoding itself (say \(|{\mathcal {M}} _0| = |{\mathcal {M}} _1| = p(n)\) where \(p(n)\) is polynomial in the length n of the encoding). When (perfect) erasures are not possible, this feature naturally allows the adversary to make copies of the initial encoding and tamper continuously with it.
Let us formally define what it means to harden a stateless functionality.
Definition 8
(Stateless hardened functionality) Let \(\Gamma = (\textsf {Init},\textsf {Enc},\textsf {Dec})\) be a split-state code in the CRS model, with k-bit messages and 2n-bit codewords. Let \(\textsf {F}:\{0,1\}^{k}\times \{0,1\}^{*}\rightarrow \{0,1\}^{*}\) be a stateless functionality, and \(\delta \in \{0,1\}\) be a public value. We define a stateless hardened functionality \(\hat{\textsf {F}}^\Gamma :=\hat{\textsf {F}}:\{0,1\}^{2p}\times \{0,1\}^{*}\rightarrow \{0,1\}^{*}\) with \(p= \texttt {poly}(n)\) as a tuple of algorithms \((\textsf {Setup},\textsf {MemCompile},\textsf {Exec})\) described as follows:
-
 : Sample
: Sample 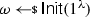 , initialize \(\delta = 0\), and return \({\hat{\omega }}= (\omega ,\delta )\).
, initialize \(\delta = 0\), and return \({\hat{\omega }}= (\omega ,\delta )\). -
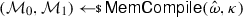 : Let
: Let  . Parse \({\hat{\omega }}= (\omega ,\delta )\). For \(\beta \in \{0,1\}\), store \(c_\beta \) in the first n bits of \({\mathcal {M}} _\beta \); the remaining bits of \({\mathcal {M}} _\beta \) are set to \(0^{p-n}\). Define \({\mathcal {M}}:= ({\mathcal {M}} _0,{\mathcal {M}} _1)\).
. Parse \({\hat{\omega }}= (\omega ,\delta )\). For \(\beta \in \{0,1\}\), store \(c_\beta \) in the first n bits of \({\mathcal {M}} _\beta \); the remaining bits of \({\mathcal {M}} _\beta \) are set to \(0^{p-n}\). Define \({\mathcal {M}}:= ({\mathcal {M}} _0,{\mathcal {M}} _1)\). -
 : Parse \({\hat{\omega }}= (\omega ,\delta )\). In case \(\delta = 1\) output \(\bot \); else, let \(\tilde{c}_\beta = {\mathcal {M}} _\beta [1,\ldots ,n]\) for \(\beta \in \{0,1\}\). Run \(\tilde{\kappa }= \textsf {Dec}(\omega ,(\tilde{c}_0,\tilde{c}_1))\): If \(\tilde{\kappa }= \bot \), then output \(\bot \) and set \(\delta = 1\). Else, output
: Parse \({\hat{\omega }}= (\omega ,\delta )\). In case \(\delta = 1\) output \(\bot \); else, let \(\tilde{c}_\beta = {\mathcal {M}} _\beta [1,\ldots ,n]\) for \(\beta \in \{0,1\}\). Run \(\tilde{\kappa }= \textsf {Dec}(\omega ,(\tilde{c}_0,\tilde{c}_1))\): If \(\tilde{\kappa }= \bot \), then output \(\bot \) and set \(\delta = 1\). Else, output  . Finally, update the CRS to \({\hat{\omega }}:= (\omega ,\delta )\).
. Finally, update the CRS to \({\hat{\omega }}:= (\omega ,\delta )\).
Remark 1
(On \(\delta \)) The public value \(\delta \) is just a way how to implement the self-destruct feature. An alternative approach would be to let the hardened functionality simply output a dummy value and overwrite \(({\mathcal {M}} _0,{\mathcal {M}} _1)\) with the all-zero string. As we do not want to assume perfect erasures, we use the first approach here.
Note that we assume that \(\delta \) is untamperable and one-time writable. The latter is necessary, as an adversary tampering with \(\delta \) could always switch-off the self-destruct feature and apply a variant of the attack from [70] to recover the secret state.
Similarly to [55, 56, 84], security of \(\hat{\textsf {F}}\) is defined via the comparison of a real and an ideal experiment. The real experiment features an adversary \({\textsf {A}}\) interacting with \(\hat{\textsf {F}}\); the adversary is allowed to honestly run the functionality on any chosen input, but also to modify the memory and retrieve a bounded amount of information from it. The ideal experiment features a simulator \(\textsf {S}\) that is given black-box access to the original functionality \(\textsf {F}\) and to the adversary \({\textsf {A}}\), but is not allowed any tampering or leakage query. The two experiments are formally described below.
Experiment \(\mathbf{Real} _{\hat{\textsf {F}},{\textsf {A}}}(\lambda ,\kappa )\). First  and
and  are run, and \({\hat{\omega }}\) is given to \({\textsf {A}}\). Then, \({\textsf {A}}\) can issue the following commands polynomially many times (in any order):
are run, and \({\hat{\omega }}\) is given to \({\textsf {A}}\). Then, \({\textsf {A}}\) can issue the following commands polynomially many times (in any order):
-
\(\langle \texttt {Leak},(g_{0}^{(j)}, g_{1}^{(j)})\rangle \): In response to the j-th leakage query compute \(\Lambda _{0}^{(j)} = g_{0}^{(j)}({\mathcal {M}} _0)\) and \(\Lambda _{1}^{(j)} = g_{1}^{(j)}({\mathcal {M}} _1)\), and output \(\Lambda ^{(j)}:=(\Lambda _{0}^{(j)},\Lambda _{1}^{(j)})\).
-
\(\langle \texttt {Tamper},(f_{0}^{(j)}, f_{1}^{(j)})\rangle \): In response to the j-th tampering query compute \({\widetilde{{\mathcal {M}}}}_0 = f_{0}^{(j)}({\mathcal {M}} _0)\) and \({{\widetilde{{\mathcal {M}}}}}_1 = f_{1}^{(j)}({\mathcal {M}} _1)\), and replace \({\mathcal {M}} =({\mathcal {M}} _0,{\mathcal {M}} _1)\) with \({{\widetilde{{\mathcal {M}}}}}=({{\widetilde{{\mathcal {M}}}}}_0,{{\widetilde{{\mathcal {M}}}}}_1)\).
-
\(\langle \texttt {Eval}, x^{(j)}\rangle \): In response to the j-th evaluation query run
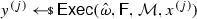 : If \(y^{(j)} = \bot \), output \(\bot \) and self-destruct; else, output \(y^{(j)}\).
: If \(y^{(j)} = \bot \), output \(\bot \) and self-destruct; else, output \(y^{(j)}\).
At the end of the experiment, \({\textsf {A}}\) outputs a bit that is an arbitrary function of its view (and this is also the output of the experiment).
Experiment \(\mathbf{Ideal} _{\textsf {F},{\textsf {A}},\textsf {S}}(\lambda ,\kappa )\). The simulator sets up the CRS \({\hat{\omega }}= (\omega ,\delta )\) and is given black-box access to the functionality \(\textsf {F}(\kappa ,\cdot )\) and the adversary \({\textsf {A}}\). At the end of the experiment, \({\textsf {A}}\) outputs a bit that is an arbitrary function of its view (and this is also the output of the experiment).
Definition 9
(Continuous tamper simulatability) Let \(\Gamma \) be a split-state encoding scheme in the CRS model and consider a stateless functionality \(\textsf {F}\) with corresponding hardened functionality \(\hat{\textsf {F}}:= \hat{\textsf {F}}^\Gamma \). We say that \(\Gamma \) is \(\ell \)-leakage continuously tamper simulatable in the split-state model (for stateless functionalities), if for all PPT adversaries \({\textsf {A}}\) leaking at most \(\ell \) bits from each memory part, there exists a PPT simulator \(\textsf {S}\) such that for any initial state \(\kappa \in \{0,1\}^k\):
The theorem below says that any continuously non-malleable split-state code is automatically continuously tamper simulatable.
Theorem 4
Let \(\Gamma \) be any \(\ell \)-leakage-resilient continuously superFootnote 18 non-malleable split-state code in the CRS model. Then \(\Gamma \) is \(\ell \)-leakage continuously tamper simulatable in the split-state model (for stateless functionalities).
Proof
Consider the following simulator \(\textsf {S}\). At the outset, \(\textsf {S}\) samples  and sets \(\delta = 0\), yielding \({\hat{\omega }}= (\omega ,\delta )\). Then, it samples a random encoding of zero, namely
and sets \(\delta = 0\), yielding \({\hat{\omega }}= (\omega ,\delta )\). Then, it samples a random encoding of zero, namely  and sets \({\mathcal {M}} _\beta [1,\ldots ,n] := c_\beta \) for \(\beta \in \{0,1\}\). The remaining bits of \(({\mathcal {M}} _0,{\mathcal {M}} _1)\) are set to \(0^{p- n}\). Next, \(\textsf {S}\) runs \({\textsf {A}}(1^\lambda ,{\hat{\omega }})\) and answers to its queries alternating between the following two modes (starting with the normal mode):
and sets \({\mathcal {M}} _\beta [1,\ldots ,n] := c_\beta \) for \(\beta \in \{0,1\}\). The remaining bits of \(({\mathcal {M}} _0,{\mathcal {M}} _1)\) are set to \(0^{p- n}\). Next, \(\textsf {S}\) runs \({\textsf {A}}(1^\lambda ,{\hat{\omega }})\) and answers to its queries alternating between the following two modes (starting with the normal mode):
-
Normal Mode. Given state \(({\mathcal {M}} _0,{\mathcal {M}} _1)\), while \({\textsf {A}}\) continues issuing queries, answer as follows:
-
\(\langle \texttt {Leak},(g_{0}^{(j)}, g_{1}^{(j)})\rangle \): Upon input the j-th leakage query, compute \(\Lambda _\beta ^{(j)} = g_{\beta }^{(j)}({\mathcal {M}} _\beta )\) for \(\beta \in \{0,1\}\), and reply with \((\Lambda _0^{(j)},\Lambda _1^{(j)})\).
-
\(\langle \texttt {Tamper}, (f_{0}^{(j)}, f_{1}^{(j)})\rangle \): Upon input the j-th tampering query, compute \({{\widetilde{{\mathcal {M}}}}}_\beta = f_{\beta }^{(j)}({\mathcal {M}} _\beta )\) for \(\beta \in \{0,1\}\). Let \((\tilde{c}_0,\tilde{c}_1) := ({{\widetilde{{\mathcal {M}}}}}_{0}[1,\ldots ,n],{{\widetilde{{\mathcal {M}}}}}_{1}[1,\ldots ,n])\). If \((\tilde{c}_0,\tilde{c}_1) = (c_0,c_1)\), continue in the current mode. Else, go to the overwritten mode with state \(({\mathcal {M}} _0,{\mathcal {M}} _1) := ({{\widetilde{{\mathcal {M}}}}}_0,{{\widetilde{{\mathcal {M}}}}}_1)\), and, if \(\textsf {Dec}(\omega ,(\tilde{c}_0,\tilde{c}_1)) = \bot \), update the CRS to \({\hat{\omega }}:= (\omega ,1)\).
-
\(\langle \texttt {Eval}, x^{j}\rangle \): Upon input the j-th evaluation query, invoke \(\textsf {F}(\kappa ,\cdot )\) to get
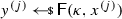 and reply with \(y^{(j)}\).
and reply with \(y^{(j)}\).
-
-
Overwritten Mode. Given state \({\mathcal {M}}:=({\mathcal {M}} _0,{\mathcal {M}} _1)\), while \({\textsf {A}}\) continues issuing queries, answer as follows:
-
\(\langle \texttt {Leak},(g_{0}^{(j)}, g_{1}^{(j)})\rangle \): Upon input the j-th leakage query, compute \(\Lambda _\beta ^{(j)} = g_{\beta }^{(j)}({\mathcal {M}} _\beta )\) for \(\beta \in \{0,1\}\), and reply with \((\Lambda _0^{(j)},\Lambda _1^{(j)})\).
-
\(\langle \texttt {Tamper}, (f_{0}^{(j)}, f_{1}^{(j)})\rangle \): Upon input the j-th tampering query \((f_{0}^{(j)}, f_{1}^{(j)})\), compute \({{\widetilde{{\mathcal {M}}}}}_\beta = f_{\beta }^{(j)}({\mathcal {M}} _\beta )\) for \(\beta \in \{0,1\}\). Let \((\tilde{c}_0,\tilde{c}_1) := ({{\widetilde{{\mathcal {M}}}}}_{0}[1,\ldots ,n],{{\widetilde{{\mathcal {M}}}}}_{1}[1,\ldots ,n])\). If \((\tilde{c}_0,\tilde{c}_1) = (c_0,c_1)\), go to the normal mode with state \(({\mathcal {M}} _0,{\mathcal {M}} _1) := ({{\widetilde{{\mathcal {M}}}}}_0,{{\widetilde{{\mathcal {M}}}}}_1)\). Else, continue in the current mode, and, if \(\textsf {Dec}(\omega ,(\tilde{c}_0,\tilde{c}_1)) = \bot \), update the CRS to \({\hat{\omega }}:= (\omega ,1)\).
-
\(\langle \texttt {Eval}, x^{(j)}\rangle \): Upon input the j-th evaluation query, run
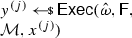 and reply with \(y^{(j)}\).
and reply with \(y^{(j)}\).
-
Intuitively, since the code is non-malleable, the adversary can either keep the encoding of the secret key unchanged or overwrite it with the encoding of an unrelated value. These two cases are captured in the above modes: The simulator starts in the normal mode and then, whenever the adversary modifies the initial encoding, it switches to the overwritten mode. However, note that the adversary can use the extra space to keep a copy of the original encoding and place it back at some later point in time. When this happens, the simulator switches back to the normal mode; this feature is important to maintain simulation.
By contradiction, assume that there exists a PPT attacker \({\textsf {A}}\), and some key \(\kappa \in \{0,1\}^{k}\), such that the following holds for the above defined simulator \(\textsf {S}\):
We build a PPT attacker \({\textsf {A}}'\) breaking continuous non-malleability of the code \(\Gamma \). A description of \({\textsf {A}}'\) follows:
\(\underline{\hbox {Attacker }{\textsf {A}}'\hbox { for }(\textsf {Init},\textsf {Enc},\textsf {Dec}):}\)
- 1.
Upon receiving the CRS \(\omega \), forward \((m_0 := \kappa ,m_1 := 0^k)\) to the challenger.
- 2.
Initialize \(\tilde{\kappa }:= \varepsilon \), and \(\mathtt {mode}\) to \(\mathtt {normal}\). Set \(\delta =0\), and pass \({\hat{\omega }}:= (\omega ,\delta )\) to \({\textsf {A}}\).
- 3.
Upon input a command \(\langle \texttt {Tamper}, (f_{0}^{(j)}, f_{1}^{(j)})\rangle \) from \({\textsf {A}}\), define the functions \(f_\mathsf{pad}:\{0,1\}^n\rightarrow \{0,1\}^p\) and \(f_\mathsf{cut}: \{0,1\}^p\rightarrow \{0,1\}^n\) as \(f_\mathsf{pad}(x) = (x||0^{p-n})\) and \(f_\mathsf{cut}(x||x') = x\), for any \(x \in \{0,1\}^n\) and \(x'\in \{0,1\}^{p-n}\). Query the tampering oracle \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),\cdot )\) with the pair of functions \(({\hat{f}_{0}}^{(j)},{\hat{f}_{1}}^{(j)})\), where for each \(\beta \in \{0,1\}\) function \({\hat{f}}_{\beta }^{(j)}\) is defined as
$$\begin{aligned} {\hat{f}}_{\beta }^{(j)}(\cdot ) := f_\mathsf{cut}\circ f_{\beta }^{(j)}\circ f_{\beta }^{(j-1)}\circ \cdots \circ f_{\beta }^{(1)}\circ f_\mathsf{pad}(\cdot ). \end{aligned}$$(2)Then:
If the oracle returns \(\bot \), update the CRS to \({{\hat{\omega }}} := (\omega ,1)\).
If the oracle returns \(\diamond \), set \(\mathtt {mode}\) to \(\mathtt {normal}\).
If the oracle returns a codeword \(\tilde{c}^{(j)}:=(\tilde{c}_0^{(j)},\tilde{c}_1^{(j)})\), set \(\mathtt {mode}\) to \(\mathtt {overwritten}\) and overwrite \(\tilde{\kappa }:= \textsf {Dec}(\omega ,(\tilde{c}_0^{(j)},\tilde{c}_1^{(j)}))\).
- 4.
Upon input a command \(\langle \texttt {Leak},(g_{0}^{(j)}, g_{1}^{(j)})\rangle \) from \({\textsf {A}}\), query oracle \({\mathcal {O}}_\textsf {leak}^\ell (c_0,\cdot )\) and \({\mathcal {O}}_\textsf {leak}^\ell (c_1,\cdot )\) with functions \({\hat{g}_{0}}^{(j)}\) and \({\hat{g}_{1}}^{(j)}\), where for each \(\beta \in \{0,1\}\) function \({\hat{g}}_{\beta }^{(j)}\) is defined as
$$\begin{aligned} {\hat{g}}_{\beta }^{(j)}(\cdot ) := g_{\beta }^{(j)}\circ f_{\beta }^{(i)}\circ \cdots \circ f_{\beta }^{(1)}\circ f_\mathsf{pad}(\cdot ), \end{aligned}$$(3)where i is the index of the last tampering query. Then, forward the answer \((\Lambda _0^{(j)},\Lambda _1^{(j)})\) to \({\textsf {A}}\).
- 5.
Upon input a command \(\langle \texttt {Eval},x^{(j)}\rangle \) from \({\textsf {A}}\), if \(\delta =1\) return \(\bot \) to \({\textsf {A}}\). Else, proceed as follows:
If \(\mathtt {mode} = \mathtt {normal}\), let
and return \(y^{(j)}\) to \({\textsf {A}}\).
Else, if \(\mathtt {mode} = \mathtt {overwritten}\), let
and return \(y^{(j)}\) to \({\textsf {A}}\).
- 6.
Upon receiving a guess \(b'\) from \({\textsf {A}}\), output \(b'\) and terminate.
For the analysis, first note that \({\textsf {A}}'\) runs in polynomial time. Next, we claim that the simulation done by \({\textsf {A}}'\) is perfect. This is because:
-
The CRS \({\hat{\omega }}\) is distributed identically to the CRS in \(\mathbf{Real} _{\hat{\textsf {F}},{\textsf {A}},\kappa }(\lambda )\) and \(\mathbf{Ideal} _{\textsf {F},{\textsf {A}},\textsf {S},\kappa }(\lambda )\).
-
Depending on the target encoding \((c_0,c_1)\) being either an encoding of \(\kappa \) or an encoding of \(0^k\), the queries of \({\textsf {A}}\) are answered exactly as in \(\mathbf{Real} _{\hat{\textsf {F}},{\textsf {A}},\kappa }(\lambda )\) or in \(\mathbf{Ideal} _{\textsf {F},{\textsf {A}},\textsf {S},\kappa }(\lambda )\). More precisely:
-
Tampering queries are handled using the oracle \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),\cdot )\). However, note that \({\textsf {A}}'\) cannot directly forward the tampering functions \((f_0^{(j)},f_1^{(j)})\) to this oracle. In fact: (i) Each of \(f_0^{(j)},f_1^{(j)}\) maps p bits into p bits, whereas \({\textsf {A}}'\)’s tampering oracle expects functions mapping n bits into n bits; (ii) In both \(\mathbf{Real} _{\hat{\textsf {F}},{\textsf {A}},\kappa }(\lambda )\) and \(\mathbf{Ideal} _{\textsf {F},{\textsf {A}},\textsf {S},\kappa }(\lambda )\) the tampering functions are applied to the current memory content \(({\mathcal {M}} _0,{\mathcal {M}} _1)\), whereas the tampering oracle always uses the target codeword \((c_0,c_1)\). However, the reduction can easily handle this mismatch by padding each part of the target codeword with zeroes, recover the current memory, and define the tampered codeword to be the first n bits of \({{\widetilde{{\mathcal {M}}}}}_0 := f_0^{(j)}({\mathcal {M}} _0)\) and \({{\widetilde{{\mathcal {M}}}}}_1 := f_1^{(j)}({\mathcal {M}} _1)\) (cf. Eq. (2)).
-
Leakage queries are handled using the oracles \({\mathcal {O}}_\textsf {leak}^\ell (c_0,\cdot )\) and \({\mathcal {O}}_\textsf {leak}^\ell (c_1,\cdot )\). By a similar argument as above, the reduction perfectly emulates such queries by adjusting them as in Eq. (3). Furthermore, if \({\textsf {A}}\) leaks at most \(\ell \) bits from each side of the memory, \({\textsf {A}}'\) leaks at most \(\ell \) bits from each side of the target codeword.
-
Evaluation queries are perfectly emulated. Indeed, whenever \(\mathtt {mode}\) equals \(\mathtt {normal}\), the reduction answers evaluation queries by running \(\textsf {F}\) on key \(\kappa \) (this corresponds to the normal mode of simulator \(\textsf {S}\)). Similarly, whenever \(\mathtt {mode}\) equals \(\mathtt {overwritten}\), the reduction answers evaluation queries by running \(\textsf {F}\) on the current tampered key \(\tilde{\kappa }\) which results from applying the tampering functions to the initial memory (this corresponds to the overwritten mode of simulator \(\textsf {S}\)).
-
It follows that in case \((c_0,c_1)\) is an encoding of \(\kappa \), the reduction perfectly emulates the view of \({\textsf {A}}\) in \(\mathbf{Real} _{\hat{\textsf {F}},{\textsf {A}},\kappa }(\lambda )\). Similarly, when \((c_0,c_1)\) is an encoding of \(0^k\), the reduction perfectly emulates the view of \({\textsf {A}}\) in \(\mathbf{Ideal} _{\hat{\textsf {F}},\textsf {S}{\textsf {A}},\kappa }(\lambda )\). Hence, Eq. (1) implies
a contradiction. \(\square \)
5.2 Stateful Functionalities
In the case of stateful functionalities, the function \(\textsf {F}\) has a secret state \(\sigma \) that is updated at each invocation, i.e.,  . As the state gets updated, in this setting we inherently need to re-encode the new state after each execution.
. As the state gets updated, in this setting we inherently need to re-encode the new state after each execution.
Furthermore, since we do not assume erasures in our model, the following subtlety arises. An adversary can first copy some old (encoded) state to a different part of the memory, and later replace the current (encoded) state by the old one. This essentially corresponds to a reset attack, that cannot be simulated given only black-box access to the original functionality. To overcome this obstacle, our transformation leverages an untamperable public counter \(\gamma \in {\mathbb {N}}\) that helps us detecting whenever the functionality is reset to a previous state, in which case a self-destruct is triggered; note that such a counter can be implemented using \(\log (\lambda )\) bits (plus the additional bit to implement the self-destruct mechanism).Footnote 19
Below, we define what it means to harden a stateful functionality.
Definition 10
(Stateful hardened functionality) Let \(\Gamma = (\textsf {Init},\textsf {Enc},\textsf {Dec})\) be a split-state code in the CRS model, with \((k + \log (\lambda ))\)-bit messages and 2n-bit codewords. Let \(\textsf {F}:\{0,1\}^{k}\times \{0,1\}^{*}\rightarrow \{0,1\}^{k}\times \{0,1\}^{*}\) be a stateful functionality, \(\delta \in \{0,1\},\gamma \in \{0,1\}^\lambda \) be a public values. We define a stateful hardened functionality \(\hat{\textsf {F}}^\Gamma :=\hat{\textsf {F}}:\{0,1\}^{2p}\times \{0,1\}^{*}\rightarrow \{0,1\}^{2p}\times \{0,1\}^{*}\) where \(p= \texttt {poly}(n)\) as a tuple of algorithms \((\textsf {Setup}, \textsf {MemCompile}, \textsf {Exec})\) described as follows:
-
 : Sample
: Sample 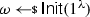 , initialize \((\gamma ,\delta ) = (1,0)\), and return \({\hat{\omega }}:= (\omega ,\gamma ,\delta )\).
, initialize \((\gamma ,\delta ) = (1,0)\), and return \({\hat{\omega }}:= (\omega ,\gamma ,\delta )\). -
 : Parse \({\hat{\omega }}= (\omega ,\gamma ,\delta )\). Let
: Parse \({\hat{\omega }}= (\omega ,\gamma ,\delta )\). Let 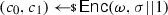 . For \(\beta \in \{0,1\}\), store \(c_\beta \) in the first n bits of \({\mathcal {M}} _\beta \); the remaining bits of \({\mathcal {M}} _\beta \) are set to \(0^{p-n}\). Define \({\mathcal {M}}:= ({\mathcal {M}} _0,{\mathcal {M}} _1)\).
. For \(\beta \in \{0,1\}\), store \(c_\beta \) in the first n bits of \({\mathcal {M}} _\beta \); the remaining bits of \({\mathcal {M}} _\beta \) are set to \(0^{p-n}\). Define \({\mathcal {M}}:= ({\mathcal {M}} _0,{\mathcal {M}} _1)\). -
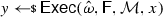 : Parse \({\hat{\omega }}= (\omega ,\gamma ,\delta )\). In case \(\delta = 1\) output \(\bot \); else, let \(\tilde{c}_\beta = {\mathcal {M}} _\beta [1,\ldots ,n]\) for \(\beta \in \{0,1\}\). Run \(\tilde{\sigma }||\tilde{\gamma }= \textsf {Dec}(\omega ,(\tilde{c}_0,\tilde{c}_1))\): If either \(\tilde{\sigma }= \bot \) or \(\tilde{\gamma }\ne \gamma \), then output \(\bot \) and set \(\delta = 1\). Else, output y such that
: Parse \({\hat{\omega }}= (\omega ,\gamma ,\delta )\). In case \(\delta = 1\) output \(\bot \); else, let \(\tilde{c}_\beta = {\mathcal {M}} _\beta [1,\ldots ,n]\) for \(\beta \in \{0,1\}\). Run \(\tilde{\sigma }||\tilde{\gamma }= \textsf {Dec}(\omega ,(\tilde{c}_0,\tilde{c}_1))\): If either \(\tilde{\sigma }= \bot \) or \(\tilde{\gamma }\ne \gamma \), then output \(\bot \) and set \(\delta = 1\). Else, output y such that 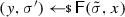 , run
, run 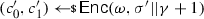 , and for each \(\beta \in \{0,1\}\) write \(c_\beta '\) in the first n bits of \({\mathcal {M}} _\beta \). Finally, update the CRS to \({\hat{\omega }}:= (\omega ,\gamma +1,\delta )\).
, and for each \(\beta \in \{0,1\}\) write \(c_\beta '\) in the first n bits of \({\mathcal {M}} _\beta \). Finally, update the CRS to \({\hat{\omega }}:= (\omega ,\gamma +1,\delta )\).
Remark 2
(On \((\gamma ,\delta )\)) As in the case of stateless functionalities, we require \(\delta \) to be untamperable and one-time writable (cf. Remark 1). Moreover, the counter \(\gamma \) is assumed to be untamperable and poly-time writable. The latter is necessary, as otherwise the attacker can use the extra memory to reset the functionality to a previous valid state, which cannot be simulated with black-box access to the original functionality.
Security of a stateful hardened functionality is defined analogously to the stateless case (cf. Definition 9). We show the following result:
Theorem 5
Let \(\Gamma \) be any \(\ell \)-leakage-resilient continuously super non-malleable split-state code in the CRS model. Then \(\Gamma \) is \(\ell \)-leakage continuously tamper simulatable in the split-state model (for stateful functionalities).
Proof
Similarly to the proof of Theorem 4, we describe a simulator \(\textsf {S}\) running in experiment \(\mathbf{Ideal} _{\textsf {F},{\textsf {A}},\textsf {S}}(\lambda ,\sigma )\) which simulates the view of adversary \({\textsf {A}}\) in the experiment \(\mathbf{Real} _{\hat{\textsf {F}},{\textsf {A}}}(\lambda ,\sigma )\) for every possible initial state \(\sigma \in \{0,1\}^k\). As usual, the simulator \(\textsf {S}\) is given black-box access to \({\textsf {A}}\) (which can issue \(\texttt {Tamper}\), \(\texttt {Leak}\), and \(\texttt {Eval}\) commands), and to the reactive functionality \(\textsf {F}(\sigma ,\cdot )\) with initial state \(\sigma \). In order to simplify the simulator, we are going to assume that the attacker \({\textsf {A}}\) issues commands in rounds, where each round consist exactly of one leakage query, one tampering query, and one execute query (in this order). A generalization is straightforward.
At the outset, \(\textsf {S}\) samples  and sets \((\gamma ,\delta ) = (1,0)\), yielding \({\hat{\omega }}:= (\omega ,\gamma ,\delta )\). Next, \(\textsf {S}\) runs \({\textsf {A}}(1^\lambda ,{\hat{\omega }})\) and answers to its queries using the following two modes (starting with the normal mode):
and sets \((\gamma ,\delta ) = (1,0)\), yielding \({\hat{\omega }}:= (\omega ,\gamma ,\delta )\). Next, \(\textsf {S}\) runs \({\textsf {A}}(1^\lambda ,{\hat{\omega }})\) and answers to its queries using the following two modes (starting with the normal mode):
-
Normal Mode. Given state \(({\mathcal {M}} _0,{\mathcal {M}} _1)\), while \({\textsf {A}}\) continues issuing queries, answer as follows:
-
Sample
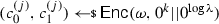 , and let \({\mathcal {M}} _\beta [1,\ldots ,n] := c_\beta \) for \(\beta \in \{0,1\}\). If \(j=1\) (i.e., during the first round), the remaining bits of \(({\mathcal {M}} _0,{\mathcal {M}} _1)\) are set to \(0^{p- n}\).
, and let \({\mathcal {M}} _\beta [1,\ldots ,n] := c_\beta \) for \(\beta \in \{0,1\}\). If \(j=1\) (i.e., during the first round), the remaining bits of \(({\mathcal {M}} _0,{\mathcal {M}} _1)\) are set to \(0^{p- n}\). -
\(\langle \texttt {Leak},(g_{0}^{(j)}, g_{1}^{(j)})\rangle \): Upon input the j-th leakage query, compute \(\Lambda _\beta ^{(j)} = g_{\beta }^{(j)}({\mathcal {M}} _\beta )\) for \(\beta \in \{0,1\}\), and reply with \((\Lambda _0^{(j)},\Lambda _1^{(j)})\).
-
\(\langle \texttt {Tamper}, (f_{0}^{(j)}, f_{1}^{(j)})\rangle \): Upon input the j-th tampering query, compute \({{\widetilde{{\mathcal {M}}}}}_\beta = f_{\beta }^{(j)}({\mathcal {M}} _\beta )\) for \(\beta \in \{0,1\}\). Let \((\tilde{c}_0,\tilde{c}_1) := ({{\widetilde{{\mathcal {M}}}}}_{0}[1,\ldots ,n],{{\widetilde{{\mathcal {M}}}}}_{1}[1,\ldots ,n])\). If \((\tilde{c}_0,\tilde{c}_1) = (c_0^{(j)},c_1^{(j)})\), continue in the current mode. Else, go to the overwritten mode with state \(({\mathcal {M}} _0,{\mathcal {M}} _1) := ({{\widetilde{{\mathcal {M}}}}}_0,{{\widetilde{{\mathcal {M}}}}}_1)\), and, if \(\textsf {Dec}(\omega ,(\tilde{c}_0,\tilde{c}_1)) \in \{\bot ,\tilde{\sigma }||\tilde{\gamma }\}\) for some \(\tilde{\gamma }\ne \gamma \), update the CRS to \({\hat{\omega }}:= (\omega ,\gamma ,1)\).
-
\(\langle \texttt {Eval}, x^{(j)}\rangle \): Upon input the j-th evaluation query, invoke \(\textsf {F}(\sigma ,\cdot )\) to obtain \(y^{(j)}\) s.t.
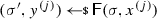 , where \(\sigma \) is the current state of the functionality and \(\sigma '\) is the new stateFootnote 20 (which is unknown to \(\textsf {S}\)), and reply with \(y^{(j)}\). Update the CRS to \({\hat{\omega }}:= (\omega ,\gamma +1,\delta )\).
, where \(\sigma \) is the current state of the functionality and \(\sigma '\) is the new stateFootnote 20 (which is unknown to \(\textsf {S}\)), and reply with \(y^{(j)}\). Update the CRS to \({\hat{\omega }}:= (\omega ,\gamma +1,\delta )\).
-
-
Overwritten Mode. Given state \({\mathcal {M}}:=({\mathcal {M}} _0,{\mathcal {M}} _1)\), while \({\textsf {A}}\) continues issuing queries, answer as follows:
-
\(\langle \texttt {Leak},(g_{0}^{(j)}, g_{1}^{(j)})\rangle \): Upon input the j-th leakage query, compute \(\Lambda _\beta ^{(j)} = g_{\beta }^{(j)}({\mathcal {M}} _\beta )\) for \(\beta \in \{0,1\}\), and reply with \((\Lambda _0^{(j)},\Lambda _1^{(j)})\).
-
\(\langle \texttt {Tamper}, (f_{0}^{(j)}, f_{1}^{(j)})\rangle \): Upon input the j-th tampering query \((f_{0}^{(j)}, f_{1}^{(j)})\), compute \({{\widetilde{{\mathcal {M}}}}}_\beta = f_{\beta }^{(j)}({\mathcal {M}} _\beta )\) for \(\beta \in \{0,1\}\). Let \((\tilde{c}_0,\tilde{c}_1) := ({{\widetilde{{\mathcal {M}}}}}_{0}[1,\ldots ,n],{{\widetilde{{\mathcal {M}}}}}_{1}[1,\ldots ,n])\). Continue in the current mode with state \(({\mathcal {M}} _0,{\mathcal {M}} _1) := ({{\widetilde{{\mathcal {M}}}}}_0,{{\widetilde{{\mathcal {M}}}}}_1)\), and, if \(\textsf {Dec}(\omega ,(\tilde{c}_0,\tilde{c}_1)) \in \{\bot ,\tilde{\sigma }||\tilde{\gamma }\}\) for some \(\tilde{\gamma }\ne \gamma \), update the CRS to \({\hat{\omega }}:= (\omega ,\gamma ,1)\).
-
\(\langle \texttt {Eval}, x^{(j)}\rangle \): Upon input the j-th evaluation query, run
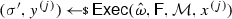 and reply with \(y^{(j)}\). Compute
and reply with \(y^{(j)}\). Compute 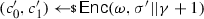 , and update the first n bits of \({\mathcal {M}} _\beta \) to \(c_\beta \) for each \(\beta \in \{0,1\}\), and the CRS to \({\hat{\omega }}:= (\omega ,\gamma +1,\delta )\).
, and update the first n bits of \({\mathcal {M}} _\beta \) to \(c_\beta \) for each \(\beta \in \{0,1\}\), and the CRS to \({\hat{\omega }}:= (\omega ,\gamma +1,\delta )\).
-
The intuition behind the above simulation strategy is similar to that in the proof of Theorem 4. One important difference is the fact that, after the simulator switches to the overwritten mode, it never goes back to the normal mode. Intuitively, this is because the untamperable counter ensures that the attacker can never copy an old state back to the first part of the memory. A further difficulty in the analysis is that in the case of stateful functionalities the state is re-encoded after each invocation, and thus we cannot directly reduce to the security of the underlying continuously non-malleable code.
Experiment \(\mathbf{Hyb} ^{(i)}_{\textsf {F},{\textsf {A}},\textsf {S}}(\lambda ,\sigma )\). In order to overcome the above difficulty, we consider a sequence of mental experiments. Let \(q \in \texttt {poly}(\lambda )\) be an upper bound on the total number of queries (and thus rounds). For all \(i \in [q]\), consider the following hybrid experiment where the simulator runs a modified normal mode and the same overwritten mode.
-
First
 is run, and \({\hat{\omega }}\) is given to \({\textsf {A}}\).
is run, and \({\hat{\omega }}\) is given to \({\textsf {A}}\). -
For the first i rounds, \({\textsf {A}}\)’s commands are answered exactly as in experiment \(\mathbf{Ideal} _{\textsf {F},{\textsf {A}},\textsf {S}}(\lambda ,\sigma )\).
-
Starting from round \(i+1\), if the simulator \(\textsf {S}\) is already in the overwritten mode, then continue simulating as in the ideal world. Otherwise, proceed with the following modified normal mode:
-
Sample
 , and let \({\mathcal {M}} _\beta [1,\ldots ,n] := c_\beta \) for \(\beta \in \{0,1\}\). If \(j=1\) (i.e., during the first round), the remaining bits of \(({\mathcal {M}} _0,{\mathcal {M}} _1)\) are set to \(0^{p- n}\).
, and let \({\mathcal {M}} _\beta [1,\ldots ,n] := c_\beta \) for \(\beta \in \{0,1\}\). If \(j=1\) (i.e., during the first round), the remaining bits of \(({\mathcal {M}} _0,{\mathcal {M}} _1)\) are set to \(0^{p- n}\). -
\(\langle \texttt {Leak},(g_{0}^{(j)}, g_{1}^{(j)})\rangle \): As in the ideal world.
-
\(\langle \texttt {Tamper}, (f_{0}^{(j)}, f_{1}^{(j)})\rangle \): As in the ideal world.
-
\(\langle \texttt {Eval}, x^{(j)}\rangle \): Upon input the j-th evaluation query, run
 where \(\sigma \) is the current state of the functionality and \(\sigma '\) is the new state, and reply with \(y^{(j)}\). Redefine \(\sigma := \sigma '\), and update the CRS to \({\hat{\omega }}:= (\omega ,\gamma := \gamma +1,\delta )\).
where \(\sigma \) is the current state of the functionality and \(\sigma '\) is the new state, and reply with \(y^{(j)}\). Redefine \(\sigma := \sigma '\), and update the CRS to \({\hat{\omega }}:= (\omega ,\gamma := \gamma +1,\delta )\).
-
Clearly,  Moreover,
Moreover,  This is because the modified normal mode of the simulator corresponds to answering \({\textsf {A}}\)’s commands exactly as in the real experiment. Hence, the theorem follows by the lemma below.
This is because the modified normal mode of the simulator corresponds to answering \({\textsf {A}}\)’s commands exactly as in the real experiment. Hence, the theorem follows by the lemma below.
Lemma 7

Proof
Fix \(i\in [q]\). By contradiction, assume that there exists a PPT attacker \({\textsf {A}}\), and some state \(\sigma \in \{0,1\}^{k}\), such that the following holds for the above defined simulator \(\textsf {S}\):
We build a PPT attacker \({\textsf {A}}'\) breaking continuous non-malleability of the code \(\Gamma \). A description of \({\textsf {A}}'\) follows:
\(\underline{\hbox {Attacker }{\textsf {A}}'\hbox { for }(\textsf {Init},\textsf {Enc},\textsf {Dec}):}\)
- 1.
Upon receiving the CRS \(\omega \), set \((\gamma ,\delta ) = (1,0)\), and pass \({\hat{\omega }}:= (\omega ,\gamma ,\delta )\) to \({\textsf {A}}\).
- 2.
For each round \(j \le i-1\), reply to \({\textsf {A}}\)’s commands as described in the ideal experiment. Let \(\sigma := \sigma ^{(i)}\) and \({{\hat{\omega }}} = (\omega ,i,\delta )\) be, respectively, the current stateFootnote 21 of the functionality and the CRS at the end of the \((i-1)\)-th round.
- 3.
Forward \((m_0 := \sigma ^{(i)}||i,m_1 := 0^k||0^{\log {\lambda }})\) to the challenger, and initialize \(\tilde{\sigma }||\tilde{\gamma }:= \varepsilon \) and \(\mathtt {mode}\) to \(\mathtt {normal}\). In case the simulation of the first \(i-1\) tampering queries has already caused the simulator to enter the overwritten mode, output a random \(b'\) and terminate; else, continue.
- 4.
For each round \(j \ge i\), upon input a command \(\langle \texttt {Tamper}, (f_{0}^{(j)}, f_{1}^{(j)})\rangle \) from \({\textsf {A}}\), query the tampering oracle \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),\cdot )\) with the pair of functions \(({\hat{f}_{0}}^{(j)},{\hat{f}_{1}}^{(j)})\) of Eq. (2). Then:
If the oracle returns \(\bot \), update the CRS to \({{\hat{\omega }}} := (\omega ,\gamma ,1)\).
If the oracle returns \(\diamond \), do nothing.
If the oracle returns a codeword \(\tilde{c}^{(j)} := (\tilde{c}_0^{(j)},\tilde{c}_1^{(j)})\), set \(\mathtt {mode}\) to \(\mathtt {overwritten}\) and overwrite \(\tilde{\sigma }||\tilde{\gamma }:= \textsf {Dec}(\omega ,(\tilde{c}_0^{(j)},\tilde{c}_1^{(j)}))\). If \(\tilde{\gamma }\ne \gamma \), update the CRS to \({{\hat{\omega }}} := (\omega ,\gamma ,1)\).
- 5.
For each round \(j \ge i\), upon input a command \(\langle \texttt {Leak},(g_{0}^{(j)}, g_{1}^{(j)})\rangle \) from \({\textsf {A}}\), query oracle \({\mathcal {O}}_\textsf {leak}^\ell (c_0,\cdot )\) and \({\mathcal {O}}_\textsf {leak}^\ell (c_1,\cdot )\) with the functions \({\hat{g}_{0}}^{(j)}\) and \({\hat{g}_{1}}^{(j)}\) of Eq. (3). Then, forward the answer \((\Lambda _0^{(j)},\Lambda _1^{(j)})\) to \({\textsf {A}}\).
- 6.
For each round \(j \ge i\), upon input a command \(\langle \texttt {Eval},x^{(j)}\rangle \) from \({\textsf {A}}\), if \(\delta =1\) return \(\bot \) to \({\textsf {A}}\). Else, proceed as follows:
If \(\mathtt {mode} = \mathtt {normal}\), let
and return \(y^{(j)}\) to \({\textsf {A}}\).
If \(\mathtt {mode} = \mathtt {overwritten}\), let
and return \(y^{(j)}\) to \({\textsf {A}}\).
Update the CRS to \({{\hat{\omega }}} = (\omega ,\gamma +1,\delta )\), and re-define \(\sigma := \sigma '\).
- 7.
Upon receiving a guess \(b'\) from \({\textsf {A}}\), output \(b'\) and terminate.
For the analysis, first note that \({\textsf {A}}'\) runs in polynomial time. Next, we claim that the simulation done by \({\textsf {A}}'\) is perfect. This is because:
-
The CRS \({\hat{\omega }}\) is distributed identically to the CRS in \(\mathbf{Hyb} _{\textsf {F},{\textsf {A}},\textsf {S}}^{(i-1)}(\lambda ,\sigma )\) and \(\mathbf{Hyb} _{\textsf {F},{\textsf {A}},\textsf {S}}^{(i)}(\lambda ,\sigma )\).
-
The first \(i-1\) leakage/tampering/execute queries are answered as in the ideal experiment, which corresponds to the way such queries are answered in both \(\mathbf{Hyb} _{\textsf {F},{\textsf {A}},\textsf {S}}^{(i-1)}(\lambda ,\sigma )\) and \(\mathbf{Hyb} _{\textsf {F},{\textsf {A}},\textsf {S}}^{(i-1)}(\lambda ,\sigma )\).
-
Let \(\mathbf{W} \) be the event that the simulation has already entered the overwritten mode while answering the first \(i-1\) tampering queries. Note that conditioning on \(\mathbf{W} \), the random variables \(\mathbf{Hyb} _{\textsf {F},{\textsf {A}},\textsf {S}}^{(i-1)}(\lambda ,\sigma )\) and \(\mathbf{Hyb} _{\textsf {F},{\textsf {A}},\textsf {S}}^{(i)}(\lambda ,\sigma )\) are identical, and thus Eq. (4) implies that \({\mathbb {P}}\left[ \lnot \mathbf{W} \right] \ge 1/\texttt {poly}(\lambda )\).
-
For each round \(j\ge i\), conditioning on \(\lnot \mathbf{W} \) and depending on the target encoding \((c_0,c_1)\) being either an encoding of \(\sigma ^{(i)}||i\) or an encoding of \(0^k||0^{\log {\lambda }}\), the queries of \({\textsf {A}}\) are answered exactly as in \(\mathbf{Hyb} _{\textsf {F},{\textsf {A}},\textsf {S}}^{(i-1)}(\lambda ,\sigma )\) or in \(\mathbf{Hyb} _{\textsf {F},{\textsf {A}},\textsf {S}}^{(i)}(\lambda ,\sigma )\). More precisely:
-
The remaining leakage and tampering queries are handled using the oracle \({\mathcal {O}}_\mathsf{maul}((c_0,c_1),\cdot )\). As in the proof of Theorem 4, the reduction needs to adjust the leakage/tampering functions taking into account the initial padding of the memory and the previous tampering queries. This can be done using Eq. (2) and Eq. (3) as before.
-
The remaining evaluation queries are perfectly emulated. Indeed, whenever \(\mathtt {mode}\) equals \(\mathtt {normal}\), the reduction answers evaluation queries by running \(\textsf {F}\) on the current state \(\sigma \) (this corresponds to the normal mode of simulator \(\textsf {S}\)). Similarly, whenever \(\mathtt {mode}\) equals \(\mathtt {overwritten}\), the reduction answers evaluation queries by running \(\textsf {F}\) on the current tampered state \(\tilde{\sigma }\) which results from applying the tampering functions to the initial memory (this corresponds to the overwritten mode of simulator \(\textsf {S}\)).
-
It follows that in case \((c_0,c_1)\) is an encoding of \(\sigma ^{(i)}||i\) and conditioning on \(\lnot \mathbf{W} \), the reduction perfectly emulates the view of \({\textsf {A}}\) in \(\mathbf{Hyb} _{\textsf {F},{\textsf {A}},\textsf {S}}^{(i-1)}(\lambda ,\sigma )\). Similarly, when \((c_0,c_1)\) is an encoding of \(0^k||0^{\log \lambda }\) and conditioning on \(\lnot \mathbf{W} \), the reduction perfectly emulates the view of \({\textsf {A}}\) in \(\mathbf{Hyb} _{\textsf {F},{\textsf {A}},\textsf {S}}^{(i)}(\lambda ,\sigma )\). Finally, \({\mathbb {P}}\left[ \lnot \mathbf{W} \right] \ge 1/\texttt {poly}(\lambda )\), and additionally conditioning on \(\mathbf{W} \) we have that \({\mathbb {P}}\left[ b'=b\right] = 1/2\). Hence, we have obtained:
a contradiction. This concludes the proof. \(\square \)
Notes
Our actual definition is stronger, in that as long as the tampered codeword \(\tilde{c}\) is valid, and \(\tilde{c}\ne c\), the adversary is even given \(\tilde{c}\) (and not just the corresponding decoded message). See Sect. 3 for a discussion.
For example, hard-wire \({\hat{c}_{1}}\), decode \(({\hat{c}_{0}},{\hat{c}_{1}})\), and overwrite \({\hat{c}_{0}}\) with garbage if the first bit of \({{\hat{m}}}\) is zero (otherwise leave it unchanged).
Of course, a similar guarantee must hold if we fix the right part \(c_1\) of the encoding.
Note that a counter only requires a logarithmic (in the security parameter) number of bits.
A similar statement holds for computationally secure LRS.
If not, \({\textsf {A}}_1\) obtains \(\diamond \) as answer to one of its tampering queries, and thus it can safely conclude that \({\hat{c}_{0}} = c_0\) and \({\hat{c}_{1}} \in \{c_1,c_1'\}\). Once \({\hat{c}_{0}}\) is known it is trivial to break non-malleability using an additional tampering query.
Namely, just have \(c_0\) (resp. \(c_1\)) contain \(\textit{pk}\), the encryption \(\gamma \) (resp. \(\gamma '\)) of any message \(m\) (resp. \(m' \ne m\)) under \(\textit{pk}\), and the corresponding argument \(\pi \) (resp. \(\pi '\)).
Note that this applies in particular to the encoding of [84].
To be more precise, this also requires to leak the initial hash values, to simulate the non-interactive arguments as done in the last hybrid, and to hard-wire those values in each leakage query.
This makes the reduction non-black-box, as it needs to run \({\textsf {A}}^*\) inside the leakage oracles.
Recall that the underlying LRS satisfies augmented leakage resilience (cf. Definition 5).
A family of hash functions \(\Psi = \{\psi _t: \{0,1\}^{2n} \rightarrow \{0,1\}^\lambda \}_{t\in \{0,1\}^\lambda }\) is weakly universal if for all distinct \(x_1, x_2 \in \{0,1\}^{2n}\) the following holds:
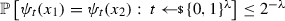 . Such families exist unconditionally.
. Such families exist unconditionally.Given an attacker \({\textsf {A}}^*\) that with non-negligible probability outputs a tampering query \((f_0^{(i)},f_1^{(i)})\) such that \((\tilde{c}_0^{(i)},\tilde{c}_1^{(i)})\) is valid with \(\tilde{h}_0^{(i)} = h_0\) and \(\tilde{s}_0^{(i)} \ne s_0\), we can build an attacker \({\textsf {A}}\) breaking collision resistance of \((\textsf {Gen},\textsf {Hash})\). The reduction is straightforward: Given \(\textit{hk}\), adversary \({\textsf {A}}\) simply runs \({\textsf {A}}^*\) honestly after embedding \(\textit{hk}\) in the CRS, until it outputs the query \((f_0^{(i)},f_1^{(i)})\), which yields the collision \((s_0,\tilde{s}_0^{(i)})\).
The reduction is analogous to the one in Lemma 4, and therefore omitted.
The reduction is analogous to the one in Footnote 14.
Attacker \({\textsf {A}}\) simply runs \({\textsf {A}}^*\) on a simulated codeword \((c_0,c_1)\) generated exactly as in the last hybrid, and answers to both leakage and tampering queries honestly until \({\textsf {A}}^*\) outputs the query \((f_0^{(i)},f_1^{(i)})\) breaking uniqueness.
We stress that weak non-malleability actually suffices for this application. We use super non-malleability for simplicity (and to be consistent with the rest of the paper).
After such a query, the functionality internally re-defines \(\sigma := \sigma '\).
Note that the reduction can compute \(\sigma ^{(i)}\), as it receives the initial state \(\sigma \) as auxiliary input.
References
D. Aggarwal, Affine-evasive sets modulo a prime. Inf. Process. Lett. 115(2), 382–385 (2015).
D. Aggarwal, S. Agrawal, D. Gupta, H. K. Maji, O. Pandey, M. Prabhakaran, Optimal computational split-state non-malleable codes, in TCC (2016), pp. 393–417.
D. Aggarwal, Y. Dodis, T. Kazana, M. Obremski, Non-malleable reductions and applications, in STOC (2015), pp. 459–468.
D. Aggarwal, Y. Dodis, S. Lovett, Non-malleable codes from additive combinatorics, in STOC (2014), pp. 774–783.
D. Aggarwal, Y. Dodis, S. Lovett, Non-malleable codes from additive combinatorics. SIAM J. Comput. 47(2), 524–546 (2018).
D. Aggarwal, N. Döttling, J, B. Nielsen, M. Obremski, E. Purwanto, Continuous non-malleable codes in the 8-split-state model, in EUROCRYPT (2019), pp. 531–561.
D. Aggarwal, S. Dziembowski, T. Kazana, M. Obremski, Leakage-resilient non-malleable codes, in TCC (2015), pp. 398–426.
D. Aggarwal, T. Kazana, M. Obremski, Inception makes non-malleable codes stronger, in TCC (2017), pp. 319–343.
S. Agrawal, D. Gupta, H. K. Maji, O. Pandey, M. Prabhakaran, Explicit non-malleable codes against bit-wise tampering and permutations, in CRYPTO (2015), pp. 538–557.
S. Agrawal, D. Gupta, H. K. Maji, O. Pandey, M. Prabhakaran, A rate-optimizing compiler for non-malleable codes against bit-wise tampering and permutations, in TCC (2015), pp. 375–397.
P. Austrin, K.-M. Chung, M. Mahmoody, R. Pass, K. Seth, On the impossibility of cryptography with tamperable randomness, in CRYPTO (2014), pp. 462–479.
M. Ball, D. Dachman-Soled, S. Guo, T. Malkin, L.-Y. Tan, Non-malleable codes for small-depth circuits, in FOCS (2018), pp. 826–837.
M. Ball, D. Dachman-Soled, M. Kulkarni, H. Lin, T. Malkin, Non-malleable codes against bounded polynomial time tampering, in EUROCRYPT (2019), pp. 501–530.
M. Ball, D. Dachman-Soled, M. Kulkarni, T. Malkin, Non-malleable codes for bounded depth, bounded fan-in circuits, in EUROCRYPT (2016), pp. 881–908.
M. Ball, D. Dachman-Soled, M. Kulkarni, T. Malkin. Non-malleable codes from average-case hardness: \({{\sf AC}}^{0}\), decision trees, and streaming space-bounded tampering, in EUROCRYPT (2018), pp. 618–650.
M. Ball, D. Dachman-Soled, M. Kulkarni, T. Malkin, Limits to non-malleability, in ITCS (2020), pp. 80:1–80:32.
M. Ball, S. Guo, D. Wichs, Non-malleable codes for decision trees, in CRYPTO (2019), pp. 413–434.
M. Bellare, D. Cash, R. Miller, Cryptography secure against related-key attacks and tampering, in ASIACRYPT (2011), pp. 486–503.
M. Bellare, M. Fischlin, S. Goldwasser, S. Micali, Identification protocols secure against reset attacks, in EUROCRYPT (2001), pp. 495–511.
M. Bellare, T. Kohno, A theoretical treatment of related-key attacks: RKA-PRPs, RKA-PRFs, and applications, in EUROCRYPT (2003), pp. 491–506.
M. Bellare, K. G. Paterson, S. Thomson, RKA security beyond the linear barrier: IBE, encryption and signatures, in ASIACRYPT (2012), pp. 331–348.
D. Boneh, R. A. DeMillo, R. J, Lipton. On the importance of eliminating errors in cryptographic computations, J. Cryptol. 14(2), 101–119 (2001).
G. Brian, A. Faonio, D. Venturi, Continuously non-malleable secret sharing for general access structures, in TCC (2019), pp. 211–232.
N. Chandran, V. Goyal, P. Mukherjee, O. Pandey, J. Upadhyay, Block-wise non-malleable codes, in ICALP (2016), pp. 31:1–31:14.
N. Chandran, B. Kanukurthi, S. Raghuraman Information-theoretic local non-malleable codes and their applications, in TCC (2016), pp. 367–392.
E. Chattopadhyay, V. Goyal, X. Li, Non-malleable extractors and codes, with their many tampered extensions, in STOC (2016), pp. 285–298.
E. Chattopadhyay, X. Li, Non-malleable codes and extractors for small-depth circuits, and affine functions, in STOC (2017), pp. 1171–1184.
E. Chattopadhyay, D. Zuckerman, Non-malleable codes against constant split-state tampering, in FOCS (2014), pp. 306–315.
B. Chen, Y. Chen, K. Hostáková, P. Mukherjee, Continuous space-bounded non-malleable codes from stronger proofs-of-space, in CRYPTO (2019), pp. 467–495.
M. Cheraghchi, V. Guruswami, Non-malleable coding against bit-wise and split-state tampering, in TCC (2014), pp. 440–464.
M. Cheraghchi, V. Guruswami, Capacity of non-malleable codes. IEEE Trans. Inf. Theory, 62(3), 1097–1118 (2016).
M. Cheraghchi, V. Guruswami, Non-malleable coding against bit-wise and split-state tampering, J. Cryptol. 30(1), 191–241 (2017).
S. G. Choi, A. Kiayias, T. Malkin, BiTR: Built-in tamper resilience, in ASIACRYPT (2011), pp. 740–758.
S. Coretti, Y. Dodis, B. Tackmann, D. Venturi. Non-malleable encryption: simpler, shorter, stronger, in TCC (2016), pp. 306–335.
S. Coretti, A. Faonio, D. Venturi, Rate-optimizing compilers for continuously non-malleable codes, in ACNS (2019), pp. 3–23.
S. Coretti, U. Maurer, B. Tackmann, D. Venturi, From single-bit to multi-bit public-key encryption via non-malleable codes, in TCC (2015), pp. 532–560.
R. Cramer, I. Damgård, N. Döttling, I. Giacomelli, C. Xing, Linear-time non-malleable codes in the bit-wise independent tampering model, in ICITS (2017), pp. 1–25.
R. Cramer, V. Shoup, A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack, in CRYPTO (1998), pp. 13–25.
D. Dachman-Soled, Y. T. Kalai, Securing circuits against constant-rate tampering, in CRYPTO (2012), pp. 533–551.
D. Dachman-Soled, Y. T. Kalai, Securing circuits and protocols against 1/poly(k) tampering rate, in TCC (2014), pp. 540–565.
D. Dachman-Soled, M. Kulkarni, Upper and lower bounds for continuous non-malleable codes, in PKC (2019), pp. 519–548.
D. Dachman-Soled, M. Kulkarni, A. Shahverdi, Tight upper and lower bounds for leakage-resilient, locally decodable and updatable non-malleable codes, in PKC (2017), pp. 310–332.
D. Dachman-Soled, M. Kulkarni, A. Shahverdi, Local non-malleable codes in the bounded retrieval model, in PKC (2018), pp. 281–311.
D. Dachman-Soled, M. Kulkarni, A. Shahverdi, Tight upper and lower bounds for leakage-resilient, locally decodable and updatable non-malleable codes, Inf. Comput. p. 268 (2019)
D. Dachman-Soled, F.-H. Liu, E. Shi, H.-S. Zhou, Locally decodable and updatable non-malleable codes and their applications, in TCC (2015), pp. 427–450.
D. Dachman-Soled, F.-H. Liu, E. Shi, H.-S. Zhou, Locally decodable and updatable non-malleable codes and their applications. J. Cryptol. 33(1), 319–355 (2020).
I. Damgård, S. Faust, P. Mukherjee, D. Venturi, Bounded tamper resilience: How to go beyond the algebraic barrier, in ASIACRYPT (2013), pp. 140–160.
I. Damgård, S. Faust, P. Mukherjee, D. Venturi, The chaining lemma and its application, in ICITS (2015), pp. 181–196.
I. Damgård, T. Kazana, M. Obremski, V. Raj, L. Siniscalchi, Continuous NMC secure against permutations and overwrites, with applications to CCA secure commitments, in TCC (2018), pp. 225–254.
F. Davì, S. Dziembowski, D. Venturi, Leakage-resilient storage, in SCN (2010), pp. 121–137.
Y. Dodis, K. Haralambiev, A. López-Alt, D. Wichs, Efficient public-key cryptography in the presence of key leakage, in ASIACRYPT (2010), pp. 613–631.
S. Dziembowski, S. Faust, Leakage-resilient cryptography from the inner-product extractor, in ASIACRYPT (2011), pp. 702–721.
S. Dziembowski, T. Kazana, M. Obremski, Non-malleable codes from two-source extractors, in CRYPTO (2013), pp. 239–257.
S. Dziembowski, K. Pietrzak, Leakage-resilient cryptography. In FOCS (2008), pp. 293–302.
S. Dziembowski, K. Pietrzak, D. Wichs, Non-malleable codes, in ICS (2010), pp. 434–452.
S. Dziembowski, K. Pietrzak, D. Wichs, Non-malleable codes. J. ACM, 65(4), 20:1–20:32 (2018).
A. Faonio, J. B. Nielsen, Non-malleable codes with split-state refresh, in PKC (2017), pp. 279–309.
A. Faonio, J. B. Nielsen, M. Simkin, D. Venturi, Continuously non-malleable codes with split-state refresh, in ACNS (2018), pp. 121–139.
A. Faonio, J. B. Nielsen, M. Simkin, D. Venturi, Continuously non-malleable codes with split-state refresh. Theor. Comput. Sci. 759, 98–132 (2019).
A. Faonio, D. Venturi, Non-malleable secret sharing in the computational setting: adaptive tampering, noisy-leakage resilience, and improved rate, in CRYPTO (2019), pp. 448–479.
S. Faust, K. Hostáková, P. Mukherjee, D. Venturi, Non-malleable codes for space-bounded tampering, in CRYPTO (2017), pp. 95–126.
S. Faust, P. Mukherjee, J. B. Nielsen, D. Venturi, Continuous non-malleable codes, in TCC (2014), pp. 465–488.
S. Faust, P. Mukherjee, J. B. Nielsen, D. Venturi, A tamper and leakage resilient von Neumann architecture, in PKC (2015), pp. 579–603.
S. Faust, P. Mukherjee, D. Venturi, D. Wichs, Efficient non-malleable codes and key-derivation for poly-size tampering circuits, in EUROCRYPT (2014), pp. 111–128.
S. Faust, P. Mukherjee, D. Venturi, D. Wichs, Efficient non-malleable codes and key derivation for poly-size tampering circuits. IEEE Trans. Inf. Theory 62(12), 7179–7194 (2016).
S. Faust, K. Pietrzak, D. Venturi, Tamper-proof circuits: How to trade leakage for tamper-resilience, in ICALP (2011), pp. 391–402.
S. Fehr, P. Karpman, B. Mennink, Short non-malleable codes from related-key secure block ciphers. IACR Trans. Symmetr. Cryptol. 2018(1), 336–352 (2018).
U. Feige, D. Lapidot, A. Shamir, Multiple non-interactive zero knowledge proofs based on a single random string (extended abstract), in FOCS (1990), pp. 308–317.
D. Genkin, Y. Ishai, M. Prabhakaran, A. Sahai, E. Tromer, Circuits resilient to additive attacks with applications to secure computation, in STOC (2014), pp. 495–504.
R. Gennaro, A. Lysyanskaya, T. Malkin, S. Micali, T. Rabin, Algorithmic tamper-proof (ATP) security: theoretical foundations for security against hardware tampering, in TCC (2004), pp. 258–277.
V. Goyal, A. Kumar, Non-malleable secret sharing, in STOC (2018), pp. 685–698.
V. Goyal, A. Sahai, Resettably secure computation, in EUROCRYPT (2009), pp. 54–71.
J. Groth, Simulation-sound NIZK proofs for a practical language and constant size group signatures, in ASIACRYPT (2006), pp. 444–459.
J. Groth, A. Sahai, Efficient non-interactive proof systems for bilinear groups, in EUROCRYPT (2008), pp. 415–432.
Jens Groth and Amit Sahai. Efficient noninteractive proof systems for bilinear groups. SIAM J. Comput., 41(5):1193–1232, 2012.
Y. Ishai, M. Prabhakaran, A. Sahai, D. Wagner, Private circuits II: Keeping secrets in tamperable circuits, in EUROCRYPT (2006), pp. 308–327.
Z. Jafargholi, D. Wichs, Tamper detection and continuous non-malleable codes, in TCC (2015), pp. 451–480.
Y. T. Kalai, B. Kanukurthi, A. Sahai, Cryptography with tamperable and leaky memory, in CRYPTO (2015), pp. 373–390.
B. Kanukurthi, S. L. B. Obbattu, S. Sekar, Four-state non-malleable codes with explicit constant rate, in TCC (2017), pp. 344–375.
B. Kanukurthi, S. L. B. Obbattu, S. Sekar, Four-state non-malleable codes with explicit constant rate. J. Cryptol. 33(3), 1044–1079 (2020).
A. Kiayias, F.-H. Liu, Y. Tselekounis, Practical non-malleable codes from \(l\)-more extractable hash functions, in CCS (2016), pp. 1317–1328.
A. Kiayias, F.-H. Liu, Y. Tselekounis, Non-malleable codes for partial functions with manipulation detection, in CRYPTO (2018), pp. 577–607.
A. Kiayias, Y. Tselekounis, Tamper resilient circuits: The adversary at the gates, in ASIACRYPT (2013), pp. 161–180.
F.-H. Liu, A. Lysyanskaya, Tamper and leakage resilience in the split-state model, in CRYPTO (2012), pp. 517–532.
R. Ostrovsky, G. Persiano, D. Venturi, I. Visconti. Continuously non-malleable codes in the split-state model from minimal assumptions, in CRYPTO (2018), pp. 608–639.
K. Pietrzak, Subspace LWE, in TCC (2012), pp. 548–563.
A. D. Santis, G. Di Crescenzo, R. Ostrovsky, G. Persiano, A. Sahai, Robust non-interactive zero knowledge, in CRYPTO (2001), pp. 566–598.
S. Yilek, Resettable public-key encryption: How to encrypt on a virtual machine, in CT-RSA (2010), pp. 41–56.
Acknowledgements
Open access funding provided by Università degli Studi di Roma La Sapienza within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jonathan Katz.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Faust, S., Mukherjee, P., Nielsen, J.B. et al. Continuously Non-malleable Codes in the Split-State Model. J Cryptol 33, 2034–2077 (2020). https://doi.org/10.1007/s00145-020-09362-z
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00145-020-09362-z





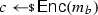 using the encoding procedure.
using the encoding procedure.


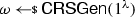 and
and 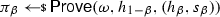 are replaced by
are replaced by 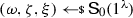 and
and 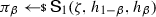 respectively.
respectively.
 and
and  ; set
; set  , and run
, and run  .
. .
. .
. ), and thus, by the union bound, the simulation is wrong with probability at most
), and thus, by the union bound, the simulation is wrong with probability at most  and let
and let  , and let
, and let  .
. where
where  and let
and let  , and let
, and let  .
. .
. , and then start
, and then start  : Sample
: Sample 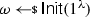 , initialize
, initialize 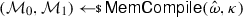 : Let
: Let  . Parse
. Parse  : Parse
: Parse  . Finally, update the CRS to
. Finally, update the CRS to 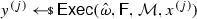 : If
: If 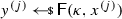 and reply with
and reply with 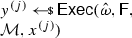 and reply with
and reply with  and return
and return  and return
and return  : Sample
: Sample 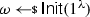 , initialize
, initialize  : Parse
: Parse 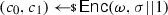 . For
. For 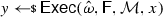 : Parse
: Parse 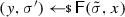 , run
, run 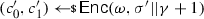 , and for each
, and for each 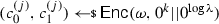 , and let
, and let 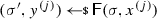 , where
, where 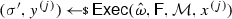 and reply with
and reply with 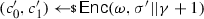 , and update the first n bits of
, and update the first n bits of  is run, and
is run, and  , and let
, and let  where
where  and return
and return  and return
and return 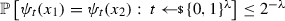 . Such families exist unconditionally.
. Such families exist unconditionally.