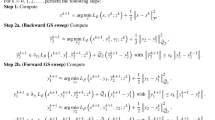Finite Element Numerical Approximation for Two Image Denoising Models

Abstract

Finite difference method (FDM) is a well-established variational computational technique to solve problems in image analysis. Compared to the extensively discussed finite difference schemes, very few work has been devoted to finite element method (FEM), which motivates the proposed work. On one hand, FEM has strong physical backgrounds, which allows clear and physically meaningful derivation of difference equations that are easy to implement. On the other hand, combined with the variational methods, the semidiscrete FEM scheme in timescale can give favorable stability and efficiency properties of computations. In this paper, we firstly introduce two classical image denoising models, the Perona–Malik (P–M) model and You–Kaveh (Y–K) model. Then, the finite element numerical algorithm is given for the two models, and the numerical analysis of the algorithm is also presented. These two models correspond to two kinds of nonlinear partial differential equations, the former of which is of fourth order and the latter is of second order. Compared results demonstrate the superiority of the proposed FEM over FDM, in terms of suppressing blocky effects while maintaining the visual quality.

Appendix

The finite difference numerical approximation is considered as follows [13]

The discrete grid point is defined as $(ih,jh,n\triangle t)$, and $u^{k}_{i,j}$ is defined to approximate u(x, y, t) with $x=ih,~y=jh,~t=n\triangle t~(i,j=1,2,3,\ldots ,N)$, $g_{i,j}=g(|\nabla u_\sigma |)_{i,j}$. Denote a time step size $\triangle t$ and a space grid size $\triangle x =\triangle y =h=1$. Finally, the numerical approximation to (1.2) is given as

$$\begin{aligned} \frac{u^{k+1}_{i,j}-u^{k}_{i,j}}{\triangle t}= & {} \frac{g^k_{i-1,j}+g^k_{i,j}}{2}(u^{k+1}_{i-1,j}-u^{k+1}_{i,j}) \\&+\frac{g^k_{i+1,j}+g^k_{i,j}}{2}(u^{k+1}_{i+1,j}-u^{k+1}_{i,j}) \\&+\frac{g^k_{i,j-1}+g^k_{i,j}}{2}(u^{k+1}_{i,j-1}-u^{k+1}_{i,j}) \\&+\frac{g^k_{i,j+1}+g^k_{i,j}}{2}(u^{k+1}_{i,j+1}-u^{k+1}_{i,j}). \end{aligned}$$

P–M equation (1.2) is associated with the following energy functional

$$\begin{aligned} E(u)=\int _{\Omega }f(|\nabla u|)\mathrm{d}x\mathrm{d}y. \end{aligned}$$

$f(\cdot )\ge 0$ is an increasing function associated with the diffusion coefficient as

$$\begin{aligned} g(s)=f'(s)/s. \end{aligned}$$

The differential equation (1.3) may be solved numerically using finite difference approach. Assuming a time step size of $\triangle t$ and a space grid size of h, we quantize the time and space coordinates as follows:

$$\begin{aligned} t= & {} n\triangle t,\quad n=1,2,\ldots \\ x= & {} ih,\quad i=1,2,\ldots ,N \\ t= & {} jh,\quad j=1,2,\ldots ,N \end{aligned}$$

where $N\times N$ is the size of image support. We calculate the Laplacian of the image intensity function as

$$\begin{aligned} \nabla ^2 u^n_{i,j}=\frac{u^n_{i+1,j}+u^n_{i-1,j}+u^n_{i,j+1}+u^n_{i,j-1}-4u^n_{i,j}}{h^2} \end{aligned}$$

and

$$\begin{aligned} c(\nabla ^2 u)=g(|\nabla ^2 u|)\nabla ^2 u. \end{aligned}$$

Denote

$$\begin{aligned} c^n_{i,j}=c(\nabla ^2 u^n_{i,j}). \end{aligned}$$

At the end stage, we calculate the Laplacian of $c(\cdot )$ as

$$\begin{aligned} \nabla ^2 c^n_{i,j}=\frac{c^n_{i+1,j}+c^n_{i-1,j}+c^n_{i,j+1}+c^n_{i,j-1}-4c^n_{i,j}}{h^2}. \end{aligned}$$

Finally, the numerical approximation to the differential equation (1.3) is given as

$$\begin{aligned} u^{n+1}_{i,j}=u^n_{i,j}-\triangle t\nabla ^2 c^n_{i,j}. \end{aligned}$$

The finite difference numerical scheme of Y–K model is analogous to P–M model.

Moreover, in order to assess the performance of proposed diffusion models, different quantitative measures are calculated using ground truth image (u) and noisy image (f), and the noise is $n=f-u$. For quantitative evaluation, a widely used measure, signal-to-noise ratio (SNR) can be given as

$$\begin{aligned} \mathrm{SNR}=10\log _{10}{\frac{\sum _{i=1}^M \sum _{j=1}^N (u_{ij})^2}{\sum _{i=1}^M \sum _{j=1}^N (u_{ij}-f_{ij})^2}}. \end{aligned}$$

In addition to SNR, mean-square error (MSE) is defined as

$$\begin{aligned} \mathrm{MSE}=\frac{1}{MN} \sum _{i=1}^M \sum _{j=1}^N (f_{ij}-u_{ij})^2. \end{aligned}$$

where M and N are numbers of rows and columns, respectively.

We also adopt the structure similarity (SSIM) index to find the similarity between the luminance, contrast and structure of two different images

$$\begin{aligned} \mathrm{SSIM}(X,Y)=\frac{(2\mu _x \mu _y+c_1)(2\sigma _{xy}+c_2)}{(\mu _x ^2 +\mu _y ^2+c_1)(\sigma _x ^2+\sigma _y ^2+c_2)}, \end{aligned}$$

where $\mu _x$ and $\mu _y$ are the mean intensities of X and Y and $\sigma _x$ and $\sigma _y$ are the standard deviations of X and Y. The constants are used to avoid instability.

The peak signal-to-noise ratio can be defined as

$$\begin{aligned} \mathrm{PSNR}=10\log _{10}{\frac{MN|\mathrm{max}(u)-\mathrm{min}(u)|^2}{\parallel f-u \parallel ^2_{L^2}}}. \end{aligned}$$

The peak signal-to-noise ratio can be defined as

$$\begin{aligned} \mathrm{RMSE}=\sqrt{\frac{\sum _{i=1}^n (X_{\mathrm{obs},i}-X_{\mathrm{model},i})^2}{n}}. \end{aligned}$$