Skip to main content
SpringerLink
Log in

Decomposition of Third-Order Linear Time-Varying Systems into Its Second- and First-Order Commutative Pairs

  • Published:
Circuits, Systems, and Signal Processing Aims and scope Submit manuscript

Abstract

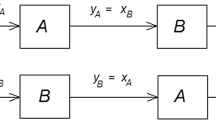
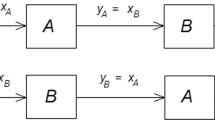
Decomposition is a common tool for the synthesis of many physical systems. It is also used for analyzing large-scale systems which are then known as tearing and reconstruction. On the other hand, commutativity of cascade-connected systems has gained a great deal of interest, and its possible benefits have been pointed out on the literature. In this paper, the necessary and sufficient conditions for decomposition of any third-order linear time-varying system as a commutative pair of first- and second-order systems of which parameters are also explicitly expressed, are investigated. Further, additional requirements in case of nonzero initial conditions are derived. This paper highlights the direct formulas for realization of any third-order linear time-varying systems as a series (cascade) connection of first- and second-order subsystems. This series connection is commutative so that it is independent from the sequence of subsystems in the connection. Hence, the convenient sequence can be decided by considering the overall performance of the system when the sensitivity, disturbance, and robustness effects are considered. Realization covers transient responses as well as steady-state responses.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. M. Arnoldy, N. Begunz, P. Gurevichx, E. Kwamey, H. Lamba, D. Rachinskii, Dynamics of discrete time systems with a hysteresis stop operator. SIAM J. Appl. Dyn. Syst. 16, 91–119 (2017)

    Article  MathSciNet  Google Scholar 

  2. W.N. Dale, M.C. Smith, Stabilizability and existence of system representations for discrete-time time-varying systems. SIAM J. Control Optim. 31, 1538–1557 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  3. I. Dassios, Optimal solutions for non-consistent singular linear systems of fractional nabla difference equations. Circ. Syst. Signal Process. 34, 1769–1797 (2015)

    Article  MATH  Google Scholar 

  4. I. Dassios, D. Baleanu, G. Kalogeropoulos, On non-homogeneous singular systems of fractional nabla difference equations. Appl. Math. Comput. 227, 112–131 (2014)

    MathSciNet  MATH  Google Scholar 

  5. I. Gohberg, M.A. Kaashoek, A.C.M. Ran, Partial role and zero displacement by cascade connection. SIAM J. Matrix Anal. Appl. 10, 316–325 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  6. C. Jaeger, T.N. Blalock, Microelectronic Circuit Design, 3rd edn. (McGraw-Hill, Boston, 2006)

    Google Scholar 

  7. M. Koksal, A Survey on the commutativity of time-varying systems, METU, Gaziantep Engineering Faculty, Technical Report no: GEEE CAS-85/1 (1985)

  8. M. Koksal, An exhaustive study on the commutativity of time-varying systems. Int. J. Control 47, 1521–1537 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  9. M. Koksal, Commutativity of second-order time-varying systems. Int. J. Control 36, 541–544 (1982)

    Article  MathSciNet  Google Scholar 

  10. M. Koksal, Corrections on ‘commutativity of second-order time-varying systems’. Int. J. Control 38, 273–274 (1983)

    Article  MathSciNet  Google Scholar 

  11. M. Koksal, General conditions for commutativity of time-varying systems, in Proceedings of the international conference on telecommunication and control, Halkidiki, Greece, pp. 223–225 (1984)

  12. M.E. Koksal, Decomposition of a second-order linear time-varying differential system as the series connection of two first-order commutative pairs. Open Math. 14, 693–704 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  13. M.E. Koksal, Inverse commutativity conditions for second-order linear time-varying systems. J. Math. 2017, 1–6 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  14. M. Koksal, M.E. Koksal, Commutativity of cascade connected discrete time linear time-varying systems (in Turkish), in 2013 automatic control national meeting TOK”2013, Malatya-Turkey, pp. 1128–1131 (2013)

  15. M. Koksal, M.E. Koksal, Commutativity of cascade connected discrete time linear time-varying systems. Trans. Inst. Meas. Control 37, 615–622 (2015)

    Article  Google Scholar 

  16. M. Koksal, M.E. Koksal, Commutativity of linear time-varying differential systems with non-zero initial conditions: a review and some new extensions. Math. Probl. Eng. 2011, 1–25 (2011)

    Article  MATH  Google Scholar 

  17. H.A. Levine, Y.J. Seo, Discrete dynamical systems in multiple target and alternate SELEX. SIAM J. Appl. Dyn. Syst. 14, 1048–1101 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  18. R.G. Lyons, Understanding Digital Signal Processing, 3rd edn. (Prentice Hall, Englewood Cliffs, 2011)

    Google Scholar 

  19. E. Marshal, Commutativity of time varying systems. Electron. Lett. 13, 539–540 (1977)

    Article  Google Scholar 

  20. H.N. Nguyen, S. Olaru, P.O. Gutman, M. Hovd, Constrained control of uncertain, time-varying linear discrete-time systems subject to bounded disturbances. IEEE Trans. Autom. Control 60, 831–836 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  21. K. Ninomiya, K. Harada, I. Miyazaki, Stability analysis of an active filter using cascade connection of switching regulators. Electron. Commun. Jpn. Part I Commun. 80, 87–94 (1997)

    Article  Google Scholar 

  22. A.V. Oppenheim, R.W. Schafer, Discrete-Time Signal Processing (Prentice-Hall, Engle-wood Cliffs, 1989), p. 406

    MATH  Google Scholar 

  23. B. Rahman, K.B. Blyuss, Y.N. Kyrychko, Dynamics of neural systems with discrete and distributed time delays. SIAM J. Appl. Dyn. Syst. 14, 2069–2095 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  24. S.V. Salehi, Comments on ‘commutativity of second-order time-varying systems’. Int. J. Control 37, 1195–1196 (1983)

    Article  MATH  Google Scholar 

  25. W.J. Shi, Y. Yao, T.Q. Zhang, X.J. Meng, A method of recognizing biology surface spectrum using cascade-connection artificial neural nets. Spectrosc. Spectr. Anal. 28, 983–987 (2008)

    Google Scholar 

  26. D. Vasileska, S.M. Goodnick, Computational Electronics (Morgan & Claypool Publishers, San Rafael, 2006)

    Google Scholar 

  27. F. Wirth, Dynamics of time-varying discrete-time linear systems: spectral theory and the protected system. SIAM J. Control Optim. 36, 447–487 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  28. J.M. Zhang, W.F. Qi, T. Tian, W.X. Wang, Further results on the decomposition of an NFSR into the cascade connection of an NFSR Into an LFSR. IEEE Trans. Inf. Theory 61, 645–654 (2015)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The first author was supported by the Scientific and Technological Research Council of Turkey under the Project 115E952.

Author information

Authors and Affiliations

  1. Department of Mathematics, Ondokuz Mayis University, 55139, Atakum, Samsun, Turkey

    Mehmet Emir Koksal

  2. Department of Mathematics, Gaziosmanpasa University, 60250, Tokat, Turkey

    Ali Yakar

Authors
  1. Mehmet Emir Koksal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ali Yakar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Mehmet Emir Koksal.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Koksal, M.E., Yakar, A. Decomposition of Third-Order Linear Time-Varying Systems into Its Second- and First-Order Commutative Pairs. Circuits Syst Signal Process 38, 4446–4464 (2019). https://doi.org/10.1007/s00034-019-01075-4

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00034-019-01075-4

Keywords

Search

Navigation