1 Introduction

In recent years, a great interest has been aroused by the analysis of electrical and electronic systems with fractional-order elements, especially with supercapacitors. Experimental studies show that both the frequency characteristics and transient states in such systems differ from the characteristics and waveforms occurring in classic, integer-order RLC circuits [1, 5]. For systems containing supercapacitors, these differences are mainly due to their electrochemical construction [8]. Besides supercapacitors, many new practical realizations of the fractional-order capacitor \({C}_{\alpha }\) have been developed, among others using the equivalent RC ladder structures, some dielectrics (e.g., \(\hbox {LiN}_2\hbox {H}_5\hbox {SO}_4\)), fractal systems [4, 14, 27] and many others. For the description of lossy coils with soft ferromagnetic cores, fractional-order models have been used too [28, 29]. There are also works on the fractional-order description of magnetically coupled coils [31] and memristors as well as circuits and systems with memristors [13, 17]. Fractional calculus has been applied for the description of phenomena in many scientific fields, not only technical. For example, in biological and medical sciences, it has been used to describe peristaltic movements of the intestines [32]. In a related area to the circuit theory—in signal processing, it has been used to design analog and digital fractional-order filters [6, 20, 24].

Studies on the systems and circuits with fractional-order elements \({L}_{\beta }, {C}_{\alpha }\) (including circuits with supercapacitors) are mainly conducted in three directions. The first one involves the study of the frequency properties and characteristics of circuits of the class \({RL}_{\beta }{C}_{\alpha }\) [21, 25, 26, 35, 36] and circuits of the class \({RLC}_{\alpha }\) with supercapacitors [9, 30, 33, 34], analysis of transient states in such systems [3, 7, 9, 10, 12] and analysis of their stability [11, 22].

The second one, experimental, concerns the measurements of frequency characteristics and steady-state as well as transient-state waveforms occurring in such systems and the identification of fractional-order parameters in both time and frequency domain [2, 5].

The third direction concerns theoretical and practical realizations of different fractional-order elements [6, 25] or systems, e.g., oscillators [23].

The paper belongs to the first mentioned direction of studies, and it concerns an analysis of transient states in series circuit of the class \({RL}_{\beta }{C}_{\alpha }\), supplied by a voltage source of any kind.

There are a few works concerning this issue [3, 7, 9, 10, 12]. The paper [9] presents an analysis of an electrical circuit of the class \({RC}_{\alpha }\), where the voltage excitation is a unit step function and it analyzes the delay, rise and settling times of the fractional-order circuit. Analysis of free oscillations in the series circuit of the class \({RL}_{\beta }{C}_{\alpha }\) has been performed in [7], and analytical solution for \({\alpha }\) = \({\beta }\) has been obtained. In the paper [3], an analysis of parallel \({RL}_{\beta }{C}_{\alpha }\) circuit has been performed with a unit step function as the voltage excitation. For the specific case, \({\alpha } = {\beta }\), an analytical solution has been found, but for the general case, \({\alpha } \ne {\beta }\), solutions have been found numerically. Generalized method of solving transient states in circuits of the class \({RL}_{\beta }{C}_{\alpha }\), by defining state equations of the concerned circuit, has been described in the work [12].

In contrast to previous works, this paper describes a method of analysis of transient states in a series circuit of the class \({RL}_{\beta }{C}_{\alpha }\) for any kind of the voltage excitation and arbitrary values of parameters \({\alpha }, {\beta }\in {\mathbb {R}^{+}}\), resulting in closed form solutions. The paper is a continuation of work [10] concerning analysis of the transient state in a series circuit of the class \({RC}_{\alpha }\) with the supercapacitor modeled as a fractional-order capacitor \({C}_{\alpha }\).

2 Formalization of the Problem

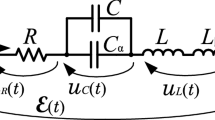
The model of the analyzed circuit of the class \({RL}_{\beta }{C}_{\alpha }\), with the supercapacitor and the fractional-order coil, is shown in Fig. 1. It consists of a series resistance \({R}_S\), an inductance \({L}_{\beta }\) and a supercapacitor of (pseudo)capacitance \({C}_{\alpha }\) with fractional orders \({\alpha }, {\beta }\in {\mathbb {R}^{+}}\). The analysis takes into account the series internal resistance \({R}_L\) of the real coil and of the supercapacitor (\({R}_C\)—ESR resistance). The circuit from Fig. 1 is supplied by a voltage source of an arbitrary waveform.

Fig. 1
figure 1

Model of the analyzed series \({RL}_{\beta }{C}_{\alpha }\) circuit

Full size image

In the transient-state analysis of the circuit from Fig. 1, the waveforms of the voltages \({u}_{C_{\alpha }}({t}), {u}_{C}({t})\) across the capacitor, the voltages \({u}_{L{\beta }}({t}), {u}_{L}({t})\) across the coil and the current i(t) have been calculated. Assuming zero initial conditions, i.e., \({u}_{C}(0) = 0, {i}_L(0) = 0\), and simple fractional-order models of the inductance \({L}_{\beta }\) and the capacitance \({C}_{\alpha }\):

$$\begin{aligned} u_{L{\beta }}\left( t \right) =L_{{\beta }}\frac{\mathrm {d}^{{\beta }}i\left( t \right) }{\mathrm {d} t^{{\beta }}}, \end{aligned}$$
(1)

and:

$$\begin{aligned} i\left( t \right) =C_{{\alpha }}\frac{\mathrm {d}^{{\alpha }}u_{C{\alpha }}\left( t \right) }{\mathrm {d} t^{{\alpha }}}, \end{aligned}$$
(2)

the voltage Kirchhoff’s law for the considered circuit results in:

$$\begin{aligned} e\left( t \right) -\left( R_{S}+R_{L}+R_{C} \right) i\left( t \right) -u_{L{\beta }}\left( t \right) -u_{C{\alpha }}\left( t \right) =0. \end{aligned}$$
(3)

Using formulae (1) and (2), this equation can be converted to a fractional-order differential equation of the voltage \({u}_{C{\alpha }}\)(t) function:

$$\begin{aligned} \frac{\mathrm {d}^{({\alpha }+{\beta })}u_{C{\alpha }}(t) }{\mathrm {d} t^{({\alpha }+{\beta })}}+\frac{R_{Z}}{L}\frac{\mathrm {d}^{\alpha }u_{C{\alpha }}(t) }{\mathrm {d} t^{\alpha }}+\frac{1}{LC}u_{C{\alpha }}(t)=\frac{1}{LC}e\left( t \right) ,\quad {\alpha },{\beta }\in {\mathbb {R}^{+}}, \end{aligned}$$
(4)

where:

$$\begin{aligned} R_{Z}=R_{S}+R_{C}+R_{L}. \end{aligned}$$
(5)

The solution of the above equation is possible using the Laplace transform, since the considered circuit is linear. Using the Laplace transform of a fractional derivative in the Caputo sense [18]:

$$\begin{aligned} \mathscr {L}\left\{ _{0}^{C}\text {D}_{t}^{{\alpha }}f(t) \right\} =s^{{\alpha }}F(s)-\sum _{k=0}^{n}s^{{\alpha }-k-1}f^{(k)}(0), \end{aligned}$$
(6)

for zero initial conditions, the transform of voltage across the ideal supercapacitor \({C}_{\alpha }\) is given by a formula:

$$\begin{aligned} U_{C{\alpha }}(s)=\frac{1}{LC} \frac{E(s)}{s^{{\alpha }+{\beta }}+\frac{R_{Z}}{L}s^{{\alpha }}+ \frac{1}{LC}}. \end{aligned}$$
(7)

The Laplace transform of current I(s) flowing in the circuit is defined by a formula:

$$\begin{aligned} I(s)=\frac{E(s)}{L}\frac{s^{{\alpha }}}{s^{{\alpha }+{\beta }}+ \frac{R_{Z}}{L}s^{{\alpha }}+\frac{1}{LC}}. \end{aligned}$$
(8)

Furthermore, the transform of the voltage across the real supercapacitor \({U}_{C}\)(s) (including its series resistance \({R}_{C}\), see Fig. 1) is given by:

$$\begin{aligned} U_{C}(s)=\frac{1}{LC}E(s)\frac{CR_{C}s^{\alpha }+1}{s^{{\alpha } +{\beta }}+\frac{R_{Z}}{L}s^{{\alpha }}+\frac{1}{LC}}, \end{aligned}$$
(9)

while the transform of the voltage U \(_{L{\beta }}\)(s) across the ideal fractional-order inductance is:

$$\begin{aligned} U_{L{\beta }}(s)=E(s)\left( 1-\frac{\frac{R_{Z}}{L}s^{{\alpha }}+\frac{1}{LC}}{s^{{\alpha }+ {\beta }}+\frac{R_{Z}}{L}s^{{\alpha }}+\frac{1}{LC}} \right) , \end{aligned}$$
(10)

whereas the transform of the voltage across the real fractional-order inductance \({U}_{L}\)(s) (including \({R}_{L}\)) can be written as:

$$\begin{aligned} U_{L}(s)=E(s)\left( 1-\frac{\frac{R_{S}+R_{C}}{L}s^{{\alpha }}+\frac{1}{LC}}{s^{{\alpha }+{\beta }}+\frac{R_{Z}}{L}s^{{\alpha }}+\frac{1}{LC}} \right) . \end{aligned}$$
(11)

The method of determining originals of (7)–(11), i.e., time waveforms occurring in the circuit from Fig. 1, is described next.

3 Method of Solving the Problem

Solution of the problem can be achieved by using the method of rational function into partial fraction decomposition [16]. Formulae (7)–(11) can be written in a general form:

$$\begin{aligned} F(s)=\frac{Y(s)}{E(s)}=\frac{As^{\alpha }+B}{s^{{\alpha }+ {\beta }}+as^{{\alpha }}+b}, \quad {\alpha }, {\beta }\in {\mathbb {R^{+}}}, \end{aligned}$$
(12)

where:

$$\begin{aligned} \begin{aligned} E(s)&=\mathscr {L}\left\{ e(t) \right\} ,\\ Y(s)&=\mathscr {L}\left\{ u_{C{\alpha }}(t) \right\} \, \text {or} \,\mathscr {L}\left\{ u_{C}(t) \right\} \, \text {or} \, \\&\quad \mathscr {L}\left\{ i(t) \right\} \, \text {or} \, \mathscr {L}\left\{ u_{L{\beta }}(t) \right\} \, \text {or} \, \mathscr {L}\left\{ u_{L}(t) \right\} . \end{aligned} \end{aligned}$$
(13)

In case the rational function (12) is an improper fraction, by dividing the polynomial of numerator by the polynomial of denominator, consequently the function can be written in a form:

$$\begin{aligned} F(s)=\frac{Y(s)}{E(s)}=1-F_{1}(s)=1- \frac{A_{1}s^{\alpha }+B_{1}}{s^{{\alpha }+{\beta }}+as^{{\alpha }}+b}, \quad {\alpha }, {\beta }\in {\mathbb {R^{+}}}, \end{aligned}$$
(14)

from which relations (10) and (11) arise. Assuming that the parameters \({\alpha }\) and \({\beta }\) are rational numbers, they can always be represented in the form:

$$\begin{aligned} {\alpha }=\frac{m}{n}, \quad {\beta }=\frac{p}{n}, \quad m,n,p\in {\mathbb {N}}. \end{aligned}$$
(15)

By introducing a new variable:

$$\begin{aligned} w=s^{\frac{1}{n}}, \end{aligned}$$
(16)

relation (12) can be written as:

$$\begin{aligned} F(w)=\frac{Aw^{m}+B}{w^{n_{1}}+a w^{m}+b}. \end{aligned}$$
(17)

where: \({n}_1 = {m} + {p}\).

The function \({F}_{1}\)(w) can be written similarly.

It should be noted that the response of the system described by the transfer function F(s) does not have to be BIBO stable (bounded input, bounded output). It can be proved [15, 16] that if the poles of the function F(w) are placed on the s-complex plane outside the cone of aperture angle \({\alpha }=\frac{{\pi }}{2n}\), then this system is BIBO stable. The concerned cone has a vertex at the origin of the coordinate system and is located symmetrically around the semi-axis Re\(\{{s}\}, {s}\ge 0\). In the specific case, position of the poles depends on the system parameters \({\alpha }, {\beta }, {R}_{S}, {R}_{C}, {R}_{L}\), L, C and it requires a separate analysis. Function F(w) is a classic rational function of the complex variable w. The function has, in general, \({k}_1\) real poles and \(2{k_2}\) complex conjugate poles:

$$\begin{aligned} n_{1}=k_{1}+2k_{2}. \end{aligned}$$
(18)

Assuming that the function F(w) has only single poles, it can be expressed as a sum of partial fractions:

$$\begin{aligned} F(w)=\sum _{i=1}^{k_{1}}\frac{R_{i}}{w-w_{i}}+\sum _{j=1}^{k_{2}}\left( \frac{C_{j}}{w-w_{j}}+\frac{C_{j}^{*}}{w-w_{j}^{*}} \right) , \end{aligned}$$
(19)

where \({w}_i\)—real poles, \({w}_j,{w}_{j}^{*}\)—complex conjugate poles, \({R}_i, {C}_{j}, {C}_{j}^{*}\)—decomposition coefficients (residues).

Returning to the Laplace domain, function F(s) expressed as a sum of partial fractions is:

$$\begin{aligned} F(s)=\sum _{i=1}^{k_{1}}\frac{R_{i}}{s^{\frac{1}{n}}-w_{i}}+\sum _{j=1}^{k_{2}} \left( \frac{C_{j}}{s^{\frac{1}{n}}-w_{j}}+\frac{C_{j}^{*}}{s^{\frac{1}{n}} -w_{j}^{*}}\right) , \end{aligned}$$
(20)

where all the coefficients remain the same as in Eq. (19). The inverse transform of function F(s) has been determined using Borel convolution theorem and the following relation [16]:

$$\begin{aligned} \mathscr {L}^{-1}\left\{ \frac{k!s^{{\nu }-{\mu }}}{\left( s^{\nu }\pm a \right) ^{(k+1)}} \right\} =t^{{\nu } k+{\mu }-1}E_{{\nu },{\mu }}^{(k)}\left( \mp at^{\nu }\right) , \; k\in {\mathbb {N}}, \text {Re}\left\{ s \right\} > \left| a \right| ^{{\nu } ^{-1}}, \end{aligned}$$
(21)

where: \({E}_{{\nu },{\mu }}^{(k)}(\mp at^{\nu })\)—classic kth-order two-parameter Mittag-Leffler function derivative [18].

Using the presented method, current and voltage waveforms in the considered circuit from Fig. 1 can be determined.

4 Solution of the Problem

4.1 Case of Real Poles

In this section, we assume that the function F(w) has \({k}_1\) real poles (\({n}_1 = {k}_1\)). In this case, the Laplace transform \({U}_{C{\alpha }}\)(s) of the voltage across the ideal supercapacitor is given by:

$$\begin{aligned} U_{C{\alpha }}(s)_{\text {real}}=\frac{1}{LC}E(s) \sum _{i=1}^{k_{1}}\frac{R_{i}}{s^{\lambda } -w_{i}}, \end{aligned}$$
(22)

where: \({\lambda } = \frac{1}{n}\),

$$\begin{aligned} u_{C{\alpha }}(t)_{\text {real}}=\mathscr {L}^{-1}\left\{ U_{C{\alpha }}(s)\right\} = \frac{1}{LC}\sum _{i=1}^{k_{1}}R_{i}\int _{0}^{t}e(t-{\tau }){\tau }^{{\lambda }-1}E_{{\lambda },{\lambda }}\left( w_{i}{\tau }^{\lambda } \right) \mathrm {d}{\tau }. \end{aligned}$$
(23)

Similarly:

$$\begin{aligned} I(s)_{\text {real}}=\frac{1}{L}E(s)\sum _{i=1}^{k_{1}} \frac{S_{i}}{s^{\lambda } -w_{i}}, \end{aligned}$$
(24)

and:

$$\begin{aligned} i(t)_{\text {real}}=\mathscr {L}^{-1}\left\{ I(s)\right\} = \frac{1}{L}\sum _{i=1}^{k_{1}}S_{i}\int _{0}^{t}e (t-{\tau }){\tau }^{{\lambda }-1}E_{{\lambda },{\lambda }}\left( w_{i}{\tau }^{\lambda } \right) \mathrm {d}{\tau }. \end{aligned}$$
(25)

The transform of the voltage across the real supercapacitor (see Fig. 1) is defined by a formula:

$$\begin{aligned} U_{C}(s)_{\text {real}}= \frac{1}{LC}E(s)\sum _{i=1}^{k_{1}}\frac{T_{i}}{s^{\lambda } -w_{i}}, \end{aligned}$$
(26)

hence:

$$\begin{aligned} u_{C}(t)_{\text {real}}=\mathscr {L}^{-1}\left\{ U_{C}(s)\right\} =\frac{1}{LC}\sum _{i=1}^{k_{1}}T_{i}\int _{0}^{t}e (t-{\tau }){\tau }^{{\lambda }-1}E_{{\lambda },{\lambda }}\left( w_{i}{\tau }^{\lambda } \right) \mathrm {d}{\tau }. \end{aligned}$$
(27)

Analogously, the voltage across the ideal fractional-order inductance can be determined:

$$\begin{aligned} U_{L{\beta }}(s)_{\text {real}}=E(s) - E(s)\sum _{i=1}^{k_{1}}\frac{U_{i}}{s^{\lambda } -w_{i}}, \end{aligned}$$
(28)

and:

$$\begin{aligned} u_{L{\beta }}(t)_{\text {real}}= & {} \mathscr {L}^{1}\left\{ U_{L{\beta }}(s)\right\} \nonumber \\= & {} e(t)-\sum _{i=1}^{k_{1}}U_{i}\int _{0}^{t}e(t-{\tau }){\tau }^{{\lambda }-1}E_{{\lambda },{\lambda }}\left( w_{i}{\tau }^{\lambda } \right) \mathrm {d}{\tau }, \end{aligned}$$
(29)

as well as the voltage across the real fractional-order coil (Fig. 1):

$$\begin{aligned} U_{L}(s)_{\text {real}}=E(s) - E(s)\sum _{i=1}^{k_{1}}\frac{W_{i}}{s^{\lambda } -w_{i}}, \end{aligned}$$
(30)

and:

$$\begin{aligned} u_{L}(t)_{\text {real}}=\mathscr {L}^{1}\left\{ U_{L}(s)\right\} = e(t)-\sum _{i=1}^{k_{1}}W_{i}\int _{0}^{t}e(t-{\tau }){\tau }^{{\lambda }-1}E_{{\lambda },{\lambda }}\left( w_{i}{\tau }^{\lambda } \right) \mathrm {d}{\tau }. \end{aligned}$$
(31)

Symbols \({R_i}, T_i, S_i, U_i, W_i\) occurring in the above formulae are the appropriate partial fraction decomposition coefficients (residues) of the relations (7)–(11).

4.2 Case of Complex Conjugate Poles

Assuming that the function F(w) has only \(2{k}_{2} ({n}_{1} = 2{k}_{2}\)) complex conjugate poles, the Laplace transform of the voltage on the ideal supercapacitor is described by a formula:

$$\begin{aligned} U_{C{\alpha }}(s)_{\text {complex}}=\frac{1}{LC} E(s)\sum _{j=1}^{k_{2}}\left( \frac{C_{j}}{s^{\lambda } -w_{j}}+\frac{C_{j}^{*}}{s^{\lambda } -w_{j}^{*}} \right) . \end{aligned}$$
(32)

Using Borel convolution theorem, formula (21) and Mittag-Leffler function representation as a series [18], the voltage across the ideal supercapacitor is defined by a relation:

$$\begin{aligned} \begin{aligned} u_{C{\alpha }}(t)_{\text {complex}}&=\mathscr {L}^{-1}\left\{ U_{C{\alpha }}(s)_{\text {complex}} \right\} \\&=\frac{1}{LC}\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| C_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \varphi +k\vartheta \right) }{\varGamma ({\lambda }(k+1))} \int _{0}^{t}e(t-{\tau }){\tau }^{{\lambda }(k+1)-1}\mathrm {d}{\tau }, \end{aligned} \end{aligned}$$
(33)

where:

$$\begin{aligned} {\varphi }= & {} \text {arctg}\left( \frac{\text {Im}\left\{ C_{j} \right\} }{\text {Re}\left\{ C_{j} \right\} }\right) , \end{aligned}$$
(34)
$$\begin{aligned} {\vartheta }= & {} \text {arctg}\left( \frac{\text {Im}\left\{ w_{j} \right\} }{\text {Re}\left\{ w_{j} \right\} }\right) . \end{aligned}$$
(35)

Following the analogous procedure, the current and voltages appearing in the circuit from Fig. 1 have been determined:

$$\begin{aligned} \begin{aligned} i(t)_{\text {complex}}&=\mathscr {L}^{-1}\left\{ I(s)_{\text {complex}} \right\} \\&= \frac{1}{L}\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| D_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \gamma +k\vartheta \right) }{\varGamma ({\lambda }(k+1))} \int _{0}^{t}e(t-{\tau }){\tau }^{{\lambda }(k+1)-1}\mathrm {d}{\tau }, \end{aligned} \end{aligned}$$
(36)
$$\begin{aligned} \begin{aligned} u_{C}(t)_{\text {complex}}&=\mathscr {L}^{-1}\left\{ U_{C}(s)_{\text {complex}} \right\} \\&=\frac{1}{LC}\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| E_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \delta +k\vartheta \right) }{\varGamma ({\lambda }(k+1))} \int _{0}^{t}e(t-{\tau }){\tau }^{{\lambda }(k+1)-1}\mathrm {d}{\tau }, \end{aligned} \end{aligned}$$
(37)
$$\begin{aligned} \begin{aligned} u_{L{\beta }}(t)_{\text {complex}}&=\mathscr {L}^{-1}\left\{ U_{L{\beta }}(s)_{\text {complex}} \right\} \\&= e(t)-\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| F_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \eta +k\vartheta \right) }{\varGamma ({\lambda }(k+1))} \int _{0}^{t}e(t-{\tau }){\tau }^{{\lambda }(k+1)-1}\mathrm {d}{\tau }, \end{aligned} \end{aligned}$$
(38)
$$\begin{aligned} \begin{aligned} u_{L}(t)_{\text {complex}}&=\mathscr {L}^{-1}\left\{ U_{L}(s)_{\text {complex}} \right\} \\&= e(t)-\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| G_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \varepsilon +k\vartheta \right) }{\varGamma ({\lambda }(k+1))} \int _{0}^{t}e(t-{\tau }){\tau }^{{\lambda }(k+1)-1}\mathrm {d}{\tau }, \end{aligned}\nonumber \\ \end{aligned}$$
(39)

where: \(C_j, D_j, E_j, F_j, G_j\)—appropriate complex partial fraction decomposition coefficients (residues) of relations (7)–(11), \({\varphi }, {\gamma }, {\delta }, {\eta }, {\varepsilon }\)—arguments of the complex coefficients \(C_j, D_j, E_j, F_j, G_j\) calculated analogously to formulae (34)–(35).

If the function F(s) (or \({F}_{1}\)(s)) contains real and complex conjugate poles, then the current and voltages are a sum of the relations derived in Sects. 4.1 and 4.2 of the paper.

5 Solution for Specific Waveform Cases

In specific cases, convolution integrals expressing the current and voltages in the circuit from Fig. 1 (see Sect. 4) can be presented in a closed form. It is possible, when the forcing voltage is a constant waveform E, or is expressed by a Fourier series. Several of such cases have been considered below.

5.1 Constant Forcing Voltage e(t) = E = const.

In this case, the current and voltage waveforms in the considered circuit are described by relations:

$$\begin{aligned} u_{C{\alpha }}(t)_{\text {real}}= & {} \frac{E}{LC}t^{\lambda }\sum _{i=1}^{k_{1}}R_{i}\sum _{k=0}^{\infty }\frac{\left( w_{i}t^{\lambda } \right) ^{k}}{\varGamma \left( {\lambda }\left( k+1 \right) +1 \right) }, \end{aligned}$$
(40)
$$\begin{aligned} u_{C{\alpha }}(t)_{\text {complex}}= & {} \frac{E}{LC}t^{\lambda }\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| C_{j} \right| \text {cos}\left( \gamma +k\vartheta \right) }{\varGamma ({\lambda }(k+1)+1)}\left( \left| w_{j}\right| {t}^{\lambda } \right) ^{k}, \end{aligned}$$
(41)
$$\begin{aligned} i(t)_{\text {real}}= & {} \frac{E}{L}t^{\lambda }\sum _{i=1}^{k_{1}}S_{i}\sum _{k=0}^{\infty }\frac{ \left( w_{i}t^{\lambda } \right) ^{k}}{\varGamma \left( {\lambda }(k+1)+1 \right) }, \end{aligned}$$
(42)
$$\begin{aligned} i(t)_{\text {complex}}= & {} \frac{E}{L}t^{\lambda }\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| D_{j} \right| \text {cos}\left( \gamma +k\vartheta \right) }{\varGamma ({\lambda }(k+1)+1)}\left( \left| w_{j}\right| t^{\lambda } \right) ^{k}, \end{aligned}$$
(43)
$$\begin{aligned} u_{C}(t)_{\text {real}}= & {} \frac{E}{LC}t^{\lambda }\sum _{i=1}^{k_{1}}T_{i}\sum _{k=0}^{\infty }\frac{\left( w_{i}t^{\lambda } \right) ^{k}}{\varGamma \left( {\lambda }\left( k+1 \right) +1 \right) }, \end{aligned}$$
(44)
$$\begin{aligned} u_{C}(t)_{\text {complex}}= & {} \frac{E}{LC}t^{\lambda }\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| E_{j} \right| \text {cos}\left( \delta +k\vartheta \right) }{\varGamma ({\lambda }(k+1)+1)}\left( \left| w_{j}\right| t^{\lambda } \right) ^{k}, \end{aligned}$$
(45)
$$\begin{aligned} u_{L{\beta }}(t)_{\text {real}}= & {} E-Et^{\lambda }\sum _{i=1}^{k_{1}}U_{i}\sum _{k=0}^{k_{1}}\frac{\left( w_{i}{\tau }^{\lambda } \right) ^{k}}{\varGamma \left( {\lambda }\left( k+1 \right) +1 \right) }, \end{aligned}$$
(46)
$$\begin{aligned} u_{L{\beta }}(t)_{\text {complex}}= & {} E-Et^{\lambda }\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| F_{j} \right| \text {cos}\left( \eta +k\vartheta \right) }{\varGamma ({\lambda }(k+1)+1)}\left( \left| w_{j}\right| t^{\lambda } \right) ^{k}, \end{aligned}$$
(47)
$$\begin{aligned} u_{L}(t)_{\text {real}}= & {} E-Et^{\lambda }\sum _{i=1}^{k_{1}}W_{i}\sum _{k=0}^{k_{1}}\frac{\left( w_{i}{\tau }^{\lambda } \right) ^{k}}{\varGamma \left( {\lambda }\left( k+1 \right) +1 \right) }, \end{aligned}$$
(48)
$$\begin{aligned} u_{L}(t)_{\text {complex}}= & {} E-Et^{\lambda }\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| G_{j} \right| \text {cos}\left( \varepsilon +k\vartheta \right) }{\varGamma ({\lambda }(k+1)+1)}\left( \left| w_{j}\right| t^{\lambda } \right) ^{k}. \end{aligned}$$
(49)

5.2 Monoharmonic Forcing Voltage

When the voltage source is described by a formula:

$$\begin{aligned} e(t) = \left| E_{m} \right| \text {sin}({\omega }t +\phi )= A\text {sin}({\omega }t) + B \text {cos}({\omega }t), \end{aligned}$$
(50)

where:

$$\begin{aligned} A= & {} \left| E_{m} \right| \text {cos}{\phi }, \end{aligned}$$
(51)
$$\begin{aligned} B= & {} \left| E_{m} \right| \text {sin}{\phi }, \end{aligned}$$
(52)

then the current and voltage waveforms in the circuit from Fig. 1 are defined by formulae:

$$\begin{aligned} u_{C{\alpha }}(t)_{\text {real}}= & {} \frac{1}{LC}\sum _{i=1}^{k_{1}}R_{i}\sum _{k=0}^{\infty }\frac{w_{i}^{k}}{\varGamma \left( {\lambda }\left( k+1 \right) \right) }\theta \left( t,k \right) , \end{aligned}$$
(53)
$$\begin{aligned} i(t)_{\text {real}}= & {} \frac{1}{L}\sum _{i=1}^{k_{1}}S_{i}\sum _{k=0}^{\infty }\frac{ w_{i}^{k}}{\varGamma \left( {\lambda }(k+1) \right) }\theta (t,k), \end{aligned}$$
(54)
$$\begin{aligned} u_{C}(t)_{\text {real}}= & {} \frac{1}{LC}\sum _{i=1}^{k_{1}}T_{i}\sum _{k=0}^{\infty }\frac{w_{i}^{k}}{\varGamma \left( {\lambda }\left( k+1 \right) \right) }{\theta }(t,k), \end{aligned}$$
(55)
$$\begin{aligned} u_{L{\beta }}(t)_{\text {real}}= & {} A\, \text {sin}({\omega }t)+B\, \text {cos}({\omega }t)\nonumber \\&-\sum _{i=1}^{k_{1}}U_{i}\sum _{k=0}^{\infty }\frac{w_{i}^{k}}{\varGamma \left( {\lambda }\left( k+1 \right) \right) }{\theta } (t,k), \end{aligned}$$
(56)
$$\begin{aligned} u_{L}(t)_{\text {real}}= & {} A\, \text {sin}({\omega }t)+B\, \text {cos}({\omega }t)\nonumber \\&-\sum _{i=1}^{k_{1}}W_{i}\sum _{k=0}^{\infty }\frac{w_{i}^{k}}{\varGamma \left( {\lambda }\left( k+1 \right) \right) }{\theta } (t,k), \end{aligned}$$
(57)

where:

$$\begin{aligned} \begin{aligned} {\theta }(t,k)&=\left( A\text {cos}\left( {\omega }t \right) + B \text {sin}\left( {\omega }t \right) \right) \frac{t^{{\lambda }(k+1)}}{{\lambda }(k+1)}\\&\quad \cdot _{p}{F}_{q}\left( \frac{{\lambda }(k+1)}{2};\frac{1}{2}, 1+\frac{{\lambda (k+1)}}{2};-\frac{1}{4}t^2{\omega }^2 \right) \\&\quad + \left( A\text {sin}\left( {\omega }t \right) - B\text {cos}\left( {\omega }t \right) \right) \frac{{\omega }t^{{\lambda }(k+1)+1}}{{\lambda }(k+1)+1}\\&\quad \cdot _{p}{F}_{q}\left( \frac{1+{\lambda }(k+1)}{2};\frac{3}{2}, \frac{3+{\lambda (k+1)}}{2};-\frac{1}{4}t^2{\omega }^2 \right) . \end{aligned} \end{aligned}$$
(58)

and:

$$\begin{aligned} u_{C{\alpha }}(t)_{\text {complex}}= & {} \frac{1}{LC}\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| C_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \varphi +k\vartheta \right) }{\varGamma ({\lambda }(k+1))}\theta (t,k), \end{aligned}$$
(59)
$$\begin{aligned} i(t)_{\text {complex}}= & {} \frac{1}{L}\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| D_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \gamma +k\vartheta \right) }{\varGamma ({\lambda }(k+1))}{\theta }(t,k), \end{aligned}$$
(60)
$$\begin{aligned} u_{C}(t)_{\text {complex}}= & {} \frac{1}{LC}\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| E_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \delta +k\vartheta \right) }{\varGamma ({\lambda }(k+1))}{\theta } (t,k), \end{aligned}$$
(61)
$$\begin{aligned} u_{L{\beta }}(t)_{\text {complex}}= & {} \left( A\text {sin}\left( {\omega }t \right) + B \text {cos}\left( {\omega }t \right) \right) \nonumber \\&-\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| F_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \eta +k\vartheta \right) }{\varGamma ({\lambda }(k+1))}{\theta (t,k)}, \end{aligned}$$
(62)
$$\begin{aligned} u_{L}(t)_{\text {complex}}= & {} \left( A\text {sin}\left( {\omega }t \right) + B \text {cos}\left( {\omega }t \right) \right) \nonumber \\&-\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2\left| G_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \varepsilon +k\vartheta \right) }{\varGamma ({\lambda }(k+1))}{\theta (t,k)}, \end{aligned}$$
(63)

where: \({\theta }\)(t,k) is a function given by formula (58) except that the summation of partial fraction poles extends from \(j = 1\) to \(j = k_{2}\).

5.3 Polyharmonic Forcing Voltage

In case of T-periodic voltage source, described by a classic Fourier series:

$$\begin{aligned} e(t)= & {} E_{0}+\sum _{h=1}^{\infty }|E_{mh}|\text {cos}\left( h{\omega }_{0}t +{\varphi }_{h} \right) \nonumber \\= & {} E_{0}+ \sum _{h=1}^{\infty }\left( A_{h}\text {cos}\left( h{\omega }_{0}t \right) +B_{h}\text {sin}\left( h{\omega }_{0}t \right) \right) , \end{aligned}$$
(64)

where:

$$\begin{aligned} A_{h}= & {} |E_{mh}|\text {sin}({\varphi }_{h}), \end{aligned}$$
(65)
$$\begin{aligned} B_{h}= & {} |E_{mh}|\text {cos}({\varphi }_{h}), \end{aligned}$$
(66)

waveforms of the voltages and the current are as follows:

$$\begin{aligned} u_{C{\alpha }}(t)_{\text {real}}= & {} \frac{1}{LC}\sum _{i=1}^{k_{1}}R_{i}\sum _{k=0}^{\infty }w_{i}^{k}\;\psi \left( t,h, k \right) , \end{aligned}$$
(67)
$$\begin{aligned} i(t)_{\text {real}}= & {} \frac{1}{L}\sum _{i=1}^{k_{1}}S_{i}\sum _{k=0}^{\infty } w_{i}^{k}\;\psi (t,h,k), \end{aligned}$$
(68)
$$\begin{aligned} u_{C}(t)_{\text {real}}= & {} \frac{1}{LC}\sum _{i=1}^{k_{1}}T_{i}\sum _{k=0}^{\infty }w_{i}^{k}\,{\psi }(t,h,k), \end{aligned}$$
(69)
$$\begin{aligned} u_{L{\beta }}(t)_{\text {real}}= & {} E_{0} +\sum _{h=1}^{\infty }(A_{h}\, \text {sin}(h{\omega }_{0}t)+B_{h}\, \text {cos}(h{\omega _{0}}t))\nonumber \\&-\sum _{i=1}^{k_{1}}U_{i}\sum _{k=0}^{\infty }w_{i}^{k}{\psi } (t,h,k), \end{aligned}$$
(70)
$$\begin{aligned} u_{L}(t)_{\text {real}}= & {} E_{0} +\sum _{h=1}^{\infty }(A_{h}\, \text {sin}(h{\omega }_{0}t)+B_{h}\, \text {cos}(h{\omega _{0}}t))\nonumber \\&-\sum _{i=1}^{k_{1}}W_{i}\sum _{k=0}^{\infty }w_{i}^{k}{\psi } (t,h,k), \end{aligned}$$
(71)

where:

$$\begin{aligned} {\psi }(t,h,k)= & {} \frac{E_{0}t^{{\lambda }k}}{\varGamma ({\lambda }(k+1)+1)}\nonumber \\&+\sum _{h=1}^{\infty }\left( A_{h}\text {cos}\left( h{\omega }_{0}t \right) + B_{h} \text {sin}\left( h{\omega }_{0}t \right) \right) \frac{t^{{\lambda }(k+1)}}{{\varGamma }({\lambda }(k+1)+1)}\nonumber \\&\cdot _{p}{F}_{q}\left( \frac{{\lambda }(k+1)}{2};\frac{1}{2}, \frac{{\lambda (k+1)}}{2};-\frac{1}{4}h^{2}{\omega }_{0}^{2}t^{2} \right) \nonumber \\&+ \left( A_{h}\text {sin}\left( h{\omega }_{0}t \right) - B_{h}\text {cos}\left( h{\omega }_{0}t \right) \right) \frac{{\omega }t^{{\lambda }(k+1)+1}}{{\varGamma }({\lambda }(k+1))} \frac{{\omega }_{0}h}{1+{\lambda }(k+1)}\nonumber \\&\cdot _{p}{F}_{q} \left( \frac{1+{\lambda }(k+1)}{2};\frac{3}{2}, \frac{3+{\lambda }(k+1)}{2}; -\frac{1}{4}h^{2} {\omega }_{0}^{2} t^{2}\right) , \end{aligned}$$
(72)
$$\begin{aligned} u_{C{\alpha }}(t)_{\text {complex}}= & {} \frac{1}{LC}\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }2\left| C_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \varphi +k\vartheta \right) \psi (t,h,k), \end{aligned}$$
(73)
$$\begin{aligned} i(t)_{\text {complex}}= & {} \frac{1}{L}\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }2\left| D_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \gamma +k\vartheta \right) {\psi } (t,h,k), \end{aligned}$$
(74)
$$\begin{aligned} u_{C}(t)_{\text {complex}}= & {} \frac{1}{LC}\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }2\left| E_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \delta +k\vartheta \right) {\psi } (t,h,k), \end{aligned}$$
(75)
$$\begin{aligned} u_{L{\beta }}(t)_{\text {complex}}= & {} E_{0}+\sum _{h=1}^{\infty }\left( A_{h}\text {sin}\left( h{\omega }_{0}t \right) + B_{h} \text {cos}\left( h{\omega }_{0}t \right) \right) \nonumber \\&-\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }2\left| F_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \eta +k\vartheta \right) {\psi (t,h,k)}, \end{aligned}$$
(76)
$$\begin{aligned} u_{L}(t)_{\text {complex}}= & {} E_{0}+\sum _{h=1}^{\infty }\left( A_{h}\text {sin}\left( h{\omega }_{0}t \right) + B_{h} \text {cos}\left( h{\omega }_{0}t \right) \right) \nonumber \\&-\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }2\left| G_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \varepsilon +k\vartheta \right) {\psi (t,h,k)}, \end{aligned}$$
(77)

where: \({\psi }({t},{h},{k})\) is a function defined by formula (72), but the summation of partial fraction poles extends from \(j = 1\) to \({j} = k_{2}\).

It should be noted that the above equations are also true when the voltage source has an almost-periodic waveform and has a spectrum defined for \({\varLambda }=\left\{ {\omega }_{h}\right\} _{h\in \mathbb {N}}\) which is countable or is a finite set of frequencies \({\omega }_{h}\). Appropriate dependencies can be obtained by substitution \({h}{\omega }_{0}\rightarrow {\omega }_{h}, {h}\in \mathbb {N}\). Such waveforms appear often in modulation systems.

5.4 Forcing Voltage is an Element of a Hilbert Space

Assuming that the voltage source e(t) is an element of any Hilbert space with a norm \(\left\| \cdot \right\| _{H}\), a scalar product \(\left( \cdot ,\cdot \right) _{H}\) and a basis \(\left\{ e_{h} \right\} , \textit{h}\in {\mathbb {N}}\), it can always be expressed as a generalized Fourier series:

$$\begin{aligned} e(t)=\sum _{h=0}^{\infty }{\xi }_{h}e_{h}(t), \end{aligned}$$
(78)

wherein:

$$\begin{aligned} {\xi }_{h}= \left( e(t), e_{h}(t) \right) _{H},\quad h\in {\mathbb {N}}. \end{aligned}$$
(79)

Formulae describing the current and voltage waveforms in the circuit from Fig. 1 are given as follows:

$$\begin{aligned} u_{C{\alpha }}(t)_{\text {real}}= & {} \frac{1}{LC}\sum _{i=1}^{k_{1}}\sum _{h=0}^{\infty }R_{i}{\xi }_{h}\int _{0}^{t}e_{h}(t-{\tau }){\tau }^{{\lambda }-1}E_{{\lambda },{\lambda }}\left( w_{i}{\tau }^{\lambda } \right) \mathrm {d}{\tau }, \end{aligned}$$
(80)
$$\begin{aligned} u_{C{\alpha }}(t)_{\text {complex}}= & {} \frac{1}{LC} \sum _{j=1}^{k_{2}} \sum _{k=0}^{\infty } \sum _{h=0}^{\infty }\frac{2{\xi }_{h}\left| C_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \varphi +k\vartheta \right) }{\varGamma ({\lambda }(k+1))}\nonumber \\&\times \int _{0}^{t}e_{h}(t-{\tau }){\tau }^{{\lambda }(k+1)-1}\mathrm {d}{\tau }, \end{aligned}$$
(81)
$$\begin{aligned} i(t)_{\text {real}}= & {} \frac{1}{L}\sum _{i=1}^{k_{1}}\sum _{h=0}^{\infty }S_{i}{\xi }_{h}\int _{0}^{t}e_{h}(t-{\tau }){\tau }^{{\lambda }-1}E_{{\lambda },{\lambda }}\left( w_{i}{\tau }^{\lambda } \right) \mathrm {d}{\tau }, \end{aligned}$$
(82)
$$\begin{aligned} i(t)_{\text {complex}}= & {} \frac{1}{L}\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\sum _{h=0}^{\infty }\frac{2{\xi }_{h}\left| D_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \gamma +k\vartheta \right) }{\varGamma ({\lambda }(k+1))}\nonumber \\&\times \int _{0}^{t}e_{h}(t-{\tau }){\tau }^{{\lambda }(k+1)-1}\mathrm {d}{\tau }, \end{aligned}$$
(83)
$$\begin{aligned} u_{C}(t)_{\text {real}}= & {} \frac{1}{LC}\sum _{i=1}^{k_{1}}\sum _{h=0}^{\infty }T_{i}{\xi }_{h}\int _{0}^{t}e_{h}(t-{\tau }){\tau }^{{\lambda }-1}E_{{\lambda },{\lambda }}\left( w_{i}{\tau }^{\lambda } \right) \mathrm {d}{\tau }, \end{aligned}$$
(84)
$$\begin{aligned} u_{C}(t)_{\text {complex}}= & {} \frac{1}{LC}\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\sum _{h=0}^{\infty }\frac{2{\xi }_{h}\left| E_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \delta +k\vartheta \right) }{\varGamma ({\lambda }(k+1))}\nonumber \\&\times \int _{0}^{t}e_{h}(t-{\tau }){\tau }^{{\lambda }(k+1)-1}\mathrm {d}{\tau }, \end{aligned}$$
(85)
$$\begin{aligned} u_{L{\beta }}(t)_{\text {real}}= & {} \sum _{h=0}^{\infty } {\xi }_{h}e_{h}(t)-\sum _{i=1}^{k_{1}}\sum _{h=0}^{\infty }U_{i}{\xi }_{h}\int _{0}^{t}e(t-{\tau }){\tau }^{{\lambda }-1}E_{{\lambda },{\lambda }}\left( w_{i}{\tau }^{\lambda } \right) \mathrm {d}{\tau },\nonumber \\ \end{aligned}$$
(86)
$$\begin{aligned} u_{L{\beta }}(t)_{\text {complex}}= & {} \sum _{h=0}^{\infty }{\xi }_{h}e_{h}(t)- \sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\frac{2{\xi }_{h}\left| F_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \eta +k\vartheta \right) }{\varGamma ({\lambda }(k+1))}\nonumber \\&\times \int _{0}^{t}e(t-{\tau }){\tau }^{{\lambda }(k+1) -1}\mathrm {d}{\tau }, \end{aligned}$$
(87)
$$\begin{aligned} u_{L}(t)_{\text {real}}= & {} \sum _{h=0}^{\infty }{\xi }_{h}e_{h}(t)-\sum _{i=1}^{k_{1}}W_{i}{\xi }_{h}\nonumber \\&\times \int _{0}^{t}e_{h}(t-{\tau }){\tau }^{{\lambda }-1}E_{{\lambda },{\lambda }}\left( w_{i}{\tau }^{\lambda } \right) \mathrm {d}{\tau }, \end{aligned}$$
(88)
$$\begin{aligned} u_{L}(t)_{\text {complex}}= & {} \sum _{h=0}^{\infty }{\xi }_{h}e_{h}(t)-\sum _{j=1}^{k_{2}}\sum _{k=0}^{\infty }\sum _{h=0}^{\infty }\frac{2{\xi }_{h}\left| G_{j} \right| \left| w_{j}\right| ^{k} \text {cos}\left( \varepsilon +k\vartheta \right) }{\varGamma ({\lambda }(k+1))}\nonumber \\&\times \int _{0}^{t}e(t-{\tau }){\tau }^{{\lambda }(k+1) -1}\mathrm {d}{\tau }. \end{aligned}$$
(89)

It should be noted that expression of the integrals appearing in the above formulae and containing the basis functions \({e}_{h}, {h}\in {\mathbb {N}}\) in a closed form, is not always possible.

6 Example

Based on earlier studies, a simulation example of the transient state in a series circuit of the class \({RL}_{\beta }{C}_{\alpha }\), with a supercapacitor and a real, fractional-order coil, has been carried out. The following parameters of the circuit elements have been assumed: a supercapacitor of pseudocapacitance \({C}_{\alpha } = 10 \frac{F}{s^{1-{\alpha }}}\) and a series internal resistance \({R}_{C} = 0.1\,{{\Omega }}\), a real fractional-order coil of pseudoinductance \({L} = 1 H s^{1-{\beta }}\) and its series internal resistance \({R}_{L} = 0.1\,{{\Omega }}\). The series resistance has been assumed as \({R}_{S} = 0\,{{\Omega }}\); therefore, \({R}_{Z} = {R}_{S} + {R}_{C} + {R}_{L} = 0.2\,{{\Omega }}\). Coefficients of the fractional-order elements have been: \({\alpha } =~0.5, {\beta } = 0.25\). The series \({RL}_{\beta }{C}_{\alpha }\) circuit has been supplied by a DC voltage source E = 5 V. For the given parameters values, the function F(w) (formula (17)) takes the form:

$$\begin{aligned} F(w)=\frac{Aw^{2}+B}{w^{3}+0.1w^{2}+0.1}, \end{aligned}$$
(90)

where:

$$\begin{aligned} w = s^{\frac{1}{4}}. \end{aligned}$$
(91)

Function (90) has three poles: \({w}_{1} = -0.54\)—one real pole, \({w}_{2} = 0.17-0.39{j}\) and \({w}_{2}^{*}=0.17 + 0.39{j}\)—two complex conjugate poles. The relevant partial fractions decomposition coefficients of the voltages and current are (rounded to two decimal places):

  • for real poles: \({R}_{1} = 1.52, {S}_{1} = 0.44, {T}_{1} = 1.97, {U}_{1} = 0.24, {W}_{1} = 0.20\);

  • for complex conjugate poles: \({C}_{1} = -1.76 + 1.39{j}, {C}_{1}^{*} = -1.76-1.39{j}, {D}_{1} = 0.28-0.07{j}, {D}_{1}^{*} = 0.28 + 0.07{j}, {E}_{1} = -0.48 + 1.32{j}, {E}_{1}^{*} = -0.48-1.32{j}, {F}_{1} = -0.021 + 0.12{j}, {F}_{1}^{*} = -0.021 - 0.12{j}, {G}_{1} = -0.048 + 0.13{j}, {G}_{1}^{*} = -0.048 - 0.13{j}\).

Simulations of the voltages \({u}_{C{\alpha }}({t}), {u}_{C}({t}), {u}_{L{\beta }}({t}), {u}_{L}({t})\) and the current i(t) in the circuit were performed in Mathematica, Maple and PSpice programs. The rules of modeling systems and circuits with fractional-order elements in PSpice have been described in “Appendix.” The need for simulation studies using three different programs has resulted from the fact that algorithms used for these calculations are different. In PSpice in ABM mode, the system response is calculated as a convolution of impulse response of assigned function (90) with a given excitation (voltage or current). In Mathematica as well as in Maple, calculations have been performed with the use of formulae in the form of series. Procedures used to calculate the value of \({\varGamma }\)-Euler function in these programs are different. Illustrations of these waveforms are shown in Figs. 2, 3, 4, 5 and 6. For practical reasons, \({k}=2000\) elements were assumed in numerical computations (instead of \({\infty }\) in Mittag-Leffler function). Simulations have been performed for the circuit with fractional-order elements and for the classic case of the considered circuit, when \({\alpha }, {\beta } = 1\). Numerical studies have been proven by experimental researches. Measurements were taken for a circuit (see Fig. 1) including:

  • supercapacitor with parameters: \({C}_{\alpha } = 10.6 \frac{F}{s^{(1-{\alpha })}}, {\alpha } = 0.54, {R}_{C} = 0.09\,{{\Omega }}\) (Maxwell Technologies model BMOD0058E016B02),

  • coil with ferromagnetic core with parameters: \({L}_{\beta } = 0.973\hbox {Hs}^{(1-{\beta })}, {\beta } = 0.279, {R}_{L} = 0.15\,{{\Omega }}\)

  • series resistor \({R}_{S}\) with resistance equal to 1 \({{\Omega }}\).

Fig. 2
figure 2

Simulations of the voltage \({u}_{C{\alpha }}\)(t) performed in: a Mathematica, b Maple and c PSpice programs

Full size image
Fig. 3
figure 3

Simulations of the current i(t) performed in: a Mathematica, b Maple and c PSpice programs (experimental results included)

Full size image
Fig. 4
figure 4

Simulations of the voltage \({u}_{C}\)(t) performed in: a Mathematica, b Maple and c PSpice programs (experimental results included)

Full size image
Fig. 5
figure 5

Simulations of the voltage \({u}_{L{\beta }}\)(t) performed in: a Mathematica, b Maple and c PSpice programs

Full size image
Fig. 6
figure 6

Simulations of the voltage \({u}_{L}\)(t) performed in: a Mathematica, b Maple and c PSpice programs (experimental results included)

Full size image

As it can be seen from Figs. 2, 3, 4, 5 and 6, shapes of the voltage waveforms for voltages \({u}_{C{\alpha }}\)(t) and \({u}_{C}\)(t) and the current i(t) look the same for simulations performed in all programs. Small difference can be seen in the case of the voltages \({u}_{L{\beta }}\)(t) and \({u}_{L}\)(t). The voltage across the fractional-order coil decreases faster according to program PSpice than in Mathematica and Maple, which implemented formulae (40)–(49). This difference is difficult to explain, but may be caused by PSpice algorithm. Further analysis will be taken in the future to explain this effect. Experimental results show quite good correlation with results obtained in PSpice.

Another observation is, despite the fact that \({R}_{Z}< {R}_{k} = 2\sqrt{\frac{L}{C}}\), where R\(_{k}\) is the critical resistance, the process of charging the supercapacitor by the resistance and the inductance is aperiodical, because of the parameters values \({\alpha }\) and \({\beta } < 1\). In case of \({\alpha }, {\beta } = 1\), waveforms show the attenuated oscillating process of charging the capacitor. Relations describing transient waveforms simplify to the solutions of classic integer-order differential equation. As it can be seen from the waveforms from Figs. 2, 3, 4, 5 and 6, there are significant differences in current and voltage waveforms for LC elements of integer and fractional orders. This observation explains the main reason for application of fractional-order models.

7 Conclusions

Method of the analysis of transient states in a series circuit of the class \({RL}_{\beta }{C}_{\alpha }\) with fractional-order elements \({L}_{\beta }, {C}_{\alpha }, {\alpha },{\beta }\in \mathbb {R^{+}}\) and at any kind of forcing voltage has been proposed in this paper. The considered circuit can be described by a differential equation containing derivatives of fractional order in the Caputo sense. To solve this equation, the Laplace transform method has been used and the idea of rational function decomposition into partial fractions, originally proposed in [18] for fractional-order equations. Effective dependencies allowing the determination of the current and voltages waveforms in the system for a number of cases have been achieved. The first two of them concern the situation when the analyzed rational functions have real or complex poles. Further expressions present solutions of the problem for different forcing voltages: constant, sinusoidal, periodic and arbitrary, which is an element of a Hilbert space.

The obtained results have been illustrated by an example. An exemplary \({RL}_{\beta }{C}_{\alpha }\) circuit have been supplied by a DC voltage source. It can be noted from the example that simulations performed in Mathematica, Maple and PSpice for voltages across the supercapacitor \({u}_{C{\alpha }}\)(t), \({u}_{C}\)(t) and the current i(t) take the same values and waveforms for given circuit parameters values. In the case of voltages across the fractional-order coil, \({u}_{L{\beta }}\)(t) and \({u}_{L}\)(t) waveforms from Mathematica and Maple programs are the same, but they differ slightly from the results obtained in PSpice. PSpice shows that these voltages decrease more rapidly and faster than it would result from the analytical formulae. These differences are difficult to explain and may be caused by the difference of PSpice algorithm in ABM mode. However, experimental results show quite good correlation with results obtained in PSpice; therefore, it is supposed that PSpice algorithm describes fractional-order systems with a quite good precision. For given parameters \({\alpha }\) and \({\beta }\), in spite of the fact that the resistance \({R}_{Z} < {R}_{k} = 2\sqrt{\frac{L}{C}}\) is less than the critical resistance, achieved waveforms show that supercapacitor charging process has an aperiodic character. In case of \({\alpha }, {\beta } = 1\), waveforms show the attenuated oscillating process of charging the capacitor, as it is known from the classic circuit theory. The results of simulations and experiments presented in Sect. 6 show significant differences in current and voltage waveforms for LC elements of integer and fractional orders (see Fig. 1). This is the main reason for application of fractional-order models. By changing the values of \({\alpha }\) and \({\beta }\), without changing the basic circuit parameters—\({L}_{\beta }, {C}_{\alpha }\), transient state may have an oscillating, critical or aperiodic character.

As far as it is known, previously obtained results did not contain relations expressing the current and voltages in the analyzed circuit for arbitrary excitation voltages in a closed form.