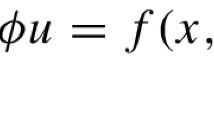Abstract
In this paper, we study the following logarithmic Schrödinger–Poisson system:
where \(\lambda >0\), \(V(x)\in C({\mathbb {R}}^3,{\mathbb {R}})\) and \(q(x)\ge 0\) for all \(x\in {\mathbb {R}}^3\). Under the suitable conditions on potential V(x) and q(x), by proceeding a new penalization scheme to the nonlocal term \(\phi \), combining with a new version of Minimax method, we prove the existence of positive solution \(u_{\lambda }\in H^1({\mathbb {R}}^3)\) of the above system for \(\lambda >0\) large enough. Moreover, we also investigate the concentration behavior of \(\{u_{\lambda }\}\) as \(\lambda \rightarrow +\infty \).
Similar content being viewed by others
References
Alves, C.O., Ji, C.: Multi-bump positive solutions for a logarithmic Schrödinger equation with deepening potential well. Sci. China Math. 64, 1577–1598 (2021)
Alves, C.O., de Morais Filho, D.C., Figueiredo, G.M.: On concentration of solution to a Schrödinger logarithmic equation with deepening potential well. Math. Methods Appl. Sci. 42, 4862–4875 (2019)
Alves, C.O., Gonçalves, J.V.A., Santos, J.A.: Existence of solution for a partial differential inclusion in \({\mathbb{R} }^N\) with steep potential well. Z. Angew. Math. Phys. 70, 41 (2019)
Alves, C.O., Ji, C.: Existence and concentration of positive solutions for a logarithmic Schrödinger equation via penalization method. Calc. Var. Partial. Differ. Equ. 59, 21 (2020)
Alves, C.O., De Morais Filho, D.C.: Existence and concentration of positive solutions for a Schrödinger logarithmic equation. Z. Angew. Math. Phys. 69, 144 (2018)
Azzollini, A., D’Avenia, P., Pomponio, A.: On the Schrödinger–Maxwell equations under the effect of a general nonlinear term. Ann. Inst. H. Poincaré Anal. Non Linéaire 27, 779–791 (2010)
Benci, V., Fortunato, D.: An eigenvalue problem for the Schrödinger–Maxwell equations. Topol. Methods Nonlinear Anal. 11, 283–293 (1998)
Benmlih, K.: Stationary solutions for a Schrödinger–Poisson system in \({\mathbb{R}}^3\). In: Proceedings of the 2002 Fez Conference on Partial Differential Equations, Electronic Journal of Differential Equations Conference, vol. 9, pp. 65–76 (2002)
Brézis, H., Kato, T.: Remarks on Schrödinger operator with singular complex potentials. J. Math. Pures Appl. 58, 137–151 (1979)
Cerami, G., Vaira, G.: Positive solutions for some non-autonomous Schrödinger–Poisson systems. J. Differ. Equ. 248, 521–543 (2010)
d’Avenia, P., Montefusco, E., Squassina, M.: On the logarithmic Schrödinger equation. Commun. Contemp. Math. 16, 1350032 (2014)
d’Avenia, P., Squassina, M., Zenari, M.: Fractional logarithmic Schrödinger equations. Math. Methods Appl. Sci. 38, 5207–5216 (2015)
Degiovanni, M., Zani, S.: Multiple solutions of semilinear elliptic equations with one-sided growth conditions, nonlinear operator theory. Math. Comput. Model. 32, 1377–1393 (2000)
Del Pino, M., Dolbeault, J.: The optimal Euclidean \(L^p\)-Sobolev logarithmic inequality. J. Funct. Anal. 197, 151–161 (2003)
Du, M.: Positive solutions for the Schrödinger–Poisson system with steep potential well. 16 July 2020. arXiv:2007.08088v1 [math.AP]
Del Pino, M., Felmer, P.L.: Local mountain pass for semilinear elliptic problems in undounded domain. Calc. Var. Partial Differ. Equ. 4, 121–137 (1996)
Gilbarg D., Trudinger N.S.: Elliptic Partial Differential Equations of Second Order, vol. 224, 2nd edn. Grundlehren der Mathematischen Wissenschaften. Springer, Berlin (1983)
Ji, C., Szulkin, A.: A logarithmic Schrödinger equation with asymptotic conditions on the potential. J. Math. Anal. Appl. 437, 241–254 (2016)
Jia, H.F., Luo, X.: Existence and concentrating behavior of solutions for Kirchhoff type equations with steep potential well. J. Math. Anal. Appl. 467, 893–915 (2018)
Jiang, Y.S., Zhou, H.S.: Schrödinger–Poisson system with steep potential well. J. Differ. Equ. 251, 582–608 (2011)
Li, N., He, X.: Existence and multiplicity results for some Schrödinger–Poisson system with critical growth. J. Math. Anal. Appl. 488, 124071 (2020)
Lions P.L.: The Concentration-Compactness Principle in the Calculus of Variations. The Locally Compact Case, Part 2 Anal. Inst. H. Poincaré, Sect. C 1, pp. 223–253 (1984)
Peng, X.Q., Jia, G., Huang, C.: Sign-changing solutions for modified Schrödinger–Poisson system with general nonlinearity. Complex Var. Elliptic Equ. (2021). https://doi.org/10.1080/17476933.2021.1947258
Ruiz, D.: The Schrödinger–Poisson equation under the effect of a nonlinear local term. J. Funct. Anal. 237, 655–674 (2006)
Rabinowitz, P.H.: Minimax Methods in Critical Points Theory with Application to Differential Equations, CBMS Regional Conference Series in Mathematics, Vol. 65. Am. Math. Soc. Providence (1986)
Squassina, M., Szulkin, A.: Multiple solutions to logarithmic Schrödinger equations with periodic potential. Cal. Var. Partial Differ. Equ. 54, 585–597 (2015)
Struwe, M.: Variational Methods, Applications to Nonlinear Partial Differential Equations and Hamiltonian Systems, 2nd edn. Springer, Berlin (1996)
Sun, J.T., Wu, T.F.: On the nonlinear Schrödinger–Poisson systems with sign-changing potential. Z. Angew. Math. Phys. 66, 1649–1669 (2015)
Sun, J.T., Wu, T.F.: Steep potential well may help Kirchhoff type equations to generate multiple solutions. Nonlinear Anal. 190, 111609 (2020)
Sun, J.T., Wu, T.F., Wu, Y.Z.: Existence of nontrivial solution for Schrödinger–Poisson systems with indefinite steep potential well. Z. Angew. Math. Phys. 68, 73 (2017)
Szulkin, A.: Minimax principles for lower semicontinuous functions and applications to nonlinear boundary value problems. Ann. Inst. H. Poincaré Anal. Non Linéaire 3, 77–109 (1986)
Tanaka, K., Zhang, C.: Multi-bump solutions for logarithmic Schrödinger equation. Cal. Var. Partial Differ. Equ. 56, 33 (2017)
Willem, M.: Minimax Theorems. Progress in Nonlinear Differential Equations and Their Applications, vol. 24. Birkhäuser Boston Inc., Boston (1996)
Xie, Q.L., Ma, S.W.: Existence and concentration of positive solutions for Kirchhoff-type problems with a steep well potential. J. Math. Anal. Appl. 431, 1210–1223 (2015)
Yin, L.F., Wu, X.P., Tang, C.L.: Existence and concentration of ground state solutions for critical Schrödinger–Poisson system with steep potential well. Appl. Math. Comput. 374, 125035 (2020)
Zhao, L., Liu, H., Zhao, F.: Existence and concentration of solutions for the Schrödinger–Poisson equations with steep well potential. J. Differ. Equ. 255, 1–23 (2013)
Zhang, X., Ma, S.W.: Multi-bump solutions of Schrödinger–Poisson equations with steep potential well. Z. Angew. Math. Phys. 66, 1615–1631 (2015)
Zloshchastiev, K.G.: Logarithmic nonlinearity in the theories of quantum gravity: origin of time and observational consequences. Grav. Cosmol. 16, 288–297 (2010)
Acknowledgements
X.Q. Peng is supported by the China Scholarship Council (No. 202208310170). G. Jia is supported by the National Natural Science Foundation of China (No. 11171220).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research is supported by the National Natural Science Foundation of China, Grant No. 11171220.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Peng, X., Jia, G. Existence and concentration behavior of solutions for the logarithmic Schrödinger–Poisson system with steep potential. Z. Angew. Math. Phys. 74, 29 (2023). https://doi.org/10.1007/s00033-022-01922-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00033-022-01922-6