Skip to main content
SpringerLink
Log in

Physics-Informed Neural Networks for rarefied-gas dynamics: Poiseuille flow in the BGK approximation

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

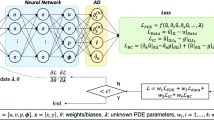
We present a new accurate approach to solving a class of problems in the theory of rarefied–gas dynamics using a Physics-Informed Neural Networks framework, where the solution of the problem is approximated by the constrained expressions introduced by the Theory of Functional Connections. The constrained expressions are made by a sum of a free function and a functional that always analytically satisfies the equation constraints. The free function used in this work is a Chebyshev neural network trained via the extreme learning machine algorithm. The method is designed to accurately and efficiently solve the linear one-point boundary value problem that arises from the Bhatnagar–Gross–Krook model of the Poiseuille flow between two parallel plates for a wide range of Knudsen numbers. The accuracy of our results is validated via the comparison with the published benchmarks.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Reynolds, O.: Xviii. on certain dimensional properties of matter in the gaseous state.-Part I. Experimental researches on thermal transpiration of gases through porous plates and on the laws of transpiration and impulsion, including an experimental proof that gas is not a continuous plenum.-part ii. on an extension of the dynamical theory of gas, which includes the stresses, tangential and normal, caused by a varying condition of gas, and affords an explanation of the phenomena of transpiration and impulsion. Philos. Trans. R. Soc. Lond. 170, 727–845 (1879)

    Google Scholar 

  2. Maxwell, J.C.: Iii. on stresses in rarefied gases arising from inequalities of temperature. Proc. R. Soc. Lond. 27(185–189), 304–308 (1878)

    MATH  Google Scholar 

  3. Knudsen, M.: Die gesetze der molekularströmung und der inneren reibungsströmung der gase durch röhren. Ann. Phys. 333(1), 75–130 (1909)

    Article  MATH  Google Scholar 

  4. Knudsen, M.: Thermischer molekulardruck der gase in röhren. Ann. Phys. 338(16), 1435–1448 (1910)

    Article  MATH  Google Scholar 

  5. Loyalka, S.: Comments on “poiseuille flow and thermal creep of a rarefied gas between parallel plates”.” Phys. Fluids 17(5), 1053–1055 (1974)

  6. Loyalka, S., Petrellis, N., Storvick, T.: Some exact numerical results for the BGK model: Couette, Poiseuille and thermal creep flow between parallel plates. Z. Angew. Math. Phys. ZAMP 30(3), 514–521 (1979)

    Article  MathSciNet  MATH  Google Scholar 

  7. Williams, M.: A review of the rarefied gas dynamics theory associated with some classical problems in flow and heat transfer. Z. Angew. Math. Phys. ZAMP 52(3), 500–516 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  8. Boffi, V., De Socio, L., Gaffuri, G., Pescatore, C.: Rigorous constructive solution to monodimensional poiseuille and thermal creep flows. Meccanica 11(4), 183–190 (1976)

    Article  MATH  Google Scholar 

  9. Cercignani, C.: The boltzmann equation. In: The Boltzmann Equation and its Applications, pp. 40–103. Springer, New york (1988)

    Chapter  MATH  Google Scholar 

  10. Sharipov, F.: Rarefied Gas Dynamics: Fundamentals for Research and Practice. Wiley, New Jersey (2015)

    Google Scholar 

  11. Ferziger, J., Kaper, H.: Mathematical theory of transport processes in gases. Am. J. Phys. 41(4), 601–603 (1973)

    Article  Google Scholar 

  12. Cercignani, C.: Theory and Application of the Boltzmann Equation. Scottish Academic Press, UK (1975)

    MATH  Google Scholar 

  13. Bhatnagar, P.L., Gross, E.P., Krook, M.: A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems. Phys. Rev. 94(3), 511 (1954)

    Article  MATH  Google Scholar 

  14. Shakhov, E.: Generalization of the krook kinetic relaxation equation. Fluid Dyn. 3(5), 95–96 (1968)

    Article  MathSciNet  Google Scholar 

  15. Loyalka, S.: Thermal transpiration in a cylindrical tube. Phys. Fluids 12(11), 2301–2305 (1969)

    Article  Google Scholar 

  16. Loyalka, S., Storvick, T.: Kinetic theory of thermal transpiration and mechanocaloric effect. III. Flow of a polyatomic gas between parallel plates. J. Chem. Phys. 71(1), 339–350 (1979)

    Article  Google Scholar 

  17. Chernyak, V., Porodnov, B., Suetin, P.: Application of the variational method to the problem of thermomolecular pressure difference in a cylindrical capillary. Inzh.-Fiz. Zh. 26, 446–450 (1974)

    Google Scholar 

  18. Valougeorgis, D., Thomas, J., Jr.: Exact numerical results for poiseuille and thermal creep flow in a cylindrical tube. Phys. Fluids 29(2), 423–429 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  19. Loyalka, S., Hickey, K.: Kinetic theory of thermal transpiration and the mechanocaloric effect: Planar flow of a rigid sphere gas with arbitrary accommodation at the surface. J. Vac. Sci. Technol. A Vac. Surf. Films 9(1), 158–163 (1991)

    Article  Google Scholar 

  20. Sharipov, F.: Rarefied gas flow through a long tube at any temperature ratio. J. Vac. Sci. Technol. A Vac. Surf. Films 14(4), 2627–2635 (1996)

    Article  Google Scholar 

  21. Ritos, K., Lihnaropoulos, Y., Naris, S., Valougeorgis, D.: Pressure-and temperature-driven flow through triangular and trapezoidal microchannels. Heat Transf. Eng. 32(13–14), 1101–1107 (2011)

    Article  Google Scholar 

  22. Ohwada, T., Sone, Y., Aoki, K.: Numerical analysis of the shear and thermal creep flows of a rarefied gas over a plane wall on the basis of the linearized boltzmann equation for hard-sphere molecules. Phys. Fluids A 1(9), 1588–1599 (1989)

    Article  MATH  Google Scholar 

  23. Kanki, T., Iuchi, S.: Poiseuille flow and thermal creep of a rarefied gas between parallel plates. Phys. Fluids 16(5), 594–599 (1973)

    Article  MATH  Google Scholar 

  24. Chandrasekhar, S.: Radiative Transfer. Courier Corporation, USA (2013)

    MATH  Google Scholar 

  25. Barichello, L., Siewert, C.E.: A discrete-ordinates solution for a non-grey model with complete frequency redistribution. J. Quant. Spectrosc. Radiat. Transf. 62(6), 665–675 (1999)

    Article  Google Scholar 

  26. Vilhena, M., Segatto, C., Barichello, L.: A particular solution for the sn radiative transfer problems. J. Quant. Spectrosc. Radiat. Transf. 53(4), 467–469 (1995)

    Article  Google Scholar 

  27. Chien, K.-Y.: Application of the s, method to spherically symmetric radiative-transfer problems. AIAA J. 10(1), 55–59 (1972)

    Article  Google Scholar 

  28. Simch, M., Segatto, C., Vilhena, M.: An analytical solution for the sn radiative transfer equation with polarization in a slab by the ltsn method. J. Quant. Spectrosc. Radiat. Transf. 97(3), 424–435 (2006)

    Article  Google Scholar 

  29. Benoist, P., Kavenoky, A.: A new method of approximation of the boltzmann equation. Nucl. Sci. Eng. 32(2), 225–232 (1968)

    Article  Google Scholar 

  30. Siewert, C., Benoist, P.: The fn method in neutron-transport theory. Part I: Theory and applications. Nucl. Sci. Eng. 69(2), 156–160 (1979)

    Article  Google Scholar 

  31. Devaux, C., Siewert, C.: Thef n method for radiative transfer problems without azimuthal symmetry. Z. Angew. Math. Phys. ZAMP 31(5), 592–604 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  32. Garcia, R., Siewert, C.: The fn method for radiative transfer models that include polarization effects. J. Quant. Spectrosc. Radiat. Transf. 41(2), 117–145 (1989)

    Article  Google Scholar 

  33. Ganapol, B.D., Myneni, R.: The fn method for the one-angle radiative transfer equation applied to plant canopies. Remote Sens. Environ. 39(3), 213–231 (1992)

    Article  Google Scholar 

  34. Benassi, M., Garcia, R., Karp, A., Siewert, C.: A high-order spherical harmonics solution to the standard problem in radiative transfer. Astrophys. J. 280, 853–864 (1984)

    Article  Google Scholar 

  35. Siewert, C., Thomas, J., Jr.: A particular solution for the pn method in radiative transfer. J. Quant. Spectrosc. Radiat. Transf. 43(6), 433–436 (1990)

    Article  Google Scholar 

  36. Barichello, L., Siewert, C.: A discrete-ordinates solution for poiseuille flow in a plane channel. Z. Angew. Math. Phys. ZAMP 50(6), 972–981 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  37. Barichello, L., Camargo, M., Rodrigues, P., Siewert, C.: Unified solutions to classical flow problems based on the BGK model. Z. Angew. Math. Phys. ZAMP 52(3), 517–534 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  38. Siewert, C.: A concise and accurate solution to chandrasekhar’s basic problem in radiative transfer. J. Quant. Spectrosc. Radiat. Transf. 64(2), 109–130 (2000)

    Article  Google Scholar 

  39. Ganapol, B.D.: The response matrix discrete ordinates solution to the 1d radiative transfer equation. J. Quant. Spectrosc. Radiat. Transf. 154, 72–90 (2015)

    Article  Google Scholar 

  40. Ganapol, B.D.: Poiseuille channel flow by adding and doubling. In: AIP Conference Proceedings, vol. 1786, p. 070009. AIP Publishing LLC (2016)

  41. Ganapol, B.D.: 1d thermal creep channel flow in the bgk approximation by adding and doubling. Ann. Nucl. Energy 134, 441–451 (2019)

    Article  Google Scholar 

  42. Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  43. Schiassi, E., De Florio, M., D’ambrosio, A., Mortari, D., Furfaro, R.: Physics-informed neural networks and functional interpolation for data-driven parameters discovery of epidemiological compartmental models. Mathematics 9(17), 2069 (2021)

    Article  Google Scholar 

  44. Cercignani, C., Daneri, A.: Flow of a rarefied gas between two parallel plates. J. Appl. Phys. 34(12), 3509–3513 (1963)

    Article  MathSciNet  Google Scholar 

  45. Cercignani, C.: Plane Poiseuille flow according to the method of elementary solutions. J. Math. Anal. Appl. 12(2), 254–262 (1965)

    Article  MathSciNet  Google Scholar 

  46. Schiassi, E., Furfaro, R., Leake, C., De Florio, M., Johnston, H., Mortari, D.: Extreme theory of functional connections: a fast physics-informed neural network method for solving ordinary and partial differential equations. Neurocomputing 457, 334–356 (2021)

    Article  Google Scholar 

  47. Mortari, D.: The theory of connections: connecting points. Mathematics 5(4), 57 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  48. Leake, C., Mortari, D.: Deep theory of functional connections: a new method for estimating the solutions of partial differential equations. Mach. Learn. Knowl. Extr. 2(1), 37–55 (2020)

    Article  Google Scholar 

  49. Mortari, D.: Least-squares solution of linear differential equations. Mathematics 5(4), 48 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  50. Mortari, D., Johnston, H., Smith, L.: High accuracy least-squares solutions of nonlinear differential equations. J. Comput. Appl. Math. 352, 293–307 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  51. De Florio, M., Schiassi, E., D’Ambrosio, A., Mortari, D., Furfaro, R.: Theory of functional connections applied to linear odes subject to integral constraints and linear ordinary integro-differential equations. Math. Comput. Appl. 26(3), 65 (2021)

    Google Scholar 

  52. De Florio, M., Schiassi, E., Furfaro, R., Ganapol, B.D., Mostacci, D.: Solutions of chandrasekhar’ s basic problem in radiative transfer via theory of functional connections. J. Quant. Spectrosc. Radiat. Transf. 259, 107384 (2020)

    Article  Google Scholar 

  53. De Florio, M., Schiassi, E., Ganapol, B.D., Furfaro, R.: Physics-informed neural networks for rarefied-gas dynamics: thermal creep flow in the bhatnagar-gross-krook approximation. Phys. Fluids 33(4), 047110 (2021)

    Article  Google Scholar 

  54. Furfaro, R., Mortari, D.: Least-squares solution of a class of optimal space guidance problems via theory of connections. Acta Astronaut. 168, 92–103 (2019)

    Article  Google Scholar 

  55. Johnston, H., Schiassi, E., Furfaro, R., Mortari, D.: Fuel-Efficient Powered Descent Guidance on Large Planetary Bodies Via Theory of Functional Connections. arXiv preprint arXiv:2001.03572. (2020)

  56. Schiassi, E., D’Ambrosio, A., Johnston, H., Furfaro, R., Curti, F., Mortari, D.: Complete energy optimal landing on planetary bodies via theory of functional connections. Acta Astronaut. Prep. (2020)

  57. Drozd, K., Furfaro, R., Schiassi, E., Johnston, H., Mortari, D.: Energy-optimal trajectory problems in relative motion solved via theory of functional connections. Acta Astronaut. 182, 361–382 (2021)

    Article  Google Scholar 

  58. D’Ambrosio, A., Schiassi, E., Curti, F., Furfaro, R.: Pontryagin neural networks with functional interpolation for optimal intercept problems. Mathematics 9(9), 996 (2021)

    Article  Google Scholar 

  59. Namatame, A.: Connectionist learning with chebychev networks and analyses of its internal representation. In: Applications of Learning and Planning Methods, pp. 35–48. World Scientific, Singapore (1991)

    Chapter  Google Scholar 

  60. Mall, S., Chakraverty, S.: Single layer chebyshev neural network model for solving elliptic partial differential equations. Neural Process. Lett. 45(3), 825–840 (2017)

    Article  Google Scholar 

  61. Russell, R., Shampine, L.F.: A collocation method for boundary value problems. Numer. Math. 19(1), 1–28 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  62. Huang, G.-B., Zhu, Q.-Y., Siew, C.-K.: Extreme learning machine: theory and applications. Neurocomputing 70, 489–501 (2006)

    Article  Google Scholar 

  63. Liu, M., Hou, M., Wang, J., Cheng, Y.: Solving two-dimensional linear partial differential equations based on chebyshev neural network with extreme learning machine algorithm. Eng. Comput. (2020)

  64. Lagaris, I.E., Likas, A., Fotiadis, D.I.: Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 9, 987–1000 (1998)

    Article  Google Scholar 

  65. Wang, S., Teng, Y., Perdikaris, P.: Understanding and mitigating gradient flow pathologies in physics-informed neural networks. SIAM J. Sci. Comput. 43(5), A3055–A3081 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  66. Mertikopoulos, P., Papadimitriou, C., Piliouras, G.: Cycles in adversarial regularized learning. In: Proceedings of the Twenty-Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 2703–2717. SIAM (2018)

  67. Balduzzi, D., Racaniere, S., Martens, J., Foerster, J., Tuyls, K., Graepel, T.: The mechanics of n-player differentiable games. In: International Conference on Machine Learning, pp. 354–363. PMLR (2018)

  68. Siewert, C., Garcia, R., Grandjean, P.: A concise and accurate solution for Poiseuille flow in a plane channel. J. Math. Phys. 21(12), 2760–2763 (1980)

    Article  MathSciNet  MATH  Google Scholar 

  69. Sharipov, F.: Application of the cercignani-lampis scattering kernel to calculations of rarefied gas flows. I. Plane flow between two parallel plates. Eur. J. Mech.-B/Fluids 21(1), 113–123 (2002)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Systems and Industrial Engineering, The University of Arizona, Tucson, AZ, 85721-0020, USA

    Mario De Florio, Enrico Schiassi & Roberto Furfaro

  2. Department of Aerospace and Mechanical Engineering, The University of Arizona, Tucson, AZ, 85721-0020, USA

    Barry D. Ganapol & Roberto Furfaro

Authors
  1. Mario De Florio
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Enrico Schiassi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Barry D. Ganapol
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Roberto Furfaro
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Roberto Furfaro.

Ethics declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

De Florio, M., Schiassi, E., Ganapol, B.D. et al. Physics-Informed Neural Networks for rarefied-gas dynamics: Poiseuille flow in the BGK approximation. Z. Angew. Math. Phys. 73, 126 (2022). https://doi.org/10.1007/s00033-022-01767-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-022-01767-z

Keywords

Mathematics Subject Classification

Search

Navigation