Homogenization of Winkler–Steklov spectral conditions in three-dimensional linear elasticity

Abstract

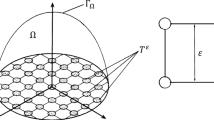
We consider a homogenization Winkler–Steklov spectral problem that consists of the elasticity equations for a three-dimensional homogeneous anisotropic elastic body which has a plane part of the surface subject to alternating boundary conditions on small regions periodically placed along the plane. These conditions are of the Dirichlet type and of the Winkler–Steklov type, the latter containing the spectral parameter. The rest of the boundary of the body is fixed, and the period and size of the regions, where the spectral parameter arises, are of order $\varepsilon$. For fixed $\varepsilon$, the problem has a discrete spectrum, and we address the asymptotic behavior of the eigenvalues $\{\beta _k^\varepsilon \}_{k=1}^{\infty }$ as $\varepsilon \rightarrow 0$. We show that $\beta _k^\varepsilon =O(\varepsilon ^{-1})$ for each fixed k, and we observe a common limit point for all the rescaled eigenvalues $\varepsilon \beta _k^\varepsilon$ while we make it evident that, although the periodicity of the structure only affects the boundary conditions, a band-gap structure of the spectrum is inherited asymptotically. Also, we provide the asymptotic behavior for certain “groups” of eigenmodes.