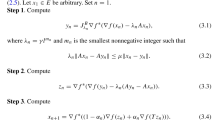Skip to main content
SpringerLink
Log in

Convergence of Two Simple Methods for Solving Monotone Inclusion Problems in Reflexive Banach Spaces

  • Published:
Results in Mathematics Aims and scope Submit manuscript

Abstract

We propose two very simple methods, the first one with constant step sizes and the second one with self-adaptive step sizes, for finding a zero of the sum of two monotone operators in real reflexive Banach spaces. Our methods require only one evaluation of the single-valued operator at each iteration. Weak convergence results are obtained when the set-valued operator is maximal monotone and the single-valued operator is Lipschitz continuous, and strong convergence results are obtained when either one of these two operators is required, in addition, to be strongly monotone. We also obtain the rate of convergence of our proposed methods in real reflexive Banach spaces. Finally, we apply our results to solving generalized Nash equilibrium problems for gas markets.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data Availability

Not applicable.

References

  1. Attouch, H., Cabot, A.: Convergence of a relaxed inertial forward-backward algorithm for structured monotone inclusions. Appl. Math. Optim. 80, 547–598 (2019)

    Article  MathSciNet  Google Scholar 

  2. Barbu, V.: Nonlinear Differential Equations of Monotone Types Nonlinear Differential in Banach Spaces. Springer, New York (2010)

    Book  Google Scholar 

  3. Bauschke, H.H., Matoušková, E., Reich, S.: Projection and proximal point methods: convergence results and counterexamples. Nonlinear Anal. 56, 715–738 (2004)

    Article  MathSciNet  Google Scholar 

  4. Bauschke, H.H., Wang, X., Yao, L.: General resolvents for monotone operators: characterization and extension. In: Censor, Y., Jiang, M., Wang, G. (eds.) Biomedical Mathematics: Promising Directions in Imagine, Therapy Planning and Inverse Problem (Huangguoshu 2008), pp. 57–74. Medical Physics Plublishing, Madison, WI, USA (2010)

    Google Scholar 

  5. Bertsekas, D.: Convex analysis and optimization contributors. Athena Scientific, Angelia Nedic and Asuman E. Ozdaglar. Belmont (2003)

    Google Scholar 

  6. Bregman, L.M.: The relaxation method for finding common points of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. Math. Phys. 7, 200–217 (1967)

    Article  MathSciNet  Google Scholar 

  7. Bregman, L.M., Censor, Y., Reich, S.: Dykstra’s algorithm as the nonlinear extension of Bregman’s optimization method. J. Convex Anal. 6, 319–333 (1999)

    MathSciNet  MATH  Google Scholar 

  8. Bruck, R.E., Reich, S.: Nonexpansive projections and resolvents of accretive operators in Banach spaces. Houston J. Math. 3, 459–470 (1977)

    MathSciNet  MATH  Google Scholar 

  9. Butnariu, D., Iusem, A.N.: Totally convex functions for fixed points computational and infinite dimensional optimization. Kluwer Academic, Dordrecht (2000)

    Book  Google Scholar 

  10. Chang, Ss., Yao, J.C., Wen, C.F., Qin, L.J.: Shrinking projection method for solving inclusion problem and fixed point problem in reflexive Banach spaces. Optimization (2020). https://doi.org/10.1080/02331934.2020.1763988

    Article  MATH  Google Scholar 

  11. Chidume, C.E.: Geometric properties of Banach spaces and nonlinear iterations, Springer Verlag Series, Lecture Notes in Mathematics, ISBN 978-1-84882-189-7, (2009)

  12. Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul. 4, 1168–1200 (2005)

    Article  MathSciNet  Google Scholar 

  13. Grimm, V., Hintermüller, M., Huber, O., Schewe, L., Schmidt, M., Zöttl, G.: A PDE-constraints generalized Nash equilibrium approach for modeling gas markets with transport, (2021), https://opus4.kobv.de/opus4-trr154/frontdoor/index/index/docId/458

  14. Hieu, D.V., Cholamjiak, P.: Modified extragradient method with Bregman distance for variational inequalities. Appl. Anal. (2020). https://doi.org/10.1080/00036811.2020.1757078

    Article  MATH  Google Scholar 

  15. Huang, Y.Y., Jeng, J.C., Kuo, T.Y., et al.: Fixed point and weak convergence theorems for point-dependent \(\lambda \)-hybrid mappings in Banach spaces. Fixed Point Theory Appl. 2011, 105 (2011)

    Article  MathSciNet  Google Scholar 

  16. Jolaoso, L.O., Shehu, Y.: Single Bregman projection method for solving variational inequalities in reflexive Banach spaces. Appl. Anal. (2021). https://doi.org/10.1080/00036811.2020.1869947

    Article  Google Scholar 

  17. Lions, P.L., Mercier, B.: Splitting algorithms for the sum of two nonlinear operators. SIAM J. Numer. Anal. 16, 964–979 (1979)

    Article  MathSciNet  Google Scholar 

  18. Liu, H., Yang, J.: Weak convergence of iterative methods for solving quasimonotone variational inequalities. Comput. Optim. Appl. 77(2), 491–508 (2020)

    Article  MathSciNet  Google Scholar 

  19. Malitsky, Y., Tam, M.K.: A forward-backward splitting method for monotone inclusions without cocoercivity. SIAM J. Optim. 30, 1451–1472 (2020)

    Article  MathSciNet  Google Scholar 

  20. Martin-Marquez, V., Reich, S., Sabach, S.: Bregman strongly nonexpansive operators in reflexive Banach spaces. J. Math. Anal. Appl. 400, 597–614 (2013)

    Article  MathSciNet  Google Scholar 

  21. Martinet, B.: Régularisation d’Inéquations Variationnelles par Approximations Successives. Rev. Franćaise d’Inform. et de Rech. Opérationnelle 3, 154–158 (1970)

    MATH  Google Scholar 

  22. Nesterov, Y.: Introductory lectures on convex optimization, A basic course, pp. 63–64. Kluwer Academic, Berlin (2004)

    Book  Google Scholar 

  23. Nevanlinna, O., Reich, S.: Strong convergence of contraction semigroups and of iterative methods for accretive operators in Banach spaces. Israel J. Math. 32, 44–58 (1979)

    Article  MathSciNet  Google Scholar 

  24. Ogbuisi, F.U.: On common solution of a monotone variational inclusion for two mappings and a fixed point problem. U. Politeh. Buch. Ser. A 81, 111–122 (2019)

    MathSciNet  Google Scholar 

  25. Ogbuisi, F.U., Izuchukwu, C.: Approximating a zero of sum of two monotone operators which solves a fixed point problem in reflexive Banach spaces. Numer. Funct. Anal. Optim. 41, 322–343 (2020)

    Article  MathSciNet  Google Scholar 

  26. Okeke, C.C., Izuchukwu, C.: Strong convergence theorem for split feasibility problems and variational inclusion problems in real Banach spaces. Rend. Circ. Mat. Palermo 70, 457–480 (2021)

    Article  MathSciNet  Google Scholar 

  27. Orouji, B., Soori, E., O’Regan, D., Agarwal, R.P.: A strong convergence theorem for a finite family of Bregman demimetric mappings in a Banach space under a new shrinking projection method, J. Funct. Spaces, Volume 2021, Article ID 9551162, p. 11 (2021). https://doi.org/10.1155/2021/9551162

  28. Passty, G.B.: Ergodic convergence to a zero of the sum of monotone operators in Hilbert space. J. Math. Anal. Appl. 72, 383–390 (1979)

    Article  MathSciNet  Google Scholar 

  29. Reem, D., Reich, S.: Solutions to inexact resolvent inclusion problems with applications to nonlinear analysis and optimization. Rend. Circ. Mat. Palermo 67, 337–371 (2018)

    Article  MathSciNet  Google Scholar 

  30. Riech, S., Sabach, S.: Two strong convergence theorems for a proximal method in reflexive Banach spaces. Numer. Funct. Anal. Optim. 31, 24–44 (2010)

    MathSciNet  Google Scholar 

  31. Reich, S., Sabach, S.: A strong convergence theorem for a proximal-type algorithm in reflexive Banach spaces. J. Nonlinear Convex Anal. 10, 471–485 (2009)

    MathSciNet  MATH  Google Scholar 

  32. Rockafellar, R.T.: Monotone operators and the proximal point algorithm. SIAM J. Control. Optim. 14, 877–898 (1976)

    Article  MathSciNet  Google Scholar 

  33. Shehu, Y.: Single projection algorithm for variational inequalities in Banach spaces with application to contact problem. Acta. Math. Sci. 40, 1045–1063 (2020)

    Article  MathSciNet  Google Scholar 

  34. Shehu, Y.: Convergence results of forward-backward algorithms for sum of monotone operators in Banach spaces. Results Math. 74, 1–24 (2019). (Article Number 138)

    Article  MathSciNet  Google Scholar 

  35. Sunthrayuth, P., Pholasa, N., Cholamjiak, P.: Mann-type algorithms for solving themonotone inclusion problem and the fixed point problem in reflexive Banach spaces. Ricerche mat. (2021). https://doi.org/10.1007/s11587-021-00596-y

    Article  Google Scholar 

  36. Tang, Y., Promkam, R., Cholamjiak, P., Sunthrayuth, P.: Convergence results of iterative algorithms for the sum of two monotone operators in reflexive Banach spaces. Appl. Math. (2021). https://doi.org/10.21136/AM.2021.0108-20

    Article  MATH  Google Scholar 

  37. Tseng, P.: A modified forward-backward splitting method for maximal monotone mappings. SIAM J. Control. Optim. 38, 431–446 (2000)

    Article  MathSciNet  Google Scholar 

  38. Tuyen, T.M., Promkam, R., Sunthrayuth, P.: Strong convergence of a generalized forward-backward splitting method in reflexive Banach spaces. Optimization (2020). https://doi.org/10.1080/02331934.2020

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The second author was partially supported by the Israel Science Foundation (Grant 820/17), by the Fund for the Promotion of Research at the Technion and by the Technion General Research Fund.

Author information

Authors and Affiliations

  1. Department of Mathematics, The Technion – Israel Institute of Technology, 32000, Haifa, Israel

    Chinedu Izuchukwu & Simeon Reich

  2. College of Mathematics and Computer Science, Zhejiang Normal University, Jinhua, 321004, People’s Republic of China

    Yekini Shehu

Authors
  1. Chinedu Izuchukwu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Simeon Reich
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yekini Shehu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All the authors contributed to this paper.

Corresponding author

Correspondence to Yekini Shehu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Code availability

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Izuchukwu, C., Reich, S. & Shehu, Y. Convergence of Two Simple Methods for Solving Monotone Inclusion Problems in Reflexive Banach Spaces. Results Math 77, 143 (2022). https://doi.org/10.1007/s00025-022-01694-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00025-022-01694-5

Keywords

Mathematics Subject Classification

Search

Navigation