1 Introduction

To better illustrate the motivation for this study, let us start with a question. Why do we need a gravity tide model for the Lake Nasser region? Tidal observations are important both for the accurate determination of the tidal correction of precise geodetic measurements, and for assessing the structure and elastic properties of the Earth on a global scale. It is generally recognised that an important step in processing gravimetric data, both static and dynamic, is to make accurate tidal corrections. Reliable tidal corrections are based on accurate tidal gravimetric factors. Therefore, the main objective we want to pursue with this research is to recover a first reliable gravity tidal model for the Lake Nasser region. This is a very interesting area from a geophysical point of view, since it is affected by active tectonics controlled by several seismogenic faults, as evidenced by historical and current seismicity (Dahy, 2012). Therefore, studying the effect of Lake Nasser level variations on crustal deformation and related gravity changes becomes a topic of great general interest. We believe that precise geodetic observations, for future geophysical studies in the region, should benefit from such a model.

1.1 Lake Nasser and Its Seismotectonic Relevance

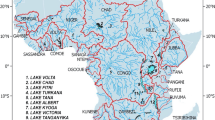
Hydroelectric power generation, flood control and irrigation have globally led to the creation of huge artificial water reservoirs, of which Lake Nasser is one of the largest worldwide. It has formed after the creation of the Aswan High Dam (AHD) in 1971 on the River Nile. The lake is located in a desert region, namely in a very hot and dry climate with an annual evaporation rate of 2.1–2.6 m/year and negligible precipitations (Ebaid & Ismail, 2010; Elsawwaf et al., 2010). It extends from the Arabian/Eastern Desert, east of the Nile, to the low sand dunes and depressions of the Western Desert (Fig. 1). The dam was built to provide hydroelectric power to the cities (2100 MW) and to boost the agricultural economy and food supplies in Egypt through a constant supply of water for irrigation (55.5 km3/year) and fishing industry. The lake is about 500 km long, 67% of which sit in Egypt and 33% in Sudan. Lake Nasser plays a vital role in Egypt's economy and life as it stores and regulates water from the Nile, being the main source of fresh water for about 85% of its population. The operating trends of the Nasser reservoir aim to guarantee an adequate water supply and the safety of the Aswan High Dam. At the onset of the hydrological year (“water year”), early August, the water level is maintained at 175 m above sea level (asl) to meet the high and low flow requirement. When the upstream water level reaches between 178 and 183 m, excess water is deviated to the Toshka depression and the emergency spillways on the west bank of the Nile (Mobasher, 2010). The water level fluctuates between roughly 168 m and 178 m; the seasonal cycle (annual) can be divided into four different periods of inflow, stability, discharge, and back to stability. The maximum retention at nearly 180 m asl is attained in November and, subsequently, reservoir levels decrease from January to July when the water is released (Muala et al., 2014).

Fig. 1
figure 1

Lake Nasser region (Google Earth image): location of the two recording gravity stations of the Imhotep Project. Main faults are marked (red line = Kalabsha faults; blue lines other active faults of the region). Fault positions are retrieved from Nubian Project (https://www.esrs.wmich.edu/arcgis/rest/services/Nubian_project/MapServer/generateKml) and North Africa for the Global Earthquake Model Foundation's Global Active Faults compilation compiled by R. Styron (https://doi.org/10.13117/n-africa-active-faults); the reference point (red spot) for the available satellite altimetry used to compare with gravity residuals is indicated too

Full size image

The northern sector of the Lake is known to be seismically active since the occurrence of a strong earthquake in November 1981 (ML = 5.6), about 60 km southwest of Aswan High Dam. Detailed geological and geophysical investigations in the area confirm the existence of several active faults to the southwest of the Aswan High Dam (e.g. the Kalabsha fault). Many authors (e.g. Dahy, 2012; Hamimi & Hagag, 2017) believe that the seismic activity in this area could be related either to tectonic activities along these active faults and/or to reservoir-triggered seismicity (RTS) due to Lake Nasser. Globally there are hundreds of sites where RTS is reported to have occurred (Gupta, 2021). This is why studying the dynamics of the lake and its relationship on induced ground deformations is of paramount importance. The reservoir itself is not expected to produce earthquakes, but it might trigger the release of pre-stored stresses in the earth's crust along faults crossing the area. Actually, the RTS is the dynamic response of the rock volumes to changes in water level that alter the elastic equilibrium in the surrounding rock volumes. The ground water changes driven by the lake level changes plays a pivotal role in this process. It may result from changes in pore stress or pressure, in volume, loading or unloading cycles in the rock mass and combinations of these causes. Pore pressure may increase due to a decrease in pore volume caused by compaction under the weight of the reservoir and/or due to the diffusion of reservoir water through the permeable rock beneath the reservoir. Permeability of the rocks controls the rate of flow, so this effect might be not instantaneous. The increase in pore pressure takes longer depending on the distance from the reservoir. It can take years for pore pressure to increase at depths of kilometres beneath a reservoir. There is evidence that both water loading and changes in pore-fluid deformation played an important role in triggering the shallower activity, while pore-fluid pressure is the main factor triggering the deeper activity (Woodward-Clyde Consultants, 1985; Abu Elenean, 2007).

The variation of the mass of the water of the reservoir affects both the potential field and strain either by loading or by changing the ground water level. To detect these signals an intense program of geodetic, seismological and hydrologic monitoring is still ongoing since early 2000s.

1.2 Previous Gravity Studies on the Area

Time-lapse gravity surveys were performed and repeated at different times along the sites of the regional network to study the temporal gravity variations around the northern sector of Lake Nasser. Gravity variations on the order of tens of μGal were observed in the period November 2001–November 2002 (Zahran, 2005). According to that author, the temporal variations in gravity largely obey changes in the lake's water level. This could indicate a significant redistribution of mass around the active faults intersecting the area, which may have some interaction with seismic activity. Seasonal variations in the level of Lake Nasser are likely to change the stress regime in the area and, therefore, changes in the gravitational field and crustal deformations are reasonably expected (Saleh et al., 2018; Telesca et al., 2012, 2017); see also Johnson et al., 2017 for loading effects on Californian faults.

In the framework of a project aimed at monitoring the crustal deformation and its relation to the seismological activities in Cairo region, 1 year of tidal gravity observations were collected at Helwan (at about 25 km south of Cairo city) using the same instrument (LCR_ET16) as used for this study. Gravity records were carried out to determine the real response of the Earth to the tidal force and in consequence a precise correction for both gravity and GPS observations in Cairo region (Zahran et al., 2004). Unfortunately, these analyses led to large gravity residuals, with significant energy in both diurnal and semidiurnal bands and high standard deviations, which the authors deem to be due to the high noise of the station and the low performance of the feedback of the instrument. Furthermore, comparison of the observed and theoretical parameters indicated higher discrepancies of the phases than the gravimetric factors mainly in the semidiurnal band. Gravimetric records have already been acquired at the Aswan tide station in the past. In fact, some records collected during about 2 years (from December 2002 to November 2004) at this site were used by Hassan et al., (2010a, 2010b) to study gravity variations induced by changes in the level of Lake Nasser. Gravity records were acquired with the same gravimeter (LCR_D-128) that was subsequently installed at Abu Simbel for this study. The outcomes of tidal analyses (Hassan et al., 2010a) were that most of the tidal waves in the diurnal group had a gravimetric factor close to one and much smaller than the global gravimetric factor, while most of the gravimetric factors in the semi-diurnal band were close to the global value (1.16). Almost all wave groups had phase shifts close to zero. The highest standard deviations were found for waves K1 and S2, leading the authors to invoke an effect of air pressure and solar variation during the day, which is expected in tropical areas such as Aswan or alternatively attributed to a problem in the instrumental chain, i.e. the quartz clock drift of the Data AcQuisition (DAQ) system. Even more interesting were the results in terms of gravity residuals, which showed noise levels in the diurnal and semidiurnal at 16 nm/s2 and 9 nm/s2 respectively. This clearly proves that the tidal waves were not completely separated. All these outcomes claim for a need of a more accurate tidal model for the region.

Two methods were used by Hassan et al. (2010b) to evaluate the gravity variations in the tidal records due to variations of water level at Lake Nasser: (a) block analysis; (b) correlation analysis between water levels and gravity residuals. As for the first method, gravity records were divided into blocks, each block representing an epoch of a certain water level in the lake, namely decrease, stability, and increase of water level. Changes up to 4% in amplitude factors, and 0.5° in phase shifts were observed in the tidal parameters for different blocks with different water levels. The observed changes were explained in terms of different loading conditions inducing pore pressure changes, and, thus, modifications of overall elasticity of the crustal medium. Notwithstanding a weak correlation emerged between water level variation and residual gravity, Hassan et al. (2010b) deduced that the residual gravity follows water level variation with a certain time delay. They interpreted the recognized time shift as a consequence of the permeability of the rocks and migrating water masses.

The LCR_D-128 was also used for about 1 year from February 2008 to February 2009 in Hurgada (Red Sea) to characterise the crustal response to tidal force and to determine a reliable tidal model for the region (Hassan et al., 2010c). The Red Sea is classified among the areas of highest seismic potential in Egypt and is of primary geodynamic interest being a rift that represents the locus of sea floor spreading and a divergent environment between the two major African and Arabian plates (El-Isa, 2015).

2 Principles and Algorithms of Gravity Tidal Analyses

2.1 Principles of Gravity Tidal Analyses

The tides on the planet Earth are due to the differential gravitational forces caused principally by the Sun and the Moon and subordinately by other bodies of the solar system. This differential acceleration also combines with the intrinsic rotation of the Earth. A number of reviews on Earth tides are available, e.g. the collection of articles by Wilhelm et al. (1997) provides an adequate review of the state of the art on the subject.

The Earth deforms under the tidal stress, so the tidal potential on a rigid Earth has to be considered only a first-order approximation. For most geophysical purposes the Earth can be considered as SNREI (spherical, non-rotating, elastic, isotropic). Three dimensionless elastic parameters, called Love numbers hn, kn, after A.E.H. Love, and the Shida number ln, are routinely used to describe the deformation of the Earth under tidal stress (Love, 1911), where n stands for the degree of the harmonic development of the tide-generating potential; indeed, the Shida number can be ignored for surface gravity. It is common to use the delta parameter or gravimetric factor (δn) to characterise gravity variations due to tidal interaction. The relation between the gravimetric factor (δn) and the Love numbers is given for each degree n by:

$${\delta }_{n}=1+\frac{2}{n}{h}_{n}-\frac{n+1}{n}{k}_{n}$$
(1)

Physically, δn can be defined as the ratio of the vertical component of body tide measured by a gravimeter divided by the gradient of external tidal potential along the perpendicular to the reference ellipsoid. For a standard modern Earth model (PREM), assuming n = 2, it follows δ2 = 1.16 with h2 = 0.6032, k2 = 0.2980. For more realistic Earth models the effects of rotation, ellipticity, inelasticity, and anisotropy, have to be accounted for. Most recent tidal models are the Hydrostatic, elastic Earth model (DDW-H), the Non-Hydrostatic, inelastic Earth model (DDW-NHi) (Dehant et al., 1999) and the Non-Hydrostatic, inelastic Earth model (WDZ-NHi) (Dehant & Zschau, 1989; Wahr & Bergen, 1986). Inelasticity causes a small tidal phase lag (time delay) due to frictional deformation in the mantle so δ becomes complex. Therefore, it is customary to also introduce a phase lag φn that gives the delay of the tidal response with respect to the phase of the external tidal potential. Moreover, in a dispersive medium the Love numbers become frequency dependent. Consequently, the Earth has a different gravimetric response to each tidal constituent.

In addition to the solid Earth or body tides, the fluid oceans react under the tidal potential that changes the height of the ocean column. Ocean tidal loading (OTL) acts on the crust and give vertical deformation, and a set of load Love numbers for each degree exists that are similar to the tidal Love numbers defined above. Some programs and services are available online (Bos & Scherneck, 2021) implementing models to compute the geophysical effects due to the OTL. Most of the programs and services have been intercompared and use satellite altimeter data from space missions like Topex/Poseidon for precise ocean models. As OTL is generally less than 10% of the solid Earth tide, it is enough to determine the loading for a very small subset of all possible ocean tidal waves. In most OTL models, amplitude and phase effects are calculated only for 9 main waves which, following Darwin's notation, are: 4 diurnal (O1, K1, P1, Q1), 4 at semidiurnal periods (K2, M2, N2, S2), and one fortnightly (Mf).

Aimed to determine the global response of the Earth to the tidal forcing, a number of Earth tide observations have been collected at many stations worldwide under the umbrella of the IGETS International Geodynamics and Earth Tide Service (http://igets.u-strasbg.fr/).

Accurate knowledge of Earth’s body tides is crucial for correcting geodetic observations such as positioning measurements, satellite gravity surveys, and terrestrial, aerial, and submarine gravity observations with microGal or even better nanoGal precision as well as to investigate the structure and elastic properties of the Earth at global scale. Retrieving the three-dimensional elastic properties of the Earth from tidal observations is a challenging task, it requires very high sensitivity and accuracy of the instruments, local perturbation correction and data analysis. Nowadays Earth tides can be observed mainly by gravimeters, tilt- and strainmeters. However, gravity tides can be measured with very high signal to noise ratio with superconducting and spring gravimeters equipped with electrostatic feedbacks (Rosat et al., 2015; Zürn, 1997). Actually, it is worth bearing in mind that, in the gravity tide, the Earth's elastic properties are contained in only 16% of the signal. Most of the gravity signal (84%) can be calculated very accurately from catalogues, which drastically improves the apparent signal-to-noise ratio. Unlike the gravitational tide, which is very weakly biased by local, regional and large-scale anomalies in the Earth's spherical symmetry, the tidal field measured by tilt and strainmeters is heavily biased by local heterogeneities, such as cavity effects, making such instruments unsuitable for measuring the global and regional response of the Earth (Riccardi et al., 2016). Thus, gravimetric observations are considered the most reliable tool for obtaining the Earth's response to tidal forcing.

According to Wenzel (1997), the response of the Earth to the tides in the frequency domain (f) can be seen as a transfer function (H(f)), so that the observed tidal spectrum (Y(f)) results from the product of the theoretical tidal spectrum (X(f)) with the transfer function:

$$Y\left(f\right)=H\left(f\right)\cdot X\left(f\right)$$
(2)

Since the tidal response of the Earth is suitably represented by the delta factors (δ) and phase leads (φ) for specific tidal frequencies of the tidal potential, the main goal of each tidal analyses is to retrieve accurate tidal parameters. Tidal analyses are usually performed on continuous records collected by permanent gravity stations equipped with spring or superconducting gravimeters. According to Rayleigh's criterion and Munk and Hasselmann (1964), the number of tidal groups that can be separated depends on the data length and the signal-to-noise ratio. The availability of very sensitive superconducting gravimeters (Hinderer et al., 2015) has driven extensive computations of the tidal potential and its harmonic decomposition to achieve more precision to target elusive geophysical signals from the Earth interior. The latest and most accurate expansions of the tidal potential are those due to Hartmann and Wenzel (1995a; 1995b) HW95, counting nearly 13,000 harmonics, and Kudryavtsev (2004) with 27,000 constituents.

2.2 Algorithms and Software Systems for Tidal Analyses

Different programs for tidal analysis are available such as ANALYZE (ETERNA 3.40) program (Wenzel, 1996), the VAV06 software (Venedikov et al., 2005), BAYTAP-G (Tamura et al., 1991) and more recently the ET34-ANA-X version of ETERNA (Schüller, 2020).

For this study, we used ET34-ANA-V80 (Schüller, 2020). This is a freely available program for Earth and ocean tide parameter estimation and signal prediction. Compared to former Eterna 3.40, ET34-ANA-X reflects many important enhancements in order to more accurately analyse and retrieve related information about the Earth concealed in tidal observations. An exhaustive description of the new features, released as system variant ET34-x-v80-gnusim, are provided in the webpage (http://ggp.bkg.bund.de/eterna/). The core program is based on a method developed by Chojnicki (1973) and improved by Schüller (1976, 2020) and Wenzel (1996). A least squares adjustment is used to estimate the tidal parameters, the meteorological and hydrological regression parameters, the pole tide regression parameters and the Tschebyscheff-polynomial bias parameters for drift determination. Several Earth tide data (gravity, tide gauge, strain, tilt and displacement) can be analysed jointly with meteorological and hydrological data. In order to calculate the theoretical tidal signal, the user can select the suitable tidal potential catalogue among ten catalogues including the very accurate one from Hartmann and Wenzel (1995a, 1995b). It is possible to determine the range of up to a hundred or so tidal wave groups; details on the model used for least square adjustment can be found in Schüller (2020).

3 The Recording Gravity Stations and Datasets

As part of the French-Egyptian Imhotep project, which started in 2015 and is still ongoing, two spring gravimeters were installed in the area of Lake Nasser (Egypt). The two permanent gravity stations are located at Aswan, on the northern edge of the lake, and at Abu Simbel in the south, respectively (Fig. 1 and Table 1). The Aswan station is equipped with the LaCoste & Romberg ET16 (LCR_ET16) terrestrial tidal gravimeter supplied by the University of Darmstadt (Germany). In the same site the LCR-D128 gravimeter, equipped with a maximum voltage retroaction (MVR) electrostatic feedback (van Ruymbeke, 1991), has operated along 2 years (Hassan et al., 2010a), then it was moved to Abu Simbel in 2019. The station is set in the basement of the main building of the Seismological Centre of the High Dam Authority at Sahari (Aswan). The LCR_ET16 is an Earth tide (ET) gravimeter, specially designed in the 1970s by LaCoste & Romberg (LCR) manufacturer to meet the requirements of high precision recording of time variable gravity due to tides. With respect to a standard land survey gravity meter an ET has a larger case because of a controlled double oven able to ensure a very stable internal temperature. This should result in substantial improvements in noise reduction and in achieving a lower and linear drift. More than 10 years ago, Microg-Lacoste Inc. started the production of a new generation of portable Earth tide gravimeter (PET). Since then, the name changed to gPhone and more recently gPhoneX (Microg-LaCoste, 2013). The gPhone is essentially an LCR, model G meter, but with significant upgrades: the size is smaller than the former PET notwithstanding the double oven. The feedback system is the Aliod beam nulling system allowing more precise digital measurements at the level of 1 nm/s2 (0.1 μGal). Moreover, the data logger can be accurately synchronized through a pps (pulse-per-second) clock device and a GPS clock antenna.

Table 1 Permanent gravity stations: location, equipment and data availability for this study
Full size table

The great care given to the pressure seals makes it almost insensitive to humidity and buoyancy effects, which would allow a coherent response of the meter to the atmospheric pressure fluctuations (Riccardi et al., 2011). Indeed, the pressure sealing is a feature that degrades over the years; this is the case for LCR_ET16 used for this study.

The original mechanical feedback of the LCR_ET16 meter was replaced with a home-made electrostatic one following the Weber-Larson principle (Weber & Larson, 1966). This was due to the fact that the mechanical system suffered from a severe backlash amounting to nearly 3 μGal leading to incoherent phase lag for both diurnal and semidiurnal tidal groups (Gerstenecker & Schüller, 1983). Actually, electrostatic feedback suffers from the well-known non-linearity when the beam is forced to operate at a position different from the geometrical center between the outer capacitor plates. Nonlinearity could be strongly reduced (< 0.2%) by carefully adjusting the outer plates, but this task is quite challenging and should be done by skilled operators (W. Zürn Personal communication). This difficulty is reported even by Block and Moore (1966) and Weber and Larson (1966), who discuss methods for applying electrostatic feedback to these instruments. In these methods the relationship between feedback voltage and gravitational force is usually nonlinear and can be linearized only with some difficulty using a mechanical adjustment of the feedback capacitor plates (Moore & Farrell, 1970).

Anyway, after the home-made feedback conversion the performances of LCR_ET-16 has been tested during different intercomparisons (e.g. Xu et al., 1989).

The instrument is installed on a pillar connected to the bedrock in a double wall well-isolated building. Thermic isolation is further improved by putting the gravimeter in a small well isolated wooden shelter. Continuous temperature observation shows that the temperature stability around the instrument is better than 1 °C per day.

The Abu Simbel station is located in a desert area, housed in a purpose-built concrete shelter within the compound of the Geophysical Observatory (Fig. 1 and Table 1). At the start of the Imhotep project, the station was instrumented with the LCR_ET18 terrestrial tidal gravimeter, but after a few months of good work, its electrostatic feedback, installed by Larson (1968), experienced some failures. Then it was replaced with the LaCoste & Romberg model D terrestrial gravimeter (LCR_D-218) belonging to the National Research Institute of Astronomy and Geophysics (NRIAG). In 2002 the LCR_D-218 has been calibrated on a calibration line by comparing the gravity difference between two gravity sites, 15 km apart, with known absolute Δg values (42 mGal), located close to the Aswan tidal station (Hassan et al., 2010a). However, the complete scaling factors (from arbitrary to gravity units) have never been published.

At the two stations, in addition to gravity, barometric variations are also measured by means of the dedicated sensors (Schlumberger, DUX). In both stations the gravity and barometric output signals are digitally recorded using data acquisition boards USB-DUX Sigma, with 24-bits resolution over 16 channels, 24-bits digital I/O, 4 D/A outputs and electrical isolation of all analogic channels.

The data available for the purpose of this study cover the following time intervals: Aswan: 1 May 2018 to 8 April 2021; Abu Simbel: (a) 5 March 2019 to 8 April 2021; (b) 20 October 2021–31 January 2022 (Table 1); the true useful record lengths is given in Table 2.

Table 2 Tidal parameters (δ and φ) and their statistical quality (RMS, Error) for the main tidal waves retrieved from the tidal analyses; theoretical gravimetric factors (δtheo) according to (DDW-NHi) Earth model are listed too
Full size table

4 Data Analysis

4.1 Data Pre-processing

Gravity records collected in Aswan and Abu Simbel are shown in Figs. 2, 3. To take full advantage of continuous gravity records for geophysical purposes, sampled at high rate (1 Hz), some tares (spikes, steps and gaps) have to be cleaned first from the signal. An automatic method, the so called “Slew method” has been proposed by Crossley et al. (1993). The program TSOFT (Van Camp & Vauterin, 2005) provides very useful tools capable of performing the above steps of the data pre-processing including data interpolation, filtering, decimation and spectral analyses.

Fig. 2
figure 2

Gravity records and pre-processing at Aswan station: raw feedback (FB) voltage output (a); cleaned FB voltage with drift (red curve) (b); high-pass filtered feedback voltage (c); theoretical tide (DDW-H) in nm s−2 (d); gravity effect in nm s−2 due to Ocean Tide loading (OTL) model FES2014b with polar motion contribution (blue curve) (e); nominal gravity effect in nm s−2 due to atmospheric pressure changes (f) (see main text for details and references)

Full size image
Fig. 3
figure 3

Gravity records and pre-processing at Abu Simbel station: raw feedback (FB) voltage (a); cleaned FB voltage with drift (red curve) (b); high-pass filtered feedback voltage (c); theoretical tide (DDW-H) in nm s−2 (d); gravity effect in nm s−2 due to Ocean Tide loading (OTL) model FES2014b with polar motion contribution(blue curve) (e); nominal gravity effect in nm s−2 due to the atmospheric pressure changes (f); gravity residuals in nm s−2 (g) (see main text for details and references)

Full size image

The raw data are originally collected at 1 Hz sampling rate, then for the pre-processing samples are decimated from 1 to 60 s using a digital low-pass filter with a cut-off frequency of 0.00833 Hz and window half-length 504 samples. Finally, to be used for tidal analyses, they are further decimated from 60 to 3600 s (1 h) by using a least-square low-pass filtering with cut-off frequency of 12 cycle per day (cpd) and window half-length 480 samples (8 min). Cleaned and uncalibrated data are shown in the Figs. 2b and 3b.

Since we aim to retrieve the scale factors to convert the collected signal from volts into gravity units (nm/s2) from correlation with a synthetic reference tide, records have been high-pass filtered with a FFT filtering with a cut-off frequency fixed at 0.1 cpd and bandwidth 0.01 cpd which has a suitable pass-band in the main tidal frequencies (nearly 1 and 2 cpd). In principle, this approach might be considered safe for keeping the spectral energy in the main tidal bands, but it is quite unsafe and unsuitable to study the long-period gravity changes that might be due to the hydrology or equivalently to the Nasser Lake level changes. This point will be discussed in the following Sect. 5.2 (Gravity Residuals and Lake Nasser Level changes). The high-pass filtered data (Figs. 2c, 3c) have been used for the calibration.

4.2 Calibrations

Accurate calibration of relative gravimeters is essential to capture elusive, low-amplitude gravity signals produced by endogenous and exogenous processes. In fact, recent technological advances in gravity sensors have made addressable a number of geophysical phenomena involving underground mass redistribution and/or Earth's changing shape, (e.g. Earth tides, volcano and groundwater monitoring, sea level and reservoir changes, Earth's core and wobble modes, ocean and atmospheric loading, polar motion, free-core and inner-core nutations) (e. g. Crossley et al., 2013; Hinderer et al., 2015; Riccardi et al., 2008). The magnitude of the gravity changes induced by these phenomena can be very small, on the order of 10–8 ÷ 10–9 g, down to 10–12 g (where g = 9.8 m/s2 stands for the mean surface gravity). To this end, relative gravimeters must be accurately calibrated to retrieve reliable results from high-precision gravity monitoring. In an attempt to meet the requirements of the ongoing gravimetric studies in the Lake Nasser area, as the scale factors of the two gravimeters were not available, the first task we faced was to obtain a reliable calibration of the data acquired at the two permanent stations. We follow a theoretical approach for determination of the scaling (calibration) factor based on theoretical Earth tides as reference (Figs. 2d–f, 3d–f) which was first suggested by Goodkind (1996). Other than the theoretical Earth tides, gravity variations due to the atmosphere, hydrosphere, ocean and polar motion, have to be accounted for, because the raw gravity data also include these signals. In other words, we synthetize a reference signal, based on the Hartmann–Wenzel tidal catalogue HW95, which in principle should have an accuracy of 1 nGal (Hartman and Wenzel 1995a, b), and the Wahr–Dehant Earth tide model (WD model) (Dehant 1987) (Figs. 2d, 3d). To accomplish this task, we use ET34-ANA-V80 switched to “prediction mode” that allows the computation of body tides and OTL gravity effect of whatever station with a suitable sampling interval (Schüller, 2020). We have tested all three terrestrial models (DDW-H, DDW-NHi, WDZ-NHi) available in the software system, but a sensitivity test showed that the differences between the models are below the accuracy of the data collected, and hence are not significant. The adopted OTL (Figs. 2e, 3e) was a hybrid one coming from the average of two recent models accounting for both Mediterranean and Red seas, FES2014b (Carrere et al., 2015) and GOT99.2b (Ray, 1999). To include the atmospheric effect (Hinderer et al., 2014; Riccardi et al., 2007) in the synthetic reference signal, we just compute the gravity variations derived from the product of the nominal admittance coefficient -3.0 nm s−2 /hPa and the air pressure signal collected at both the stations (Figs. 2f, 3f). We discarded the use of site-dependent admittance factors determined at the stations because of the strong non-linearities observed in the response of the gravimeters to atmospheric pressure variations due to uncompensated Archimedean forces in not perfectly sealed spring gravimeters. This is a well-known behaviour, already observed by several authors (Meurers, 2018; Riccardi et al., 2002) in aged spring gravimeters. As a fact the LCR-ET gravimeters are not evacuated inside but should be set at the mean pressure for the station to minimize forces on the case which would deform those and lead to stresses in the structure. When the seals deteriorate with time and become leaky the ambient pressure causes air to move through the seals in both directions causing variable Archimedean forces on the mass, which are only partially mitigated by the buoyancy compensator mounted on the beam opposite from the mass. This effect can translate into phase shifts between inside and ambient outside pressure, making difficult to assess a local barometric admittance.

The determination of the scaling factor is performed by using two different approaches through: (1) a simple linear regression between the pre-processed (“cleaned”), raw high-pass filtered gravity data and the theoretical gravity variations at the site locations (Figs. 4, 6); (2) moving window linear regression (MWR) (Figs. 5, 7).

Fig. 4
figure 4

Aswan station: calibration of the LCR_ET16 feedback output voltage derived from regression against the synthetic reference signal; parameters of the linear fit are given too

Full size image
Fig. 5
figure 5

Aswan station: Moving window regression analysis of Synthetic reference signal vs. feedback output voltage with indication of the mean value (in red).

Full size image
Fig. 6
figure 6

Abu Simbel station: calibration of the LCR_D-218 feedback output voltage derived from regression against the synthetic reference signal; parameters of the linear fit are given too

Full size image

The last approach allows us to study the well-known apparent changes in sensitivity over time that severely limit the performance of spring gravimeters. This peculiar behaviour, mainly due to tilt variations and loss of verticality of recording spring gravimeters which are not equipped with active tilt compensation systems, has already been studied (Riccardi et al., 2002). Indeed, when a spring gravimeter with electrostatic feedback is tilted, it just measures the reduced gravity (g*cosα; α = tilt angle). Since a long gravity record is available, we decided to analyse the stability of the scaling factors over time. The data set was windowed and divided into subsets of 7 days, with 10% overlap, and linear regression analysis was applied on each set. The scaling factors resulting from the analysis display a clear temporal variability, sometimes greater than 5% (Figs. 5, 7).

Fig. 7
figure 7

Abu Simbel station: moving window regression analysis of Synthetic reference signal vs. feedback output voltage with indication of the mean value (in red)

Full size image

5 Results and Discussions

5.1 Calibration and Tidal Analyses

One of the main outcomes of the calibration experiments conducted on the two gravimeters is a large variability over time. The observed time variable instrumental sensitivity might be essentially due to the lack of compensation of tilt changes. If a gravimeter is tilted by an angle ϕ, from the local vertical, it measures the component of gravity gcosϕ, along its axis. For small angles, the apparent decrease in the gravity is about − 4.9 × 10−3 nms−2 rad−2. In order to avoid all these effects, superconducting gravimeters are provided with an active tilt feedback system designed to keep the meter aligned to the vertical to better than a few μradians. This device is servo-controlled to maintain level, allowing the gravity meter to measure continuously over long periods of time with suitable stability (Riccardi et al., 2009). Recently Microg-LaCoste (2017) has patented and produced Odin, a servo-controlled precision leveling and stabilizing platform for spring gravimeters and other instrumentation. Tilting is precisely controlled with sub-arcsecond resolution by means of three temperature controlled hydraulic legs.

The values derived from the averages of the moving window regressions were taken as scaling factors (Figs. 5, 7). The calibrated data were decimated to 3600 s, then tidal analyses were performed on the hourly gravity and atmospheric pressure variations acquired at the two stations using the software ET34-ANA-V80 (Schüller, 2020). Results for the main tidal waves are listed in Table 2, while deltas of the 5 largest waves are plotted in the Figs. 8a and 9a.

Fig. 8
figure 8

Aswan: observed and OTL corrected amplitude of the tidal gravimetric factor delta (a) and final residual OTL vector X (b) for the main tidal waves; convention of vector representation of Earth tide and ocean loading (c): R earth model tidal amplitude, A observed tidal amplitude, L OTL vector according to a specific model, X final residual vector

Full size image
Fig. 9
figure 9

Abu Simbel: observed and OTL corrected amplitude of the tidal gravimetric factor delta (a) and final residual OTL vector X (b) for the main tidal waves; convention of vector representation of Earth tide and ocean loading is depicted in Fig. 8c

Full size image

The comparison of the results (Table 2) clearly shows that the quality of the inferred tidal parameters is much higher for the Aswan station, where longer data sets (572 days) were available and acquired with a gravimeter specifically designed for tidal recordings (LCR_ET16). In Aswan the waves of greater amplitude (O1, K1, M2) have a percentage error of less than 1%, only K2 has a percentage error of 1.5%. In Abu Simbel, on the other hand, only the wave with the largest amplitude at these latitudes, i.e. M2, has an error of around 1%, while even waves with significant amplitudes have errors > 10%. The phase leads (φ) in Aswan are close to zero, while in Abu Simbel they are highly scattered, except for M2 and K1. A clear modulation due to the thermal influence at 24 h, coincident with the very small tidal component S1, can be envisaged in both stations, but in Abu Simbel such a modulation is dramatic (δS1 = 143). This station is in a desert area, just hosted in a small concrete shelter. A room thermometer installed onsite has recorded daily variations of several degrees and maximum temperatures up to 55 °C in summer. So direct and indirect (tilt changes) thermal effects are likely expected for this site, while in Aswan, the room temperature has an acceptable stability with recorded change less than 1 °C per day (Hassan et al., 2010a).

For a more quantitative assessment of the quality of the retrieved tidal parameters, the OTL correction has been applied (Figs. 8, 9). Considering the large distance of Aswan and Abu Simbel stations from the coast (400–500 km from the Red Sea, 900–1000 km from the Mediterranean Sea and nearly 1800 km from the Gulf of Aden, respectively) a very small ocean loading effect is predicted by the models (< 10 nm/s2 at M2 tidal period).

Since OTL effect is incorporated into the estimated tidal parameters, to separate body and ocean tides we have used ET34-ANA-V80 to compute the body tide, according to HW95 tidal potential catalogue and different Earth models, and OTL parameters provided by the online free ocean tide loading provider, hosted at Onsala Observatory (Bos & Scherneck, 2021). Amplitude and phase of the OTL effect on gravity are computed according to FES2014b (Carrere et al., 2015) and GOT99.2b (Ray, 1999) models, then the mean value of the two models is considered (Figs. 8, 9). The final residual vectors (\(\overrightarrow{{\varvec{X}}}\)) better elucidate the discrepancy between observed and modelled amplitude parameters (Figs 8b, 9b); the convention explaining the physical meaning of \(\overrightarrow{{\varvec{X}}}\) is depicted in Fig. 8c. For Aswan a good match can be deduced between the corrected and theoretical parameters for M2 and K2 and an acceptable agreement for O1 and K1 wave groups.

It is acknowledged that Melchior’s amplitude ratios δM2/δO1 and δO1/δK1 are useful for assessing to what degree the observed delta and those reduced by ocean load, will fit to a specified Earth model since these parameters should not depend on the calibration inaccuracies. Encouraging results turn out for Aswan. In fact, after the OTL correction, the best fitting model for δM2/δO1 turns out to be DDW-NHi model, with a relative deviation around − 2%, while the best fitting model for δO1/δK1 is DDW-H, having a very small relative deviation from model (− 0.030%). The results for Abu Simbel are still acceptable for δM2/δO1, the relative deviation from model DDW-NHi is − 2%, but for δO1/δK1 it is quite worse (16%), likely due to a bad determination of K1.

The different quality of the tidal models for Aswan and Abu Simbel is even confirmed by the spectral analysis of the gravity residuals (Fig. 10). Very low spectral energy remains in the diurnal and semidiurnal tidal bands (FFT amplitude < 0.5 μGal) after fitting the synthetic tide at Aswan (Fig. 10b). On the contrary, gravity residuals from Abu Simbel have spectral amplitude > 2 μGal in K1 tidal band as well as significant spectral amplitude in 3, 4, 5 cpd, namely sub-harmonics of 1 cpd, that might indicate a thermal modulation, as indicated even by the large δS1 outcoming from the tidal analyses.

Fig. 10
figure 10

Hourly gravity residuals for Aswan and Abu Simbel (a) and their Fourier amplitude spectra (log10 scale) (b); frequency units are cycles per day (cpd)

Full size image

However, as we were not satisfied with the results obtained at the Abu Simbel station with a land gravimeter LCR model D, new gravity records have been collected to validate and improve the poor tidal model obtained so far. To this end, it was decided to move the LCR_ET16 gravimeter from Aswan to Abu Simbel. At the time of submission of this manuscript, time series from 20 October 2021 to 31 January 2022 (approximately 90 days) were acquired.

As done previously, the collected recordings were converted into gravity signals by deriving a scaling factor from a regression analysis against a synthetic reference signal, whose construction has been described above. Again, as before, two approaches have been followed for this: (a) a simple regression of the high-pass filtered signal against the synthetic one; (b) a MWR analysis. This last method enabled us to show a strong variability of the scaling factors (Fig. 11b) especially after a re-centering operation of the feedback voltage by the operator that is needed due to the strong instrument drift. To estimate which of the two approaches is the most effective, residuals were calculated by tidal adjustment using ET34-X-V80 (Fig. 11a, c). The results clearly show that MWR gives better results by allowing residuals with lower energy in both diurnal and semi-diurnal spectral bands (Fig. 11d). Anyway, the analysis of this series, although short, allowed us to confirm the superiority of the ET gravimeter (LCR_ET16) compared to a land gravimeter and to resolve at least the main tidal components in the diurnal and semidiurnal bands. According to Rayleigh's criterion, it was not possible to separate the band (P1S1K1; S2K2) and other important but smaller amplitude waves. However, the quality of the results for the resolved waves clearly shows the higher precision of the tidal model obtainable with the LCR_ET16, compared to the one retrieved from the LCR_D-218 records. Results from the new station at Abu Simbel are listed in Table 3 and deltas of the 4 largest waves are plotted in the Fig. 12a; a simple comparison with these results with those reported in Table 2 and Fig. 9 confirms what was described before. The significant temporal evolution of the scaling factor (Fig. 11b), in particular, the clear decrease linked to the re-centering of the feedback, following the intervention of the operator, is very likely due to a disturbance of the tilt with loss of verticality of the instrument that is not installed on a self-levelling plate. Actually, we cannot rule out that the increase of the residual amplitudes with time (Fig. 11a), coincident with the increase of the apparent scale factor (Fig. 11b), could even be an indication of nonlinear behaviour of the electrostatic feedback. We attempted to account for the non-linearity of the electrostatic feedback by means of a calibration function determined by Walter Zürn in 2015. However, the results obtained lead to delta factor values that are much larger than the theoretical ones, leading to residual X-vectors that are an order of magnitude larger than those obtained by linearly calibrating against the synthetic tidal signal.

Fig. 11
figure 11

Gravity residuals after fitting a tidal model assessed with ET34-v80 software on the new station realized in Abu Simbel with the LCR_ET16 gravimeter by considering two calibration approaches: single scale factor (a), MWR results and calibration function (b), calibration function retrieved from the MWR analysis (c), Fourier amplitude spectra of the residuals (d)

Full size image
Table 3 Tidal parameters (δ and φ) and their statistical quality (RMS, error) for the main tidal waves retrieved from the tidal analyses carried out on the gravity records collected on the new gravity station at Abu Simbel between 20 October 2021 and 31 January 2022
Full size table
Fig. 12
figure 12

The new Abu Simbel station, first record (90 days): observed and OTL corrected tidal factors delta (a) and final residual OTL vector X (b) for the largest resolved tidal waves; refer to Fig. 8c for the convention of the vector representation of the body tide and ocean load

Full size image

5.2 Gravity Residuals and Lake Nasser Level Changes

The residual signal retrieved after tidal subtraction is in the range of ± 50 µGal for both the stations (Fig. 10a). As we have mainly focused on the assessment of a reliable tidal model for the region, little attention has been paid to the analysis of long-term gravity variation. We merely filtered out the long-term variations without attempting a separation between instrumental drift and actual gravity variations. We are aware that by filtering out the long-term part, there is a risk of also suppressing useful signals from the lake.

So, we have tried reconstructing the long-term gravity change by summing up the gravity residuals and drift, the latter being converted in gravity units by means of the scale factors. Then a tentative comparison of gravity residuals with Lake Nasser level changes is carried out. For this comparison we have used the altimetric data (Fig. 13a), freely available online at G-REALM (2021). Data come from the merging of 3 satellite missions TOPEX/Poseidon/Jason satellite series (at 10-day resolution), the ERS/ENVISAT/SARAL series (at 35-day resolution) and the Sentinel-3 series (at 27-day resolution). Data fusion leads to a final time resolution of 10 days of the altimetry time series. To place this comparison in the right context, the reader should bear in mind that the level variations come from satellite altimetry observations referring to a benchmark with coordinates 23.290° N, 32.850° E (red spot in Fig. 1), while the best station we are using for the comparison is Aswan (see Table 1 for its coordinates), about 70 km to the north. The satellite altimetry data (Fig. 13a) very clearly show the four stages of seasonal modulations of the water level (inflow, stability, discharge, and back to stability) related to the Aswan High Dam operations.

Fig. 13
figure 13

Lake Nasser height variations since 1992 computed from satellite altimetry data sets freely available at G-REALM web page (a), height variation in the time windows encompassing this study (b), tentative long term gravity changes (gravity residuals + drift) at Aswan (c), gravity residuals after subtracting tides from the gravity records (d); height changes are referred to EGM08 datum

Full size image

Comparing changes in lake level with gravity residuals shows that they look completely uncorrelated (Fig. 13d), while a certain correlation can be glimpsed with the signals obtained by summing up residuals and drift (Fig. 13c), but we can just speculate about a temporal correlation, because we cannot be sure about the amplitude of the measured gravity changes. This hindering element is essentially due to the highly nonlinear behaviour of the instrument drift of the ET spring gravimeters. Actually, the high order polynomial drift could quietly mask the targeted hydrological seasonal signals. From the literature we know that the expected gravity signals due to the water level change in the lake should be in the order of tens of μGal (Hassan et al., 2010b), while the resulting gravity signal (residuals + drift) at Aswan is in the order of hundreds of μGal.

6 Conclusions

Gravity recordings conducted over a period of about 3 years have allowed us to recover an acceptable tidal model for Aswan. We believe that part of the resulting discrepancies between the observed and theoretical tidal parameters could also result from the load exerted by the variation of the lake Nasser level but taking into account the performance of the spring gravimeters, no firm conclusion can be drawn on this point. Clearly, two main factors could be responsible for the discrepancies between the observed and theoretical tidal parameters: a Newtonian effect due to the mass of the lake and its indirect variable loading during the loading and unloading of the lake significantly changes the gravity field in and around the lake. Modelling of these phenomena, done in previous studies (Hassan et al., 2010b), has shown that changes in lake level can produce up to 30 µGal. This could also explain the discrepancies in the tidal parameters obtained at Aswan and Abu Simbel. Nor can we exclude that some of these discrepancies may also be due to poor modelling of atmospheric loading. The latter effect was not adequately investigated during this study due to the poor performance of the old spring gravimeters used.

With the relocation of LCR_ET16 to Abu Simbel at the end of October 2021, a new record has been set up and has started to provide promising results. After almost 2.5 months of gravity recording, we have retrieved adequate tidal factors at least for the main waves (Q1, O1, K1, M2, S2), with an accuracy even better than that obtained in Aswan with the same instrument. In fact, this result was expected given the remote location of the site, in a desert area, far from any anthropogenic activities.

Concerning the retrieved gravity residuals, we believe that further analyses of the instrumental contribution are needed before to be able to interpret this gravity signal as due to surface or underground hydrology.

We guess that most of the observed long-term gravity changes should have an instrumental origin. This is the reason why our main suggestion is to replace the spring sensors operating in Abu Simbel or Aswan with a higher quality superconducting gravimeter. The state of art (e. g. Chaffaut et al., 2022; Creutzfeld et al., 2010) testifies that thanks to an extremely low and stable instrumental drift, the superconducting gravimeters are very suitable for catching hydrological signals. For example, important achievements have been reported in Djougou (Benin, West Africa) for the study of the monsoon hydrological cycle. The water storage changes were assessed by adopting a hybrid gravimetric approach, namely by using both absolute and relative gravity sensors, where 8 years of continuous superconducting gravity record had a pivotal role (Hinderer et al., 2020).

Installing a superconducting gravimeter for instance in Abu Simbel, which is located in a desert area, with very low noise level, could have several applications. First of all, to study with suitable signal-to-noise ratio and adequate temporal resolution the hydrological cycle due to Lake Nasser; retrieving more precise tidal parameters; studying tectonic activity in an area of relevant seismogenic interest, such as the Kalabsha fault. It could also be interesting to investigate some peculiar characteristics of atmospheric pressure changes in the tropical/equatorial belt and, last but not least, it could also be the first superconducting gravity station in the North African- Middle East region.