Skip to main content
SpringerLink
Log in

Simulation of Strong Ground Motion of the 2009 Bhutan Earthquake Using Modified Semi-Empirical Technique

  • Published:
Pure and Applied Geophysics Aims and scope Submit manuscript

Abstract

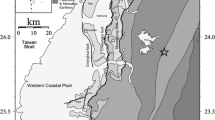
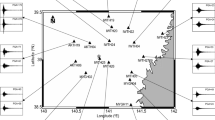
On 21st September 2009 an earthquake of magnitude (M w 6.1) occurred in the East Bhutan. This earthquake caused serious damage to the residential area and was widely felt in the Bhutan Himalaya and its adjoining area. We estimated the source model of this earthquake using modified semi empirical technique. In the rupture plane, several locations of nucleation point have been considered and finalised based on the minimum root mean square error of waveform comparison. In the present work observed and simulated waveforms has been compared at all the eight stations. Comparison of horizontal components of actual and simulated records at these stations confirms the estimated parameters of final rupture model and efficacy of the modified semi-empirical technique (Joshi et al., Nat Hazards 64:1029–1054, 2012b) of strong ground motion simulation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  • Ambraseys, N., & Jackson, D. (2003). A note on early earthquakes in northern India and southern Tibet. Current Science, 84, 570–582.

    Google Scholar 

  • Angelier, J., & Baruah, S. (2009). Seismotectonics of northeast India: a stress analysis of focal mechanism solutions of earthquakes and its kinematic implications. Geophysical Journal International. doi:10.1111/j.1365-246X.2009.04107.x.

    Google Scholar 

  • Boore, D. M. (1983). Stochastic simulation of high frequency ground motion based on seismological models of radiated Spectra. Bull Seism Soc Am, 73, 1865–1894.

    Google Scholar 

  • Brune, J. N. (1970). Tectonic stress and spectra of seismic shear waves from earthquakes. Journal of Geophysical Research, 75, 4997–5009.

    Article  Google Scholar 

  • Diehl, T., Singer, J., Kissling, E., Hetényi, G., & Clinton, J., (2015). Inferring seismicity and crustal structure by applying state-of-the-art seismic network analysis to a temporary array in Bhutan, IUGG Conference, Prague 2015.

  • Fukuyama, E., & Irikura, K. (1986). Rupture process of the 1983 Japan sea (Akita-Oki) earthquake using a waveform inversion method. Bulletin of the Seismological Society of America, 76, 1623–1640.

    Google Scholar 

  • Gahalaut, V. K., Rajput, S., & Kundu, B. (2011). Low seismicity in Bhutan Himalaya and stress shadow of 1897 Shillong plateau earthquake. Physics of the Earth and Planetary Interiors, 186(3–4), 97–102.

    Article  Google Scholar 

  • Irikura, K., Kagawa, T., & Sekiguchi, H., (1997). Revision of the empirical Green’s function method by Irikura, 1986. Programme and Abstracts. The Seismological Society of Japan, 2, B25.

  • Irikura, K., & Kamae, K. (1994). Estimation of strong ground motion in broad-frequency band based on a seismic source scaling model and an Empirical Green’s function technique. Annals of Geophysics, 37(6), 1721–1743.

    Google Scholar 

  • Joshi, A. (2001). Strong motion modeling of the source of the Chamoli earthquake of March 29, 1999 in the Garhwal Himalaya, India. Journal of Seismology, 5, 499–518.

    Article  Google Scholar 

  • Joshi, A. (2004). A simplified technique for simulating wide band strong ground motion for two recent Himalaya earthquakes. Pure and Applied Geophysics, 161, 1777–1805.

    Article  Google Scholar 

  • Joshi, A., Kumar, B., Sinvhal, A., & Sinvhal, H. (1999). Generation of synthetic accelerograms by modelling of rupture plane. Journal of Earthquake Technology, 36, 43–60.

    Google Scholar 

  • Joshi, A., Kumari, P., Sharma, M. L., Ghosh, A. K., Agarwal, M. K., & Ravikiran, A. (2012a). A strong motion model of the 2004 great Sumatra earthquake: simulation using a modified semi empirical method. Journal of Earthquake and Tsunami, 6, 1–29.

    Article  Google Scholar 

  • Joshi, A., Kumari, P., Singh, S., & Sharma, M. L. (2012b). Near-field and far-field simulation of accelerograms of Sikkim earthquake of September 18, 2011 using modified semi-empirical approach. Natural Hazards, 64, 1029–1054.

    Article  Google Scholar 

  • Joshi, A., Kuo, C. H., Dhibar, P., Sandeep, Sharma, M. L., Wen, K. L., et al. (2015). Simulation of the records of the 27th March 2013, Nantou Taiwan earthquake using modified semi-empirical approach. Natural Hazard, 78, 995–1020.

    Article  Google Scholar 

  • Joshi, A., & Midorikawa, S. (2004). A simplified method for simulation of strong ground motion using rupture model of the earthquake source. Journal of Seismology, 8, 467–484.

    Article  Google Scholar 

  • Joshi, A., & Mohan, K. (2010). Expected peak ground acceleration in Uttarakhand Himalaya, India region from a deterministic hazard model. Natural Hazards, 52, 299–317.

    Article  Google Scholar 

  • Joshi, A., & Patel, R. C. (1997). Modelling of active lineaments for predicting a possible earthquake scenario around Dehradun, Garhwal Himalaya, India. Tectonophysics, 283, 289–310.

    Article  Google Scholar 

  • Joshi, A., Sandeep, & Kamal, (2014). Modeling of strong motion generation areas of the 2011 Tohoku, Japan earthquake using modified semi empirical technique. Natural Hazards, 71, 587–609.

    Article  Google Scholar 

  • Joshi, A., Singh, S., & Giroti, K. (2001). The Simulation of ground motions using envelope summations. Pure and Applied Geophysics, 158, 877–901.

    Article  Google Scholar 

  • Joyner, W.B., & Boore, D.M., (1988). Measurement, characterization and prediction of strong ground motion. In Proc. of earthquake engineering and soil dynamics II (pp. 43–102), ASCE Utah, June 27–30.

  • Kameda, H., & Sugito, M. (1978). Prediction of strong earthquake motions by evolutionary process model. In: Proceedings of the sixth Japan earthquake engineering symposium (pp. 41–48).

  • Kanamori, H., & Anderson, D. L. (1975). Theoretical basis of some empirical relations in seismology. Bulletin of the Seismological Society of America, 65, 1073–1095.

    Google Scholar 

  • Kayal, J. R. (1996). Earthquake source process in northeast India: a review. Journal of Himalayan Geology, 17, 53–69.

    Google Scholar 

  • Kayal, J. R. (2001). Microearthquake activity in some parts of the Himalaya and the tectonic model. Tectonophysics, 339, 331–351.

    Article  Google Scholar 

  • Kayal, J. R. (2008). Microearthquake seismology and seismotectonics of South Asia. Heidelberg, Germany: Springer.

    Google Scholar 

  • Kayal, J. R. (2010). Himalayan tectonic model and the great earthquakes: an appraisal. Geomatics, Natural Hazards and Risk, 1, 50–62.

    Google Scholar 

  • Kayal, J. R., Sergei, S. A., Baruah, S., Tatevossian, R., Gogoi, N., Sanoujam, M., et al. (2010). The 2009 Bhutan and Assam felt earthquakes (M w 6.3 and 5.1) at the Kopili fault in the northeast Himalaya region. Geomatics, Natural Hazards and Risk, 1(3), 273–281.

    Article  Google Scholar 

  • Kumar, D., Teotia, S. S., & Khattari, K. N. (1997). The representation of attenuation characteristics of strong ground motion observed in the 1996 Dharamshala and 1991 Uttarkasshi earthquakes by available empirical relations. Current Science, 73, 543–548.

    Google Scholar 

  • Mittal, H., Kumar, A., & Ramhmachhuani, R. (2012). Indian national strong motion instrumentation network and site characterization of its stations. International Journal of Geosciences, 3, 1151–1167.

    Article  Google Scholar 

  • Mukhopadhyay, B., Acharyya, A., & Dasgupta, S. (2011). Potential source zones for Himalayan earthquakes: constraints from spatial–temporal clusters. Natural Hazards, 57, 369–383.

    Article  Google Scholar 

  • Oldham, R. D. (1899). Report on the great earthquake of the 12th June 1897. Memoirs of the Geological Survey of India Publishing Memoirs 29, reprinted 1981. Calcutta: Geological Survey of India.

    Google Scholar 

  • Sandeep, Joshi, A., Kamal, Kumar, P., Kumar, A., & Dhibar, P. (2015). Modeling of strong motion generation areas of the Niigata, Japan, earthquake of 2007 using modified semi empirical technique. Natural Hazards, 77, 933–957.

    Article  Google Scholar 

  • Sandeep, A. Joshi, Kamal, P., & Kumar, A. Kumar. (2014a). Effect of frequency dependent radiation pattern in simulation of high frequency ground motion of Tohoku earthquake using modified semi empirical method. Natural Hazards, 73, 1499–1521.

    Article  Google Scholar 

  • Sandeep, A. Joshi, Kamal, P., & Kumar, P. Kumari. (2014b). Modeling of strong motion generation area of the Uttarkashi earthquake using modified semi-empirical approach. Natural Hazards, 73, 2041–2066.

    Article  Google Scholar 

  • Somerville, P. (1993). Engineering applications of strong ground motion simulation. Tectonophysics, 218(1–3), 195–219.

    Article  Google Scholar 

  • Tandon, A. N. (1954). A study of Assam earthquake of August 1950 and its aftershocks. Indian Journal of Meteorology, Hydrology and Geophysics, 5, 95–137.

    Google Scholar 

  • Wells, L. D., & Coppersmith, K. J. (1994). New empirical relationships among magnitude, rupture length, rupture width, rupture area and surface displacement. Bulletin of the Seismological Society of America, 84, 974–1002.

    Google Scholar 

  • Yu, G. (1994), Some aspects of earthquake seismology: slip portioning along major convergent plate boundaries: composite source model for estimation of strong motion and nonlinear soil response modeling. Ph.D. thesis, University of Nevada.

  • Yu, G., Khattri, K. N., Anderson, J. G., Brune, J. N., & Zeng, Y. (1995). Strong ground motion from the Uttarkashi earthquake, Himalaya, India, earthquake: comparison of observations with synthetics using the composite source model. Bulletin of the Seismological Society of America, 85, 31–50.

    Google Scholar 

  • Zeng, Y., Anderson, J. G., & Yu, G. (1994). A composite source model for computing realistic synthetic strong ground motions. Geophysical Research Letters, 21(8), 725–728.

    Article  Google Scholar 

Download references

Acknowledgments

The authors are highly thankful to the anonymous reviewers and Editor Dr. Fabio Romanelli for their valuable suggestions. Accelerograms data used in this study obtained from http://www.pesmos.in are thankfully acknowledged. The work presented in this paper is an outcome of the sponsored project from Science and Engineering Research Board, DST, with project reference no. ECR/2016/000737 and from Ministry of Earth Sciences project reference no. MoES/P.O.(Seismo)/1(42)/2009. The authors sincerely thank Dept. of Geophysics, Institute of Science, Banaras Hindu University, Varanasi and Dept. of Earth Sciences IIT Roorkkee for providing basic facilities for this research work. The author Dr. Parveen Kumar sincerely acknowledged Director, Wadia Institute of Himalayan Geology, Dehradun.

Author information

Authors and Affiliations

  1. Department of Geophysics, Banaras Hindu University, Varanasi, India

    Sandeep & S. K. Sah

  2. Department of Earth Sciences, Indian Institute of Technology Roorkee, Roorkee, India

    A. Joshi, Sohan Lal &  Kamal

  3. Wadia Institute of Himalayan Geology, Dehradun, India

    Parveen Kumar

  4. Ministry of Earth Sciences, New Delhi, India

    Vandana

Authors
  1. Sandeep
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. Joshi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Sohan Lal
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Parveen Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. S. K. Sah
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Vandana
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Kamal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sandeep.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sandeep, Joshi, A., Lal, S. et al. Simulation of Strong Ground Motion of the 2009 Bhutan Earthquake Using Modified Semi-Empirical Technique. Pure Appl. Geophys. 174, 4343–4356 (2017). https://doi.org/10.1007/s00024-017-1663-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00024-017-1663-2

Keywords

Search

Navigation