Skip to main content
SpringerLink
Log in

Impact of Three-Parameter Weibull Models in Probabilistic Assessment of Earthquake Hazards

  • Published:
Pure and Applied Geophysics Aims and scope Submit manuscript

Abstract

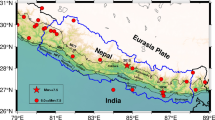
This paper investigates the suitability of a three-parameter (scale, shape, and location) Weibull distribution in probabilistic assessment of earthquake hazards. The performance is also compared with two other popular models from same Weibull family, namely the two-parameter Weibull model and the inverse Weibull model. A complete and homogeneous earthquake catalog (Yadav et al. in Pure Appl Geophys 167:1331–1342, 2010) of 20 events (M ≥ 7.0), spanning the period 1846 to 1995 from north–east India and its surrounding region (20°–32°N and 87°–100°E), is used to perform this study. The model parameters are initially estimated from graphical plots and later confirmed from statistical estimations such as maximum likelihood estimation (MLE) and method of moments (MoM). The asymptotic variance–covariance matrix for the MLE estimated parameters is further calculated on the basis of the Fisher information matrix (FIM). The model suitability is appraised using different statistical goodness-of-fit tests. For the study area, the estimated conditional probability for an earthquake within a decade comes out to be very high (≥0.90) for an elapsed time of 18 years (i.e., 2013). The study also reveals that the use of location parameter provides more flexibility to the three-parameter Weibull model in comparison to the two-parameter Weibull model. Therefore, it is suggested that three-parameter Weibull model has high importance in empirical modeling of earthquake recurrence and seismic hazard assessment.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Abernethy, R. B. (2006), The new Weibull handbook, 5th Ed., North Palm Beach, FL 33408-4328, pp. 536.

  • Akaike, H. (1974), A new look at the statistical model identification, IEEE Trans. Auto. Control 19(6), 716–723.

    Google Scholar 

  • Aldrich, J. (1997), R. A. Fisher and the making of maximum likelihood 1912–1922, Statist. Sci. 12(3), 162–176.

    Google Scholar 

  • Almeida, J. B. (1999), Application of Weibull statistics to the failure of coatings, J. Material Process. Tech. 93, 257–263.

  • Anagnos, T. and Kiremidjian, A. S. (1984), A stochastic time predictable model for earthquake occurrences, Bull. Seismol. Soc. Am. 74, 2593–2611.

    Google Scholar 

  • Anagnos, T. and Kiremidjian, A. S. (1988), A review on earthquake occurrence models for seismic hazard analysis, Prob. Engg. Mech. 3(1), 3–11.

  • Anderson, G. (1994), Simple tests of distributional form, J. Econometrics 62, 265–276.

    Google Scholar 

  • Baker, J. W. (2008), An introduction to probabilistic seismic hazard analysis, version 1.3; http://www.stanford.edu/~bakerjw/Publications/Baker_(2008)_Intro_to_PSHA_v1_3.pdf (retrieved on July 25, 2012).

  • Bartolucci, A. A., Singh, K. P., Bartolucci, A. D., and Bae, S. (1999), Applying medical survival data to estimate the three-parameter Weibull distribution by the method of probability-weighted moments, Maths. Comp. Simulation 48, 385–392.

  • Bhatia, S. C., Kumar, R. M., and Gupta H. K. (1999), A Probabilistic Seismic Hazard Map of India and Adjoining Regions, Annals Geophys. 42(6), 1153–1164.

  • Bis. (2002), IS 1893 (part 1)-2002: Indian standard criteria for earthquake resistant design of structures, part 1 – general provisions and buildings, Bureau of Indian Standards, New Delhi.

  • Blischke, W. R. (1974), On non-regular estimation. II. estimation of the location parameter of the gamma and Weibull distributions, Comm. Statist. 3, 1109–1129.

    Google Scholar 

  • Boero, G., Smith, J. and Wallis, K. F. (2004), The sensitivity of Chi squared goodness-of-fit tests to the partitioning of data, Econometric Reviews 23, 341–370.

  • Burnham, K. P. and Anderson, D, R. (2002), Model selection and multimodel inference: practical information—theoretic approach, 2nd ed., Springer-Verlag.

  • Burnham, K. P. and Anderson, D, R. (2004), Multimodel inference: understanding AIC and BIC in model selection, Sociological Methods and Research 33, 261–304.

  • Cheng, R. C. H., Evans, B. E., and Iles, T. C. (1992), Embedded models in nonlinear regression, J. Royal Statist. Soc. 54, 877–888.

  • Cornell, C. A. (1968), Engineering seismic risk analysis, Bull. Seismol. Soc. Am. 58, 1583–1606.

  • Cousineau, D. (2009), Fitting the three-parameter Weibull distribution: review and evaluation of existing and new methods, IEEE Trans. on Dielectrics and Electrical Insulation 16 (1), 281–288.

    Google Scholar 

  • Cousineau, D., Brown, S., and Heathcote, A. (2004), Fitting distributions using maximum likelihood: methods and packages, Behavior Research Methods, Instruments & Computers 36, 742–756.

  • Cox, D. R. (1962), Further results on tests of separate families of hypothesis, J. Royal Statist. Soc., Ser. B 24, 406–424.

    Google Scholar 

  • Cramer, C. H., Petersen, M.D., and Reichle, M.S. (1996), A Monte Carlo approach in estimating uncertainty for a seismic hazard assessment of Los Angeles, Ventura, and Orange Counties, California, Bull. Seismol. Soc. Am. 86, (Dec. issue).

  • Cramer, H. (1946), Mathematical methods of statistics, Princeton, NJ: Princeton Univ. Press.

  • Dahiya, R. C. and Gurland, J. (1973), How many classes in the Pearson Chi square test? J. Am. Statist. Assoc. 71, 340–344.

  • Das, S., Gupta, I. D., and Gupta, V. K. (2006), A probabilistic seismic hazard analysis of northeast India, Earthq. Spectra, 22(1), 1–27.

    Google Scholar 

  • Das, S., Gupta, V. K., and Gupta, I. D. (2005), Codal provisions of seismic hazard in northeast India, Curr. Sci. 89(12), 2004–2008.

    Google Scholar 

  • Dey, A. K. and Kundu, D. (2010), Discriminating between the log-normal and log-logistic distribution, Comm. Statist. – Theory Methods. 39, 280–292.

    Google Scholar 

  • Drapella, A. (1993), Complementary Weibull distribution: unknown or just forgotten, Qual. Reliab. Engg. Int. 9, 383–385.

  • Dubey, S. D. (1967), Some percentile estimators for Weibull parameters, Technometrics 9, 119–129.

  • Efron, B. and Johnstone, I. (1990), Fisher information in terms of the hazard function, Annals Statist. 18, 38–62.

    Google Scholar 

  • Faenza, L., Hainzl, S., and Scherbaum, F (2009), Statistical analysis of the central Europe seismicity, Tectonophysics 470, 195–204.

  • Faenza, L., Marzocchi, W., Serretti, P., and Boschi, E. (2008), On the spatio- temporal distribution of M 7.0+ worldwide seismicity, Tectonophysics 449, 97–104.

  • Ferraes, S.G. (2003), The conditional probability of earthquake occurrence and the next large earthquake in Tokyo, Jpn J. Seismol. 7, 145–153.

    Google Scholar 

  • Fisher, R. A. (1912), On an absolute criterion for fitting frequency curves, Messenger of Mathematics 41, 155–160.

  • Fisher, R. A. (1922a), On the mathematical foundations of the theoretical statistics, Philos. Trans. Roy. Soc. London Ser. A 222, 309–368.

  • Fisher, R. A. (1922b), The goodness of fit of regression formulae, and the distribution of regression coefficients, J. Royal Statist. Soc. 85, 597–612.

    Google Scholar 

  • Gumbel, E. J. (1943), On the reliability of the classical Chi square test, Annals of Math. Statist. 14, 253–263.

  • Gupta, H. K., Rajendran, K., and Singh, H. N. (1986), Seismicity of the northeast India region: Part I: the data base, J. Geol. Soc. India 28, 345–365.

    Google Scholar 

  • Gupta, R. D. and Kundu, D. (1999), Generalized exponential distribution, Aust. NZ. J. Statist. 41, 173–188.

  • Gupta, R. D. and Kundu, D. (2006), On the comparison of Fisher information of the Weibull and GE distributions, J. Statist. Plann. Inf. 136, 3130–3144.

    Google Scholar 

  • Hamdan, M. A. (1963), The number and width of classes in Chi square test, J. Am. Statist. Assoc. 58, 678–689.

    Google Scholar 

  • Heo, J. H., Boes, D. C., and Salas, J. D. (2001), Regional flood frequency analysis based on a Weibull Model: Part 1, Estimation and Asymptotic Variances, J. Hydro. 242, 157–170.

    Google Scholar 

  • Hirose, H. (1996), Maximum likelihood estimation in the 3-parameter Weibull Distribution: a look through the generalized extreme value distribution, IEEE Trans. Dielectr. Electr. Insul. 3, 43–55.

    Google Scholar 

  • Hirose, H. (1999), Bias correction for the maximum likelihood estimates in the two-parameter Weibull distributions, IEEE Trans. Dielectr. Electr. Insul. 6, 66–68.

    Google Scholar 

  • Hogg, R. V., Mckean, J. W., and Craig, A. T. (2005), Introduction to mathematical statistics, 6th Ed., PRC Press, pp. 718.

  • Huillet, T. and Raynaud, H. F. (1999), Rare events in a Log-Weibull Scenario – application to earthquake magnitude data, European Physical Journal B 12, 457–469.

  • Hurvich, C. M. and Tsai, C. L. (1989), Regression and time series model selection in small samples, Biometrika 76, 297–307.

  • Hurvich, C. M. and Tsai, C. L. (1995), Model selection for extended quasi-likelihood models in small samples, Biometrics 51, 1077–1084.

  • Jiang, H., Sano, M., and Sekine, M. (1997), Weibull raindrop-size distribution and its application to rain attenuation, IEEE Proceedings – Microwaves, Antennas and Propagation 144, 197–200.

    Google Scholar 

  • Jiang, R. (1996), Failure models involving two Weibull distributions, PhD Thesis, University of Queensland, Australia.

  • Jiang, R., Murthy, D. N. P., and Ji, P. (2001), Models involving two inverse Weibull distributions, Reliab. Eng. Syst. Saf. 73, 73–81.

    Google Scholar 

  • Jiang, R., Zuo, M. J., and Li, H. X. (1999), Weibull and Weibull inverse mixture models allowing negative weights, Reliab. Eng. Syst. Saf. 66, 227–234.

  • Johnson, N. L., Kotz, S., and Balakrishnan, N. (1995), Continuous univariate distributions, Vol. 2, 2nd Ed., New York: Wiley.

  • Kagan, Y.Y. and Jackson, D.D. (1991), Long-term earthquake clustering, Geophys. J. Int. 104, 117–133.

    Google Scholar 

  • Kagan, Y.Y. and Jackson, D.D. (2000), Probabilistic forecasting of earthquakes, Geophys. J. Int. 143, 438–453.

    Google Scholar 

  • Kagan, Y.Y. and Jackson, D.D. (2011), Global earthquake forecasts, Geophys. J. Int. 184(2), 759–776.

  • Keller, A. Z. and Kamath, A. R. (1982), Reliability analysis of CNC machine tools, Reliab. Eng. 3, 449–473.

  • Khan, M. S., Pasha, G. R., and Pasha, A. H. (2008), Theoretical analysis of inverse Weibull distribution, Wseas Trans. on Maths. 7(2), 30–38.

  • Kijko, A. (2000), Statistical estimation of maximum regional earthquake magnitude m max , Workshop on Seismicity Modeling in Seismic Hazard Mapping, Poljce, Slovenia, 22–24.

  • Kijko, A. and Sellevoll, M. A. (1981), Triple exponential distribution, a modified model for the occurrence of large earthquakes, Bull. Seismol. Soc. Am. 71, 2097–2101.

    Google Scholar 

  • Kijko, A. and Sellevoll, M. A. (1992), Estimation of earthquake hazard parameters from incomplete data files. Part ΙΙ, incorporation of magnitude heterogeneity, Bull. Seismol. Soc. Am. 82(1), 120–134.

    Google Scholar 

  • King, J. R. (1971), Probability charts for decision making, Industrial Press, New York.

  • Kiremidjian, A.,and Anagnos, T. (1984), Stochastic slip-predictable model for earthquake occurrences, Bull. Seismol. Soc. Am. 74, 739–755.

    Google Scholar 

  • Knopoff, L. A. (1971), A Stochastic model for the occurrence of main sequence earthquakes, Rev. Geol. Space Phys. 9, 175–188.

    Google Scholar 

  • Koelher, K. J. and Gan, F. F. (1990), Chi squared goodness of fit test: cell selection and power, Comm., Statist. B. 19, 1265.

  • Kolmogorov, A. (1933), Sulla determinazione empirica di una legge di distribuzione (Italian), J. Inst. Ital. Atturi. 4:83.

    Google Scholar 

  • Kundu, D. and Manglick, A. (2004), Discriminating between the Weibull and log-normal distributions, Naval Res. Logistics 51, 893–905.

    Google Scholar 

  • Kundu, D. and Raqab, M. Z. (2009), Estimation of three parameter Weibull distribution, Statist. Prob. Let. 79, 1839–1846.

  • Kundu, D., Gupta, R. D., and Manglick, A. (2005), Discriminating between the log-normal and the generalized Exponential distributions, J. Statist. Planning and Inference 127, 213–227.

    Google Scholar 

  • Lawless, J. F. (1982), Statistical models and methods for lifetime data, Wiley, New York.

  • Lehmann, E. L. (1998), Theory of point estimation, Wiley, New York, pp. 616.

  • Mann, H. B. and Wald, A. (1942), On the choice of the number of class intervals in the application of the Chi square test, Annals Math. Statist. 13, 306–317.

  • Marshal, A. W., Meza, J. C., and Olkin, I. (2001), Can data recognize its parent distribution? J. Comp. Graphical Statist. 10, 555–580.

    Google Scholar 

  • Marzocchi, W. and Lombardi, A. M. (2008), A double branching model for earthquake occurrence, J. Geophy. Res. 113, 1–12.

    Google Scholar 

  • Massey, F. J. (1951), The Kolmogorov-Smirnov test for goodness of fit, J. Am. Statist. Assoc., 46(253), 68–78.

    Google Scholar 

  • Matthews, M. V., Ellsworth, W. L., and Reasenberg, P. A. (2002), A Brownian model for recurrent earthquakes, Bull. Seismol. Soc. Am. 92(6), 2233–2250.

  • Molnar, P. (1979), Earthquake recurrence intervals and plate tectonics, Bull. Seismol. Soc. Am. 69(1), 115–133.

    Google Scholar 

  • Mudholkar, G. S. and Kollia, G. D. (1994), Generalized Weibull family: a structural analysis, Comm. Statist. Series A: Theory and Methods 23, 1149–1171.

  • Mudholkar, G. S. and srivastava, D. K. (1993), Exponentiated Weibull family for analyzing bathtub failure-rate data, IEEE Trans. on Reliability 42(2), 299–302.

    Google Scholar 

  • Mudholkar, G. S., Srivastava, D. K., and Fremier, M. (1995), The exponentiated Weibull Family: a reanalysis of the bus motor failure data, Technometrics 37(4), 436–445.

    Google Scholar 

  • Mulargia, F. and Tinti, S. (1985), Seismic sample area defined from incomplete catalogs: an application to the Italian territory, Phys. Earth Planetroy Sci. 40(4), 273–300.

    Google Scholar 

  • Murthy, D. N. P., Xie M., and Jiang R. (2004), Weibull models, John Wiley and Sons, New Jersey, 1st Ed., pp.383.

  • Nelson, W. (1982), Applied life data analysis, Wiley, New York.

  • O’connor, D. T. P. (1997), Practical reliability engineering, Wiley, New York.

  • Ogata, Y. (1988), Statistical models for earthquake occurrences and residual analysis for point processes, J. Am. Stat. Assoc. 83(401), 9 – 27.

    Google Scholar 

  • Ogata, Y. (1999), Seismicity analysis point-process modeling: a review, Pure Appl. Geophys. 155, 471–507.

    Google Scholar 

  • Parvez, I. A. and Ram, A. (1997), Probabilistic Assessment of earthquake hazards in the north-east Indian Peninsula and Hindukush regions, Pure Appl. Geophys. 149, 731–746.

    Google Scholar 

  • Parvez, I. A. and Ram, A. (1999), probabilistic assessment of earthquake hazards in the Indian subcontinent, Pure Appl. Geophys. 154, 23–40.

  • Rao, C. R. (1945), Information and the accuracy attainable in the estimation of statistical parameters, Bull. Calcutta Math. Soc. 37, 81–89.

  • Reliability engineering, reliability theory, reliability data analysis, and modeling resource Website, www.weibull.com (retrieved on Oct 25, 2012).

  • Rikitake, T. (1976a), Earthquake prediction, Elsevier, Amsterdam, pp. 357.

  • Rikitake, T. (1976b), Recurrence of great earthquakes at subduction zones, Tectonophysics 35(4), 335–362.

    Google Scholar 

  • Rikitake, T. and Hamada, K. (2001), Earthquake prediction, In: Encyclopedia of Physical Science and Technology, 3rd Ed., Academic Press, San Diego, 4, 743–760.

  • Rinne, H. (2009), The Weibull distribution: a handbook, CRC Press, Boca Raton, FL. pp. 784.

  • Rockette, H., Antle, C., and Klimko, L. A. (1974), Maximum likelihood estimation with the Weibull model, J. Am. Stats. Assoc. 69, 246–249.

    Google Scholar 

  • Schoor, B. (1974), On the choice of the class intervals for the Chi square test of goodness of fit, J. Appl. Maths. Mech. 54(12), 249–251.

  • Schwarz, G. E. (1978), Estimating the dimension of a model, Annals Statist. 6(2), 461–464.

    Google Scholar 

  • Sharma, M. L. and Malik, S. (2006), Probabilistic seismic hazard analysis and estimation of spectral strong ground motion on bed rock in northeast India, 4th International Conference on Earthquake Engineering, Taipei, Taiwan, October 12–13, Paper no. 015.

  • Sitharam, T. G. (2008), Seismic microzonation: principles, practices and experiments. EJGE Special Volume Bouquet.

  • Smirnov, N. V. (1948), Tables for estimating the goodness of fit of empirical distributions, Annals Math. Statist. 19:279.

    Google Scholar 

  • Smith, R., L. (1985), Maximum likelihood estimation in a class of non-regular cases, Biometrika 72, 67–90.

  • SSHAC (Senior Seismic Hazard Analysis Committee), Recommendations for probabilistic seismic hazard analysis: guidance on uncertainty and use of experts (1997), US Nuclear Regulatory Commission Report, CR-6372, Washington, DC, pp. 888.

  • Sugiura, N. (1978), Further analysis of the data by Akaike’s information criterion and the finite correctness, Communication is Statistics, Theory and Methods A7, 13–26.

  • Tripathi, J. N. (2006), Probabilistic assessment of earthquake recurrence in the January 26, 2001 earthquake region of Gujarat, India, J. Seismol. 10, 119–130.

    Google Scholar 

  • Utsu, T. (1984), Estimation of parameters for recurrence models of earthquakes, Bull. Earthq. Res. Inst., Univ. of Tokyo, 59, 53–66.

  • Vere-Jones, D. (1970), Stochastic models for earthquake occurrence (with discussion), J. Royal Statist. Soc. B31, 1–62.

  • Vere-Jones, D. (1978), Earthquake prediction: a statistician’s view, J. Phys. Earth 26, 129–146.

    Google Scholar 

  • Villaverde, R. (2009), Fundamental concepts of earthquake engineering, CRC Press, 1st Ed., pp. 960.

  • Wahed, A. S., Luong, T. M., and Jeong, J. H. (2009), A New generalization of Weibull Distribution with application to a breast cancer data set, Stat. Med. 28(16), 2077–2094.

    Google Scholar 

  • Weibull, W. (1939), A statistical theory of the strength of material, Ing. Vetenskapa Acad. Handlingar 151, 1–45.

  • Weibull, W. and Sweden, S. (1951), A statistical distribution function of wide applicability, J. Appl. Mech. 18, 293–297.

    Google Scholar 

  • Wiemer, S. and Wyss, M. (2000), Minimum magnitude of complete reporting in earthquake catalogs: examples from Alaska, the Western United States, and Japan, Bull. Seismol. Soc. Am. 90, 859–869.

    Google Scholar 

  • Wikipedia, http://en.wikipedia.org/wiki/Bathtub_curve, retrieved on Oct 25, 2012.

  • Williams, C. A. (1950), On the choice of number and width of classes for the Chi square test of goodness of fit, J. Am. Statist. Assoc. 45, 77–86.

  • Woessner, J. and Wiemer, S. (2005), Assessing the quality of earthquake catalogs: estimating the magnitude of completeness and its uncertainty, Bull. Seismol. Soc. Am. 95(2), 684–698.

    Google Scholar 

  • Working Group on California Earthquake Probabilities (2003), Earthquake probabilities in the San Francisco bay region: 2002–2031 (U.S. Geologic Survey, Denver), USGS Open File Rep., p. 03–214

  • Yadav, R. B. S., Bayrak, Y., Tripathi, J. N., Chopra, S., Singh, A. P., and Bayrak, E. (2011), Probabilistic assessment of earthquake hazard parameters in NW Himalaya and the adjoining regions, Pure Appl. Geophys. 169(9), 1619–1639.

    Google Scholar 

  • Yadav, R. B. S., Bormann, P., Rastogi, B. K., Das, M. C., and Chopra, S. (2009), A homogeneous and complete earthquake catalog for northeast India and the adjoining region, Seismol. Res. Let. 80(4), 609–627.

    Google Scholar 

  • yadav, R. B. S., Tripathi, J. N., Rastogi, B. K., Das, M. C., and Chopra, S. (2010), Probabilistic assessment of earthquake recurrence in northeast India and adjoining regions, Pure Appl. Geophys. 167, 1331–1342.

  • Yazdani, A. and Kowsari, M. (2011), Statistical prediction of the sequence of large earthquakes in Iran, IJE Trans. B: Appl. 24(4), 325–336.

  • Zanakis, S. H. and Kyparisis, J. (1986), A review of maximum likelihood estimation methods for the three parameter Weibull distribution, J. Statist. Comp. and Simulation 25, 53–73.

    Google Scholar 

  • Zoller, G., Zion, Y. B., Holschneider, M., and Hainzl, S. (2007), Estimating recurrence times and seismic hazard of large earthquakes on an individual fault, Geophy. J. Int. 170, 1300–1310.

    Google Scholar 

Download references

Acknowledgments

The authors are grateful to Dr. Debasis Kundu, Professor and Head of Department of Mathematics and Statistics, Indian Institute of Technology Kanpur for his generous guidance and thorough review of the manuscript. The authors would also like to thank the two anonymous reviewers for their critical comments and technical inputs. The first author [S.P.] thankfully acknowledges the financial support from the Council of Scientific and Industrial Research (CSIR), New Delhi, India.

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Indian Institute of Technology Kanpur, 208016, Kanpur, India

    Sumanta Pasari & Onkar Dikshit

Authors
  1. Sumanta Pasari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Onkar Dikshit
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Sumanta Pasari.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pasari, S., Dikshit, O. Impact of Three-Parameter Weibull Models in Probabilistic Assessment of Earthquake Hazards. Pure Appl. Geophys. 171, 1251–1281 (2014). https://doi.org/10.1007/s00024-013-0704-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00024-013-0704-8

Keywords

Search

Navigation