Fully Localised Three-Dimensional Gravity-Capillary Solitary Waves on Water of Infinite Depth

Abstract

Fully localised three-dimensional solitary waves are steady water waves which are evanescent in every horizontal direction. Existence theories for fully localised three-dimensional solitary waves on water of finite depth have recently been published, and in this paper we establish their existence on deep water. The governing equations are reduced to a perturbation of the two-dimensional nonlinear Schrödinger equation, which admits a family of localised solutions. Two of these solutions are symmetric in both horizontal directions and an application of a suitable variant of the implicit-function theorem shows that they persist under perturbations.

1 Introduction

The classical hydrodynamic problem for waves on the surface $\{y=\eta (x,z,t)\}$ of a three-dimensional body of deep water subject to gravity and capillarity is usually expressed in terms of an Eulerian velocity potential $\varphi$ satisfying Laplace’s equation

$$\begin{aligned} \varphi _{xx} + \varphi _{yy} + \varphi _{zz} = 0, \qquad \qquad -\infty<y<\eta , \end{aligned}$$

(1.1)

the kinematic boundary conditions

$$\begin{aligned} \varphi _{y}\rightarrow & {} {0}, \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \,\, y\rightarrow -\infty , \end{aligned}$$

(1.2)

$$\begin{aligned} \eta _t= & {} \varphi _{y} - \eta _x\varphi _x - \eta _z\varphi _z, \qquad \qquad \quad y=\eta , \end{aligned}$$

(1.3)

and the dynamical boundary condition

$$\begin{aligned} \varphi _t + \frac{1}{2}(\varphi _x^2+\varphi _{y}^2+\varphi _z^2) +\eta - \left[ \frac{\eta _x}{\sqrt{1+\eta _x^2+\eta _z^2}}\right] _x - \left[ \frac{\eta _z}{\sqrt{1+\eta _x^2+\eta _z^2}}\right] _z=0, \qquad y=\eta ; \end{aligned}$$

(1.4)

here (x, y, z) are dimensionless spatial coordinates and t is time. In this paper we discuss waves of the form $\eta (x,z,t)=\eta (x-ct,z)$, $\varphi (x,y,z,t)=\varphi (x-ct,y,z)$ (propagating with permanent shape and constant speed in the x-direction) with $\eta (x-ct,z) \rightarrow 0$ as $|(x-ct,z)| \rightarrow \infty$ (decaying in every horizontal direction) and refer to them as fully localised solitary waves.

Theorem 1.1

Suppose that $c^2=2(1-\varepsilon ^2)$. For each sufficiently small value of $\varepsilon >0$ equations (1.1)–(1.4) possess two fully localised solitary-wave solutions for which $\eta \in H^3(\mathbb {R}^2)$ is symmetric in x and z, that is $\eta (-x,z)=\eta (x,z)$ and $\eta (x,-z)=\eta (x,z)$. Moreover

$$\begin{aligned} \eta (x,z)=\pm \varepsilon \zeta _0(\varepsilon x,\varepsilon z)\cos x + o(\varepsilon ) \end{aligned}$$

uniformly over $(x,z) \in \mathbb {R}^2$, where $\zeta _0$ is the unique symmetric, positive (real) solution of the two-dimensional nonlinear Schrödinger equation

$$\begin{aligned} -\tfrac{1}{2}\zeta _{xx}-\zeta _{zz} + \zeta -\tfrac{11}{16}|\zeta |^2 \zeta =0. \end{aligned}$$

(1.5)

Theorem 1.1 confirms the prediction made by formal weakly nonlinear analysis (see below) and numerical computations by Parau et al. [17] (see Fig. 1 for illustrations of typical free surfaces in their simulations). Qualitative properties of deep-water solitary waves (in two and three dimensions) have been discussed by Wheeler [23].

Fig. 1

Illustration of a symmetric fully localised solitary wave of elevation (left) and depression (right); the waves propagate in the direction shown by the arrow

We begin by introducing the Zakharov–Craig–Sulem formulation of Eqs. (1.1)–(1.4) with independent variables $\eta$ and $\Phi =\varphi |_{y=\eta }$, namely

$$\begin{aligned}&\eta _t - G(\eta )\Phi =0, \\&\Phi _t +\eta + \frac{1}{2}\Phi _x^2+ \frac{1}{2}\Phi _z^2 -\frac{(G(\eta )\Phi +\eta _x\Phi _x+\eta _z\Phi _z)^2}{2(1+\eta _x^2+\eta _z^2)} \!-\!\left[ \frac{\eta _x}{\sqrt{1+\eta _x^2+\eta _z^2}}\right] _{\!x} \!\!-\!\left[ \frac{\eta _z}{\sqrt{1+\eta _x^2+\eta _z^2}}\right] _{\!z} \!\!\!=\! 0, \end{aligned}$$

where $G(\eta )\Phi =\varphi _y -\eta _x\varphi _x-\eta _z\varphi _z\big |_{y=\eta }$ and $\varphi$ is the (unique) solution of the boundary-value problem

$$\begin{aligned}&\varphi _{xx}+\varphi _{yy}+\varphi _{zz}=0,\qquad \,\! y<\eta , \\&\varphi _y \rightarrow 0,\qquad \qquad \qquad \qquad \! y \rightarrow -\infty , \\&\varphi =\Phi ,\qquad \qquad \qquad \qquad \,\, y=\eta \end{aligned}$$

(Zakharov [24], Craig and Sulem [6]). Steady waves are nontrivial solutions of these equations of the form $\eta (x,z,t)=\eta (x-ct,z)$, $\Phi (x,z,t)=\Phi (x-ct,z)$; they satisfy

$$\begin{aligned}&-c \eta _x - G(\eta )\Phi =0, \end{aligned}$$

(1.6)

$$\begin{aligned}&-c\Phi _x +\eta + \frac{1}{2}\Phi _x^2+ \frac{1}{2}\Phi _z^2 \nonumber \\&-\frac{(G(\eta )\Phi +\eta _x\Phi _x+\eta _z\Phi _z)^2}{2(1+\eta _x^2+\eta _z^2)} -\left[ \frac{\eta _x}{\sqrt{1+\eta _x^2+\eta _z^2}}\right] _{x} -\left[ \frac{\eta _z}{\sqrt{1+\eta _x^2+\eta _z^2}}\right] _{z} = 0. \end{aligned}$$

(1.7)

Equations (1.6), (1.7) can in fact be reduced to one equation for the variable $\eta$. Equation (1.6) implies that $\Phi =-cG(\eta )^{-1}\eta _x$, whereby (1.7) yields

$$\begin{aligned} {\mathcal K}^\prime (\eta )-c^2{\mathcal L}^\prime (\eta )=0, \end{aligned}$$

(1.8)

in which

$$\begin{aligned} {\mathcal K}^\prime (\eta )&=\eta -\left[ \frac{\eta _x}{\sqrt{1+\eta _x^2+\eta _z^2}}\right] _{\!x} -\left[ \frac{\eta _z}{\sqrt{1+\eta _x^2+\eta _z^2}}\right] _{\!z}, \end{aligned}$$

(1.9)

$$\begin{aligned} {\mathcal L}^\prime (\eta )&=-\frac{1}{2}(K(\eta )\eta )^2-\frac{1}{2}(L(\eta )\eta )^2 + \frac{(\eta _x-\eta _xK(\eta )\eta -\eta _zL(\eta )\eta )^2}{2(1+\eta _x^2+\eta _z^2)} + K(\eta )\eta \end{aligned}$$

(1.10)

and

$$\begin{aligned} K(\eta )\xi = -(G(\eta )^{-1} \xi _x)_x, \qquad L(\eta )\xi = -(G(\eta )^{-1} \xi _x)_z. \end{aligned}$$

Notice that

$$\begin{aligned} K(\eta )\xi =-(\varphi |_{y=\eta })_x, \quad \;\, L(\eta )\xi =-(\varphi |_{y=\eta })_z, \end{aligned}$$

(1.11)

where $\varphi$ solves the boundary-value problem

$$\begin{aligned}&\varphi _{xx}+\varphi _{yy}+\varphi _{zz}=0,\qquad \qquad \quad \, y<\eta , \end{aligned}$$

(1.12)

$$\begin{aligned}&\varphi _y \rightarrow 0,\qquad \qquad \qquad \qquad \qquad \quad y\rightarrow -\infty , \end{aligned}$$

(1.13)

$$\begin{aligned}&\varphi _y -\eta _x\varphi _x-\eta _z\varphi _z=\xi _x,\qquad \qquad y=\eta \end{aligned}$$

(1.14)

(and is therefore unique up to an additive constant); the operators K and L are studied in Sect. 2 below. Observe that (1.8) is invariant under the reflections $\eta (x,z) \mapsto \eta (-x,z)$ and $\eta (x,z) \mapsto \eta (x,-z)$; a solution which is invariant under these transformations is termed symmetric. Although this fact is not used in the present paper, let us also note that (1.8) is in fact the Euler–Lagrange equation for the functional

$$\begin{aligned} {\mathcal J}(\eta ) := {\mathcal K}(\eta ) - c^2 {\mathcal L}(\eta ), \end{aligned}$$

in which

$$\begin{aligned} {\mathcal K}(\eta )=\int _{\mathbb {R}^2} \left( \frac{1}{2} \eta ^2 +\sqrt{1+\eta _x^2+\eta _z^2}-1\right) \, \mathrm {d}x\, \mathrm {d}z, \qquad {\mathcal L}(\eta )=\frac{1}{2}\int _{\mathbb {R}^2} \eta \, K(\eta ) \eta \, \mathrm {d}x\, \mathrm {d}z; \end{aligned}$$

the functions ${\mathcal K}^\prime$ and ${\mathcal L}^\prime$ are the $L^2(\mathbb {R}^2)$-gradients of respectively ${\mathcal K}$ and ${\mathcal L}$ (see Buffoni et al. [3, 4]).

Fig. 2

Dispersion relation for a sinusoidal wave train with wave number $k_1 > 0$ and speed $c>0$

Let us now review the formal weakly nonlinear analysis used to derive the nonlinearSchrödinger equation for steady waves (see Ablowitz and Segur [1, §2.2]), beginning with sinusoidal wave trains. The linearised version of (1.8) admits a solution of the form

$$\begin{aligned} \eta (x,z)=A \cos k_1x \end{aligned}$$

whenever $c>0$ and $k_1 > 0$ satisfy the linear dispersion relation

$$\begin{aligned} c^2 =k_1+\frac{1}{k_1} \end{aligned}$$

(see Fig. 2); note that the mapping $k_1 \mapsto c(k_1)$, $k_1 > 0$ has a unique global minimum $c_\mathrm {min}=\sqrt{2}$ at $k_1=1$. According to Dias and Kharif [7, §3] equality of the linear group and phase speeds (which occurs when $c^\prime (k_1)=0$) is associated with bifurcation of small-amplitude water waves. We therefore seek small-amplitude solitary waves with speed near $\sqrt{2}$ bifurcating from a linear sinusoidal wave train with unit wavenumber. Substituting $c^2=2(1-\varepsilon ^2)$ and the formal expansion

$$\begin{aligned}&\eta (x,z) = \tfrac{1}{2}\varepsilon \big (A_1(X,Z) \mathrm {e}^{\mathrm {i}x} + \overline{A_1(X,Z)}\mathrm {e}^{-\mathrm {i}x} \big ) \\&\quad +\varepsilon ^2 A_0(X,Z) +\tfrac{1}{2}\varepsilon ^2 \big (A_2(X,Z) \mathrm {e}^{2\mathrm {i}x} +\overline{A_2(X,Z)}\mathrm {e}^{-2\mathrm {i}x}\big ) + \cdots , \end{aligned}$$

where $X=\varepsilon x$, $Z=\varepsilon z$, into equation (1.8), one finds that $A_1$ satisfies the stationary nonlinear Schrödinger equation (1.5). This equation has a unique symmetric, positive (real) solution which is characterised as the ground state of the functional $\tilde{{\mathcal J}}: H^1(\mathbb {R}^2) \rightarrow {\mathbb {R}}$ with

$$\begin{aligned} \tilde{{\mathcal J}}(\zeta ) = \int _{\mathbb {R}^2}\left( \frac{1}{4} |\zeta _x|^2 +\frac{1}{2} |\zeta _z|^2+\frac{1}{2} |\zeta |^2 -\frac{11}{64}|\zeta |^4\right) \, \mathrm {d}x\, \mathrm {d}z\end{aligned}$$

(see Sulem and Sulem [21, §4.2] and the references therein).

Fig. 3

The support of $\hat{\eta }_1$ is contained in the set $B=B_\delta (1,0) \cup B_\delta (-1,0)$

The above Ansatz indicates that the Fourier transform $\hat{\eta }$ of the surface-profile function $\eta$ for a fully localised solitary wave is localised near the points $(\pm 1,0)$. We therefore write $\eta =\eta _1+\eta _2$, where $\mathrm {supp}(\hat{\eta }_1)$ and $\mathrm {supp}(\hat{\eta }_2)$ are contained in respectively $B=B_\delta (1,0) \cup B_\delta (-1,0)$ (with $\delta \in (0,\frac{1}{5})$) and its complement (see Fig. 3). Here the Fourier transform $\hat{\eta }={\mathcal F}[\eta ]$ of $\eta$ is defined by

$$\begin{aligned} \hat{\eta }(k)=\frac{1}{2\pi }\int _{\mathbb {R}^2}\eta (x,z)\mathrm {e}^{-\mathrm {i}(k_1x + k_3z)}\, \mathrm {d}x\, \mathrm {d}z,\qquad k=(k_1,k_3), \end{aligned}$$

and we denote the Fourier multiplier with symbol m by m(D) with $D=(-\mathrm {i}\partial _x,-\mathrm {i}\partial _z)$, so that $m(D)\eta = {\mathcal F}^{-1}[m\hat{\eta }]$; in particular $\eta _1 = \chi (D)\eta$, $\eta _2 = (1-\chi (D))\eta$, where $\chi$ is the indicator function of the set B. Writing $c^2=2(1-\varepsilon ^2)$ and equation (1.8) as

$$\begin{aligned} \chi (D)\big ({\mathcal K}^\prime (\eta _1+\eta _2)-2(1-\varepsilon ^2){\mathcal L}^\prime (\eta _1+\eta _2)\big )&=0, \\ (1-\chi (D))\big ({\mathcal K}^\prime (\eta _1+\eta _2)-2(1-\varepsilon ^2){\mathcal L}^\prime (\eta _1+\eta _2)\big )&=0, \end{aligned}$$

we find that the second equation is solvable for $\eta _2$ as a function of $\eta _1$ for sufficiently small values of $\varepsilon$; the first therefore reduces to

$$\begin{aligned} \chi (D)\big ({\mathcal K}^\prime (\eta _1+\eta _2(\eta _1))-2(1-\varepsilon ^2){\mathcal L}^\prime (\eta _1+\eta _2(\eta _1))\big )=0 \end{aligned}$$

upon inserting $\eta _2=\eta _2(\eta _1)$. Finally, the scaling

$$\begin{aligned} \eta _1(x,z) = \tfrac{1}{2}\varepsilon \zeta (X,Z) \mathrm {e}^{\mathrm {i}x} + \tfrac{1}{2}\varepsilon \overline{\zeta (X,Z)}\mathrm {e}^{-\mathrm {i}x} \end{aligned}$$

(1.15)

transforms the reduced equation into a perturbation of the equation

$$\begin{aligned} \varepsilon ^{-2}g(e+\varepsilon D)\zeta + 2f(e+\varepsilon D)\zeta - \tfrac{11}{8}|\zeta |^2\zeta =0, \end{aligned}$$

(1.16)

where $e=(1,0)$ and

$$\begin{aligned} g(s)=1+|s|^2 -2f(s),\quad f(s)=\frac{s_1^2}{|s|} \end{aligned}$$

(see Sects. 3 and 4; the reduced equation is stated precisely in equation (4.2)).

Equation (1.16) is termed a full-dispersion version of the stationary nonlinear Schrödinger equation (1.5) since it retains the linear part of the original equation (1.8); noting that

$$\begin{aligned} \varepsilon ^{-2}g(e+\varepsilon k) + 2f(e+\varepsilon k) = 2+k_1^2+2k_3^2 + O(\varepsilon ), \end{aligned}$$

we recover the fully reduced model equation in the formal limit $\varepsilon =0$ (see Obrecht and Saut [16] for a discussion of related full-dispersion model equations for three-dimensional water waves). In Sect. 5 we demonstrate that equation (1.16) for $\zeta$ has two symmetric solutions $\zeta _\varepsilon ^\pm$ which satisfy $\zeta _\varepsilon ^\pm \rightarrow \pm \zeta _0$ in $H^1(\mathbb {R}^2)$ as $\varepsilon \rightarrow 0$. The key step is a nondegeneracy result for the solution $\zeta _0$ of (1.5) (see Weinstein [22], Kwong [13] and Chang et al. [5]) in a symmetric setting which allows one to apply a suitable variant of the implicit-function theorem. For this purpose we exploit the fact that the reduction procedure preserves the invariance of equation (1.8) under $\eta (x,z) \mapsto \eta (-x,z)$ and $\eta (x,z) \mapsto \eta (x,-z)$, so that equation (1.16) is invariant under the reflections $\zeta (x,z) \mapsto \overline{\zeta (-x,z)}$ and $\zeta (x,z) \mapsto \zeta (x,-z)$.

The scaling (1.15) implies that our waves have small amplitude but finite energy. When splitting our basic function space ${\mathcal X}=H^3(\mathbb {R}^2)$ into two parts ${\mathcal X}_1=\chi (D){\mathcal X}$, ${\mathcal X}_2=(1-\chi (D)){\mathcal X}$ for $\eta _1$ and $\eta _2$, we respect this scaling by equipping ${\mathcal X}_1$ with the scaled norm $|{}|{}|\cdot |{}|{}|$ defined by

$$\begin{aligned} |{}|{}|\eta _1 |{}|{}|:=\left( \int _{\mathbb {R}^2} \big (1+\varepsilon ^{-2}\big (\big (|k_1|-1\big )^2+k_3^2\big )\big )|\hat{\eta }_1(k)|^2\, \mathrm {d}k_1 \, \mathrm {d}k_3\right) ^{1/2} =\Vert \zeta \Vert _{H^1(\mathbb {R}^2)} \end{aligned}$$

(1.17)

and taking $\zeta$ in a ball $B_R(0) \subseteq H^1(\mathbb {R}^2)$ which is large enough to contain $\zeta _0$; solving the equation for $\eta _2$ yields the estimate

$$\begin{aligned} \Vert \eta _2(\eta _1)\Vert _{H^3(\mathbb {R}^2)} \lesssim \varepsilon ^\theta |{}|{}|\eta _1 |{}|{}|^2, \end{aligned}$$

where $\theta$ is a fixed number in the interval (0, 1). Equation (1.17) shows that our waves have finite $H^3(\mathbb {R}^2)$-norm, while the estimates

$$\begin{aligned} \Vert \eta _1\Vert _\infty \lesssim \varepsilon ^\theta |{}|{}|\eta _1 |{}|{}|, \qquad \Vert \eta _2\Vert _\infty \lesssim \Vert \eta _2\Vert _{H^3(\mathbb {R}^2)}, \end{aligned}$$

show that they have small amplitude.

Comparison with previous results

The corresponding problem for water of finite depth is obtained from (1.1)–(1.4) by replacing the condition (1.2) by $\phi _y|=0$ at $y=-1$ and multiplying the terms in square brackets on the left-hand side of (1.4) by a dimensionless parameter $\beta$ (called the Bond number) measuring the strength of surface-tension effects. That problem was examined for strong capillarity ($\beta >1/3$) by Groves and Sun [9] and Buffoni et al. [3] and, more relevantly for us, for weak capillarity ($\beta <1/3$) by Buffoni et al. [4]. In the latter case one obtains a dispersion relation with a global minimum $\sqrt{\Lambda } \in (0,1)$ obtained at a unique wave number $\omega \in (0,\infty )$ depending upon $\beta$. The above weakly nonlocal analysis leads to the Davey–Stewartson equation

$$\begin{aligned} - a_1 \zeta _{xx}-a_2 \zeta _{zz} + a_3 \zeta - 2C_1 {\mathcal F}^{-1}\left[ \frac{k_1^2}{(1-\Lambda )k_1^2+k_2^2} {\mathcal F}[|\zeta |^2]\right] \zeta -2C_2|\zeta |^2\zeta =0, \end{aligned}$$

where $a_i>0$, $C_j>0$ are further constants depending on $\beta$. The Davey–Stewartson equation is the Euler–Lagrange equation for the functional

$$\begin{aligned}&\tilde{{\mathcal J}}(\zeta ) = \int _{\mathbb {R}^2}\big (a_1|\zeta _x|^2+a_2|\zeta _z|^2+a_3|\zeta |^2\big )\, \mathrm {d}x\, \mathrm {d}z\qquad \qquad \\&-C_1\int _{\mathbb {R}^2}\frac{k_1^2}{(1-\Lambda )k_1^2+k_2^2} |{\mathcal F}[|\zeta |^2]|^2\, \mathrm {d}k_1\, \mathrm {d}k_2 -C_2\int _{\mathbb {R}^2}|\zeta |^4\, \mathrm {d}x\, \mathrm {d}z. \end{aligned}$$

Buffoni et al. rigorously reduce the variational principle for fully localised three-dimensional solitary waves to a locally equivalent reduced variational principle whose variational functional is a perturbation of $\tilde{{\mathcal J}}$ and complete their existence theory by finding a nontrivial critical point of their reduced functional.

The variational method is also applicable to the infinite-depth case, but in the present paper we take a different approach, directly reducing the hydrodynamic equations themselves. The methods do however have common features, particularly in solving for $\eta _2=\eta _2(\eta _1)$ and approximating Fourier multipliers by differential operators, and for conciseness we simply state those results here and refer to reference [4] for their proofs. This direct technique was not available to Buffoni et al. since no corresponding nondegeneracy result for the Davey–Stewartson equation is currently available. However, by combining the method in the present paper with the computations in reference [4], one can obtain the existence of two families of fully localised solitary-wave solutions when $\beta >0$ is sufficiently small (which corresponds to assuming that the depth is sufficiently large in physical variables). Indeed, noting that $\omega \rightarrow \infty$ as $\beta \rightarrow 0$ and setting $\zeta (x,z)=\omega ^{-1} \tilde{\zeta }(\omega x, \omega z)$, one finds after multiplying by $\omega$ that the Davey–Stewartson equation limits to the nonlinear Schrödinger equation (1.5) for $\tilde{\zeta }$ as $\omega \rightarrow \infty$. The Davey–Stewartson equation therefore also has two families of nondegenerate fully localised solitary-wave solutions for large $\omega$. Repeating the proof of Theorem 1.1, we thus arrive at the following result.

Theorem 1.2

Fix $\beta >0$ small enough. For each sufficiently small $\varepsilon >0$ the gravity-capillary water wave problem with finite depth and $c^2=(1-\varepsilon ^2)\Lambda$ possesses two fully localised solitary-wave solutions which are symmetric in x and z.

The approach in the present paper does not use any variational arguments, relying instead upon the nondegeneracy of two particular symmetric solutions to the limiting equation (the nonlinear Schrödinger equation) to enable an application of the implicit-function theorem. It is ‘self-improving’ in that it would apply equally well to any other symmetric solution once its nondegeneracy is established; see Strauss [20], Berestycki and Lions [2], Jones and Küpper [12] and McLeod, Troy and Weissler [15] for existence theories for radial solutions to equations of nonlinear Schrödinger type (and Iaia and Warchall [11] for a discussion of nonradial solutions). By contrast, variational approaches typically require more sophisticated tools to handle multiple solutions. Our method also applies to other problems which can be reduced to a limiting equation with a nondegenerate symmetric solitary-wave solution. The limiting equation for water with finite depth and strong surface tension is the KP-I equation, which has an (explicit) symmetric solitary-wave solution. This solution has recently been shown to be nondegenerate by Liu and Wei [14], and the present method would therefore presumably lead to a simpler existence proof than the variational theory in references [9] and [3]. A similar method has also been used by Stefanov andWright [19] to establish the existence of solitary-wave solutions to a full-dispersion Korteweg–de Vries equation known as the Whitham equation.

Our method also applies to two-dimensional gravity-capillary solitary water waves, the details of which have recently been given for water of finite depth by Groves [8]. There weakly nonlocal analysis leads to the Korteweg–de Vries equation (for strong capillarity) and one-dimensional nonlinear Schrödinger equation (for weak capillarity), and both of these equations have families of explicit solitary-wave solutions. Groves follows the method developed in the present paper, showing how it can be considerably simplified in one spatial dimension, to derive perturbed full-dispersion versions of the Korteweg–de Vries and nonlinear Schrödinger equations. His analysis of the reduced equations is also simpler, since establishing the nondegeneracy of their symmetric solitary-wave solutions amounts to verifying the nondegeneracy of explicit solutions to well-known second-order ordinary differential equations. Note also that while reference [8] is an alternative approach to previously available results, the present paper gives an existence theory for a new type of wave.

Finally, let us remark that Lyapunov–Schmidt reduction in Fourier space, as carried out in Sect. 3 below, has been used by other authors in various forms (e.g. see Pelinovsky and Schneider [18] for a related reduction in a quite different setting).

2 Analyticity

In this section we sketch a proof that the operators K, L given by (1.11) and hence ${\mathcal K}^\prime$ and ${\mathcal L}^\prime$ given by (1.9), (1.10) are analytic at the origin in suitable function spaces (see Corollaries 2.2 and 2.3 below). Full details of the method are given (for different, but related mappings) by Buffoni et al. [4, §2.1].

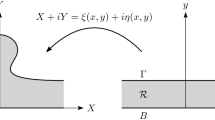
The boundary-value problem (1.12)–(1.14) can be treated by mapping the fluid domain$\Sigma _\eta =\{(x,y,z):x,z \in \mathbb {R}, -\infty< y < \eta (x,z)\}$ to the lower half-space $\Sigma =\mathbb {R}\times (-\infty ,0) \times \mathbb {R}$ using the transformation

$$\begin{aligned} y^\prime =y - \eta (x,z),\qquad u(x,y^\prime ,z)=\varphi (x,y,z). \end{aligned}$$

The equations are transformed into

$$\begin{aligned}&u_{xx}+u_{yy}+u_{zz}=\partial _x F_1(\eta ,u)+\partial _y F_2(\eta ,u)+\partial _z F_3(\eta ,u),&\quad y<0, \end{aligned}$$

(2.1)

$$\begin{aligned}&u_y \rightarrow 0,&\quad y \rightarrow - \infty , \end{aligned}$$

(2.2)

$$\begin{aligned}&u_y=F_2(\eta ,u)+\xi _x,&\quad y=0, \end{aligned}$$

(2.3)

where we have dropped the primes and defined

$$\begin{aligned} F_1(\eta ,u)=\eta _x u_y, \qquad F_2(\eta ,u)=\eta _x u_x + \eta _z u_z -(\eta _x^2+\eta _z^2) u_y, \qquad F_3(\eta ,u)=\eta _z u_y, \end{aligned}$$

so that

$$\begin{aligned} K(\eta )\xi = -u_x|_{y=0}, \qquad L(\eta )\xi =-u_z|_{y=0}. \end{aligned}$$

We study this boundary-value problem in the function space

for $\eta$ and $H^3_\star (\Sigma )$ for u, in which $H_\star ^{n+1}(\Sigma )$, $n \in {\mathbb {N}}$, is the completion of

with respect to the norm

$$\begin{aligned} \Vert u\Vert _{n+1,\star }^2 := \Vert u_x\Vert _n^2 + \Vert u_y\Vert _n^2 + \Vert u_z\Vert _n^2 \end{aligned}$$

and $\Vert \cdot \Vert _s$ denotes the usual norm for the standard Sobolev space $H^s(\mathbb {R}^2)$ or $H^s(\Sigma )$.

Lemma 2.1

For each $\xi \in H^{5/2}(\mathbb {R}^2)$ and sufficiently small $\eta \in {\mathcal Z}$ equations (2.1)–(2.3) have a unique solution $u \in H^3_\star (\Sigma )$. Furthermore, the mapping $\eta \mapsto (\xi \mapsto u)$ defines a function ${\mathcal Z}\rightarrow {\mathcal L}(H^{5/2}(\mathbb {R}^2), H^3_\star (\Sigma ))$ which is analytic at the origin.

Proof

Suppose that $F_1$, $F_2$, $F_3 \in H^2(\Sigma )$, $\xi \in H^{5/2}(\mathbb {R}^2)$ and note that the boundary-value problem

$$\begin{aligned}&u_{xx}+u_{yy}+u_{zz}=\partial _x F_1+ \partial _y F_2 +\partial _z F_3,&\quad y<0, \\&u_y \rightarrow 0,&\quad y \rightarrow - \infty , \\&u_y=F_2(\eta ,u)+\xi _x,&\quad y=0, \end{aligned}$$

has a unique solution $u=S(F_1,F_2,F_3,\xi )$ in $H^3_\star (\Sigma )$ whose gradient is obtained from the explicit formula

$$\begin{aligned} S(F_1,F_2,F_3,\xi )= & {} {\mathcal F}^{-1}\left[ \int _{-\infty }^0 \!\!\left( -\frac{\mathrm {i}k_1}{2|k|}\hat{F}_1 - \frac{\mathrm {i}k_3}{2|k|} \hat{F}_3 + \frac{1}{2}{{\,\mathrm{sgn}\,}}(y-\tilde{y}) \hat{F}_2\right) \mathrm {e}^{-|k||y-\tilde{y}|} \, \mathrm {d}\tilde{y}\right. \\&\qquad + \left. \!\!\int _{-\infty }^0 \!\!\left( -\frac{\mathrm {i}k_1}{2|k|}\hat{F}_1 - \frac{\mathrm {i}k_3}{2|k|} \hat{F}_3+\frac{1}{2}\hat{F}_2\right) \mathrm {e}^{|k|(y+\tilde{y})}\, \mathrm {d}\tilde{y}+\frac{\mathrm {i}k_1}{|k|}\hat{\xi }\mathrm {e}^{|k|y}\right] \end{aligned}$$

(with a slight abuse of notation), so that

$$\begin{aligned} \Vert S(F_1,F_2,F_3,\xi )\Vert _{3,\star } \lesssim \Vert F_1\Vert _2 + \Vert F_2\Vert _2 + \Vert F_3\Vert _2 + \Vert \xi \Vert _{5/2}. \end{aligned}$$

Define

$$\begin{aligned} T:H_\star ^3(\Sigma ) \times {\mathcal Z}\times H^{5/2}(\mathbb {R}^2) \rightarrow H_\star ^3(\Sigma ) \end{aligned}$$

by

$$\begin{aligned} T(u,\eta ,\xi )=u-S(F_1(\eta ,u),F_2(\eta ,u),F_3(\eta ,u),\xi ), \end{aligned}$$

so that zeros of $T(\cdot ,\eta ,\xi )$ correspond to solutions of (2.1)–(2.3). Using the estimates

$$\begin{aligned} \Vert \eta _x^j w\Vert _2&\le \Vert \eta _{1x}^j w\Vert _2 + \Vert \eta _{2x}^j w\Vert _2\\&\lesssim \Vert \eta _1\Vert _{3,\infty }^j \Vert w\Vert _2 + \Vert \eta _2\Vert _3^j \Vert w\Vert _2 \\&\lesssim (\Vert \hat{\eta }_1\Vert _{L^1(\mathbb {R}^2)} + \Vert \eta _2\Vert _3)^j \Vert w\Vert _2 \\&= \Vert \eta \Vert _{\mathcal Z}^j \Vert w\Vert _2, \qquad j=1,2, \end{aligned}$$

and similarly

$$\begin{aligned} \Vert \eta _z^j w\Vert _2 \lesssim \Vert \eta \Vert _{\mathcal Z}^j \Vert w\Vert _2, \qquad j=1,2 \end{aligned}$$

(where we have used the fact that $\mathrm {supp}(\hat{\eta }_1$) is compact), we find that the mappings $H_\star ^3(\Sigma ) \times {\mathcal Z}\rightarrow H^2(\Sigma )$ given by $(\eta ,u) \mapsto F_j(\eta ,u)$, $j=1,2,3$, and hence the mapping T, are analytic at the origin. Since $T(0,0,0)=0$ and $\mathrm {d}_1T[0,0,0]=I$ is an isomorphism, the analytic implicit-function theorem yields open neighbourhoods $V_1$ and $V_2$ of the origin in respectively ${\mathcal Z}$ and $H^{5/2}(\mathbb {R}^2)$ and an analytic function $v: V_1 \times V_2 \rightarrow H_\star ^3(\Sigma )$ such that

$$\begin{aligned} T(v(\eta ,\xi ),\eta ,\xi )=0. \end{aligned}$$

Since v is linear in $\xi$ we can take $V_2$ to be the entire space $H^{5/2}(\mathbb {R}^2)$. $\square$

Corollary 2.2

The mappings $K(\cdot ), L(\cdot ) :{\mathcal Z}\rightarrow {\mathcal L}(H^{5/2}(\mathbb {R}^2), H^{3/2}(\mathbb {R}^2))$ are analytic at the origin.

In view of Corollary 2.2 we choose M sufficiently small and study the equation

$$\begin{aligned} {\mathcal K}^\prime (\eta )-2(1-\varepsilon ^2){\mathcal L}^\prime (\eta )=0 \end{aligned}$$

(2.4)

in the set

$$\begin{aligned} U=\{\eta \in H^3(\mathbb {R}^2): \Vert \eta \Vert _{\mathcal Z}< M\}, \end{aligned}$$

noting that $H^3(\mathbb {R}^2)$ is continuously embedded in ${\mathcal Z}$ and that U is an open neighbourhood of the origin in $H^3(\mathbb {R}^2)$; we proceed accordingly by decomposing ${\mathcal X}=H^3(\mathbb {R}^2)$ into the direct sum of ${\mathcal X}_1=\chi (D)H^3(\mathbb {R}^2)$ and ${\mathcal X}_2=(1-\chi (D))H^3(\mathbb {R}^2)$.

Corollary 2.3

Equations (1.9), (1.10) define functions $U \rightarrow H^1(\mathbb {R}^2)$ which are analytic at the origin and satisfy ${\mathcal K}^\prime (0)={\mathcal L}^\prime (0)=0$.

Proof

The result for ${\mathcal K}^\prime$ follows from (1.9), Corollary 2.2 and the fact that $H^{3/2}(\mathbb {R}^2)$ is an algebra. The result for ${\mathcal L}^\prime$ follows from (1.10) and the observation that $\eta \mapsto \eta _x (1+\eta _x^2+\eta _z^2)^{-1/2}$ and $\eta \mapsto \eta _z (1+\eta _x^2+\eta _z^2)^{-1/2}$ define functions $U \rightarrow H^2(\mathbb {R}^2)$ which are analytic at the origin since $H^2(\mathbb {R}^2)$ is an algebra. $\square$

In keeping with Lemma 2.1 and Corollary 2.2 we write

$$\begin{aligned} u(\eta ,\xi ) = \sum _{j=0}^\infty u^j(\eta ,\xi ), \end{aligned}$$

where $u^j$ is homogeneous of degree j in $\eta$ and linear in $\xi$, and

$$\begin{aligned} K(\eta )=\sum _{j=0}^\infty K_j(\eta ), \quad L(\eta )=\sum _{j=0}^\infty L_j(\eta ), \quad {\mathcal K}^\prime (\eta ):=\sum _{j=1}^\infty {\mathcal K}^\prime _j(\eta ), \quad {\mathcal L}^\prime (\eta ):=\sum _{j=1}^\infty {\mathcal L}^\prime _j(\eta ). \end{aligned}$$

where $K_j(\eta )$, $L_j(\eta )$ and ${\mathcal K}^\prime _j(\eta )$, ${\mathcal L}^\prime _j(\eta )$ are homogeneous of degree j in $\eta$. A straightforward calculation shows that

$$\begin{aligned} u^0(\xi ) = {\mathcal F}^{-1}\left[ \frac{\mathrm {i}k_1}{|k|}\mathrm {e}^{|k|y}\hat{\xi }\right] \end{aligned}$$

and hence that $K_0$ and $L_0$ are Fourier multipliers, namely

$$\begin{aligned} K_0\xi = {\mathcal F}^{-1}\left[ \frac{k_1^2}{|k|} \hat{\xi }\right] , \qquad L_0\xi = {\mathcal F}^{-1}\left[ \frac{k_1k_3}{|k|} \hat{\xi }\right] \end{aligned}$$

(we have omitted the argument $\eta$ on the left-hand sides of these equations).

The following lemma gives expressions for the first few terms in the Taylor expansions of ${\mathcal K}^\prime (\eta )$ and ${\mathcal L}^\prime (\eta )$ at the origin; it is proved by expanding (1.9), (1.10) and examining the boundary-value problems for $u^1(\eta ,\eta )$ and $u^2(\eta ,\eta )$ to derive the formulae

$$\begin{aligned} K_1(\eta )\eta&= -(\eta \eta _x)_x-K_0(\eta K_0 \eta )-L_0(\eta L_0 \eta ), \end{aligned}$$

(2.5)

$$\begin{aligned} L_1(\eta )\eta&= -(\eta \eta _x)_z-L_0(\eta K_0 \eta )-M_0(\eta L_0 \eta ) \end{aligned}$$

(2.6)

with a similar formula for $K_2(\eta _1)\eta _1$ (see Buffoni et al. [3, pp. 1032–1033] for details in a similar setting; the restriction to $\eta _1$ is necessary to allow the use of higher-order derivatives in these expressions).

Lemma 2.4

• (i) The identities

  $$\begin{aligned} {\mathcal K}^\prime _1(\eta )&=\eta - \eta _{xx} - \eta _{zz}, \nonumber \\ {\mathcal K}^\prime _2(\eta )&=0, \nonumber \\ {\mathcal K}^\prime _3(\eta )&=\frac{1}{2} ((\eta _x^2+\eta _z^2)\eta _x)_x + \frac{1}{2}((\eta _x^2+\eta _z^2)\eta _z)_z \end{aligned}$$

  (2.7)

  hold for each $\eta \in H^3(\mathbb {R}^2)$.

• (ii) The identities

  $$\begin{aligned} {\mathcal L}^\prime _1(\eta )&= K_0\eta , \\ {\mathcal L}^\prime _2(\eta )&= \tfrac{1}{2}\left( \eta _x^2 - (K_0 \eta )^2 -(L_0 \eta )^2 -2(\eta _x\eta )_x-2K_0(\eta K_0\eta )-2L_0(\eta L_0\eta ) \right) \end{aligned}$$

  hold for each $\eta \in H^3(\mathbb {R}^2)$.

• (iii) The identity

  $$\begin{aligned} {\mathcal L}^\prime _3(\eta _1)&=K_0\eta _1\, K_0(\eta _1 K_0\eta _1) +K_0\eta _1 \,L_0 (\eta _1 L_0 \eta _1) +L_0\eta _1 \,L_0(\eta _1 K_0\eta _1)+L_0\eta _1 \, M_0(\eta _1 L_0 \eta _1)\\&\qquad \quad +K_0(\eta _1 K_0(\eta _1 K_0\eta _1)) +K_0(\eta _1 L_0 (\eta _1 L_0 \eta _1)) +L_0(\eta _1 L_0(\eta _1 K_0\eta _1))\\&\qquad \quad +L_0(\eta _1 M_0(\eta _1 L_0 \eta _1))+\eta _1 (K_0 \eta _1)\eta _{1xx}+\tfrac{1}{2}K_0(\eta _1^2\eta _{1xx}) + \tfrac{1}{2}(\eta _1^2 K_0 \eta _1)_{xx} \\&\qquad \quad +\eta _1 (L_0 \eta _1)\eta _{1xz}+\tfrac{1}{2}L_0(\eta _1^2\eta _{1xz}) + \tfrac{1}{2}(\eta _1^2 L_0 \eta _1)_{xz}, \end{aligned}$$

  where

  $$\begin{aligned} M_0\xi = {\mathcal F}^{-1}\left[ \frac{k_3^2}{|k|} \hat{\xi }\right] , \end{aligned}$$

  holds for each $\eta _1 \in {\mathcal X}_1$ and more generally for any function $\eta _1$ whose Fourier transform has compact support.

Finally, we present estimates for the cubic and higher-order parts of ${\mathcal K}^\prime (\eta )$ and ${\mathcal L}^\prime (\eta )$. The results for ${\mathcal L}^\prime (\eta )$ are established by substituting

$$\begin{aligned} K(\eta )=\sum _{j=0}^2 K_j(\eta )+K_\mathrm {c}(\eta ), \qquad L(\eta )=\sum _{j=0}^2 L_j(\eta )+L_\mathrm {c}(\eta ) \end{aligned}$$

into (1.10) and estimating the resulting formulae for ${\mathcal L}_\mathrm {c}(\eta )$ and ${\mathcal L}_\mathrm {r}(\eta )$ using the rules

$$\begin{aligned} \Vert K_j(\eta )\eta \Vert _{3/2} \lesssim \Vert \eta \Vert _{\mathcal Z}^j\Vert \eta \Vert _{5/2}, \qquad \Vert K_\mathrm {c}(\eta )\eta \Vert _{3/2} \lesssim \Vert \eta \Vert _{\mathcal Z}^3\Vert \eta \Vert _{5/2} \end{aligned}$$

(with corresponding estimates for $L_j(\eta )(\eta )$, $L_\mathrm {c}(\eta )(\eta )$ and derivatives). Since this method yields only

$$\begin{aligned} \Vert (K_1(\eta )\eta )^2\Vert _1,\ \Vert (L_1(\eta )\eta )^2\Vert _1 \lesssim \Vert \eta \Vert _{\mathcal Z}^2 \Vert \eta \Vert _3^2 \end{aligned}$$

we do not include the fourth-order terms $-\tfrac{1}{2}(K_1(\eta )\eta )^2$, $-\tfrac{1}{2}(L_1(\eta )\eta )^2$ in ${\mathcal L}^\prime _\mathrm {r}(\eta )$ and treat them separately later (see in particular Proposition 4.8).

Lemma 2.5

• (i) The quantities

  $$\begin{aligned} {\mathcal K}^\prime _\mathrm {c}(\eta ):=\sum _{j=3}^\infty {\mathcal K}^\prime _j(\eta ), \qquad {\mathcal L}^\prime _\mathrm {c}(\eta ):=\sum _{j=3}^\infty {\mathcal L}^\prime _j(\eta ) \end{aligned}$$

  satisfy the estimates

  $$\begin{aligned} \Vert {\mathcal K}^\prime _\mathrm {c}(\eta )\Vert _1\lesssim & {} \Vert \eta \Vert _{\mathcal Z}^2 \Vert \eta \Vert _3, \qquad \Vert \mathrm {d}{\mathcal K}^\prime _\mathrm {c}[\eta ](v)\Vert _1 \lesssim \Vert \eta \Vert _{\mathcal Z}^2 \Vert v\Vert _3 + \Vert \eta \Vert _{\mathcal Z}\Vert \eta \Vert _3 \Vert v\Vert _{\mathcal Z},\\ \Vert {\mathcal L}^\prime _\mathrm {c}(\eta )\Vert _1\lesssim & {} \Vert \eta \Vert _{\mathcal Z}^2 \Vert \eta \Vert _3, \qquad \Vert \mathrm {d}{\mathcal L}^\prime _\mathrm {c}[\eta ](v)\Vert _1 \lesssim \Vert \eta \Vert _{\mathcal Z}^2 \Vert v\Vert _3 + \Vert \eta \Vert _{\mathcal Z}\Vert \eta \Vert _3 \Vert v\Vert _{\mathcal Z}\end{aligned}$$

  for each $\eta \in U$ and $v \in H^2(\mathbb {R})$.

• (ii) The quantities

  $$\begin{aligned} {\mathcal K}^\prime _\mathrm {r}(\eta ):=\sum _{j=4}^\infty {\mathcal K}^\prime _j(\eta ), \qquad {\mathcal L}^\prime _\mathrm {r}(\eta ):=\sum _{j=4}^\infty {\mathcal L}^\prime _j(\eta )+\tfrac{1}{2}(K_1(\eta )\eta )^2+\tfrac{1}{2}(L_1(\eta )\eta )^2 \end{aligned}$$

  satisfy the estimates

  $$\begin{aligned} \Vert {\mathcal K}^\prime _\mathrm {r}(\eta )\Vert _1\lesssim & {} \Vert \eta \Vert _{{\mathcal Z}}^4 \Vert \eta \Vert _3, \qquad \Vert \mathrm {d}{\mathcal K}^\prime _\mathrm {r}[\eta ](v)\Vert _1 \lesssim \Vert \eta \Vert _{{\mathcal Z}}^4 \Vert v\Vert _3 + \Vert \eta \Vert _{{\mathcal Z}}^3 \Vert \eta \Vert _3\Vert v\Vert _{\mathcal Z},\\ \Vert {\mathcal L}^\prime _\mathrm {r}(\eta )\Vert _1\lesssim & {} \Vert \eta \Vert _{{\mathcal Z}}^3 \Vert \eta \Vert _3, \qquad \Vert \mathrm {d}{\mathcal L}^\prime _\mathrm {r}[\eta ](v)\Vert _1 \lesssim \Vert \eta \Vert _{{\mathcal Z}}^3 \Vert v\Vert _3 + \Vert \eta \Vert _{{\mathcal Z}}^2 \Vert \eta \Vert _3\Vert v\Vert _{\mathcal Z}\end{aligned}$$

  for each $\eta \in U$ and $v \in H^2(\mathbb {R})$.

3 Reduction

Observe that $\eta \in U$ satisfies (2.4) if and only if

$$\begin{aligned} \eta _1-\eta _{1xx}-\eta _{1zz}-2 K_0\eta _1 +2\varepsilon ^2K_0\eta _1+\chi (D){\mathcal N}(\eta _1+\eta _2)&=0, \end{aligned}$$

(3.1)

$$\begin{aligned} \eta _2-\eta _{2xx}-\eta _{2zz}-2 K_0\eta _2 +2\varepsilon ^2 K_0\eta _2+(1-\chi (D)){\mathcal N}(\eta _1+\eta _2)&=0, \end{aligned}$$

(3.2)

in which

$$\begin{aligned} {\mathcal N}(\eta )={\mathcal K}^\prime _\mathrm {c}(\eta )-2(1-\varepsilon ^2)\big ({\mathcal L}^\prime _2(\eta )+{\mathcal L}^\prime _\mathrm {c}(\eta )\big ). \end{aligned}$$

The nonlinearity in (3.1) is at leading order cubic in $\eta _1$ because $\chi (D){\mathcal L}^\prime _2(\eta _1)$ vanishes; we therefore write it as

$$\begin{aligned} \eta _1-\eta _{1xx}-\eta _{1zz}-2 K_0\eta _1 +2\varepsilon ^2K_0\eta _1+\chi (D)\left( {\mathcal N}(\eta _1+\eta _2)+2(1-\varepsilon ^2){\mathcal L}^\prime _2(\eta _1)\right) =0 \end{aligned}$$

(3.3)

and make the corresponding adjustment to (3.2), that is ‘replacing’ its nonlinearity with

$$\begin{aligned} (1-\chi (D))\left( {\mathcal N}(\eta _1+\eta _2)+2(1-\varepsilon ^2){\mathcal L}^\prime _2(\eta _1)\right) , \end{aligned}$$

by writing

$$\begin{aligned} \eta _2 = F(\eta _1)+\eta _3, \qquad F(\eta _1):= 2(1-\varepsilon ^2){\mathcal F}^{-1}\left[ \frac{1-\chi (k)}{g(k)}{\mathcal F}[{\mathcal L}^\prime _2(\eta _1)]\right] \end{aligned}$$

(with the requirement that $\eta _1+F(\eta _1)+\eta _3 \in U$). Equation (3.2) may thus be cast in the form

$$\begin{aligned} \eta _3 = -{\mathcal F}^{-1}\Bigg [\frac{1-\chi (k)}{g(k)}{\mathcal F}\Big [2(1-\varepsilon ^2){\mathcal L}^\prime _2(\eta _1) +{\mathcal N}(\eta _1+F(\eta _1)+\eta _3)+2\varepsilon ^2 K_0(F(\eta _1)+\eta _3)\Big ]\Bigg ], \end{aligned}$$

(3.4)

where

$$\begin{aligned} g(k)=1+|k|^2-2\frac{k_1^2}{|k|} \ge 0 \end{aligned}$$

with equality if and only if $k=\pm (1,0)$. The following result follows from the fact that$g(k) > rsim 1+|k|^2$ for $|k| -1 \ge \delta$.

Proposition 3.1

The mapping

$$f\mapsto {\mathcal F}^{-1}\left[ \frac{1-\chi (k)}{g(k)}\hat{f}\right] $$

defines a bounded linear operator $H^1(\mathbb {R}^2)\rightarrow H^3(\mathbb {R}^2)$.

We proceed by solving (3.4) for $\eta _3$ as a function of $\eta _1$ using a straightforward extension of the standard Banach fixed-point theorem.

Theorem 3.2

Let ${\mathcal X}_1$, ${\mathcal X}_2$ be Banach spaces, $X_1$, $X_2$ be closed, convex sets in, respectively, ${\mathcal X}_1$, ${\mathcal X}_2$ containing the origin and ${\mathcal G}:X_1\times X_2 \rightarrow {\mathcal X}_2$ be a smooth mapping. Suppose there exists a continuous mapping $r:X_1\rightarrow [0,\infty )$ such that

$$\begin{aligned} \Vert {\mathcal G}(x_1,0)\Vert \le \tfrac{1}{2}r, \quad \Vert \mathrm {d}_2 {\mathcal G}[x_1,x_2]\Vert \le \tfrac{1}{3} \end{aligned}$$

for each $x_2\in \overline{B}_r(0)\subseteq X_2$ and each $x_1\in X_1$.

Under these hypotheses there exists for each $x_1\in X_1$ a unique solution $x_2=x_2(x_1)$ of the fixed-point equation $x_2={\mathcal G}(x_1,x_2)$ satisfying $x_2(x_1)\in \overline{B}_r(0)$. Moreover $x_2(x_1)$ is a smooth function of $x_1\in X_1$ with

$$\begin{aligned} \Vert \mathrm {d} x_2[x_1]\Vert \le 2\Vert \mathrm {d}_1 {\mathcal G}[x_1, x_2(x_1)]\Vert . \end{aligned}$$

We apply Theorem 3.2 to equation (3.4) with ${\mathcal X}_1=\chi (D)H^3(\mathbb {R}^2)$, ${\mathcal X}_2=(1-\chi (D))H^3(\mathbb {R}^2)$, equipping ${\mathcal X}_1$ with the scaled norm

$$\begin{aligned} |{}|{}|\eta |{}|{}|:=\left( \int _{\mathbb {R}^2} \left( 1+\varepsilon ^{-2}((|k_1|-1)^2+k_3^2)\right) |\hat{\eta }(k)|^2\, \mathrm {d}k_1 \, \mathrm {d}k_3\right) ^{\!1/2} \end{aligned}$$

and ${\mathcal X}_2$ with the usual norm for $H^3(\mathbb {R}^2)$, taking

$$\begin{aligned} X_1=\{\eta _1\in {\mathcal X}_1 :|{}|{}|\eta _1|{}|{}|\le R_1\}, \qquad X_3=\{\eta _3\in {\mathcal X}_2 :\Vert \eta _3\Vert _3 \le R_3\} \end{aligned}$$

and defining ${\mathcal G}$ as the right-hand side of (3.4). (We have written $X_3$ in place of $X_2$ for notational consistency.) The calculation

$$\begin{aligned} \int _{\mathbb {R}^2} |\hat{\eta }_1(k)|\, \mathrm {d}k_1\, \mathrm {d}k_3&= \int _{\mathbb {R}^2}\frac{(1+\varepsilon ^{-2}((|k_1|-1)^2+k_3^2))^{1/2}}{(1+\varepsilon ^{-2}((|k_1|-1)^2+k_3^2))^{1/2}} |\hat{\eta }_1(k)| \, \mathrm {d}k_1 \, \mathrm {d}k_3\\&\le 2|{}|{}|\eta |{}|{}|\left( \int _{B_\delta (1,0)} \frac{1}{1+\varepsilon ^{-2}((k_1-1)^2+k_3^2)} \, \mathrm {d}k_1 \, \mathrm {d}k_3 \right) ^{1/2} \\&= 2\sqrt{\pi }\varepsilon (\log (1+\delta ^2\varepsilon ^{-2}))^{1/2} |{}|{}|\eta |{}|{}|\end{aligned}$$

shows that

$$\begin{aligned} \Vert \hat{\eta }_1\Vert _{L^1(\mathbb {R}^2)} \lesssim \varepsilon ^\theta |{}|{}|\eta _1 |{}|{}|, \qquad \eta _1 \in {\mathcal X}_1, \end{aligned}$$

(3.5)

for each fixed $\theta \in (0,1)$. In most of our theory the value of the constant $\theta$ is irrelevant; however it will later be given the concrete value $\theta =5/6$. One can therefore ensure that $\Vert \hat{\eta }_1\Vert _{L^1(\mathbb {R}^2)} < M/2$ for all $\eta _1 \in X_1$ for any (large) value of $R_1$, while the value of $R_3$ is limited by the condition that $\Vert F(\eta _1) + \eta _3\Vert _3 < M/2$ for all $\eta _1 \in X_1$ and $\eta _3 \in X_3$, so that $\eta _1+F(\eta _1)+\eta _3 \in U$ (Corollary 3.4 below shows that $\Vert F(\eta _1)\Vert _3 = O(\varepsilon ^\theta )$ uniformly over $\eta _1 \in X_1$).

We proceed by estimating each term in the formula for ${\mathcal G}$, using the inequalities

$$\begin{aligned} \Vert \eta \Vert _\infty \lesssim \Vert \eta \Vert _{\mathcal Z}, \quad \Vert \eta \Vert _{\mathcal Z}\lesssim \varepsilon ^\theta |{}|{}|\eta _1 |{}|{}|+ \Vert \eta _3\Vert _3, \quad \Vert \eta \Vert _3 \lesssim |{}|{}|\eta _1 |{}|{}|+ \Vert \eta _3\Vert _3 \end{aligned}$$

and making extensive use of the fact that $\mathrm {supp}(\hat{\eta }_1)$ is contained in the fixed bounded set B, so that for example

$$\begin{aligned} \Vert \eta _1\Vert _n \lesssim \Vert \eta _1\Vert _0, \qquad \Vert \eta _1\Vert _{n,\infty } \lesssim \varepsilon ^\theta |{}|{}|\eta _1 |{}|{}|\end{aligned}$$

for each $n \in {\mathbb {N}}_0$.

To estimate $F(\eta _1)$ we write ${\mathcal L}^\prime _2(\eta )=m(\eta ,\eta )$ with

$$\begin{aligned} m(u,v)&=\tfrac{1}{2}\left( u_x v_x - (K_0 u) (K_0 v) -(L_0 u) (L_0 v) \right) \nonumber \\&\qquad +\tfrac{1}{2}\left( -(u_xv +u v_x)_x-K_0(u K_0 v+v K_0 u)-L_0(u L_0v +vL_0u) \right) \end{aligned}$$

(3.6)

(see Lemma 2.4(ii)), and observe that

$$\begin{aligned} \mathrm {d}{\mathcal L}^\prime _2[\eta ](v)=2m(\eta ,v). \end{aligned}$$

The proof of the following proposition is given (for a related mapping) by Buffoni et al. [4, Proposition 5].

Proposition 3.3

The estimate

$$\begin{aligned} \Vert m(u,v)\Vert _1 \lesssim \Vert u\Vert _{\mathcal Z}\Vert v\Vert _3 \end{aligned}$$

holds for each u, $v\in H^3(\mathbb {R}^2)$.

Corollary 3.4

The estimates

$$\begin{aligned} \Vert F(\eta _1)\Vert _3\lesssim \varepsilon ^\theta |{}|{}|\eta _1|{}|{}|^2,\quad \Vert \mathrm {d}F[\eta _1]\Vert _{{\mathcal L}({\mathcal X}_1, {\mathcal X}_2)} \lesssim \varepsilon ^\theta |{}|{}|\eta _1|{}|{}|\end{aligned}$$

hold for each $\eta _1\in X_1$.

Remark 3.5

Noting that

$$\begin{aligned} K_0 F(\eta _1) = 2(1-\varepsilon ^2){\mathcal F}^{-1}\left[ \frac{1-\chi (k)}{g(k)} \frac{k_1^2}{|k|} {\mathcal F}[{\mathcal L}^\prime _2(\eta _1)]\right] \end{aligned}$$

and that $\mathrm {supp}({\mathcal F}[{\mathcal L}^\prime _2(\eta _1)])$ is compact, one finds that $K_0 F(\eta _1)$ satisfies the same estimates as $F(\eta _1)$.

Lemma 3.6

The quantity

$$\begin{aligned} {\mathcal N}_1(\eta _1,\eta _3) = {\mathcal L}^\prime _2(\eta _1+F(\eta _1)+\eta _3)-{\mathcal L}^\prime _2(\eta _1) \end{aligned}$$

satisfies the estimates

• (i) $\Vert {\mathcal N}_1(\eta _1,\eta _3)\Vert _1\lesssim \varepsilon ^{2\theta } |{}|{}|\eta _1|{}|{}|^3+\varepsilon ^\theta |{}|{}|\eta _1|{}|{}|^2\Vert \eta _3\Vert _3 +\varepsilon ^\theta |{}|{}|\eta _1|{}|{}|\Vert \eta _3\Vert _3+\Vert \eta _3\Vert _3^2$,

• (ii) $\Vert \mathrm {d}_1{\mathcal N}_1[\eta _1,\eta _3]\Vert _{{\mathcal L}({\mathcal X}_1,H^1(\mathbb {R}^2))}\lesssim \varepsilon ^{2\theta } |{}|{}|\eta _1|{}|{}|^2 +\varepsilon ^\theta |{}|{}|\eta _1|{}|{}|\Vert \eta _3\Vert _3+\varepsilon ^\theta \Vert \eta _3\Vert _3$,

• (iii) $\Vert \mathrm {d}_2{\mathcal N}_1[\eta _1,\eta _3]\Vert _{{\mathcal L}({\mathcal X}_2,H^1(\mathbb {R}^2))}\lesssim \varepsilon ^\theta |{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3$

for each $\eta _1\in X_1$ and $\eta _3\in X_3$.

Proof

We estimate

$$\begin{aligned} {\mathcal N}_1(\eta _1,\eta _3) = 2m(\eta _1, F(\eta _1)+\eta _3)+m(F(\eta _1)+\eta _3,F(\eta _1)+\eta _3) \end{aligned}$$

by combining Proposition 3.3 with Corollary 3.4 using the chain rule. $\square$

Lemma 3.7

The quantity

$$\begin{aligned} {\mathcal N}_2(\eta _1,\eta _3)={\mathcal K}^\prime _\mathrm {c}(\eta _1+F(\eta _1)+\eta _3)-2(1-\varepsilon ^2){\mathcal L}^\prime _\mathrm {c}(\eta _1+F(\eta _1)+\eta _3), \end{aligned}$$

satisfies the estimates

• (i) $\Vert {\mathcal N}_2(\eta _1,\eta _3)\Vert _1\lesssim (\varepsilon ^\theta |{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3)^2(|{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3)$,

• (ii) $\Vert \mathrm {d}_1{\mathcal N}_2[\eta _1,\eta _3]\Vert _{{\mathcal L}({\mathcal X}_1,H^1(\mathbb {R}^2))} \lesssim (\varepsilon ^\theta |{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3)^2$,

• (iii) $\Vert \mathrm {d}_2{\mathcal N}_2[\eta _1,\eta _3]\Vert _{{\mathcal L}({\mathcal X}_2,H^1(\mathbb {R}^2))}\lesssim (\varepsilon ^{\theta }|{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3)(|{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3)$

for each $\eta _1\in X_1$ and $\eta _3\in X_3$.

Proof

We compute the derivatives of ${\mathcal N}_2$ using the chain rule and estimate these expressions using the linearity of the derivative, Lemma 2.5(i) and Corollary 3.4. $\square$

Altogether the above results establish the following estimates for ${\mathcal G}$ (see Proposition 3.1, Remark 3.5 and Lemmata 3.6, 3.7).

Lemma 3.8

The function ${\mathcal G}: X_1 \times X_3 \rightarrow {\mathcal X}_2$ satisfies the estimates

• (i) $\Vert {\mathcal G}(\eta _1,\eta _3)\Vert _3\lesssim (\varepsilon ^\theta |{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3)^2(1+|{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3)+\varepsilon ^2\Vert \eta _3\Vert _3$,

• (ii) $\Vert \mathrm {d}_1{\mathcal G}[\eta _1,\eta _3]\Vert _{{\mathcal L}({\mathcal X}_1,{\mathcal X}_2)} \lesssim (\varepsilon ^\theta |{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3) (\varepsilon ^\theta +\varepsilon ^\theta |{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3)$,

• (iii) $\Vert \mathrm {d}_2{\mathcal G}[\eta _1,\eta _3]\Vert _{{\mathcal L}({\mathcal X}_2)}\lesssim (\varepsilon ^{\theta }|{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3)(1+|{}|{}|\eta _1|{}|{}|+\Vert \eta _3\Vert _3)+\varepsilon ^2$

for each $\eta _1\in X_1$ and $\eta _3\in X_3$.

Theorem 3.9

Equation (3.4) has a unique solution $\eta _3 \in X_3$ which depends smoothly upon $\eta _1 \in X_1$ and satisfies the estimates

$$\begin{aligned} \Vert \eta _3(\eta _1)\Vert _3 \lesssim \varepsilon ^{2\theta } |{}|{}|\eta _1|{}|{}|^2, \qquad \Vert \mathrm {d}\eta _3[\eta _1]\Vert _{{\mathcal L}({\mathcal X}_1,{\mathcal X}_2)} \lesssim \varepsilon ^{2\theta } |{}|{}|\eta _1|{}|{}|. \end{aligned}$$

Proof

Choosing $R_3$ and $\varepsilon$ sufficiently small, $\sigma >0$ sufficiently large and setting $r(\eta _1)=\sigma \varepsilon ^{2\theta } |{}|{}|\eta _1 |{}|{}|^2$, one finds that

$$\begin{aligned}\Vert {\mathcal G}(\eta _1,0)\Vert _3 \le \tfrac{1}{2}r(\eta _1), \qquad \Vert \mathrm {d}_2 {\mathcal G}[\eta _1,\eta _3]\Vert _{{\mathcal L}({\mathcal X}_2)} \lesssim \varepsilon ^{\theta } \end{aligned}$$

for $\eta _1 \in X_1$ and $\eta _3 \in \overline{B}_{r(\eta _1)}(0) \subset X_3$ (Lemma 3.8(i), (iii)). According to Theorem 3.2 equation (3.4) has a unique solution $\eta _3$ in $\overline{B}_{r(\eta _1)}(0) \subset X_3$ depending smoothly upon $\eta _1 \in X_1$ whose derivative is estimated using Lemma 3.8(ii). $\square$

The reduced equation

$$\begin{aligned} \eta _1-\eta _{1xx}&-\eta _{1zz}-2 K_0\eta _1 \nonumber \\&+2\varepsilon ^2K_0\eta _1+\chi (D)\left( {\mathcal N}(\eta _1+F(\eta _1)+\eta _3(\eta _2))+2(1-\varepsilon ^2){\mathcal L}^\prime _2(\eta _1)\right) =0 \end{aligned}$$

(3.7)

for $\eta _1 \in X_1$ is obtained by substituting $\eta _2=\eta _1+F(\eta _1)+\eta _3(\eta _1)$ into (3.3). Observe that (3.7) is invariant under the reflections $\eta _1(x,z) \mapsto \eta _1(-x,z)$ and $\eta _1(x,z) \mapsto \eta _1(x,-z)$; a familiar argument shows that they are inherited from the corresponding invariance of (3.3), (3.4) under $\eta _1(x,z) \mapsto \eta _1(-x,z)$, $\eta _3(x,z) \mapsto \eta _3(-x,z)$ and $\eta _1(x,z) \mapsto \eta _1(x,-z)$, $\eta _3(x,z) \mapsto \eta _3(x,-z)$ when applying Theorem 3.2.

4 Derivation of the reduced equation

Writing

$$\begin{aligned} \eta _1 = \eta _1^+ + \eta _1^-, \end{aligned}$$

where $\eta _1^+=\chi ^+(D)\eta _1$, $\eta _1^-=\chi ^-(D)\eta _1$ and $\chi ^+$, $\chi ^-$ are the indicator functions of respectively $B_\delta (1,0)$ and $B_\delta (-1,0)$ in (3.7), we find that $\eta _1^+$ satisfies the equation

$$\begin{aligned} \eta _1^+-\eta _{1xx}^+&-\eta _{1zz}^+-2 K_0\eta _1^+ \nonumber \\&+2\varepsilon ^2K_0\eta ^+_1+\chi ^+(D)\left( {\mathcal N}(\eta _1+F(\eta _1)+\eta _3(\eta _2))+2(1-\varepsilon ^2){\mathcal L}^\prime _2(\eta _1)\right) =0 \end{aligned}$$

(4.1)

(and $\eta _1^-$ satisfies its complex conjugate). The next step is to calculate the cubic terms in equation (4.1) explicitly; we employ the following notation for the higher-order terms.

Definition 4.1

• (i) The symbol $\underline{O}(\varepsilon ^\gamma |{}|{}|\eta _1 |{}|{}|^r)$ denotes a smooth function $N: X_1 \rightarrow H^1(\mathbb {R}^2)$ with

  $$\begin{aligned} \Vert N(\eta _1)\Vert _1 \lesssim \varepsilon ^\gamma |{}|{}|\eta _1 |{}|{}|^r, \qquad \Vert \mathrm {d}N[\eta _1]\Vert _{{\mathcal L}({\mathcal X}_1, H^1(\mathbb {R}^2))}\lesssim \varepsilon ^\gamma |{}|{}|\eta _1 |{}|{}|^{r-1} \end{aligned}$$

  for each $\eta _1 \in X_1$ (where $\gamma \ge 0$, $r \ge 1$). Furthermore

  $$\begin{aligned} \underline{O}_0(\varepsilon ^\gamma |{}|{}|\eta _1 |{}|{}|^r):=\chi _0(D)\underline{O}(\varepsilon ^\gamma |{}|{}|\eta _1 |{}|{}|^r), \qquad \underline{O}_+(\varepsilon ^\gamma |{}|{}|\eta _1 |{}|{}|^r) := \chi ^+(D)\underline{O}(\varepsilon ^\gamma |{}|{}|\eta _1 |{}|{}|^r), \end{aligned}$$

  where $\chi _0$, $\chi ^+$ are the indicator functions of respectively $B_\delta (0,0)$ and $B_\delta (1,0)$.

• (ii) The symbol $\underline{O}^\varepsilon _n(\Vert u \Vert _1^r)$ denotes $\chi _0(\varepsilon D)N(u)$, where N is a smooth function$B_R(0) \subseteq \chi _0(\varepsilon D)H^1(\mathbb {R}^2) \rightarrow H^n(\mathbb {R}^2)$ or $B_R(0) \subseteq H^1(\mathbb {R}^2) \rightarrow H^n(\mathbb {R}^2)$ with

  $$\begin{aligned} \Vert N(u)\Vert _n \lesssim \Vert u \Vert _1^r, \qquad \Vert \mathrm {d}N[u]\Vert _{{\mathcal L}(H^1(\mathbb {R}^2),H^n(\mathbb {R}^2))}\lesssim \Vert u \Vert _1^{r-1} \end{aligned}$$

  for each $u \in B_R(0)$ (with $r \ge 1$, $n \ge 0$).

A Fourier multiplier m(D) may be approximated by $m(\omega ,0)$ when acting upon a function whose Fourier transform is supported near the point $(\omega ,0)$. The proof of the following lemma is given by Buffoni et al. [4, Lemma 11] (in a slightly different context).

Lemma 4.2

The estimates

• (i) $\partial _x \eta _1^\pm = \pm \mathrm {i}\eta _1^\pm + \underline{O}(\varepsilon |{}|{}|\eta _1|{}|{}|)$,

• (ii) $\partial _x^2 \eta _1^\pm =-\eta _1^\pm + \underline{O}(\varepsilon |{}|{}|\eta _1|{}|{}|)$,

• (iii) $\partial _z \eta _1^\pm = \underline{O}(\varepsilon |{}|{}|\eta _1|{}|{}|)$,

• (iv) $K_0 \eta _1^\pm = \eta _1^\pm + \underline{O}(\varepsilon |{}|{}|\eta _1|{}|{}|)$,

• (v) $L_0 \eta _1^\pm = \underline{O}(\varepsilon |{}|{}|\eta _1|{}|{}|)$,

• (vi) $K_0((\eta _1^\pm )^2) = 2(\eta _1^\pm )^2 + \underline{O}(\varepsilon ^{1+\theta }|{}|{}|\eta _1|{}|{}|^2)$,

• (vii) $L_0((\eta _1^\pm )^2) = \underline{O}(\varepsilon ^{1+\theta }|{}|{}|\eta _1|{}|{}|^2)$,

• (viii) $K_0 (\eta _1^+ \eta _1^-) = \underline{O}(\varepsilon ^{1+\theta }|{}|{}|\eta _1|{}|{}|^2)$,

• (ix) $L_0 (\eta _1^+ \eta _1^-) = \underline{O}(\varepsilon ^{1+\theta }|{}|{}|\eta _1|{}|{}|^2)$,

• (x) ${\mathcal F}^{-1}[g(k)^{-1}{\mathcal F}[(\eta _1^\pm )^2]]=(\eta _1^\pm )^2+ \underline{O}(\varepsilon ^{1+\theta }|{}|{}|\eta _1|{}|{}|^2)$,

• (xi) $K_0(\eta _1^-(\eta _1^+)^2) = \eta _1^-(\eta _1^+)^2 +\underline{O}(\varepsilon ^{1+2\theta }|{}|{}|\eta _1|{}|{}|^3)$

hold for each $\eta _1 \in X_1$.

We proceed by approximating each term in the nonlinearity on the right-hand side of (4.1) according to the rules given in Lemma 4.2.

Proposition 4.3

The estimate

$$\begin{aligned} F(\eta _1)=-2\left( (\eta _1^+)^2+(\eta _1^-)^2\right) +F_\mathrm {r}(\eta _1),\qquad F_\mathrm {r}(\eta _1)= \underline{O}(\varepsilon ^{1+\theta }|{}|{}|\eta _1|{}|{}|^2) \end{aligned}$$

holds for each $\eta _1 \in X_1$.

Proof

Using the expansions given in Lemma 4.2, we find that

$$\begin{aligned} {\mathcal L}^\prime _2(\eta _1)=m(\eta _1,\eta _1)=-\left( (\eta _1^+)^2+(\eta _1^-)^2\right) +\underline{O}(\varepsilon ^{1+\theta }|{}|{}|\eta _1|{}|{}|^2). \end{aligned}$$

It follows that

$$\begin{aligned} {\mathcal F}^{-1}\left[ \frac{1-\chi (k)}{g(k)}{\mathcal F}[{\mathcal L}^\prime _2(\eta _1)]\right] = - \left( (\eta _1^+)^2+(\eta _1^-)^2\right) +\underline{O}(\varepsilon ^{1+\theta }|{}|{}|\eta _1|{}|{}|^2) \end{aligned}$$

because of Lemma 4.2(x) and the fact that

$$\begin{aligned} {\mathcal F}^{-1}\left[ \frac{1-\chi (k)}{g(k)}{\mathcal F}[\underline{O}(\varepsilon ^{1+\theta } |{}|{}|\eta _1|{}|{}|^2)]\right] = \underline{O}(\varepsilon ^{1+\theta } |{}|{}|\eta _1|{}|{}|^2) \end{aligned}$$

(because $(1-\chi (k))g(k)^{-1}$ is bounded). We conclude that

$$\begin{aligned} F(\eta _1) = 2(1-\varepsilon ^2){\mathcal F}^{-1}\left[ \frac{1-\chi (k)}{g(k)}{\mathcal F}[{\mathcal L}^\prime _2(\eta _1)]\right] = -2\left( (\eta _1^+)^2+(\eta _1^-)^2\right) +\underline{O}(\varepsilon ^{1+\theta }|{}|{}|\eta _1|{}|{}|^2).\qquad \qquad {\Box } \end{aligned}$$

Remark 4.4

The remainder term $F_\mathrm {r}(\eta _1)$ in the formula for $F(\eta _1)$ given in Proposition 4.3 satisfies

$$\begin{aligned} \Vert F_\mathrm {r}(\eta _1)\Vert _n \lesssim \varepsilon ^{1+\theta } |{}|{}|\eta _1 |{}|{}|^2, \qquad \Vert \mathrm {d}F_\mathrm {r}[\eta _1]\Vert _{{\mathcal L}({\mathcal X}_1, H^n(\mathbb {R}^2))}\lesssim \varepsilon ^{1+\theta } |{}|{}|\eta _1 |{}|{}|\end{aligned}$$

for all $n \in \mathbb {N}_0$ since its Fourier transform is supported in the region $B+B$.

Proposition 4.5

The estimate

$$\begin{aligned} \chi ^+(D){\mathcal N}_1(\eta _1,\eta _3(\eta _1))= 4\chi ^+(D)\big (\eta _1^-(\eta _1^+)^2\big ) + \underline{O}_+(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^3) \end{aligned}$$

holds for each $\eta _1 \in X_1$.

Proof

Observe that

$$\begin{aligned} \chi ^+(D){\mathcal N}_1(\eta _1,\eta _3(\eta _1))&=\chi ^+(D)\big (2m(\eta _1,F(\eta _1)+\eta _3)+m(F(\eta _1)+\eta _3,F(\eta _1)+\eta _3)\big ) \\&= 2\chi ^+(D)m(\eta _1,F(\eta _1))+ \underline{O}(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^3), \end{aligned}$$

in which we have used the calculations

$$\begin{aligned} m(\eta _1,\eta _3) =\underline{O}(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^3), \qquad m(F(\eta _1),\eta _3) = \underline{O}(\varepsilon ^{3\theta } |{}|{}|\eta _1 |{}|{}|^4) \end{aligned}$$

(see Proposition 3.3, Corollary 3.4 and Theorem 3.9) and

$$\begin{aligned} m(F(\eta _1),F(\eta _1)) = \underline{O}(\varepsilon ^{3\theta } |{}|{}|\eta _1 |{}|{}|^4) \end{aligned}$$

(because of (3.6) and Proposition 4.3). Observing that

$$\begin{aligned} m(\eta _1,F_\mathrm {r}(\eta _1)) = \underline{O}(\varepsilon ^{1+2\theta }|{}|{}|\eta _1 |{}|{}|^3) \end{aligned}$$

(see Proposition 3.3 and Remark 4.4), we find that

$$\begin{aligned} \chi ^+(D)m(\eta _1,F(\eta _1))=-2\chi ^+(D)m(\eta _1^-,(\eta _1^+)^2)+\underline{O}_+(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^3), \end{aligned}$$

and it follows from (3.6) and Lemma 4.2 that

$$\begin{aligned} m(\eta _1^-,(\eta _1^+)^2) =-\eta _1^-(\eta _1^+)^2 + \underline{O}(\varepsilon ^{3\theta } |{}|{}|\eta _1 |{}|{}|^3).{\Box } \end{aligned}$$

$\square$

Proposition 4.6

The estimates

$$\begin{aligned} \chi ^+(D){\mathcal K}^\prime _3(\eta _1+F(\eta _1) + \eta _3(\eta _1))&= -\tfrac{3}{2}\chi ^+(D)\big (\eta _1^-(\eta _1^+)^2\big )+\underline{O}_+(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^3), \\ \chi ^+(D){\mathcal L}^\prime _3(\eta _1+F(\eta _1) + \eta _3(\eta _1))&= -2\chi ^+(D)\big (\eta _1^-(\eta _1^+)^2\big )+\underline{O}_+(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^3) \end{aligned}$$

hold for each $\eta _1 \in X_1$.

Proof

Using the estimates for $F(\eta _1)$ and $\eta _3(\eta _1)$ given in Corollary 3.4 and Theorem 3.9, we find that

$$\begin{aligned} {\mathcal K}^\prime _3(\eta _1+F(\eta _1) + \eta _3(\eta _1)) ={\mathcal K}^\prime _3(\eta _1)+\underline{O}(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^4) \end{aligned}$$

and

$$\begin{aligned} \chi ^+(D){\mathcal K}^\prime _3(\eta _1)=-\tfrac{3}{2}\chi ^+(D)\big (\eta _1^-(\eta _1^+)^2\big )+\underline{O}_+(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^3)) \end{aligned}$$

(because of equation (2.7)). It similarly follows from the formula

$$\begin{aligned} {\mathcal L}^\prime _3(\eta )= - K_0\eta K_1(\eta )\eta - L_0 \eta L_1(\eta )\eta - \eta _x^2K_0\eta -\eta _x\eta _z L_0\eta + K_2(\eta )\eta \end{aligned}$$

and the fact that $K_2(\eta )=m_2(\eta ,\eta )$, where $m_2$ is a bounded, symmetric bilinear mapping ${\mathcal Z}\times {\mathcal Z}\rightarrow {\mathcal L}(H^{5/2}(\mathbb {R}^2), H^{3/2}(\mathbb {R}^2))$, that

$$\begin{aligned} {\mathcal L}^\prime _3(\eta _1+F(\eta _1) + \eta _3(\eta _1)) ={\mathcal L}^\prime _3(F(\eta _1)+\eta _1)+\underline{O}(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^4); \end{aligned}$$

using Lemma 2.4(iii) twice yields

$$\begin{aligned} {\mathcal L}^\prime _3(F(\eta _1)+\eta _1) = {\mathcal L}^\prime _3(\eta _1) +\underline{O}(\varepsilon ^{3\theta } |{}|{}|\eta _1 |{}|{}|^3) \end{aligned}$$

and

$$\begin{aligned} \qquad \quad \chi ^+(D){\mathcal L}^\prime _3(\eta _1) = -2\chi ^+(D)\big (\eta _1^-(\eta _1^+)^2\big ) +\underline{O}_+(\varepsilon ^{3\theta } |{}|{}|\eta _1 |{}|{}|^3).\qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad \quad \qquad \quad {\Box } \end{aligned}$$

Proposition 4.7

The estimates

$$\begin{aligned} {\mathcal K}^\prime _\mathrm {r}(\eta _1+F(\eta _1) + \eta _3(\eta _1))&= \underline{O}(\varepsilon ^{4\theta }|{}|{}|\eta _1 |{}|{}|^5), \\ {\mathcal L}^\prime _\mathrm {r}(\eta _1+F(\eta _1) + \eta _3(\eta _1))&= \underline{O}(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^4) \end{aligned}$$

hold for each $\eta _1 \in X_1$.

Proof

This result follows from Proposition 2.5(ii), Corollary 3.4 and Theorem 3.9. $\square$

Proposition 4.8

The estimates

$$\begin{aligned} -\tfrac{1}{2}\chi ^+(D)\big (K_1(\eta _1+F(\eta _1) + \eta _3(\eta _1))(\eta _1+F(\eta _1) + \eta _3(\eta _1))\big )^2&=\underline{O}_+(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^4), \\ -\tfrac{1}{2}\chi ^+(D)\big (L_1(\eta _1+F(\eta _1) + \eta _3(\eta _1))(\eta _1+F(\eta _1) + \eta _3(\eta _1))\big )^2&=\underline{O}_+(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^4) \end{aligned}$$

hold for each $\eta _1 \in X_1$.

Proof

It follows from Corollary 3.4 and Theorem 3.9 that

$$\begin{aligned} -\tfrac{1}{2}\big (K_1(\eta _1+F(\eta _1) + \eta _3(\eta _1))(\eta _1+F(\eta _1) + \eta _3(\eta _1))\big )^2=-\tfrac{1}{2}(K_1(\eta _1)\eta _1)^2 + \underline{O}(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^4), \end{aligned}$$

and furthermore

$$\begin{aligned} -\tfrac{1}{2}\chi ^+(D)(K_1(\eta _1)\eta _1)^2 = -\tfrac{1}{2}\chi ^+(D)\big ((\eta _1\eta _{1x})_x+K_0(\eta _1K_0\eta _1)+L_0(\eta _1 L_0\eta _1)\big )^2=0 \end{aligned}$$

because of equation (2.5). The second estimate is derived in the same fashion (with equation (2.6)). $\square$

Corollary 4.9

The estimate

$$\begin{aligned} \chi ^+(D){\mathcal N}_2(\eta _1,\eta _3(\eta _1))=\tfrac{5}{2}\chi ^+(D)\big (\eta _1^-(\eta _1^+)^2\big )+\underline{O}_+(\varepsilon ^{3\theta }|{}|{}|\eta _1 |{}|{}|^3) \end{aligned}$$

holds for each $\eta _1 \in X_1$.

The reduced equation for $\eta _1$ is therefore

$$\begin{aligned} \eta _1^+-\eta _{1xx}^+-\eta _{1zz}^+-2 K_0\eta _1^+ + 2\varepsilon ^2 K_0 \eta _1^+ - \tfrac{11}{2}\chi ^+(D)\big (|\eta _1^+|^2\eta _1^+\big ) + \underline{O}_+(\varepsilon ^{3\theta } |{}|{}|\eta _1 |{}|{}|^3)=0, \end{aligned}$$

which can be further simplified to

$$\begin{aligned} \eta _1^+-\eta _{1xx}^+-\eta _{1zz}^+-2 K_0\eta _1^+ + 2\varepsilon ^2 \eta _1^+ - \tfrac{11}{2}\chi ^+(D)\big (|\eta _1^+|^2\eta _1^+\big ) + \underline{O}_+(\varepsilon ^{3\theta } |{}|{}|\eta _1 |{}|{}|)=0 \end{aligned}$$

by an application of Lemma 4.2(iv). Finally, we introduce the nonlinear Schrödinger scaling

$$\begin{aligned} \eta _1^+(x,z) = \tfrac{1}{2}\varepsilon \zeta (\varepsilon x,\varepsilon z)\mathrm {e}^{\mathrm {i}x}, \end{aligned}$$

so that $\zeta \in B_R(0) \subseteq \chi _0(\varepsilon D)H^1(\mathbb {R}^2)$ solves the perturbed full-dispersion nonlinear Schrödinger equation

$$\begin{aligned} \varepsilon ^{-2}g(e+\varepsilon D)\zeta + 2\zeta - \tfrac{11}{8}\chi _0(\varepsilon D)(|\zeta |^2\zeta ) + \varepsilon ^{3\theta -2} \underline{O}_0^\varepsilon (\Vert \zeta \Vert _1)=0, \end{aligned}$$

(4.2)

where $R=R_1/\sqrt{2}$ and $e=(1,0)$ (note that $|{}|{}|\eta _1 |{}|{}|^2 = \Vert \zeta \Vert _1^2$ and the change of variables from (x, z) to $\varepsilon (x,z)$ introduces a further factor of $\varepsilon$ in the remainder term). The invariance of the reduced equation under $\eta _1(x,z) \mapsto \eta _1(-x,-z)$ and $\eta _1(x,z) \mapsto \eta _1(x,-z)$ is inherited by (4.2), which is invariant under the reflections $\zeta (x,z) \mapsto \overline{\zeta (-x,z)}$ and $\zeta (x,z) \mapsto \zeta (x,-z)$.

Remark 4.10

In the formal limit $\varepsilon =0$ equation (4.2) reduces to the nonlinear Schrödinger equation

$$\begin{aligned} -\tfrac{1}{2}\zeta _{xx}-\zeta _{zz} + \zeta -\tfrac{11}{16}|\zeta |^2 \zeta =0. \end{aligned}$$

(4.3)

5 Solution of the reduced equation

In this section we complete our existence theory by proving the following theorem.

Theorem 5.1

For each sufficiently small value of $\varepsilon >0$ equation (4.2) has two small-amplitude solutions $\zeta ^\pm _\varepsilon$ in $\chi _0(\varepsilon D)H^1(\mathbb {R}^2)$ which satisfy $\zeta ^\pm _\varepsilon (x,z) = \overline{\zeta ^\pm _\varepsilon (-x,z)}$, $\zeta ^\pm _\varepsilon (x,z) = \zeta ^\pm _\varepsilon (x,-z)$ and $\Vert \zeta ^\pm _\varepsilon - (\pm \zeta _0)\Vert _1 \lesssim \varepsilon ^{1/2}$, where is the unique symmetric, positive (real) solution of the nonlinear Schrödinger equation (4.3).

The first step is a result which allows us to ‘replace’ the nonlocal operator in equation (4.2) by a differential operator.

Proposition 5.2

The inequality

$$\begin{aligned} \left| \frac{\varepsilon ^2}{2\varepsilon ^2 + g(e+\varepsilon k)}- \frac{1}{2+k_1^2+2k_3^2}\right| \lesssim \frac{\varepsilon |k|^3}{(1+|k|^2)^2} \end{aligned}$$

holds uniformly over $|k| < \delta /\varepsilon$.

Proof

Clearly

$$\begin{aligned} \left| \frac{\varepsilon ^2}{2\varepsilon ^2 + g(e+\varepsilon k)}- \frac{1}{2+k_1^2+2k_3^2}\right| = \frac{|g(e+\varepsilon k)-\varepsilon ^2(k_1^2+2k_3^2)|}{(2\varepsilon ^2 + g(e+\varepsilon k))(2+k_1^2+2k_3^2)}, \end{aligned}$$

while

$$\begin{aligned} g(e+s)-s_1^2-2s_2^2 \lesssim |s|^3, \qquad |s| \le \delta , \end{aligned}$$

and

$$\begin{aligned} g(e+s) > rsim |s|^2, \qquad s \in \mathbb {R}^2. \end{aligned}$$

It follows that

$$\begin{aligned} \qquad \qquad \qquad \qquad \left| \frac{\varepsilon ^2}{2\varepsilon ^2 + g(e+\varepsilon k)}- \frac{1}{2+k_1^2+2k_3^2}\right| \lesssim \frac{\varepsilon |k|^3}{(1+|k|^2)^2}, \qquad |k| < \delta /\varepsilon .\qquad \qquad \qquad \qquad \quad {\Box } \end{aligned}$$

Using this proposition, one can write equation (4.2) as

$$\begin{aligned} \zeta +H_\varepsilon (\zeta )=0, \end{aligned}$$

(5.1)

where

$$\begin{aligned} H_\varepsilon (\zeta )=-\tfrac{11}{16}\left( 1-\tfrac{1}{2}\partial _x^2 - \partial _z^2\right) ^{-1}\chi _0(\varepsilon D)\big (|\zeta |^2\zeta \big ) + \varepsilon ^{1/2}\underline{O}_1^\varepsilon (\Vert \zeta \Vert _1) \end{aligned}$$

and we have chosen the concrete value $\theta =5/6$, so that $\varepsilon ^{3\theta -2}=\varepsilon ^{1/2}$. It is convenient to study equation (5.1) in the fixed function space $H^1(\mathbb {R}^2)$ by replacing it by

$$\begin{aligned} \zeta +\tilde{H}_\varepsilon (\zeta )=0, \end{aligned}$$

(5.2)

where $\tilde{H}_\varepsilon (\zeta )=H_\varepsilon (\chi _0(\varepsilon D)\zeta )$ (the solution sets of (5.1) and (5.2) evidently coincide). Equation (5.2) is solved using the following variant of the implicit-function theorem.

Theorem 5.3

Suppose that ${\mathcal X}$ is a Banach space, $X_0$ and $\Lambda _0$ are open neighbourhoods of respectively $x_0$ in ${\mathcal X}$ and the origin in $\mathbb {R}^n$ and ${\mathcal H}: X_0 \times \Lambda _0 \rightarrow {\mathcal X}$ is a mapping which is differentiable with respect to its first argument. Suppose further that ${\mathcal H}(x_0,0)=0$, $\mathrm {d}_1{\mathcal H}[x_0,0]: {\mathcal X}\rightarrow {\mathcal X}$ is an isomorphism,

$$\begin{aligned} \lim _{x \rightarrow x_0}\Vert \mathrm {d}_1{\mathcal H}[x, 0]-\mathrm {d}_1{\mathcal H}[x_0,0]\Vert _{{\mathcal L}({\mathcal X})}=0 \end{aligned}$$

and

$$\begin{aligned} \lim _{\lambda \rightarrow 0} \Vert {\mathcal H}(x,\lambda )-{\mathcal H}(x,0)\Vert _{{\mathcal X}}=0, \quad \lim _{\lambda \rightarrow 0} \ \Vert \mathrm {d}_1{\mathcal H}[x,\lambda ]-\mathrm {d}_1{\mathcal H}[x,0]\Vert _{{\mathcal L}({\mathcal X})}=0 \end{aligned}$$

uniformly over $x \in X_0$.

Under these hypotheses there exist open neighbourhoods X and $\Lambda$ of respectively $x_0$ in ${\mathcal X}$ and $\Lambda$ of the origin in $\mathbb {R}^n$ (with $X \subseteq X_0$, $\Lambda \subseteq \Lambda _0)$ and a uniquely determined mapping $h: \Lambda \rightarrow X$ such that

• (i) $\lim \limits _{\lambda \rightarrow 0} h(\lambda )=h(0)=x_0$,

• (ii) ${\mathcal H}(h(\lambda ),\lambda )=0$ for all $\lambda \in \Lambda$,

• (iii) $x=h(\lambda )$ whenever $(x,\lambda ) \in X \times \Lambda$ satisfies ${\mathcal H}(x,\lambda )=0$.

Furthermore, the estimate $\Vert {\mathcal H}(x,\lambda )-{\mathcal H}(x,0)\Vert _{{\mathcal X}} \lesssim |\lambda |^\alpha$ (with $\alpha >0$) for all $\lambda \in \Lambda _0$ and $x \in X_0$ implies that $\Vert h(\lambda )-h(0)\Vert _{{\mathcal X}} \lesssim |\lambda |^\alpha$ for all $\lambda \in \Lambda$.

We proceed by employing Theorem 5.3 with

$$\begin{aligned} {\mathcal X}=H_\mathrm {e}^1(\mathbb {R}^2,\mathbb {C})=\{\zeta \in H^1(\mathbb {R}^2,\mathbb {C}): \zeta (x,z) = \overline{\zeta (-x,z)}, \ \zeta (x,z) = \zeta (x,-z)\} \end{aligned}$$

and $X=B_R(0)$, $\Lambda _0=(-\varepsilon _0,\varepsilon _0)$, where R and $\varepsilon _0$ are chosen respectively sufficiently large (to accommodate the requirement that $\zeta _0 \in X$) and sufficiently small. Note that negative values of $\varepsilon$ have been included so that we can define

$$\begin{aligned} {\mathcal H}(\zeta ,\varepsilon ):=\zeta +\tilde{H}_{|\varepsilon |}(\zeta ) \end{aligned}$$

for $\varepsilon$ in the full neighbourhood $\Lambda _0$ of the origin in $\mathbb {R}$. We also henceforth explicitly indicate whether functions are real- or complex-valued.

Observe that

$$\begin{aligned} {\mathcal H}(\zeta&,\varepsilon )-{\mathcal H}(\zeta ,0) \\&= -\tfrac{11}{16}\left( 1-\tfrac{1}{2}\partial _x^2 - \partial _z^2\right) ^{-1}\bigg (\chi _0(|\varepsilon | D)\Big (|\chi _0({|\varepsilon |} D)\zeta |^2\chi _0({|\varepsilon |} D)\zeta \Big )-|\zeta |^2\zeta \bigg ) + {|\varepsilon |}^{1/2}\underline{O}_1^{|\varepsilon |}(\Vert \zeta \Vert _1) \\&= -\tfrac{11}{16}\left( 1-\tfrac{1}{2}\partial _x^2 - \partial _z^2\right) ^{-1}\bigg (\chi _0(|\varepsilon | D)\Big ( |\chi _0({|\varepsilon |}D)\zeta |^2\big (\chi _0({|\varepsilon |} D)-I\big )\zeta +|\zeta |^2\big (\chi _0({|\varepsilon |} D)-I\big )\zeta \\&\quad \quad \quad \quad \quad \quad \qquad \qquad \qquad \qquad \quad + \zeta \chi _0({|\varepsilon |}D)\zeta \big (\chi _0({|\varepsilon |} D)-I\big )\overline{\zeta } \Big )\\&\quad \quad \quad \quad \quad \qquad \qquad \qquad \quad +\Big (\chi _0({|\varepsilon |} D)-I\Big )|\zeta |^2\zeta \bigg ) + {|\varepsilon |}^{1/2}\underline{O}_1^{|\varepsilon |}(\Vert \zeta \Vert _1). \end{aligned}$$

Noting that

$$\begin{aligned} \Vert \chi _0(|\varepsilon | D) - I\Vert _{{\mathcal L}(H^1({\mathbb {R}}^2,\mathbb {C}), H^{1/2}({\mathbb {R}}^2,\mathbb {C}))} \lesssim |\varepsilon |^{1/2} \end{aligned}$$

because

$$\begin{aligned} \Vert \chi _0(|\varepsilon | D) u - u \Vert _{1/2}^2&= \int _{|k|> \frac{\delta }{|\varepsilon |}} (1+|k|^2)^{1/2} |\hat{u}|^2 \, \mathrm {d}k\\&\le \sup _{|k|> \frac{\delta }{|\varepsilon |}} (1+|k|^2)^{-1/2} \int _{|k| > \frac{\delta }{|\varepsilon |}} (1+|k|^2) |\hat{u}|^2 \, \mathrm {d}k\\&\le \frac{1}{\big (1+\frac{\delta ^2}{|\varepsilon |^2}\big )^{1/2}} \Vert u\Vert _1^2, \end{aligned}$$

and similarly

$$\begin{aligned} \Vert \chi _0(|\varepsilon | D) - I\Vert _{{\mathcal L}(H^{1/2}({\mathbb {R}}^2,\mathbb {C}), L^2({\mathbb {R}}^2,\mathbb {C}))} \lesssim |\varepsilon |^{1/2}, \end{aligned}$$

and that pointwise multiplication defines bounded trilinear mappings $H^1(\mathbb {R}^2,\mathbb {C})^3 \rightarrow H^{1/2}(\mathbb {R}^2,\mathbb {C})$ and $H^1(\mathbb {R}^2,\mathbb {C})^2 \times H^{1/2}(\mathbb {R}^2,\mathbb {C}) \rightarrow L^2(\mathbb {R}^2,\mathbb {C})$ (see Hörmander [10, Theorem 8.3.1]), we find that

$$\begin{aligned} \Vert {\mathcal H}(\zeta ,\varepsilon )-{\mathcal H}(\zeta ,0)\Vert _1 \lesssim |\varepsilon |^{1/2} \end{aligned}$$

uniformly over $\zeta \in B_R(0)$. Here we have also used the estimate $\Vert \chi _0(|\varepsilon | D)u \Vert _s \le \Vert u\Vert _s$ for all $u \in H^s(\mathbb {R}^2,\mathbb {C})$ and and the fact that $\left( 1-\tfrac{1}{2}\partial _x^2 - \partial _z^2\right) ^{-1}$ maps $L^2({\mathbb {R}}^2,\mathbb {C})$ continuously into $H^1({\mathbb {R}}^2,\mathbb {C})$. A similar calculation shows that

$$\begin{aligned} \Vert \mathrm {d}_1{\mathcal H}[\zeta ,\varepsilon ]-\mathrm {d}_1{\mathcal H}[\zeta ,0]\Vert _{{\mathcal L}(H^1(\mathbb {R}^2,\mathbb {C}))} \lesssim |\varepsilon |^{1/2} \end{aligned}$$

uniformly over $\zeta \in B_R(0)$.

Furthermore, the equation

$$\begin{aligned} {\mathcal H}(\zeta ,0)=\zeta -\tfrac{11}{16}\left( 1-\tfrac{1}{2}\partial _x^2 - \partial _z^2\right) ^{-1}|\zeta |^2\zeta =0 \end{aligned}$$

(5.3)

has a unique symmetric, positive (real) solution (see Sulem and Sulem [21, §4.2] and the references therein). We show that $\mathrm {d}_1{\mathcal H}[\pm \zeta _0,0]$ is an isomorphism by means of real coordinates $\zeta _1={{\,\mathrm{Re}\,}}\zeta$ and $\zeta _2={{\,\mathrm{Im}\,}}\zeta$, in terms of which

$$\begin{aligned} \mathrm {d}_1{\mathcal H}[\pm \zeta _0,0](\zeta _1+\mathrm {i}\zeta _2)={\mathcal H}_1(\zeta _1) + \mathrm {i} {\mathcal H}_2(\zeta _2), \end{aligned}$$

where ${\mathcal H}_1: H_\mathrm {e}^1(\mathbb {R}^2,\mathbb {R}) \rightarrow H_\mathrm {e}^1(\mathbb {R}^2,\mathbb {R})$ and ${\mathcal H}_2: H_\mathrm {o}^1(\mathbb {R}^2,\mathbb {R}) \rightarrow H_\mathrm {o}^1(\mathbb {R}^2,\mathbb {R})$ are defined by

$$\begin{aligned} {\mathcal H}_1(\zeta _1)=\zeta _1 - \tfrac{33}{16}\left( 1-\tfrac{1}{2}\partial _x^2 - \partial _z^2\right) ^{-1} \zeta _0^2 \zeta _1, \qquad {\mathcal H}_2(\zeta _2)=\zeta _2 - \tfrac{11}{16}\left( 1-\tfrac{1}{2}\partial _x^2 - \partial _z^2\right) ^{-1} \zeta _0^2 \zeta _2 \end{aligned}$$

with

$$\begin{aligned} H^n_\mathrm {e}(\mathbb {R}^2,\mathbb {R})&= \{\zeta _1 \in H^n(\mathbb {R}^2,\mathbb {R}): \zeta _1(x,z)=\zeta _1(-x,z),\ \zeta _1(x,z)=\zeta _1(x,-z)\}, \\ H^n_\mathrm {o}(\mathbb {R}^2,\mathbb {R})&= \{\zeta _2 \in H^n(\mathbb {R}^2,\mathbb {R}): \zeta _2(x,z)=-\zeta _2(-x,z),\ \zeta _2(x,z)=\zeta _1(x,-z)\} \end{aligned}$$

for $n \in {\mathbb {N}}_0$. The formulae

$$\begin{aligned} \zeta _1 \mapsto \tfrac{33}{16}\left( 1-\tfrac{1}{2}\partial _x^2 - \partial _z^2\right) ^{-1} \zeta _0^2 \zeta _1, \qquad \zeta _2 \mapsto \tfrac{11}{16}\left( 1-\tfrac{1}{2}\partial _x^2 - \partial _z^2\right) ^{-1} \zeta _0^2 \zeta _2 \end{aligned}$$

define compact operators $H^1(\mathbb {R}^2,\mathbb {R}) \rightarrow H^1(\mathbb {R}^2,\mathbb {R})$, $H^1_\mathrm {e}(\mathbb {R}^2,\mathbb {R}) \rightarrow H^1_\mathrm {e}(\mathbb {R}^2,\mathbb {R})$ and $H^1_\mathrm {o}(\mathbb {R}^2,\mathbb {R}) \rightarrow H^1_\mathrm {o}(\mathbb {R}^2,\mathbb {R})$, so that $H_1$, $H_2$ are Fredholm with index 0. Writing

$$\begin{aligned} T_1\zeta _1 = \zeta _1 - \tfrac{1}{2}\zeta _{1xx}-\zeta _{1zz} - \tfrac{33}{16}\zeta _0^2\zeta _1, \qquad T_2\zeta _2 = \zeta _2 - \tfrac{1}{2}\zeta _{2xx}-\zeta _{2zz} - \tfrac{11}{16}\zeta _0^2 \zeta _2, \end{aligned}$$

we find that the kernels of ${\mathcal H}_1$ and ${\mathcal H}_2$ coincide with respectively the kernels of the linear operators $T_1: H^2_\mathrm {e}(\mathbb {R}^2,\mathbb {R}) \subseteq L^2_\mathrm {e}(\mathbb {R}^2,\mathbb {R}) \rightarrow L^2_\mathrm {e}(\mathbb {R}^2,\mathbb {R})$ and $T_2: H^2_\mathrm {o}(\mathbb {R}^2,\mathbb {R}) \subseteq L^2_\mathrm {o}(\mathbb {R}^2,\mathbb {R}) \rightarrow L^2_\mathrm {o}(\mathbb {R}^2,\mathbb {R})$. It is however known that the kernels of $T_1$, $T_2: H^2(\mathbb {R}^2,\mathbb {R}) \subseteq L^2(\mathbb {R}^2,\mathbb {R}) \rightarrow L^2(\mathbb {R}^2,\mathbb {R})$ are respectively $\langle \zeta _{0x}, \zeta _{0z}\rangle$ and $\langle \zeta _0\rangle$ (see Chang et al. [5]). The kernels of ${\mathcal H}_1$, ${\mathcal H}_2$ are therefore trivial, so that ${\mathcal H}_1$, ${\mathcal H}_2$ and hence $\mathrm {d}_1{\mathcal H}[\pm \zeta _0,0]$ are isomorphisms.

It remains to confirm that the formulae

$$\begin{aligned} \eta = \eta _1 + F(\eta _1) + \eta _3(\eta _1), \quad \eta _1=\eta _1^++\overline{\eta _1^+}, \quad \eta _1^+(x,z) = \tfrac{1}{2}\zeta ^\pm _\varepsilon (\varepsilon x, \varepsilon z)\mathrm {e}^{\mathrm {i}x} \end{aligned}$$

lead to the estimate

$$\begin{aligned} \eta (x,z)=\pm \varepsilon \zeta _0(\varepsilon x,\varepsilon z)\cos x + o(\varepsilon ) \end{aligned}$$

uniformly over $(x,z) \in \mathbb {R}^2$. The key is to show that

$$\begin{aligned} \Vert \zeta ^+_\varepsilon -\zeta _0\Vert _\infty \lesssim \varepsilon ^\Delta \end{aligned}$$

for any $\Delta \in (0,1/2)$; here we choose the concrete value $\Delta =1/4$. This result follows from the calculation

$$\begin{aligned} \Vert \zeta _\varepsilon ^+-\zeta _0\Vert _\infty&\lesssim \Vert \zeta _\varepsilon ^+-\zeta _0\Vert _{5/4} \\&= \Vert (1+|k|^2)^{5/8}(\hat{\zeta }_\varepsilon ^+-\hat{\zeta }_0)\Vert _{L^2(|k|<\delta /\varepsilon )}+ \Vert (1+|k|^2)^{5/8}\hat{\zeta }_0\Vert _{L^2(|k|>\delta /\varepsilon )} \end{aligned}$$

(because the support of $\hat{\zeta }_\varepsilon$ lies in $\overline{B}_{\delta /\varepsilon }(0)$) and

$$\begin{aligned} \Vert (1+|k|^2)^{5/8}(\hat{\zeta }_\varepsilon ^+-\hat{\zeta }_0)\Vert _{L^2(|k|<\delta /\varepsilon )}&\lesssim \varepsilon ^{-1/4}\Vert (1+|k|^2)^{1/2}(\hat{\zeta }_\varepsilon ^+-\hat{\zeta }_0)\Vert _{L^2(|k|<\delta /\varepsilon )} \\&\le \varepsilon ^{-1/4}\Vert (1+|k|^2)^{1/2}(\hat{\zeta }_\varepsilon ^+-\hat{\zeta }_0)\Vert _0 \\&= \varepsilon ^{-1/4}\Vert \zeta _\varepsilon ^+-\zeta _0\Vert _1, \\&\lesssim \varepsilon ^{1/4}, \\ \\ \Vert (1+|k|^2)^{5/8}\hat{\zeta }_0^+\Vert _{L^2(|k|>\delta /\varepsilon )}^2&= \int _{|k|>\frac{\delta }{\epsilon }} (1+|k|^2)^{5/4} |\hat{\zeta }_0|^2 \\&\lesssim \varepsilon \end{aligned}$$

(because , so that in particular $|\hat{\zeta }_0(|k|)|^2 \lesssim (1+|k|^2)^{-11/4}$). It follows that

$$\begin{aligned} \eta _1^+(x,z)&= \varepsilon \zeta _0(\varepsilon x,\varepsilon z)\mathrm {e}^{\mathrm {i}x} +\tfrac{1}{2}\varepsilon (\zeta _\varepsilon ^+-\zeta _0)(\varepsilon x,\varepsilon z)\mathrm {e}^{\mathrm {i}x} \\&= \varepsilon \zeta _0(\varepsilon x,\varepsilon z)\mathrm {e}^{\mathrm {i}x} + O(\varepsilon ^{5/4}), \end{aligned}$$

uniformly in (x, z). (These estimates remain valid when $\zeta _\varepsilon ^+$ and $\zeta _0$ are replaced by respectively $\zeta _\varepsilon ^-$ and $-\zeta _0$.)

Furthermore

$$\begin{aligned} \Vert \eta _3(\eta _1)\Vert _\infty \lesssim \Vert \eta _3(\eta _1)\Vert _3 \lesssim \varepsilon ^{10/6} |{}|{}|\eta _1 |{}|{}|^2 \lesssim \varepsilon ^{10/6} \end{aligned}$$

by Theorem 3.9 (recall that we have chosen $\theta =5/6)$, while

$$\begin{aligned} \Vert F(\eta _1)\Vert _\infty =O(\varepsilon ^{11/6}) \end{aligned}$$

because

$$\begin{aligned} F(\eta _1) = -2\left( (\eta _1^+)^2+\big (\overline{\eta _1^+}\big )^2\right) +F_\mathrm {r}(\eta _1), \end{aligned}$$

where

$$\begin{aligned} \Vert F_\mathrm {r}(\eta _1)\Vert _\infty \lesssim \Vert F_\mathrm {r}(\eta _1)\Vert _3 \lesssim \Vert F_\mathrm {r}(\eta _1)\Vert _1 \lesssim \varepsilon ^{11/6}|{}|{}|\eta _1|{}|{}|^2 \lesssim \varepsilon ^{11/6} \end{aligned}$$

(see Proposition 4.3; the second estimate follows by the fact that the support of ${\mathcal F}[F_\mathrm {r}(\eta _1)]$ is bounded independently of $\varepsilon$).