Skip to main content
SpringerLink
Log in

Existence Theory for Stochastic Power Law Fluids

  • Published:
Journal of Mathematical Fluid Mechanics Aims and scope Submit manuscript

Abstract

We consider the equations of motion for an incompressible non-Newtonian fluid in a bounded Lipschitz domain \({G {\subset} \mathbb{R}^{d}}\) during the time interval (0, T) together with a stochastic perturbation driven by a Brownian motion W. The balance of momentum reads as

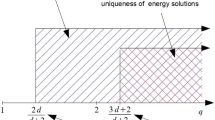
$${\rm {d}\mathbf{v}} = {\rm div}\mathbf{S} {\rm d}t-(\nabla \mathbf{v})\mathbf{v} {\rm d}t + \nabla\pi {\rm d}t + \mathbf{f}{\rm d}t + \Phi(\mathbf{v}) {\rm d}\mathbf{W}_{t},$$

where v is the velocity, \({\pi}\) the pressure and f an external volume force. We assume the common power law model \({\mathbf{S}(\varepsilon(\mathbf{v}))=(1+|\varepsilon(\mathbf{v})|)^{p-2}\varepsilon(\mathbf{v})}\) and show the existence of martingale weak solution provided \({p > \frac{2d+2}{d+2}}\). Our approach is based on the \({L^{\infty}}\)-truncation and a harmonic pressure decomposition which are adapted to the stochastic setting.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Amann H.: Compact embeddings of vector-valued Sobolev and Besov spaces. Glass. Mat. III. Ser. 35(55), 161–177 (2000)

    MATH  MathSciNet  Google Scholar 

  2. Astarita G., Marrucci G.: Principles of Non-Newtonian Fluid Mechanics. McGraw-Hill, London (1974)

    Google Scholar 

  3. Arnold L.: Stochastic Differential Equations: Theory and Applications. Wiley, New York (1973)

    Google Scholar 

  4. Bird R., Armstrong R., Hassager O.: Dynamics of Polymeric Liquids, vol. 1. Fluid Mechanics, 2nd edn. Wiley, New York (1987)

    Google Scholar 

  5. Bensoussan A., Temam R.: Équations stochastiques du type Navier–Stokes (French). J. Funct. Anal. 13, 195–222 (1973)

    Article  MATH  MathSciNet  Google Scholar 

  6. Bogovskiĭ, M.E.: Solutions of some problems of vector analysis, associated with the operators div and grad. In: Theory of cubature formulas and the application of functional Analysis to Problems of Mathematical Physics (Russian), vol. 149. Akad. Nauk SSSR Sibirsk. Otdel. Inst. Mat., Novosibirsk, pp. 5–40 (1980)

  7. Breit D., Diening L., Schwarzacher S.: Solenoidal Lipschitz truncation for parabolic PDE’s. Math. Model Methods Appl. Sci. 23, 2671–2700 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  8. Breit, D., Hofmanová, M.: Stochastic Navier–Stokes equations for compressible fluids. Preprint at arXiv:1409.2706v1

  9. Chen J., Chen Z.-M.: Stochastic non-Newtonian fluid motion equations of a nonlinear bipolar viscous fluid. J. Math. Anal. Appl. 369(2), 486–509 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  10. Clément Ph., Sweers G.: Uniform anti-maximum principles for polyharmonic equations. Proc. Am. Math. Soc. 129, 467–474 (2000)

    Article  Google Scholar 

  11. Clément Ph., Sweers G.: Uniform anti-maximum principles. J. Differ. Equ. 164, 118–154 (2000)

    Article  ADS  MATH  Google Scholar 

  12. Da Prato, G., Zabczyk, J.: Stochastic Equations in Infinite Dimensions. Encyclopedia Math. Appl., vol. 44. Cambridge University Press, Cambridge (1992)

  13. Debussche, A., Glatt-Holtz, N., Temam, R.: Local Martingale and pathwise solutions for an abstract fluids model. Phys. D Nonlinear Phenom. 240(14–15), 1123–1144 (2011)

  14. Debussche, A., Hofmanova, M., Vovelle, J.: Degenerate parabolic stochastic partial differential equations: quasilinear case. Preprint at arXiv:1309.5817v1 (to appear in Ann. Prob.)

  15. Diening L., Málek J., Steinhauer M.: On Lipschitz truncations of Sobolev functions (with variable exponent) and their selected applications. ESAIM Control Optim. Calc. Var. 14(2), 211–232 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  16. Diening L., Růžička M., Wolf J.: Existence of weak solutions for unsteady motions of generalized Newtonian fluids. Ann. Sc. Norm. Sup. Pisa Cl. Sci. (5) IX(2010), 1–46 (2010)

    Google Scholar 

  17. Flandoli, F.: An introduction to 3D stochastic fluid dynamics. In SPDE in Hydrodynamic: Recent Progress and Prospects. Lecture Notes in Math., vol. 1942. Springer, Berlin, pp. 51–150 (2008)

  18. Friedman A.: Stochastic Differential Equations and Applications I. Academic Press, New York (1975)

    Google Scholar 

  19. Friedman A.: Stochastic Differential Equations and Applications II. Academic Press, New York (1976)

    Google Scholar 

  20. Frehse J., Málek J., Steinhauer M.: An existence result for fluids with shear dependent viscosit–steady flows. Nonlinear Anal. 30, 3041–3049 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  21. Frehse, J., Málek, J., Steinhauer, M.: On analysis of steady flows of fluids with shear-dependent viscosity based on the Lipschitz truncation method. SIAM J. Math. Anal. 34(5), 1064-1083 (2003) (electronic)

  22. Galdi, G.: An Introduction to the Mathematical Theory of the Navier–Stokes Equations, vol. I. Springer Tracts in Natural Philosophy, vol. 38. Springer, Berlin (1994)

  23. Galdi, G.: An Introduction to the Mathematical Theory of the Navier–Stokes Equations, vol. II. Springer Tracts in Natural Philosophy, vol. 39. Springer, Berlin (1994)

  24. Hoffmanová, M.: Degenerate parabolic stochastic partial differential equations. Stoch. Pr. Ap. 123(12), 4294–4336

  25. Ikeda, N., Watanabe, S.: Stochastic Differential Equations and Diffusion Processes, 2nd edn. North-Holland Mathematical Library 24. North-Holland, Amsterdam (1989)

  26. Jakubowski, A.: The almost sure Skorokhod representation for subsequences in nonmetric spaces. Teor. Veroyatnost. i Primenen 42, no. 1, 209–216 [translation in Theory Probab. Appl. 42, no. 1, 167–174 (1997/1998)]

  27. Ladyzhenskaya O.A.: The Mathematical Theory of Viscous Incompressible Flow. Gordon and Breach, UK (1969)

    MATH  Google Scholar 

  28. Ladyzhenskaya O.A.: On some new equations describing dynamics of incompressible fluids and on global solvability of boundary value problems to these equations. Trudy Steklov’s Math. Inst. 102, 85–104 (1967)

    MATH  Google Scholar 

  29. Ladyzhenskaya O.A.: On some modifications of the Navier–Stokes equations for large gradients of velocity. Zap. Nauchn. Sem. Leningrad. Otdel. Mat. Inst. Steklov (LOMI) 7, 154–154 (1968)

    MATH  MathSciNet  Google Scholar 

  30. Lions, J.L.: Quelques méthodes de résolution des problèmes aux limites non linéaires (1969)

  31. Mikulevicius R., Rozovskii B.L.: Stochastic Navier–Stokes equations for turbulent flows. SIAM J. Math. Anal. 35(5) 1310–1310 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  32. Müller, R.: Das schwache Dirichletproblem in L q für den Bipotentialoperator in beschränkten Gebieten und in Auβengebieten. Bayreuth. Math. Schr. (1995), no. 49, 115–211, Dissertation, Universität Bayreuth, Bayreuth (1994)

  33. Málek J., Nečas J., Rokyta M., Růžička M.: Weak and Measure Valued Solutions to Evolutionary PDEs. Chapman & Hall, London (1996)

    Book  MATH  Google Scholar 

  34. Ondreját M.: Stochastic nonlinear wave equations in local Sobolev spaces. Electron. J. Probab. 15(33), 1041–1091 (2010)

    MATH  MathSciNet  Google Scholar 

  35. Prévôt, C., Röckner, M.: A Concise Course on Stochastic Partial Differential Equations. Lecture Notes in Mathematics, vol. 1905. Springer, Berlin (2007)

  36. Terasawa Y., Yoshida N.: Stochastic power-law fluids: existence and uniqueness of weak solutions. Ann. Appl. Probab. 21(5), 1827–1859 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  37. Wolf J.: Existence of weak solutions to the equations of nonstationary motion of non- Newtonian fluids with shear-dependent viscosity. J. Math. Fluid Mech. 9, 104–138 (2007)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  38. Yoshida N.: Stochastic Shear thickenning fluids: strong convergence of the Galerkin approximation and the energy inequality. Ann. Appl. Probab. 22(3), 1215–1242 (2012)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Heriot-Watt University, Edinburgh, EH14 4AS, UK

    Dominic Breit

  2. Mathematical Institute, LMU Munich, Theresienstraβe 39, 80333, Munich, Germany

    Dominic Breit

Authors
  1. Dominic Breit
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dominic Breit.

Additional information

Communicated by H. Beirão da Veiga

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Breit, D. Existence Theory for Stochastic Power Law Fluids. J. Math. Fluid Mech. 17, 295–326 (2015). https://doi.org/10.1007/s00021-015-0203-z

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00021-015-0203-z

Mathematics Subject Classification

Keywords

Search

Navigation