General Position Sets in Two Families of Cartesian Product Graphs

Abstract

For a given graph G, the general position problem asks for the largest set of vertices $S \subseteq V(G)$, such that no three distinct vertices of S belong to a common shortest path of G. The general position problem for Cartesian products of two cycles as well as for hypercubes is considered. The problem is completely solved for the first family of graphs, while for the hypercubes, some partial results based on reduction to SAT are given.

1 Introduction and Preliminaries

Given an ${\displaystyle n\times n}$ grid of points, the no-three-in-line problem asks to select as many as possible points, so that no three points lie on the same line [2]. In computational geometry, finite sets of points with no-three-in-line are said to be in general position. The problem can be generalized to an arbitrary metric space to find its largest subset of points that is in general position, e.g., [10].

It is well known that the standard distance between two vertices of a graph (defined as the length of a shortest path between them) is a metric. In this context, the general position problem was extended to the graph theory as follows. For a given graph G, the goal of the problem is to find a largest set of vertices $S \subseteq V(G)$, such that no three distinct vertices of S belong to a common shortest path of G [1, 8].

Shortly after the seminal papers, the problem has been investigated in interconnection networks with the emphasis on grid graphs [9]. These results motivated studies of the general position problem in various other related families of graphs which can be described as Cartesian product graphs [13, 14]. For an extended list of references, see [4], where, among others families of graphs, the general position problem in Cartesian products of two cycles is considered. In particular, it is shown that for two cycles $C_s$ and $C_t$ with at least six vertices, one can always find a general position set of cardinality 6 in $C_s \Box C_t$. On the other hand, it is established that $C_s \Box C_t$ does not admit a general position set of cardinality 8.

The general position problem for two families of graphs: Cartesian products of two cycles and hypercubes is considered in this paper. In the sequel of this section, we present definitions and results needed in the rest of the paper. In the following section, we solve the general position set problem in $C_s \Box C_t$ for s and t up to 6. Section 3 shows that the largest general position set in $C_s \Box C_t$ is of cardinality 7 if s and t are at least 7. In Sect. 4, we describe a reduction from the problem of finding a general position set in a graph to the satisfiability problem. The results of the approach applied in hypercubes are shown.

If $G = (V(G), E(G))$ is a graph, then $S \subseteq V (G)$ is a general position set if, for every triple of vertices $u,v,w \in V(G)$, we have $d_G(u, v) \not = d_G(u,w) + d_G(w,v)$, where $d_G(u,v)$ (or simply d(u, v)) denotes the length of a shortest u, v-path (a path between u and v) in G. The cardinality of a largest general position set of in G is called the general position number of G and denoted as gp(G).

The Cartesian product of graphs G and H is the graph $G \Box H$ with vertex set $V(G) \times V(H)$ and $(x_1,x_2)(y_1,y_2) \in E(G \Box H)$ whenever $x_1y_1 \in E(G)$ and $x_2=y_2$, or $x_2y_2 \in E(H)$ and $x_1=y_1$. It is well known that the Cartesian product is commutative and associative, having the trivial graph as a unit.

The vertex set of the h-dimensional hypercube, denoted by $Q_h$, consists of all binary strings $u=u_1 u_2 \ldots u_h$, $u_i \in \{0,1\}$. Two vertices x, y are adjacent in $Q_h$ if and only if x and y differ in precisely one place. Note that $K_2^{\Box ,h}$ is isomorphic to the h-dimensional hypercube $Q_h$.

The interval I(u, v) between two vertices u and v of a graph G is the set of vertices on shortest u, v-paths.

The following result is shown in [4].

Theorem 1.1

If $s \ge t \ge 4$, $t \not = 4$, and $s \ge 6$, then $6 \le gp(C_s \Box C_t) \le 7$. Moreover, if $s \ge t \ge 3$, then $gp(C_s \Box C_t) \le 7$.

For positive integers n and k, $n \not = k$, we will use the notation $[k] = \{1, 2, \ldots , k\}$, $[k]_0 = \{0, 1, \ldots , k-1\}$ and

$$\begin{aligned}{}[k,n] = \left\{ \begin{array}{llll} \{k, k+1, \ldots , n\}, &{} n \ge k \\ \{n, n+1, \ldots , k\}, &{} k > n \\ \end{array}. \right. \end{aligned}$$

For a positive integer s and $n,k \in [s_0]$, such that $n,k < s$ and $n \not = k$ let

$$\begin{aligned} |n - k|_s = \min \{ |n - k|, s - |n - k|\}. \end{aligned}$$

Moreover, let

$$\begin{aligned}{}[k,n]_s = \left\{ \begin{array}{llll} [k,n], &{} |n - k|_s < \frac{s}{2} \\ {[s]_0}, &{} |n - k|_s = \frac{s}{2} \\ {[s]_0} \setminus [k,n], &{} \, |n - k|_s > \frac{s}{2} \\ \end{array}. \right. \end{aligned}$$

We will assume that $V(C_s)=[s]_0$ for every $s\ge 4$. Thus, if $u \in V(C_s \Box C_t)$, we write $u=(u_x,u_y)$, where $u_x \in [s]_0$ and $u_y \in [t]_0$. If $i \in [t]_0$, then the subgraph of $C_s \Box C_t$ induced by $V (C_s) \times \{i\}$ is isomorphic to $C_s$ and denoted $C_s^i$.

The following result can be easily confirmed.

Claim 1.2

Let $u,v,z \in V(C_s \Box C_t)$. Then, $z \in I(u,v)$ if and only if $z_x \in [u_x,v_x]_s$ and $z_y \in [u_y,v_y]_t$.

2 Cartesian Products with One Short Cycle

Lemma 2.1

If $s \ge 4$, then $gp(C_s \Box C_4) \ge 5$.

Proof

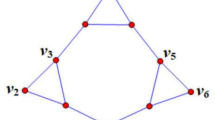
General position sets of cardinality 5 for $C_4 \Box C_4$ and $C_5 \Box C_4$ are shown in Fig. 1.

Let $S'=\{ (0,0), (1,2), (2,3), (3,1) \}$ and $S= S' \cup \{ (\lfloor {s \over 2} \rfloor +1, 2) \}$. One can easily confirm that S is a general position set for $s = 6,7$. We will show that this assertion also holds for $s\ge 8$.

Let $s\ge 8$. Note first that $d((1,2),(2,3)) = 2$, while for every other pair of vertices $\{ u, v \} \subset S'$ and $\{ u, v \} \not = \{ (1,2), (2,3) \}$, we have $d(u,v) \in \{ 3, 4 \}$. Thus, any triple of vertices from $S'$ cannot belong to a common shortest path. Moreover, we have $d((0,0),(\lfloor {s \over 2} \rfloor +1, 2)) = \lfloor {s \over 2} \rfloor +1$, $d((1,2),(\lfloor {s \over 2} \rfloor +1, 2)) = \lfloor {s \over 2} \rfloor$, $d((2,3),(\lfloor {s \over 2} \rfloor +1, 2)) = \lfloor {s + 1 \over 2} \rfloor$ and $d((3,1),(\lfloor {s \over 2} \rfloor +1, 2)) = \lfloor {s -1 \over 2} \rfloor$.

Note that $d(u, (\lfloor {s \over 2} \rfloor +1, 2)) \ge 3$ for $s \ge 8$ and $u \in S'$. Furthermore, we have $d((0,0),(3,1)) = 4$, $d((0,0),(\lfloor {s \over 2} \rceil +1, 2)) \ge 5$ and $d((3,1),(\lfloor {s \over 2} \rceil +1, 2)) \ge 3$. Since $d((0,0),(\lfloor {s \over 2} \rceil +1, 2)) - d((3,1),(\lfloor {s \over 2} \rfloor +1, 2)) \le 2$, the vertices (0, 0), (3, 1) and $(\lfloor {s \over 2} \rfloor +1, 2))$ cannot belong to a common shortest path. In addition, since, for every other pair of vertices $u, v \in S'$ where $\{ u, v \} \not = \{ (0,0), (3,1) \}$, we have $d(u,(\lfloor {s \over 2} \rfloor +1, 2)) - d(v,(\lfloor {s \over 2} \rfloor +1, 2)) \le 1$, the vertices u, v and $(\lfloor {s \over 2} \rfloor +1, 2))$ cannot belong to a common shortest path.

This assertion concludes the proof. $\square$

Fig. 1

General position sets of cardinality 5 in $C_{4} \Box C_{4}$ (left) and $C_{5} \Box C_{4}$ (right)

Proposition 2.2

Let S be a general position set of $C_s \Box C_t$, $s \ge t \ge 4$. If $|S \cap C_s^i|=3$ for $i \in [t]_0$, then $|S|=3$.

Proof

Let S be a general position set of $C_s \Box C_t$, such that $|S \cap C_s^i|=3$. Suppose to the contrary that $|S|>3$. Let $S \cap C_s^i = \{a, b, c \}$ and $d \in S {\setminus } C_s^i$. We may assume w.l.o.g. that $i=0$, $a_x< b_x < c_x$, $d_x = \lfloor {s \over 2} \rfloor$ and $0 < d_y \le {t \over 2}$. Since $b_x \in [a_x,d_x]_s$ or $b_x \in [c_x,d_x]_s$, we can conclude that b belongs to a shortest a, d-path or a shortest c, d-path. $\square$

Proposition 2.3

Let $i \not = j$ and $s \ge t \ge 4$. If S is a general position set of $C_s \Box C_t$, such that $S \cap C_s^i= \{u, w \}$ and $S \cap C_s^j= \{ v \}$, then $v_x \not = u_x$ and $v_x \not = w_x$.

Proof

If $S \cap C_s^i= \{u, w \}$, $S \cap C_s^i= \{ v \}$, and $v_x = u_x$ (resp. $v_x = w_x$), then u (resp. w) is on a shortest v, w-path (resp. v, u-path). $\square$

Proposition 2.4

Let S be a general position set of $C_s \Box C_t$, $s \ge t \ge 4$. If $|S \cap C_s^i|=|S \cap C_s^j|=2$ and $i\not = j$, then we can find a notation, such that $u_x< v_x< w_x < z_x$, where $S \cap C_s^i= \{u, w \}$ and $S \cap C_s^j= \{v, z \}$. Moreover, $v_x - u_x <{s \over 2}$, $w_x - v_x < {s \over 2}$, $z_x - w_x < {s \over 2}$ and $s + u_x - z_x < {s \over 2}$.

Proof

Let $S \cap C_s^i= \{u, w \}$ and $S \cap C_s^j= \{v, z \}$. Suppose w.l.o.g. that $0<j-i \le {t \over 2}$. Note that, by Proposition 2.3, the first coordinate of a vertex of $\{u, w \}$ cannot coincide with the first coordinate of a vertex of $\{v, z \}$. Since $C_s \Box C_t$ is vertex transitive, we can find a notation, such that $u_x = \min \{u_x, v_x, w_x, z_x \}$ and $v_x < z_x$. If $w_x < v_x$ and $u_x - v_x \le {s \over 2}$, then w belongs to a shortest u, v-path and we obtain a contradiction. If $w_x < v_x$ and $u_x - v_x > {s \over 2}$, then $z_x \in [v_x - u_x ]_s$. It follows that z belongs to a shortest v, u-path and we again obtain a contradiction. Since we analogously obtain a contradiction for the case $w_x > z_x$, it follows that $u_x< v_x< w_x < z_x$.

To see that $v_x - u_x < {s \over 2}$, assume to the contrary that $v_x - u_x \ge {s \over 2}$. We can see that $z_x \in [u_x - v_x ]_s$, which in turn means that z belongs to a shortest u, v-path and we obtain a contradiction. Since the proof for the other cases is analogous, the proof is complete. $\square$

Proposition 2.5

Let $i\not = j$ and $s \ge t \ge 4$. If S is a general position set in $C_s \Box C_t$, such that $|S \cap C_s^i|=|S \cap C_s^j|=2$, then $|S \cap C_s^k|=0$ for every $k \in [i,j]_t \setminus \{i,j\}$.

Proof

Let $S \cap C_s^i = \{u, w \}$ and $S \cap C_s^j = \{v, z \}$. By Proposition 2.4, we can find a notation, such that $u_x< v_x< w_x < z_x$. Moreover, $v_x - u_x < {s \over 2}$ and $w_x - v_x < {s \over 2}$. Suppose that S admits a vertex, say a, in $C_s^k$ for some $k \in [i,j]_t$. We may assume w.l.o.g. that $u_x< a_x < v_x$. Since $a_y \in [u_y,v_y]_t$ and $a_x \in [u_x,v_x]_s$, it follows that a belongs to a shortest u, v-path and we obtain a contradiction. $\square$

Let u, v, and w be vertices of $V(C_s \Box C_t)$. We say that u attacks w (together with v) if $d(u,v) + d(v,w) = d(u,w)$.

Proposition 2.6

Let $s \ge t \ge 4$, $a, b, c \in V(C_s \Box C_t)$, $a \in V(C_s^i)$ and $b,c \in V(C_s^{j})$, such that $j \in [i,k]_t$ for some $i,k \in [t]_0$. If $a_x \in [b_x, c_x]_s$, then a attacks (together with b or c) a vertex $d\in V(C_s^{k})$ if and only if $d_x \in ([s]_0\setminus [b_x, c_x]_s ) \cup \{b_x, c_x\}$.

Proof

We may assume w.l.o.g. that $a_x = \lfloor {s \over 2} \rfloor$, $k>i$, $b_x < a_x$ and $k-i \le {t \over 2}$. If $d_x \le a_x$, then by Claim 1.2, we have $I(a,d) = \{ (x,y) \; | \; x \in [a_x, d_x] \; \textrm{and} \; y \in [i, k]_t \}$. Moreover, $b \in I(a,d)$ if and only if $d_x \le b_x$. Since the proof for $d_x \ge a_x$ is analogous, the assertion follows. $\square$

Proposition 2.7

Let $s \ge t \ge 4$, $i,j,k \in [t]_0$, $i\not = j$, $|k-i|_t = \lfloor {t \over 2} \rfloor$ and $j \in [i,k]_t$. If S is a general position set in $C_s \Box C_t$, such that $|S \cap C_s^i|=|S \cap C_s^j|=2$, then $|S \cap C_s^{\ell }|=0$ for every $\ell \in [i,k]_t \setminus \{i,j\}$.

Proof

We may assume w.l.o.g. that $i\le \lfloor {t \over 2} \rfloor$, $j>i$ and $j-i\le \lfloor {t \over 2} \rfloor$. It follows that $k = i + \lfloor {t \over 2} \rfloor$. Let S be a general position set in $C_s \Box C_t$, such that $S \cap C_s^i = \{u, w \}$ and $S \cap C_s^{j} = \{v, z \}$. By Proposition 2.5, we have that $|S \cap C_s^{\ell }|=0$ for every $\ell \in [i+1,j-1]$. Thus, we have to show that $|S \cap C_s^{\ell }|=0$ for every $\ell \in [j+1,i + \lfloor {t \over 2}\rfloor ]$.

By Proposition 2.4, we can find a notation, such that $u_x< v_x< w_x < z_x$. We claim that every vertex of $V(C_s^{\ell })$ is attacked by a vertex of $\{u, w \}$. Suppose to the contrary that $V(C_s^{\ell })$ admits a vertex, say a, which is not attacked by a vertex of $\{u, w \}$. We may assume w.l.o.g. that $u_x< a_x < v_x$. By Proposition 2.6, w attacks (together with v or z), all vertices of $V(C_s^{\ell })$ with the exception of those having first coordinate in $[v_x+1, z_x-1]$. Since $a_x \not \in [v_x+1, z_x-1]$, we obtain a contradiction. $\square$

Theorem 2.8

If $s \ge 4$, then $gp(C_s \Box C_4) = 5$.

Proof

By Lemma 3.3, we have to show that $gp(C_s \Box C_4) \le 5$. Assume to contrary that S is a general position set of $C_s \Box C_4$ with six vertices. By Proposition 2.2, $|S \cap C_s^i|\le 2$ for every $i \in [4]_0$. Since $|S|=6$, there exist $i,j \in [4]$, $i \not = j$, such that $|S \cap V(C_s^i)| = |S \cap V(C_s^j)| =2$. Note that we may assume that either $j=i+1$ or $j=i+2$ (modulo t). If $j=i+2$, then by Proposition 2.7, we have $|S \cap C_s^{i+1}|=|S \cap C_s^{i-1}|=0$ and we obtain a contradiction. Similarly, if $j=i+1$, then $|S \cap C_s^{i+2}|=|S \cap C_s^{i-1}|=0$ and we again obtain a contradiction.

This assertion completes the proof. $\square$

Theorem 2.9

If $s \ge 5$, then $gp(C_s \Box C_5) = 6$.

Proof

By Theorem 1.1, we have to show that $gp(C_s \Box C_5) \le 6$. Assume to contrary that S is a general position set with seven vertices. By Proposition 2.2, it holds that $|S \cap C_s^i|\le 2$ for every $i \in [5]$. Since $|S|=7$, there exist $i,j \in [5]$, $i \not = j$, such that $|S \cap V(C_s^i)| = |S \cap V(C_s^j)| =2$. Note that we may assume that either $j=i+1$ or $j=i+2$ (modulo s).

If $j=i+1$, then by Proposition 2.7, we have $|S \cap C_s^{i+2}|=|S \cap C_s^{i-1}|=0$. Since it follows that $|S \cap C_s^{i+3}| =3$, Proposition 2.2 yields a contradiction.

If $j=i+2$, then $|S \cap C_s^{i+1}| =0$ by Proposition 2.5. It follows that $|S \cap C_s^{i+2}| =2$ or $|S \cap C_s^{i-1}| =2$. Since we showed above that S cannot admit four vertices in two consecutive copies of $C_s$, we again obtain a contradiction.$\square$

The following proposition follows from Claim 1.2.

Proposition 2.10

Let S be a general position set of $C_s \Box C_t$, $s \ge t \ge 4$, and $i \not = j$. If $\{ a, b, c \} \subseteq S$, such that $a,b \in C_s^i$, $c \in C_s^j$, $a_x< c_x < b_x$, $c_x -a_x \le {s \over 2}$ and $b_x -c_x \le {s \over 2}$, then $|S \cap [a_x,b_x] \times [a_y,c_y]_t|=3$.

Theorem 2.11

If $s \ge 6$, then $gp(C_s \Box C_6) = 6$.

Proof

By Theorem 1.1, we have to show that $gp(C_s \Box C_6) \le 6$. Assume to contrary that S is a general position set with seven vertices. By Proposition 2.2, we have $|S \cap C_s^i|\le 2$ for every $i \in [6]_0$. Since $|S|=7$, there exists at least one $i \in [6]_0$, such that $|S \cap V(C_s^i)| =2$. Suppose w.l.o.g. that $i=2$.

In addition, suppose first that there exists $j \in [6]_0$, $j > i$, such that $|S \cap V(C_s^j)| =2$. Note that we may assume $j-i \le 3$. By Proposition 2.7, we have $|S \cap V(C_s^k)| \not = 0$, $k \not \in \{ i,k \}$, only if $j=4$ and $k=0$. Since $|S \cap C_s^k|\le 2$, it follows that $|S|<7$ and we obtain a contradiction.

Thus, we may conclude that $|S \cap V(C_s^j)| =1$ for every $j \not = i$. Let $S \cap V(C_s^2) = \{a, b\}$ and $S \cap V(C_s^5) = \{c\}$. Assume w.l.o.g. that $a_x< c_x < b_x$. We can see that $c_x - a_x < {s \over 2}$ and $b_x - c_x < {s \over 2}$, since otherwise $b \in I(a,c)$ or $c \in I(a,b)$. By Proposition 2.10, we have $|S \cap [a_x,b_x] \times [6]_0|=3$. Thus, for every $d \in S{\setminus } \{a, b, c\}$ we have $d_x \in [s]_0{\setminus }[a_x, b_x]$. Let $d \in V(C_s^4)$. We can show analogously as above that $|a_x - d_x| < {s \over 2}$ and $|b_x - d_x| < {s \over 2}$. We may therefore apply (slightly modified) Proposition 2.10 to see that $|S \cap ([s]_0\setminus [a_x,b_x]) \times [2,4]|=3$. It follows that S does not admit a vertex in $V(C_s^3)$ and we obtain a contradiction. $\square$

3 General Construction

Let a, b be positive integers and let $s^{a,b}= (s^{a,b}_0, s^{a,b}_1, s^{a,b}_2, s^{a,b}_3, s^{a,b}_4, s^{a,b}_5, s^{a,b}_6)$ be the 7-tuple of integer pairs defined as

$s^{a,b} {:}{=} ((0,0),(a,2b),(2a, 4b), (3a, 6b),(4a,b),(5a,3b),(6a,5b))$. Let also $s^{a,b}_{i,x}$ and $s^{a,b}_{i,y}$, $i \in [7]_0$ denote the first and the second coordinate of $s^{a,b}_{i}$, respectively.

We may consider the set that comprises the coordinates (integer pairs) of $s^{a,b}$ as a subset of $V(C_{7a} \Box C_{7b})$. Moreover, we can show that $s^{a,b}$ forms a general position set in $C_{7a} \Box C_{7b}$.

Proposition 3.1

Let a and b be positive integers. Then, $s^{a,b}$ is a general position set in $C_{7a} \Box C_{7b}$.

Proof

To see that the elements of

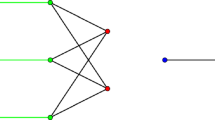
$s^{1,1}=((0,0),(1,2),(2, 4), (3, 6),(4,1),(5,3),(6,5))$ form a general position set of $C_{7} \Box C_{7}$, note that for every $i,j \in [7]_0$, $i \not =j$, we have $d_{C_{7} \Box C_{7}}(s^{1,1}_i,s^{1,1}_j) \in \{3, 4, 5\}$. The graph $C_{7} \Box C_{7}$ with the vertices of $s^{1,1}$ can be seen on the left-hand side of Fig. 2.

By the definition of $s^{a,b}$, for every $i \in [7]_0$, it holds that $s^{a,b}_{i,x} = a s^{1,1}_{i,x}$ and $s^{a,b}_{i,y} = b s^{1,1}_{i,y}$. Suppose now that $s^{a,b}_{k} \in I(s^{a,b}_{i},s^{a,b}_{j})$ for some $i,j,k \in [7]_0$. By Claim 1.2, we have $s^{a,b}_{k,x} \in [s^{a,b}_{i,x}, s^{a,b}_{j,x}]_{7a}$ and, therefore, $a s^{1,1}_{k,x} \in [a s^{1,1}_{i,x}, a s^{1,1}_{j,x}]_{7a}$ which in turn implies $s^{1,1}_{k,x} \in [s^{1,1}_{i,x}, s^{1,1}_{j,x}]_{7}$. Analogously, from $s^{a,b}_{k,y} \in [s^{a,b}_{i,y}, s^{a,b}_{j,y}]_{7b}$, it follows that $s^{1,1}_{k,y} \in [s^{1,1}_{i,y}, s^{1,1}_{j,y}]_{7}$. However, since the vertices of $s^{1,1}$ form a general position set in $C_{7} \Box C_{7}$, for every $i,j,k \in [7]_0$, it holds that $s^{1,1}_{k,x} \not \in [s^{1,1}_{i,x}, s^{1,1}_{j,x}]_{7}$ or $s^{1,1}_{k,y} \not \in [s^{1,1}_{i,y}, s^{1,1}_{j,y}]_{7}$ and we obtain a contradiction. $\square$

Fig. 2

$s^{1,1}$ in $C_{7} \Box C_{7}$ (left) and $s^{1,1} + ^{3}\!\delta ^{x}$ in $C_{10} \Box C_{7}$ (right)

To find a more general construction, we first define the following six 7-tuples of integer pairs with zero second coordinate:

$^{1}\!\delta ^{x} {:}{=} ((0,0),(0,0),(0, 0), (1, 0),(1,0),(1,0),(1,0))$, $^{2}\!\delta ^{x} {:}{=} ((0,0),(0,0),(0, 0), (1, 0),(2,0),(2,0),(2,0))$, $^{3}\!\delta ^{x} {:}{=} ((0,0),(0,0),(1, 0), (2, 0),(3,0),(3,0),(3,0))$, $^{4}\!\delta ^{x} {:}{=} ((0,0),(0,0),(1, 0), (2, 0),(3,0),(4,0),(4,0))$, $^{5}\!\delta ^{x} {:}{=} ((0,0),(1,0),(2, 0), (3, 0),(4,0),(5,0),(5,0))$, $^{6}\!\delta ^{x} {:}{=} ((0,0),(1,0),(2, 0), (3, 0),(4,0),(5,0),(6,0))$. Furthermore, we define six 7-tuples of integer pairs with zero first coordinate:

$^{1}\!\delta ^{y} {:}{=} ((0,0),(0,0),(0, 1), (0, 1),(0,0),(0,1),(0,1))$, $^{2}\!\delta ^{y} {:}{=} ((0,0),(0,0),(0, 1), (0, 2),(0,0),(0,1),(0,1))$, $^{3}\!\delta ^{y} {:}{=} ((0,0),(0,1),(0, 2), (0, 3),(0,0),(0,2),(0,2))$, $^{4}\!\delta ^{y} {:}{=} ((0,0),(0,1),(0, 2), (0, 4),(0,0),(0,2),(0,3))$, $^{5}\!\delta ^{y} {:}{=} ((0,0),(0,2),(0, 3), (0, 5),(0,1),(0,3),(0,4))$, $^{6}\!\delta ^{y} {:}{=} ((0,0),(0,2),(0, 4), (0, 6),(0,1),(0,3),(0,5))$. For a convenience, let $^{0}\delta ^{x}=^{0}\!\delta ^{y}{:}{=} ((0,0),(0,0),(0, 0), (0, 0),(0,0),(0,0),(0,0))$.

Let a, b be positive integers. If $i,j\in [7]_0$, then the addition $s^{a,b} + ^{i}\!\delta ^{x} + ^{j}\!\delta ^{y}$ is determined in a natural way, i.e., the k-th coordinate of the resulted 7-tuple is equal to $s^{a,b}_k + ^{j}\!\!\delta ^{x}_k + ^{j}\!\!\delta ^{y}_k$ for every $k\in [7]_0$. For $i \in [6]$, we write $s^{a,b} + ^{i}\!\!\delta ^{x} + ^{0}\!\!\delta ^{y}$ (resp. $s^{a,b} + ^{0}\!\!\delta ^{x} + ^{i}\!\!\delta ^{y}$) also as $s^{a,b} + ^{i}\!\!\delta ^{x}$ (resp. $s^{a,b} + ^{i}\!\!\delta ^{y}$).

Note that the integer pairs of $s^{a,b} + ^{i}\!\!\delta ^{x} + ^{j}\!\!\delta ^{y}$ correspond to the vertices of $C_{7a+i} \Box C_{7b+j}$ for every $i,j\in [6]$. Thus, we will call a 7-tuple $s^{a,b} + ^{i}\!\!\delta ^{x} + ^{j}\!\!\delta ^{y}$ “the vertices“ (in $C_{7a+i} \Box C_{7b+j}$). As an example, observe the vertices defined by $s^{1,1} + ^{3}\!\delta ^{x}$ in $C_{10} \Box C_{7}$ on the right-hand side of Fig. 2.

The following proposition was verified by a computer.

Proposition 3.2

Let $i\in [6]$. Then, the vertices of $s^{1,1} + ^{i}\!\!\delta ^{x}$ form a general position set in $C_{7+i} \Box C_{7}$.

Remark

Let $j\in [6]$. The vertices of $s^{1,1} + ^{j}\!\!\delta ^{y}$ do not form a general position set in $C_{7} \Box C_{7+j}$, while, on the other hand, the vertices of $s^{1,2} + ^{j}\!\!\delta ^{y}$ form a general position set in $C_{14} \Box C_{7+j}$.

If s is a positive integer and $x_i, d_i \in [s]_0$ for every $i \in [s]_0$, then s-tuples $(x_0, x_1, \ldots ,x_{s-1})$ and $(d_0, d_2, \ldots ,d_{s-1})$ are said to be stable, if the values in $(x_0, x_1, \ldots ,x_{s-1})$ are pairwise distinct and, for every $i,j \in [s]_0$, it holds that $x_i < x_j$ if and only if $d_i \le d_j$.

Note that if a is an integer, then for every $i\in [s]_0$, we have $ax_i + d_i < as + d$, where $d = \max _{i\in [s]}\{d_i\}$.

We will need the following result.

Proposition 3.3

Let $(x_0, x_1, \ldots ,x_{s-1})$ and $(d_0, d_2, \ldots ,d_{s-1})$ be stable s-tuples for an odd s and let $d = \max _{i\in [s]}\{d_i\}$. If $a\ge b \ge s$ are integers and $bx_i + d_i \not \in [bx_j+d_j,bx_k+d_k]_{bs+d}$ for some $i,j,k \in [s]_0$, then $ax_i + d_i \not \in [ax_j+d_j,ax_k+d_k]_{as+d}$.

Proof

We may suppose w.l.o.g. that $bx_k+d_k > bx_j+d_j$. Since $(x_0, x_1, \ldots ,x_{s-1})$ and $(d_0, d_2, \ldots ,d_{s-1})$ are stable, we have $x_k > x_j$ and $d_k \ge d_j$. Moreover, from $bx_i + d_i \not \in [bx_j+d_j,bx_k+d_k]_{bs+d}$, it follows that $bx_k+d_k - bx_j-d_j \not = \frac{bs+d}{2}$.

If $bx_k+d_k - bx_j - d_j < \frac{bs+d}{2}$, then we show first that $x_k - x_j < \frac{s}{2}$. Assume to the contrary that $x_k - x_j > \frac{s}{2}$. Then, remind that s is odd, $b(x_k - x_j) + d_k - d_j \ge \frac{bs+b}{2} + d_k - d_j$. Since $d_k \ge d_j$ and $b > d$, we have $\frac{bs+b}{2} + d_k - d_j \ge \frac{bs+b}{2} > \frac{bs+d}{2}$ and we obtain a contradiction.

We next show that from $bx_k+d_k - bx_j - d_j < \frac{bs+d}{2}$, it follows that $ax_k+d_k - ax_j - d_j < \frac{as+d}{2}$. Let $c {:}{=} a - b$. Since $x_k - x_j < \frac{s}{2}$, we have $a(x_k - x_j) + d_k - d_j = b(x_k - x_j) + c(x_k - x_j) + d_k - d_j < \frac{bs+d}{2} + c(x_k - x_j) \le \frac{bs+d}{2} + \frac{cs}{2} = \frac{as+d}{2}$.

By the assumption that $bx_i + d_i \not \in [bx_j+d_j,bx_k+d_k]_{bs+d}$, we have either $bx_i + d_i < bx_j+d_j$ or $bx_i + d_i > bx_k+d_k$. If $bx_i + d_i < bx_j+d_j$, then, since $(x_0, x_1, \ldots ,x_{n-1})$ and $(d_0, d_2, \ldots ,d_{n-1})$ are s-stable, it holds that $ax_i + d_i < ax_j+d_j$. Since, for $bx_i + d_i > bx_k+d_k$, we obtain $ax_i + d_i > ax_k+d_k$, it follows that $ax_i + d_i \not \in [ax_j+d_j,ax_k+d_k]_{as+d}$.

The proof for $bx_k+d_k - bx_j- d_j > \frac{bs+d}{2}$ is analogous. $\square$

Theorem 3.4

If t and s are integers with $s \ge t \ge 4$, then

$$\begin{aligned} gp(C_s \Box C_t) = \left\{ \begin{array}{llll} 5, &{} t = 4 \\ 6, &{} t \in \{5, 6\} \; \textrm{or } \; s, t \in \{8, 10, 12 \}\\ 7, &{} \; \textrm{otherwise } \\ \end{array}. \right. \end{aligned}$$

Proof

If $t \in \{4, 5, 6\}$, Theorems 2.8, 2.9 and 2.11 yield the assertion.

We verified with a computer that the vertices of $s^{a,b} + ^{i}\!\!\delta ^{x} + ^{j}\!\!\delta ^{y}$ form a general position set in $C_{7a+i} \Box C_{7b+j}$ for every $a \in [7]$, $b \in [2,7]$ and $i,j \in [7]_0$.

Assume now that $t,s \ge 49$ and let positive integers a and b be determined in a way that $t=7b+i$ and $s=7a+j$, where $i,j \in [7]_0$. We will show that the vertices of $s^{a,b} + ^{i}\!\!\delta ^{x} + ^{j}\!\!\delta ^{y}$ form a general position set in $C_s \Box C_t$.

More precisely, we will show that for every $i_1,i_2,i_3 \in [7]_0$ we have $s^{a,b}_{i_1} \not \in I(s^{a,b}_{i_2},s^{a,b}_{i_3})$. By Claim 3.3, we have to show $s^{a,b}_{i_1,x} + ^{i}\!\!\delta ^{x}_{i_1,x} \not \in [s^{a,b}_{i_2,x} + {^{i}\!\delta ^{x}_{i_2,x}}, s^{a,b}_{i_3,x} + ^{i}\!\!\delta ^{x}_{i_3,x}]_{s}$ or $s^{a,b}_{i_1,y} + ^{i}\!\!\delta ^{y}_{i_1,y} \not \in [s^{a,b}_{i_2,y} + ^{i}\!\!\delta ^{y}_{i_2,y}, s^{a,b}_{i_3,y} + ^{i}\!\!\delta ^{y}_{i_3,y}]_{t}$. Since the vertices of $s^{7,7} + ^{i}\!\!\delta ^{x} + ^{j}\!\!\delta ^{y}$ form a general position set in $C_{49+i} \Box C_{49+j}$, we have $s^{7,7}_{i_1,x} + ^{i}\!\!\delta ^{x} \not \in [s^{7,7}_{i_2,x}+ ^{i}\!\!\delta ^{x}_{i_2,x}, s^{7,7}_{i_3,x}+ ^{i}\!\!\delta ^{x}_{i_2,x}]_{49+i}$ or $s^{7,7}_{i_1,y} + ^{i}\!\!\delta ^{y} \not \in [s^{7,7}_{i_2,y}+ ^{i}\!\!\delta ^{y}_{i_2,y}, s^{7,7}_{i_3,y}+ {^{i}\!\delta ^{y}_{i_2,y}}]_{ 49+i}$.

Note that $s^{7,7}_{i_1,x} + ^{i}\!\delta ^{x}_{i_1,x} \not \in [s^{7,7}_{i_2,x}+ ^{i}\!\delta ^{x}_{i_2,x}, s^{7,7}_{i_3,x}+ ^{i}\!\delta ^{x}_{i_2,x}]_{49+i}$ (resp. $s^{7,7}_{i_1,y} + {^{i}\!\delta ^{y}_{i_1,y}} \not \in [s^{7,7}_{i_2,y}+ ^{i}\!\delta ^{y}_{i_2,y}, s^{7,7}_{i_3,y}+ ^{i}\!\delta ^{x}_{i_2,y}]_{49+i}$) if and only if $7\,s^{1,1}_{i_1,x} + ^{i}\!\delta ^{x}_{i_1,x} \not \in [7\,s^{1,1}_{i_2,x}+ {^{i}\!\delta ^{x}_{i_2,x}}, 7\,s^{1,1}_{i_3,x}+ ^{i}\!\delta ^{x}_{i_2,x}]_{49+i}$ (resp. $7\,s^{1,1}_{i_1,y} + {^{i}\!\delta ^{y}_{i_1,y}} \not \in [7\,s^{1,1}_{i_2,y}+ {^{i}\!\delta ^{y}_{i_2,y}}, 7\,s^{1,1}_{i_3,y}+ ^{i}\!\delta ^{y}_{i_2,x}]_{49+i}$).

Since the 7-tuples $(s^{1,1}_{0,x},\ldots , s^{1,1}_{6,x})$ and $(^{i}\!\delta ^{x}_{0,x},\ldots , ^{i}\!\delta ^{x}_{6,x})$ (resp. $(s^{1,1}_{0,y},\ldots , s^{1,1}_{6,y})$ and $(^{i}\!\delta ^{y}_{0,y},\ldots , ^{i}\!\delta ^{x}_{6,y})$) are stable and $a,b \ge 7$, from Proposition 3.3, it follows that if $s^{7,7}_{i_1,x} + ^{i}\!\delta ^{x}_{i_1,x} \not \in [s^{7,7}_{i_2,x}+ ^{i}\!\delta ^{x}_{i_2,x}, s^{7,7}_{i_3,x}+ ^{i}\!\delta ^{x}_{i_2,x}]_{49+i}$, then $a s^{1,1}_{i_1,x} + ^{i}\!\delta ^{x}_{i_1,x} \not \in [a s^{1,1}_{i_2,x}+ ^{i}\!\delta ^{x}_{i_2,x}, a s^{1,1}_{i_3,x}+ ^{i}\!\delta ^{x}_{i_2,x}]_{7a+i}$. Moreover, if $s^{7,7}_{i_1,y} + ^{i}\!\delta ^{y}_{i_1,y} \not \in [s^{7,7}_{i_2,y}+ ^{i}\!\delta ^{y}_{i_2,y}, s^{7,7}_{i_3,y}+ {^{i}\!\delta ^{y}_{i_2,y}}]_{49+i}$, then $b s^{1,1}_{i_1,y} + ^{i}\!\delta ^{y}_{i_1,y} \not \in [b s^{1,1}_{i_2,y}+ ^{i}\!\delta ^{y}_{i_2,y}, b s^{1,1}_{i_3,y}+ ^{i}\!\delta ^{y}_{i_2,y}]_{7b+j}$.

Thus, the proof for $s,t \ge 49$ is complete.

For the remaining cases, note first that by Proposition 3.2 the vertices of $s^{1,1} + ^{i}\!\!\delta ^{x}$ form a general position set in $C_{7+i} \Box C_{7}$ for every $i \in [6]$.

For other graphs of interest, we used a reduction to SAT to find general position sets using a computer. The applied approach is described in the next section.

In particular, we determined that a general position set with seven vertices does not exist for the graphs $C_8 \Box C_{8}$, $C_{10} \Box C_8$, $C_{12} \Box C_{8}$, $C_{10} \Box C_{10}$, $C_{12} \Box C_{10}$ and $C_{12} \Box C_{12}$. From Theorem 1.1, then it follows that $gp(C_s \Box C_t) = 6$ if $s, t \in \{8, 10, 12 \}$.

Moreover, we found general position sets with seven vertices for the graphs $C_9 \Box C_{8}$, $C_{11} \Box C_{8}$, $C_{13} \Box C_{8}$, $C_9 \Box C_{9}$, $C_{10} \Box C_{9}$, $C_{11} \Box C_{9}$, $C_{12} \Box C_{9}$, $C_{13} \Box C_{9}$, $C_{11} \Box C_{10}$, $C_{13} \Box C_{10}$, $C_{11} \Box C_{11}$, $C_{12} \Box C_{11}$, $C_{13} \Box C_{11}$, $C_{13} \Box C_{12}$, and $C_{13} \Box C_{13}$, which can be obtained on the web page https://omr.fnm.um.si/wp-content/uploads/2017/06/GP-Cartesian-two-cycles.txt.

Since we have established the existence of a general position set with seven vertices for every graph of interest, the proof is complete. $\square$

4 Hypercubes

The problem of finding the size of the largest general position set in $Q_n$ is known to be equivalent to finding the largest size of a so-called $(2, 1)-$separating system in coding theory. Within this setting, the value of

$$\begin{aligned} \alpha = {\lim _{ h \rightarrow \infty } \sup }\frac{\log _2 gp(Q_h)}{h} \end{aligned}$$

was considered in [6, 11]. In particular, it is shown that

$$\begin{aligned} \alpha \ge \frac{3}{50} \log _2 11. \end{aligned}$$

(1)

This result, however, does not improve the following simple lower bound on general position number of $Q_h$ if $h \le 21$.

Proposition 4.1

If $h \ge 3$, then every hypercube of dimension h admits a general position set of cardinality $h+1$.

Proof

Let $S' = \{0^i10^{h-i-1} \; | \; i \in [h]_0 \}$ and $S = S' \cup \{ 1^h \}$. Note that for every pair $u,v \in S'$, we have $d_{Q_h}(u,v)=2$. Moreover, since, for every $u \in S'$, we have $d_{Q_h}(u,1^h)=h-1$, S is a general position set in $Q_h$. $\square$

Table 1 Lower bounds and exact values on $gp(Q_h)$

Based on the above discussion, we try to answer the question of whether the lower bound on the general position number can be improved for hypercubes of (at least) moderate dimensions.

We applied a reduction from the problem of finding a general position set in a graph to the satisfiability problem. The method had been successfully applied for distance constrained coloring problems for various finite and infinite graphs. See for example [7, 12], where these concepts were used for the packing coloring problem and radio labeling, respectively.

We implemented two approaches for constructing propositional formulas that correspond to the general position set with k vertices in a graph of order n. In both approaches, we used Cryptominisat5 [3] to find the solutions of the derived propositional formulas.

First, we took a general approach with $n \cdot k$ Boolean variables $x_{i,j}$, $i \in [n], j \in [k]$. In this approach, two types of propositional formulas are formed: the first set of formulas ensure that for every $j \in [k]$, at least one $x_{i,j}$ is chosen, while the second set of formulas specify that for every triple of vertices, at most two vertices are chosen if one of the vertices belongs to a shortest path connecting the other two.

The described reduction was first applied to obtain general position sets in the Cartesian product of two cycles of moderate lengths (the obtained sets helped us to devise results from the previous sections). On the other hand, this approach turned out to be less successful for hypercubes due to the fact that the number of vertices of a hypercube $Q_h$ grows exponentially with respect to h. The consequence is an exponential growth of the number of the corresponding Boolean variables and propositional formulas. For this reason, the approach becomes infeasible for a desktop computer if the dimension of a hypercube exceeds 8.

Hence, we devised a purpose-built approach for hypercubes, which for a triple of vertices $u=u_1, \ldots , u_h, v=v_1, \ldots , v_h, w=w_1, \ldots , w_h \in V(Q_h)$ uses the fact that w does not belong to a shortest u, v-path in $Q_h$ if and only if for at least one $i \in [h]$ we have $w_i \not = u_i = v_i$. This observation enables us to construct propositional formulas with $h \cdot k$ informatory boolean variables which are used (together with $3h {k \atopwithdelims ()3}$ additional variables) to transform the above condition to the set of $O(h k^3)$ clauses in conjunctive normal form.

The described approach enabled us to compute general position sets in hypercubes of dimensions up to 24. Computations were performed with a desktop computer (with at most 15 independent threads) and a high-performance computer (which allows up to 128 independent threads). The cardinalities of the largest general position sets for these graphs are presented in Table 1. For the hypercubes of dimensions less or equal to seven, the presented values indicate exact values on the general position number, since we could confirm that general position sets with greater cardinality for these graphs do not exist. For the hypercubes of larger dimensions, the cardinalities of obtained general position sets significantly improve the lower bounds on the general position number of $Q_h$ derived from Proposition 4.1 and in Eq. (1).

Since $Q_h$ is isomorphic to $P_2^{\Box ,h}$, it is worthwhile to mention that $P_{\infty }^{\Box ,h} = 2^{2^{h-1}}$, where $P_{\infty }$ denotes the two-way infinite path, as shown in [5].