1 Introduction

A tiling of a convex body \({\mathcal {K}}\) in Euclidean d-space \({\mathbb {R}}^d\) is a finite family of compact sets in \({\mathbb {R}}^d\) with mutually disjoint interiors, called tiles, whose union is \({\mathcal {K}}\). A tiling is monohedral if all tiles are congruent.

In this paper, we deal with the monohedral tilings of the closed circular unit disc \({\mathcal {B}}^2\) with center O, in which the tiles are Jordan regions, i.e., are homeomorphic to a closed circular disc. The easiest way to generate such tilings, which we call rotationally generated tilings, is to rotate around O a simple curve connecting O to a point on the boundary \({\mathcal {S}}^1\) of \({\mathcal {B}}^2\), where by a curve we mean a continuous map of the interval [0, 1] to the Euclidean plane. The following question, based on the observation that any tile of such a monohedral tiling of \({\mathcal {B}}^2\) contains O, seems to arise regularly in recreational mathematical circles [13].

Question 1

Are there monohedral tilings of \({\mathcal {B}}^2\) in which not all of the tiles contain O?

The answer to Question 1 is affirmative; the usual examples to show this are the first two configurations in Fig. 1. The following harder variant is attributed to Stein by Croft, Falconer and Guy in [2, last paragraph on p. 87].

Question 2

(Stein). Are there monohedral tilings of \({\mathcal {B}}^2\) in which O is in the interior of a tile?

A systematic investigation of monohedral tilings of \({\mathcal {B}}^2\) was started in [7] by Haddley and Worsley. In their paper, they called a monohedral tiling radially generated, if every tile is radially generated, meaning that its boundary is a simple curve consisting of three parts: a circular arc of length \(\alpha \) and two other curves one of which is the rotation of the other one about their common point by angle \(\alpha \in (0,2\pi )\). Furthermore, they called a monohedral tiling a subtiling if it is obtained by replacing the tiles by monohedral tilings. The following ambitious conjecture appears in [7, Conjecture 6.1; for more details see conjectures 6.2 and 6.3 too].

Conjecture 1

(Haddley and Worsley). Every monohedral tiling is a subtiling of a radially generated tiling.

It is worth noting that while every rotationally generated tiling is radially generated, the converse does not necessarily hold, see Fig. 1.

A similar problem was investigated in [6] by Goncharov, who, for any O-symmetric convex body in \({\mathbb {R}}^d\), determined the smallest number of congruent copies of a subset of the body that cover the body. In the spirit of this approach, we raise the following variant of Question 1:

Question 3

What is the minimum cardinality \(n({\mathcal {B}}^2)\) of a monohedral tiling of \({\mathcal {B}}^2\) in which not all of the tiles contain O?

As the configurations in Fig. 1 show, we have \(n({\mathcal {B}}^2) \le 12\). On the other hand, the lower bound \(n({\mathcal {B}}^2) \ge 3\) is also relatively easy to prove: it was posed as a problem in 2000 on the Russian Mathematical Olympiads [3]. Presently, to the authors’ knowledge, the best bounds on \(n({\mathcal {B}}^2)\) are still the trivial ones: \(3 \le n({\mathcal {B}}^2) \le 12\).

Fig. 1
figure 1

A non-radially (It may be worth noting that this configuration also appears regularly in various places: this was chosen, for example, as the logo of the MASS program at Penn State University, it appears on the front page of five issues of the Hungarian problem-solving mathematical journal Középiskolai Matematikai Lapok [16], and it can be found also in the book [2, Figure C8].), a radially, and a rotationally generated monohedral tiling of \({\mathcal {B}}^2\). In contrast to these three, the rightmost, radially generated monohedral tiling is not rotationally invariant

Full size image

Our main result is the following.

Theorem 1.1

Any monohedral tiling of \({\mathcal {B}}^2\) with at most three topological discs is rotationally generated.

This result implies Conjecture 1 for tilings with at most 3 tiles, yields the first nontrivial lower bound for \(n({\mathcal {B}}^2)\), and, in particular, proves that the answer for Question 2 is refuting for tilings with at most three tiles.

Corollary 1.2

We have \(n({\mathcal {B}}^2) \ge 4\).

Corollary 1.3

There is no monohedral tiling of \({\mathcal {B}}^2\) with at most three topological discs as tiles, such that the center of \({\mathcal {B}}^2\) is contained in exactly one of them.

In Sect. 2, we introduce the notions used in the paper, investigate the basic properties of monohedral tilings of \({\mathcal {B}}^2\), and prove a series of lemmas that we use in the proof of Theorem 1.1. In Sect. 3, we prove Theorem 1.1.

Finally, in Sect. 4, we collect our additional remarks and propose some open problems.

2 Notations and Preliminaries

Throughout the proof, we denote by \({\mathcal {B}}^2\) the closed unit circular disc with the origin \(O=(0,0)\) as its center, and its boundary by \({\mathcal {S}}^1={{\,\mathrm{\partial }\,}}{\mathcal {B}}^2\). We say that two points \(P,Q \in {\mathcal {S}}^1\) are antipodal if \(d(P,Q) = 2\), where \(d(\cdot , \cdot )\) denotes Euclidean distance. For points \(P,Q \in {\mathbb {R}}^2\), the closed segment with endpoints P, Q is denoted by \({\overline{PQ}}\).

For any \(P,Q \in {\mathbb {R}}^2\) with \(d(P,Q) \le 2r\), the r-spindle \(\ominus ^r_{P,Q}\) of two points P, Q is by definition (see [1] or [4]) the intersection of all Euclidean discs of radius \(r>0\) that contain P and Q. In other words, \(\ominus ^r_{P,Q}\) is the region bounded by the two circular arcs of radius \(r>0\) that connect P and Q and are not longer than a half-circle.

A set homeomorphic to \({\mathcal {B}}^2\) is called a topological disc. The boundary of a topological disc is a simple, closed curve, called Jordan curve.

If the boundary \({{\,\mathrm{\partial }\,}}{\mathcal {D}}\) of a topological disc \({\mathcal {D}}\) contains a unit circular arc \({\mathcal {C}}\), then for every relative interior point P of \({\mathcal {C}}\), there is some \(\varepsilon > 0\), such that the open neighborhood of P of radius \(\varepsilon \) intersects \({{\,\mathrm{\partial }\,}}{\mathcal {D}}\) only in points of \({\mathcal {C}}\). Such a neighborhood is divided into two open components by \({\mathcal {C}}\) exactly one of which belongs to \({\mathcal {D}}\). If the component belonging to \({\mathcal {D}}\) is the one contained in the interior of the unit circle containing \({\mathcal {C}}\) in its boundary, then clearly independently from the choice of P, we say that \({\mathcal {C}}\) is a convex circular arc of \({\mathcal {D}}\), and in the opposite case that it is a concave circular arc of \({\mathcal {D}}\).

The Jordan–Schoenflies theorem [17] yields that every Jordan curve is the boundary of a topological disc. We remark that since all topological discs are compact, they are Lebesgue measurable; we denote their measure by \({{\,\mathrm{area}\,}}(\cdot )\). Nevertheless, there are topological discs (see, e.g., the Koch snowflake, or for more examples [15]) whose boundary is not rectifiable. Our next lemma, which we use in the proof, holds for these topological discs, as well.

Lemma 2.1

Let \(\Gamma \) be a Jordan curve and \({\mathcal {C}}\) be a simple curve. Then, \(\Gamma \) contains only finitely many congruent copies of \({\mathcal {C}}\) that are mutually disjoint, apart from possibly their endpoints.

Proof

Assume for contradiction that \(\Gamma \) contains infinitely many congruent copies \({\mathcal {C}}_n\) \((n=1,2,\ldots )\) of \({\mathcal {C}}\) which are mutually disjoint, apart from possibly their endpoints. Let \(P_n\) and \(Q_n\) denote the endpoints of \({\mathcal {C}}_n\). Since \(\Gamma \) is compact, we may assume that \(\lim _{n \rightarrow \infty } P_n = P\) and \(\lim _{n \rightarrow \infty } Q_n =Q\) for some \(P,Q \in \Gamma \). By the properties of congruence, \(P \ne Q\). On the other hand, since \(\Gamma \) is homeomorphic to \({\mathcal {S}}^1\), the congruent copies of \({\mathcal {C}}\) correspond to mutually non-overlapping circular arcs on \({\mathcal {S}}^1\). Clearly, this implies that \(P=Q\), a contradiction. \(\square \)

Lemma 2.2

Let \({\mathcal {D}}= {\mathcal {D}}_1 \cup {\mathcal {D}}_2\), where \({\mathcal {D}}, {\mathcal {D}}_1\) and \({\mathcal {D}}_2\) are topological discs, and \({{\,\mathrm{int}\,}}{\mathcal {D}}_1 \cap {{\,\mathrm{int}\,}}{\mathcal {D}}_2 = \emptyset \). Then, \({\mathcal {S}}_1 = {\mathcal {D}}_1 \cap {{\,\mathrm{\partial }\,}}{\mathcal {D}}\), \({\mathcal {S}}_2 = {\mathcal {D}}_2 \cap {{\,\mathrm{\partial }\,}}{\mathcal {D}}\), and \({\mathcal {S}}={{\,\mathrm{\partial }\,}}{\mathcal {D}}_1 \cap {{\,\mathrm{\partial }\,}}{\mathcal {D}}_2\) are simple curves.

Proof

As \({\mathcal {D}}\) is a topological disc, we have a homeomorphism \(\chi \), such that \(\chi ({\mathcal {D}})={\mathcal {B}}^2\). Since the statement of the lemma is topologically invariant, it is sufficient to prove it in the case \({\mathcal {D}}= {\mathcal {B}}^2\). Thus, we may assume that \({\mathcal {S}}_i={\mathcal {S}}^1\cap {\mathcal {D}}_i\) for \(i=1,2\), where we observe that since \({\mathcal {D}}_i\) and \({\mathcal {S}}^1\) are closed, so is \({\mathcal {S}}_i\).

First, we show that \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\) are connected. Assume, for example, that some \(X_1, Y_1 \in {\mathcal {S}}_1\) cannot be connected by an arc in \({\mathcal {S}}_1\). Then, there are some points \(X_2, Y_2 \notin {\mathcal {S}}_1\) that separate \(X_1\) and \(Y_1\) in \({\mathcal {S}}^1\). Clearly, we have \(X_2, Y_2 \in {\mathcal {S}}_2\). For any \(i=1,2\), since \({\mathcal {D}}_i\) is a topological disc, there is a simple curve \(\gamma _i\) with endpoints \(X_i, Y_i\), such that apart from these points, \(\gamma _i\) is contained in \({{\,\mathrm{int}\,}}{\mathcal {S}}_i\). By continuity, \(\gamma _1 \cap \gamma _2 \ne \emptyset \), implying that \({{\,\mathrm{int}\,}}{\mathcal {D}}_1 \cap {{\,\mathrm{int}\,}}{\mathcal {D}}_2 \ne \emptyset \), a contradiction. Thus, \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\) are connected, which yields that they are closed circular arcs in \({\mathcal {S}}^1\). Let the (common) endpoints of these arcs be P and Q.

The points \(P,Q\in {\mathcal {S}}_1\cap {\mathcal {S}}_2\) are also in \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_1\cap {{\,\mathrm{\partial }\,}}{\mathcal {D}}_2\), and hence, they are connected by a simple curve in \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_1{\setminus }{\mathcal {S}}_1\) and also in \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_2{\setminus }{\mathcal {S}}_2\). These curves coincide, because \({\mathcal {D}}={\mathcal {D}}_1\cup {\mathcal {D}}_2\), and hence, it is \({\mathcal {S}}\), and the proof of Lemma 2.2 is complete. \(\square \)

Lemma 2.3

Let \(\{ {\mathcal {D}}_1, {\mathcal {D}}_2, {\mathcal {D}}_3 \}\) be a tiling of the topological disc \({\mathcal {D}}\), where for \(i=1,2,3\), \({\mathcal {D}}_i\) is a topological disc, such that \({\mathcal {S}}_i={\mathcal {D}}_i \cap {{\,\mathrm{\partial }\,}}{\mathcal {D}}\) is a non-degenerate simple curve. Then, \({\mathcal {D}}_1 \cap {\mathcal {D}}_2 \cap {\mathcal {D}}_3\) is a singleton \(\{ M \}\), and for any \(i \ne j\), \({\mathcal {D}}_i \cap {\mathcal {D}}_j\) is a simple curve connecting M and a point in \({{\,\mathrm{\partial }\,}}{\mathcal {D}}\).

Proof

Suppose for contradiction that there are two distinct points \(M_1, M_2 \in {\mathcal {D}}_i\) for \(i=1,2,3\). For any i, let \(\Gamma _i\) be a simple curve connecting \(M_1\) and \(M_2\) which is contained in \({{\,\mathrm{int}\,}}{\mathcal {D}}_i\), apart from \(M_1\) and \(M_2\). Note that for any \(i \ne j\), \(\Gamma _i \cup \Gamma _j\) is a simple, closed curve. Thus, the union of a pair of the curves, say \(\Gamma _1 \cup \Gamma _2\) encloses the third one. This implies that \(\Gamma _1 \cup \Gamma _2\) encloses \({\mathcal {D}}_3\). Since \(M_1, M_2 \notin {\mathcal {S}}^1\) by our conditions, it follows that \({\mathcal {D}}_3\) is disjoint from \({\mathcal {S}}^1\); a contradiction. Thus, \({\mathcal {D}}_1 \cap {\mathcal {D}}_2 \cap {\mathcal {D}}_3\) contains at most one point. On the other hand, since the closure \({\mathcal {X}}_1\) of \(({{\,\mathrm{\partial }\,}}{\mathcal {D}}_1) {\setminus } {\mathcal {S}}_1\) is a simple, connected curve and it can be decomposed into the closed sets \({\mathcal {X}}_1 \cap {\mathcal {D}}_2\) and \({\mathcal {X}}_1 \cap {\mathcal {D}}_3\), it follows that these sets intersect, that is \({\mathcal {D}}_1 \cap {\mathcal {D}}_2 \cap {\mathcal {D}}_3\) is not empty. Thus, \({\mathcal {D}}_1 \cap {\mathcal {D}}_2 \cap {\mathcal {D}}_3 = \{ M \}\) for some \(M \in {{\,\mathrm{int}\,}}{\mathcal {D}}\).

To prove the second part of Lemma 2.3, we may apply an argument like in the proof of Lemma 2.2. \(\square \)

By the circumcircle of a topological disc \({\mathcal {D}}\), we mean the unique smallest closed Euclidean circle encompassing \({\mathcal {D}}\). The convex hull of the circumcircle is the circumdisc of \({\mathcal {D}}\), and the radius of the circumcircle is the circumradius of \({\mathcal {D}}\). Observe that the center of the circumcircle \({\mathcal {C}}\) of \({\mathcal {D}}\) is in \({{\,\mathrm{conv}\,}}({\mathcal {C}}\cap {\mathcal {D}})\), as, otherwise, a smaller circle would encompass \({\mathcal {D}}\).

Lemma 2.4

Assume that \({\mathcal {S}}^1\) is the circumcircle of both of the non-overlapping congruent topological discs \({\mathcal {D}}_1\) and \({\mathcal {D}}_2\). Then, there is a diameter \({\overline{PQ}}\) of \({\mathcal {B}}^2\) separating \({\mathcal {S}}_1 = {\mathcal {D}}_1 \cap {\mathcal {S}}^1\) and \({\mathcal {S}}_2 = {\mathcal {D}}_2 \cap {\mathcal {S}}^1\). Furthermore, any congruence g with \(g({\mathcal {D}}_1) = {\mathcal {D}}_2\) is either the reflection about the line of \({\overline{PQ}}\), or the reflection about O.

Proof

Using the idea of the proof of Lemma 2.2, it follows that there are no pairs of points \(X_1, Y_1 \in {\mathcal {S}}_1\) and \(X_2, Y_2 \in {\mathcal {S}}_2\) that strictly separate each other on \({\mathcal {S}}^1\). In other words, there is a line \(\ell \) separating \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\). On the other hand, as \(O\in {{\,\mathrm{conv}\,}}{\mathcal {S}}_1\cap {{\,\mathrm{conv}\,}}{\mathcal {S}}_2\), \(\ell \) contains O and \(\ell \cap {\mathcal {S}}^1 \subseteq {\mathcal {S}}_1 \cap {\mathcal {S}}_2\), proving the first statement with \(\{ P,Q \} = \ell \cap {\mathcal {S}}^1\). We note that from this argument it also follows that \({\mathcal {S}}_1 \cap {\mathcal {S}}_2 = \{ P,Q \}\).

Consider some isometry g with \(g({\mathcal {D}}_1) = {\mathcal {D}}_2\). The uniqueness of the circumcircle clearly implies that \(g({\mathcal {S}}^1) = {\mathcal {S}}^1\), and thus, \(g (\{ P, Q \}) = \{ P, Q \}\). This implies that g is either the reflection about the line of \({\overline{PQ}}\), the reflection about the line bisecting \({\overline{PQ}}\), or the reflection about O. We show that the conditions of the lemma exclude the second case: Consider a simple curve \(\Gamma \) from P to Q, such that \(\Gamma {\setminus } \{ P, Q \} \subset {{\,\mathrm{int}\,}}{\mathcal {D}}_1\). Then, at least one point R of \(\Gamma \) lies on the line \(\ell ^{\perp }\) bisecting \({\overline{PQ}}\). If g is the reflection about \(\ell ^{\perp }\), then \(g(R) = R\), and hence, \(R \in {{\,\mathrm{int}\,}}{\mathcal {D}}_1 \cap {{\,\mathrm{int}\,}}{\mathcal {D}}_2\); a contradiction. \(\square \)

In the remaining part of Section 2, we deal only with a monohedral tiling of \({\mathcal {B}}^2\), where the tiles \({\mathcal {D}}_i\), \(i=1,2,\ldots ,n\), are congruent copies of a topological disc \({\mathcal {D}}\). For any \(j \ne 1\), we fix an isometry \(g_{1j}\) mapping \({\mathcal {D}}_1\) into \({\mathcal {D}}_j\), and for any values of i, j, we set \(g_{ij}=g_{1i}^{-1} \circ g_{1j}\). Then, by definition, we have \(g_{ji}=g_{ij}^{-1}\) for all values of i, j. Finally, we set \({\mathcal {S}}_i = {\mathcal {D}}_i \cap {\mathcal {S}}^1\) for all values of i.

Lemma 2.5

If \({\mathcal {D}}\) contains two points at the distance 2, then \(n=1\) or \(n=2\), and the tiling is rotationally generated.

Proof

If \({\mathcal {D}}\) contains two points at the distance 2, then each tile contains two antipodal points of \({\mathcal {B}}^2\). Thus, \({\mathcal {B}}^2\) is the circumdisc of each tile, which implies that \(g_{ij}({\mathcal {B}}^2)={\mathcal {B}}^2\) for all values of i, j. Since \(O \in {\mathcal {D}}_i\) for some value of i, it also yields that \(O \in {\mathcal {D}}_i\) for all values of i. Then, by Lemma 2.4, there is a diameter \({\overline{PQ}}\) of \({\mathcal {B}}^2\) whose endpoints belong to every tile, and the congruence between any two of them is either a reflection about the line through \({\overline{PQ}}\), or the reflection about the midpoint of \({\overline{PQ}}\). This implies that there are at most two tiles.

To prove that the tiling is rotationally generated, assume that \(n=2\), and \({\mathcal {D}}_2\) is a reflected copy of \({\mathcal {D}}_1\) about the line through \({\overline{PQ}}\). Since, in this case, \({\mathcal {D}}_1\) and \({\mathcal {D}}_2\) are the two closed half discs of \({\mathcal {B}}^2\) containing \({\overline{PQ}}\) in their boundaries, the statement follows. \(\square \)

Lemma 2.6

For all values of i, \({\mathcal {S}}_i\) \((i=1,\dots ,n)\) is a closed, connected arc in \({\mathcal {S}}^1\).

Proof

As \({\mathcal {S}}_1\) is compact, there are points \(P,Q\in {\mathcal {S}}_1\) farthest from each other in \({\mathcal {S}}_1\). If P, Q are antipodal points of \({\mathcal {S}}^1\), then every \({\mathcal {D}}_i=g_{1i}({\mathcal {D}}_1)\) (\(i=1,\ldots \)) contains antipodal points, and hence, \({\mathcal {B}}^2\) is the circumdisc of every tile. Then, Lemma 2.5 yields that \(n=1\) or \(n=2\). The case \(n=1\) is trivial, and if \(n=2\), then by Lemma 2.4, there is a diameter \({\overline{PQ}}\) separating \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\), which implies that \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\) are closed half-circles. Thus, we may assume that P, Q are not antipodal.

Let \(\Gamma \subset {\mathcal {S}}^1\) be the shorter arc connecting P and Q. We show that \(\Gamma \subset {\mathcal {D}}_1\).

For contradiction, suppose that a point \(X \in \Gamma \) does not belong to \({\mathcal {D}}_1\). Then, without loss of generality, we may assume that \(X \in {\mathcal {D}}_2\), and that \(X \ne P\), \(X \ne Q\).

Let \(r>0\) be the radius of the circumdisc \({\mathcal {B}}\) of \({\mathcal {D}}_1\). Since \({\mathcal {D}}_1\) is compact, and it does not contain antipodal points of \({\mathcal {S}}^1\), we have \(r < 1\), implying that \(\ominus ^r_{P,Q}\) contains \(\Gamma {\setminus }\{P,Q\}\) in its interior. Thus, \(\Gamma \subset {\mathcal {B}}\), and \(\Gamma {\setminus }\{P,Q\}\subset {{\,\mathrm{int}\,}}{\mathcal {B}}\). Let \(\Gamma '\) be a curve connecting P and Q, such that \(\Gamma ' {\setminus } \{P,Q\} \subset {{\,\mathrm{int}\,}}{\mathcal {D}}_1\). This yields that \(\Gamma \cup \Gamma '\) is a simple, closed curve in \({\mathcal {B}}\) enclosing \({\mathcal {D}}_2\). which, by the congruence of \({\mathcal {D}}_1\) and \({\mathcal {D}}_2\), implies that the \({\mathcal {B}}\) is the circumdisc of \({\mathcal {D}}_2\), as well. Hence, by Lemma 2.4, it follows that \({{\,\mathrm{conv}\,}}({{\,\mathrm{\partial }\,}}{\mathcal {B}}\cap {\mathcal {D}}_1 \cap {\mathcal {D}}_2)\) is a diameter \(\delta \) of \({\mathcal {B}}\). As P, Q are the only points of \(\Gamma \cup \Gamma '\) that may fall on \({{\,\mathrm{\partial }\,}}{\mathcal {B}}\), we have \(\delta = {\overline{PQ}}\).

From Lemma 2.4, it also follows that \(g_{12}\) is the reflection about the line of \({\overline{PQ}}\), or the reflection about the midpoint of \({\overline{PQ}}\), and in particular \(g_{21}=g_{12}\). On the other hand, observe that \(g_{12} ( \ominus ^1_{P,Q} ) = \ominus ^1_{P,Q} = {\mathcal {B}}^2 \cap g_{12}({\mathcal {B}}^2)\). Since \({\mathcal {D}}_1 \subset {\mathcal {B}}^2\) and \({\mathcal {D}}_1 = g_{12}({\mathcal {D}}_2) \subset g_{12}({\mathcal {B}}^2)\), this implies that \({\mathcal {D}}_1, {\mathcal {D}}_2 \subset \ominus ^1_{P,Q}\). Now, if there is a point \(R\in {\mathcal {D}}_2 \cap {{\,\mathrm{\partial }\,}}\ominus ^1_{P,Q}{\setminus } \Gamma \), then R and X can be connected with a curve in \({{\,\mathrm{int}\,}}{\mathcal {D}}_2\). This curve strictly separates \(P, Q \in {\mathcal {D}}_1\) in \(\ominus ^1_{P,Q}\), which can also be connected by a curve in \({{\,\mathrm{int}\,}}{\mathcal {D}}_1\). This contradicts our assumption that \({\mathcal {D}}_1\) and \({\mathcal {D}}_2\) have disjoint interiors. Hence, \( {\mathcal {D}}_2 \cap {{\,\mathrm{\partial }\,}}\ominus ^1_{P,Q}\subset \Gamma \), and accordingly, \({\mathcal {D}}_1\cap {\mathcal {S}}^1=\{P,Q\}\), and, in particular, \({\mathcal {D}}_1\cap \Gamma =\{P,Q\}\).

Assume that there is an interior point Y of \(\Gamma \) that belongs to, say, \({\mathcal {D}}_3\). Since \(P,Q \in {\mathcal {D}}_2\), we may repeat the argument in the previous paragraph, replacing \({\mathcal {D}}_1\) and \({\mathcal {D}}_2\) by \({\mathcal {D}}_2\) and \({\mathcal {D}}_3\), respectively, and obtain that \({\mathcal {D}}_2\cap \Gamma =\{P,Q\}\) contradicting our assumption that there is an interior point \(X\in {\mathcal {D}}_2\) of \(\Gamma \). Thus, \(\Gamma \subset {\mathcal {D}}_2\), which yields by Lemma 2.4 that \({\mathcal {D}}_2 \cap {\mathcal {S}}^1 = \Gamma \) and \(\ominus ^1_{P,Q}={\mathcal {D}}_1 \cup {\mathcal {D}}_2\). From this, in particular, it follows that \({{\,\mathrm{area}\,}}({\mathcal {D}}_1 ) = {{\,\mathrm{area}\,}}({\mathcal {D}}_2 ) = {{{\,\mathrm{area}\,}}(\ominus ^1_{P,Q})}/{2}\).

Since for all values of i, \(g_{2i}(\{ P,Q \}) \subset {\mathcal {B}}^2\), the definition of 1-spindle implies that \({\mathcal {D}}_i \subset \ominus ^1_{g_{2i}(P),g_{2i}(Q)} \subset {\mathcal {B}}^2\), and \(g_{2i}(\mathcal {\mathcal {D}}_2) {\setminus } \Gamma \subset {{\,\mathrm{int}\,}}\ominus ^1_{g_{2i}(P),g_{2i}(Q)}\) is disjoint from \({\mathcal {S}}^1\). In other words, the sets \(g_{2i}(\Gamma )\) cover \({\mathcal {S}}^1\). Note that these arcs may intersect each other only at their endpoints, and if \(|{\mathcal {S}}^1\cap g_{2i}(\Gamma )|\ge 3\), then \(g_{2i}(\Gamma )\subset {\mathcal {S}}^1\). Thus, \({\mathcal {S}}^1\) can be decomposed into finitely many, say \(k < n\) circular arcs, each of which is congruent to \(\Gamma \).

Let \(s={2\pi }/{k}\) denote the arclength of \(\Gamma \). Then, \(ks=2\pi \) on one hand, and

$$\begin{aligned} \frac{\pi }{n}=\frac{{{\,\mathrm{area}\,}}(B^2)}{n}={{\,\mathrm{area}\,}}({\mathcal {D}}_2) =\frac{{{\,\mathrm{area}\,}}(\ominus ^1_{P,Q})}{2}=\frac{s-\sin s}{2} =\frac{\frac{2\pi }{k}-\sin \frac{2\pi }{k}}{2}, \end{aligned}$$

on the other hand. Thus, we have \(\sin \frac{2\pi }{k}=2\pi (\frac{1}{k}-\frac{1}{n})\). The left-hand side is an algebraic number (see, e.g., [18, Theorem 2.1]), from which \(\frac{2}{k}=\frac{4}{n}\) follows, and hence, \(\sin \frac{2\pi }{k} = 0\), implying that k is a divisor of 2, contradicting our assumption that \(\Gamma \) is shorter than a half-circle. \(\square \)

Remark 2.7

Since \({\mathcal {S}}_i \subset {{\,\mathrm{\partial }\,}}{{\,\mathrm{conv}\,}}{\mathcal {D}}_i\), it follows that for all values of i, j, we have \(g_{ij}({\mathcal {S}}_i) \subset {{\,\mathrm{\partial }\,}}{{\,\mathrm{conv}\,}}{\mathcal {D}}_j\).

Remark 2.8

For any values of i, j, k, the arcs \(g_{ik}({\mathcal {S}}_i)\) and \(g_{jk}({\mathcal {S}}_j)\) share at most some of their endpoints, or they coincide.

Proof

Observe that since for any i, \({\mathcal {S}}_i\) is contained in the convex hull of \({\mathcal {D}}_i\), if the arcs \(g_{ik}({\mathcal {S}}_i)\) and \(g_{jk}({\mathcal {S}}_j)\) are not disjoint apart from (possibly) their endpoints, then \(g_{ik}({\mathcal {S}}_i) \cap g_{jk}({\mathcal {S}}_j)\) is a non-degenerate unit circular arc, and thus, \(g_{ik}({\mathcal {S}}_i) \cup g_{jk}({\mathcal {S}}_j)\) lies on a unit circle \({\mathcal {S}}\).

Since \({\mathcal {S}}_i = g_{ki} (g_{ik}({\mathcal {S}}_i)) \subset {\mathcal {S}}^1\), we have \(g_{ki} ({\mathcal {S}}) = {\mathcal {S}}^1\). Thus, \({\mathcal {S}}_i \cup g_{ki} (g_{jk}({\mathcal {S}}_j)) \subset {\mathcal {S}}^1 \cap {\mathcal {D}}_ i = {\mathcal {S}}_i\). This implies that \(g_{jk}({\mathcal {S}}_j) \subseteq g_{ik}({\mathcal {S}}_i)\). The containment relation \(g_{ik}({\mathcal {S}}_i) \subseteq g_{jk}({\mathcal {S}}_j)\) can be obtained using a similar argument, which yields the desired equality. \(\square \)

Lemma 2.9

Let \({\mathcal {D}}_1, {\mathcal {D}}_2, \dots ,{\mathcal {D}}_n\) be a monohedral tiling of \({\mathcal {B}}^2\), where \(n > 1\). Then, at least two of the arcs \({\mathcal {S}}_1\), \(g_{21}({\mathcal {S}}_2)\), \(\dots \), \(g_{n1}({\mathcal {S}}_n)\) coincide.

Proof

Suppose for contradiction that the arcs \({\mathcal {S}}_1, g_{21}({\mathcal {S}}_2), \ldots , g_{n1}({\mathcal {S}}_n)\) are disjoint apart from possibly their endpoints. By our earlier observation, these arcs are in \({{\,\mathrm{\partial }\,}}{{\,\mathrm{conv}\,}}{\mathcal {D}}_1\). As the total turning angle of these n arcs is \(2\pi \), and the total turning angle along the boundary of a convex body is also \(2\pi \), \({{\,\mathrm{\partial }\,}}{{\,\mathrm{conv}\,}}{\mathcal {D}}_1\) may only consist in excess of these arcs some segments that connect the endpoints of these arcs in a smooth way. In other words, \({{\,\mathrm{conv}\,}}{\mathcal {D}}_1={\mathcal {P}}+{\mathcal {B}}^2\) for some convex n-gon \({\mathcal {P}}\). This implies that the circumradius of \({\mathcal {D}}_1\) is at least 1, with equality if and only if \({\mathcal {D}}_1 ={\mathcal {B}}^2\), a contradiction. \(\square \)

Definition 2.10

A multicurve (see also [11]) is a finite family of simple curves, called the members of the multicurve, which are parameterized on non-degenerate closed finite intervals, and any point of the plane belongs to at most one member, or it is the endpoint of exactly two members. If \({\mathcal {F}}\) and \({\mathcal {G}}\) are multicurves, \(\bigcup {\mathcal {F}}= \bigcup {\mathcal {G}}\), and every member of \({\mathcal {F}}\) is the union of some members of \({\mathcal {G}}\), we say that \({\mathcal {G}}\) is a partition of \({\mathcal {F}}\).

Definition 2.11

Let \({\mathcal {F}}\) and \({\mathcal {G}}\) be multicurves. If there are partitions \({\mathcal {F}}'\) and \({\mathcal {G}}'\) of \({\mathcal {F}}\) and \({\mathcal {G}}\), respectively, and a bijection \(f:{\mathcal {F}}' \rightarrow \mathcal {G'}\), such that \(f({\mathcal {C}})\) is congruent to \({\mathcal {C}}\) for all \({\mathcal {C}}\in {\mathcal {F}}'\), we say that \({\mathcal {F}}\) and \({\mathcal {G}}\) are equidecomposable.

The following lemma can be proved very similarly to the analogous statement for equidecomposability of polygons [5], and thus, we omit the proof.

Lemma 2.12

Equidecomposability is an equivalence relation on the family of multicurves in \({\mathbb {R}}^2\).

Corollary 2.13

If \({\mathcal {F}}\) and \({\mathcal {G}}\) are multicurves with \(\bigcup {\mathcal {F}} = \bigcup {\mathcal {G}}\), then \({\mathcal {F}}\) and \({\mathcal {G}}\) are equidecomposable.

Proof

Clearly, it is sufficient to prove the statement for the connected components of \(\bigcup {\mathcal {F}}\), and by Lemma 2.12, we may assume that one of the multicurves, say \({\mathcal {G}}\), is a simple curve. But then, \({\mathcal {F}}\) is a partition of \({\mathcal {G}}\), in which case the statement is obvious. \(\square \)

Corollary 2.14

If \({\mathcal {F}}\) and \({\mathcal {G}}\) are equidecomposable, and their subfamilies \({\mathcal {F}}' \subseteq {\mathcal {F}}\) and \({\mathcal {G}}' \subseteq {\mathcal {G}}\) are equidecomposable, then \({\mathcal {F}}{\setminus }{\mathcal {F}}'\) and \({\mathcal {G}}{\setminus }{\mathcal {G}}'\) are equidecomposable.

Proof

By Lemma 2.12, we may assume that \(\bigcup {\mathcal {F}} = \bigcup {\mathcal {G}}\). Without loss of generality, we may also assume that \(\bigcup {\mathcal {F}}\) is connected, which yields that we may regard both \({\mathcal {F}}\) and \({\mathcal {G}}\) as different partitions of the same simple curve. More specifically, after reparametrizing if necessary, we may assume that there is some curve \({\mathcal {C}}:[a,b] \rightarrow {\mathbb {R}}^2\), and partitions \(P_F\) and \(P_G\) of [a, b], such that the elements of \({\mathcal {F}}\) and \({\mathcal {G}}\) are the restrictions of \({\mathcal {C}}\) to the subintervals of \(P_F\) and \(P_G\), respectively. By Corollary 2.13, a multicurve is equidecomposable with any of its partitions, and hence, we may assume that \(P_F = P_G\), and there is a bijection between the elements of \(\mathcal {F'}\) and \(\mathcal {G'}\), such that the corresponding elements are congruent. Since congruence is an equivalence relation, it is clear that any such bijection can be extended to all subintervals of \(P_F\), which proves the assertion. \(\square \)

3 Proof of Theorem 1.1

First, consider a monohedral tiling of \({\mathcal {B}}^2\) with the topological discs \({\mathcal {D}}_1\) and \({\mathcal {D}}_2\). The containment \(O \in {\mathcal {D}}_1 \cap {\mathcal {D}}_2\) can be proved in a number of elementary ways (see, e.g., [8]); here, we also show that the tiling is rotationally generated.

By Lemma 2.6, for \(i=1,2\), \({\mathcal {S}}_i = {\mathcal {D}}_i \cap {\mathcal {S}}^1\) is a connected arc, and hence, \({\mathcal {S}}_1\) or \({\mathcal {S}}_2\) is an arc of length at least \(\pi \). Thus, \({\mathcal {D}}_1\) or \({\mathcal {D}}_2\) contains a pair of antipodal points of \({\mathcal {B}}^2\), which, by Lemma 2.5, implies that the tiling is rotationally generated.

From now on, we consider the case that \({\mathcal {B}}^2\) is decomposed into three congruent topological discs \({\mathcal {D}}_1, {\mathcal {D}}_2, {\mathcal {D}}_3\), and for \(i=1,2,3\), we set \({\mathcal {S}}_i = {\mathcal {D}}_i \cap {\mathcal {S}}^1\). By Lemmas 2.6 and 2.5, we may assume that each tile intersects \({\mathcal {S}}^1\) in a non-degenerate circle arc, which is smaller than a half-circle.

By Lemma 2.3, we have that \({\mathcal {D}}_1 \cap {\mathcal {D}}_2 \cap {\mathcal {D}}_3\) consists of a single point \(M \in {{\,\mathrm{int}\,}}{\mathcal {B}}^2\), and that for any \(i \ne j\), \({\mathcal {D}}_i \cap {\mathcal {D}}_j\) is a simple curve connecting M and a point of \({\mathcal {S}}^1\).

To prove the assertion, we distinguish some cases. Before we do it, we observe that by Remark 2.8, any pair of the curves \({\mathcal {S}}_1\), \(g_{21}({\mathcal {S}}_2)\), and \(g_{31}({\mathcal {S}}_3)\) intersect in at most a common endpoint, or they coincide.

Case 1 No pair of the arcs \({\mathcal {S}}_1\), \(g_{21}({\mathcal {S}}_2)\), and \(g_{31}({\mathcal {S}}_3)\) coincide.

In this case, we immediately have a contradiction by Lemma 2.9.

Case 2 Two of the arcs \({\mathcal {S}}_1\), \(g_{21}({\mathcal {S}}_2)\) and \(g_{31}({\mathcal {S}}_3)\) coincide, and the third one is different

Using a suitable relabeling of the tiles, we may assume that \({\mathcal {S}}_1 = g_{21}({\mathcal {S}}_2)\). Let the arclength of this arc be \(0< \alpha < \pi \), and the arclength of \({\mathcal {S}}_3\) be \(\beta \). The equality \({\mathcal {S}}_1 = g_{21}({\mathcal {S}}_2)\) implies, in particular, that \(g_{21}\) is an isometry of \({\mathcal {S}}^1\); or more generally that it is either the reflection about the symmetry axis \(\ell \) of \({\mathcal {S}}_1 \cup {\mathcal {S}}_2\) or a rotation around O with angle \(\alpha \). We may assume without loss of generality that \(\ell \) is the y-axis, the common point of \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\) is (0, 1), and \({\mathcal {S}}_1\subset \{(x,y):x\le 0\}\). Furthermore, in the proof, we set \({\mathcal {C}}_1 = {\mathcal {D}}_1 \cap {\mathcal {D}}_3\), and \({\mathcal {C}}_2 = {\mathcal {D}}_2 \cap {\mathcal {D}}_3\).

Subcase 2.a \(g_{21}\) is the reflection about \(\ell \).

If there is a point \(P\in {{\,\mathrm{int}\,}}{\mathcal {D}}_1\cap \{(x,y):x>0\}\), then a curve \(\Gamma \) in \({{\,\mathrm{int}\,}}{\mathcal {D}}_1\) connects P and the midpoint of \({\mathcal {S}}_1\), so \(g_{12}(\Gamma )\) connects the midpoint of \({\mathcal {S}}_2\) to \(g_{12}(P)\) in \({{\,\mathrm{int}\,}}{\mathcal {D}}_2\). This implies that \(\Gamma \cap g_{12}(\Gamma )\) is in \({{\,\mathrm{int}\,}}{\mathcal {D}}_1\cap {{\,\mathrm{int}\,}}{\mathcal {D}}_2=\emptyset \), which is a contradiction. Thus, we have \({\mathcal {D}}_1\subset \{(x,y):x\le 0\}\) and also \({\mathcal {D}}_2\subset \{(x,y):x\ge 0\}\).

Observe that \(g_{13}({\mathcal {S}}_1)=g_{23}(g_{12}({\mathcal {S}}_1)) = g_{23}({\mathcal {S}}_2)\), and \({\mathcal {D}}_3={{\,\mathrm{cl}\,}}(\mathcal {\mathcal {B}}^2 {\setminus } ({\mathcal {D}}_1 \cup {\mathcal {D}}_2))\) is symmetric in \(\ell \). We denote this arc of length \(\alpha \) by \({\mathcal {S}}=g_{13}({\mathcal {S}}_1)\). Note that by the conditions of Case 2, \({\mathcal {S}}\ne {\mathcal {S}}_3\), and \({\mathcal {S}}\subset {{\,\mathrm{\partial }\,}}{{\,\mathrm{conv}\,}}{\mathcal {D}}_3\) by Remark 2.7. Furthermore, \({{\,\mathrm{\partial }\,}}{{\,\mathrm{conv}\,}}{\mathcal {D}}_3\) does not contain any arc of length \(\alpha \) apart from \({\mathcal {S}}\) and possibly \({\mathcal {S}}_3\), as otherwise the idea of the proof of Lemma 2.9 yields a contradiction. Indeed, if \({{\,\mathrm{\partial }\,}}{{\,\mathrm{conv}\,}}{\mathcal {D}}_3\) contains two unit circular arcs of length \(\alpha \) and one unit circular arc of length \(\beta \) with mutually disjoint relative interiors, then the fact that \(2\alpha +\beta = 2\pi \) is equal to the total turning angle of \({{\,\mathrm{\partial }\,}}{{\,\mathrm{conv}\,}}{\mathcal {D}}_3\) yields that \({{\,\mathrm{\partial }\,}}{{\,\mathrm{conv}\,}}{\mathcal {D}}_3\) is the union of these arcs and possible some straight line segments, which contradicts our assumption that \({\mathcal {D}}_3\) is a proper subset of \({\mathcal {B}}^2\). Thus, \({\mathcal {S}}\) is symmetric in the y-axis.

Since \({\mathcal {D}}_3\) is connected, and every point of \(\ell \) belongs either to \({\mathcal {D}}_3\), or to both \({\mathcal {D}}_1\) and \({\mathcal {D}}_2\), the segment connecting the midpoint X of \({\mathcal {S}}\) and the midpoint Y of \({\mathcal {S}}_3\) belongs to \({\mathcal {D}}_3\). Let the length of \({\overline{XY}}\) be \(\delta > 0\), and note that the fact \(X,Y \in {{\,\mathrm{\partial }\,}}{{\,\mathrm{conv}\,}}{\mathcal {D}}_3\) yields that the line through \({\overline{XY}}\) intersects \({\mathcal {D}}_3\) exactly in \({\overline{XY}}\) and \({\overline{XY}} {\setminus } \{ X,Y \} \subset {{\,\mathrm{int}\,}}{\mathcal {D}}_3\). For \(i=1,2\), \(g_{3i}({\overline{XY}})\) is the segment of length \(\delta \) in \({\mathcal {B}}^2\), starting at the midpoint of \({\mathcal {S}}_i\), and perpendicular to it. Thus, if \(\delta < 1\), then \(O \notin {\mathcal {D}}_i\) for any value of i, if \(\delta > 1\), then \(O \in {{\,\mathrm{int}\,}}{\mathcal {D}}_i\) for all values of i, and if \(\delta = 1\), then O is the midpoint of a unit circle arc in the boundary of each of the \({\mathcal {D}}_i\)s, which is a contradiction.

Subcase 2.b \(g_{21}\) is the rotation around O by angle \(\alpha \) in counterclockwise direction.

As O is a fixed point of \(g_{21}\), it follows that either \(O \in {\mathcal {D}}_1 \cap {\mathcal {D}}_2\), or \(O \notin {\mathcal {D}}_1 \cup {\mathcal {D}}_2\). By the definition of tiling and our assumptions, in the first case, \(O \in {{\,\mathrm{\partial }\,}}{\mathcal {D}}_1 \cap {{\,\mathrm{\partial }\,}}{\mathcal {D}}_2\), and in the second case, \(O \in {{\,\mathrm{int}\,}}{\mathcal {D}}_3\).

First, consider the case that \(O \in {{\,\mathrm{\partial }\,}}{\mathcal {D}}_1 \cap {{\,\mathrm{\partial }\,}}{\mathcal {D}}_2\).

Recall that by Lemma 2.3, \(D_1 \cap D_2 \cap D_3\) is a single point M, and for any \(i \ne j\), \({\mathcal {D}}_i \cap {\mathcal {D}}_j\) is a simple curve connecting M to a point of \({\mathcal {S}}^1\). Thus, if \(O=M\), then \(g_{21}({\mathcal {D}}_1 \cap {\mathcal {D}}_2) = {\mathcal {D}}_1 \cap {\mathcal {D}}_3\), and \(g_{12}({\mathcal {D}}_1 \cap {\mathcal {D}}_2) = {\mathcal {D}}_2 \cap {\mathcal {D}}_3\). Since \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_1\) and \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_3\) are equidecomposable, this implies that \({\mathcal {S}}_1\) and \({\mathcal {S}}_3\) are congruent, and hence, \(\alpha = {2\pi }/{3}\). In other words, if \(O=M\), then the tiling is rotationally generated. Thus, we assume that \(O \notin {\mathcal {D}}_3\), which, by the compactness of \({\mathcal {D}}_3\), yields the existence of a small closed circular disc \({\mathcal {B}}\) centered at O, such that \({\mathcal {B}}\cap {\mathcal {D}}_3 = \emptyset \). Let \(t\mapsto {\mathcal {C}}(t)\) be a continuous parameterization of the curve \({\mathcal {D}}_1 \cap {\mathcal {D}}_2\) satisfying \(O={\mathcal {C}}(0)\), and let \(t_{+}=\sup \{t:{\mathcal {C}}([0,t]))\subset {\mathcal {B}}\}\) and \(t_{-}=\inf \{t:{\mathcal {C}}([t,0])\subset {\mathcal {B}}\}\). Then, \(g_{12}({\mathcal {C}}(t_\pm ))={\mathcal {C}}(t_\mp )\), which implies that \(g_{12}\) is the reflection about O. Thus, \(\alpha =\pi \) and \(\beta = 0\), which contradicts our assumptions.

In the remaining part of Subcase 2.b, we assume that \(O\in {{\,\mathrm{int}\,}}{\mathcal {D}}_3\).

Let \(M_1=g_{21}(M)\) and \(M_2=g_{12}(M)\). Since \(\alpha > 0\), we have \(M_2 \ne M\). On the other hand, we clearly have \(M_2 \in {{\,\mathrm{\partial }\,}}{\mathcal {D}}_2\) and \(M_2 \notin {\mathcal {S}}^1\).

Let \({\mathcal {B}}\) be the circular disc in \({\mathcal {D}}_3\) that is centered at O and is of maximum radius \(r>0\). Then, \({\mathcal {B}}\) is tangent to at least one of the curves \({\mathcal {C}}_1\) and \({\mathcal {C}}_2\), say \({\mathcal {C}}_2\) touches \({\mathcal {B}}\) in \(X_2\in {{\,\mathrm{\partial }\,}}{\mathcal {B}}\cap {\mathcal {C}}_2\). Let \(X_1=g_{21}(X_2)\). Then, \(X_1 \in {\mathcal {B}}\cap {\mathcal {D}}_1={\mathcal {B}}\cap {\mathcal {C}}_1\) clearly, and hence, \(X_2\in g_{12}({\mathcal {C}}_1)\cap {\mathcal {C}}_2\ne \emptyset \). Since \(g_{12}({\mathcal {C}}_1)\) is a curve in \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_2\), connecting the intersection point of \({\mathcal {S}}_1\) and \({\mathcal {S}}_2\) to \(M_2\) in \({{\,\mathrm{int}\,}}{\mathcal {B}}^2\), it follows that \(M \in g_{12}({\mathcal {C}}_1)\); that is, \(M_1\in {\mathcal {C}}_1\), implying also \(M_2 \in {\mathcal {C}}_2\).

Thus, \(M_1\) divides the curve \({\mathcal {C}}_1\) into two parts: one from M to \(M_1\), which we denote by \({\mathcal {C}}_1^M\), and the other one from \(M_1\) to a point of \(S_1\), which we denote by \({\mathcal {C}}_1^S\). We define the parts \({\mathcal {C}}_2^M\) and \({\mathcal {C}}_2^S\) of \({\mathcal {C}}_2\) similarly, using \(M_2\) in place of \(M_1\). Furthermore, we set \({\mathcal {C}}_3^S={\mathcal {D}}_1 \cap {\mathcal {D}}_2\).

We clearly have \(g_{21}({\mathcal {C}}_2^M) = {\mathcal {C}}_1^M\), \(g_{21}({\mathcal {C}}_2^S)={\mathcal {C}}_3^S\) and \(g_{21}({\mathcal {C}}_3^S)={\mathcal {C}}_1^S\). Observe that since \({\mathcal {D}}_1, {\mathcal {D}}_2\) and \({\mathcal {D}}_3\) are congruent, their boundaries are equidecomposable. Furthermore, as \({\mathcal {C}}_1^S\), \({\mathcal {C}}_2^S\), and \({\mathcal {C}}_3^S\), and also \({\mathcal {C}}_1^M\) and \({\mathcal {C}}_2^M\) are congruent, we obtain by Corollary 2.14 that \({\mathcal {S}}_1\) and \({\mathcal {C}}_1^M \cup {\mathcal {S}}_3\) are equidecomposable. Thus, we deduce that \({\mathcal {C}}_1^M\) (and also \({\mathcal {C}}_2^M\)) is a multicurve, such that its every member curve is a unit circular arc, and their total length is \(\alpha - \beta \ge 0\).

Let x and y denote the total length of the convex and concave unit circular arcs of \({\mathcal {D}}_1\) in \({\mathcal {C}}_1^M\). Since \({\mathcal {C}}_1^M\) and \({\mathcal {C}}_2^M\) are congruent, the total length of the convex and concave unit circular arcs of \({\mathcal {D}}_2\) in \({\mathcal {C}}_2^M\) is also x and y, respectively. Thus, since, for \(i \ne j\), a unit circular arc in \({\mathcal {D}}_i \cap {\mathcal {D}}_j\) is a convex circular arc of exactly one of \({\mathcal {D}}_i\) and \({\mathcal {D}}_j\) and concave for the other, the total length of the convex and concave unit circular arcs of \({\mathcal {D}}_3\) in \({\mathcal {C}}_1^M\cup {\mathcal {C}}_2^M\) is 2y and 2x, respectively.

The congruence of the tiles \({\mathcal {D}}_i\) and the curves \({\mathcal {C}}_i^S\) for \(i=1,2,3\) yields that the total lengths of the convex and concave unit circular arcs of \({\mathcal {D}}_1\) in \({\mathcal {S}}_1 \cup {\mathcal {C}}_1^M\) is equal to the total lengths of the convex and the concave unit circular arcs of \({\mathcal {D}}_3\) in \({\mathcal {S}}_3 \cup {\mathcal {C}}_1^M \cup {\mathcal {C}}_2^M\), respectively. This equality for convex circular arcs implies that \(\alpha + x = \beta + 2y\), and the equality for concave arcs implies \(y = 2x\). From these equations, it follows that \(x = (\alpha -\beta )/3\) and \(y=2(\alpha -\beta )/3\). Thus, in particular, it follows that if \(\beta = \alpha \), then \(x=y=0\) and \(M = M_1 =M_2\), which yields that \(\alpha = 0\), a contradiction. This means that \(\beta < \alpha \).

We show that M is not an interior point of a unit circular arc in \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_3\) longer than \(\alpha -\beta \). Suppose, for contradiction, that M is an interior point of such a circular arc \({\mathcal {C}}\). If one of \(M_1\) or \(M_2\), say, \(M_1 \in {\mathcal {C}}\), then \({\mathcal {C}}_1^M \subset {\mathcal {C}}\), which yields that \({\mathcal {C}}_2^M = g_{21}({\mathcal {C}}_1^M)\) is also a unit circular arc, implying that \({\mathcal {C}}_1^M \cup {\mathcal {C}}_2^M\) belongs to the same unit circle \({\hat{{\mathcal {S}}}}\). Since this circle is invariant under a rotation around O, we have \({\hat{{\mathcal {S}}}}={\mathcal {S}}^1\), which contradicts our assumption that \(M,M_1,M_2 \in {{\,\mathrm{int}\,}}{\mathcal {B}}^2\). Assume that \(M_1, M_2 \notin {\mathcal {C}}\), and let \({\mathcal {C}}^1\) and \({\mathcal {C}}^2\) denote \({\mathcal {C}}\cap {\mathcal {C}}_1^M\) and \({\mathcal {C}}\cap {\mathcal {C}}_2^M\), respectively. Then, \(g_{21}({\mathcal {C}}^2)\) is a unit circular arc in \({\mathcal {C}}_1^M\) whose length is equal to that of \({\mathcal {C}}^2\). Thus, since \({\mathcal {C}}\) is longer than \(\alpha -\beta \), \(g_{21}({\mathcal {C}}^2)\), and \({\mathcal {C}}^1\) intersect in a unit circular arc, which yields that \(g_{21}({\mathcal {C}}^2) \cup {\mathcal {C}}^1 = {\mathcal {C}}_1^M\) is a unit circular arc, leading to a contradiction in a similar way.

Let us say that a unit circular arc in \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_i\) is maximal, if it is not a proper subset of another unit circular arc in \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_i\). By Lemma 2.1, \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_1\) contains finitely many, say \(m \ge 1\) maximal unit circular arcs of length \(\alpha \), one of which is \({\mathcal {S}}_1\). Thus, \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_3\) also contains m maximal unit circular arcs of length \(\alpha \). By the previous paragraph, any of these arcs is contained in \({\mathcal {C}}_1^S \cup {\mathcal {C}}_1^M\) or in \({\mathcal {C}}_2^S \cup {\mathcal {C}}_2^M\). Assume that all these arcs are contained in \({\mathcal {C}}_1^S\) or in \({\mathcal {C}}_2^S\). Since \({\mathcal {C}}_1^S\), \({\mathcal {C}}_2^S\) and \({\mathcal {C}}_3^S\) are congruent, we have that the total number of unit circular arcs of length \(\alpha \) in \({\mathcal {C}}_i^S\) is equal to m/2. Thus, \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_1\) contains \(m+1\) arcs, which is a contradiction.

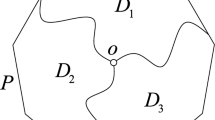
Finally, consider the case that some maximal unit circular arc \({\mathcal {S}}_{\alpha }\) of length \(\alpha \) in \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_3\) is not contained in \({\mathcal {C}}_1^S \cup {\mathcal {C}}_2^S\). Since \(\alpha > \alpha - \beta \), M is not an interior point of \({\mathcal {S}}_{\alpha }\), but \(M_1\) or \(M_2\) is. Without loss of generality, we may assume that \(M_1\) is in the interior of \({\mathcal {S}}_{\alpha }\). This implies that M is in the interior of \(g_{12}({\mathcal {S}}_{\alpha }) \subseteq {\mathcal {C}}_3^S \cup {\mathcal {C}}_2^M\) (similarly as Fig. 2 shows). Hence, M is not an interior point of a unit circular arc in \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_1\), which implies that \(M_2\) is not an interior point of any unit circular arc in \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_2\). On the other hand, again by Lemma 2.1, \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_3\) contains k maximal unit circular arcs of length \(\beta \) for some \(k \ge 1\), one of which is \({\mathcal {S}}_3\). By our previous argument, any of these arcs is contained in one of \({\mathcal {C}}_i^M\) or \({\mathcal {C}}_i^S\) for some \(i \in \{ 1,2 \}\). Let \(k_M \ge 0\) and \(k_S \ge 0\) denote the number of these arcs in \({\mathcal {C}}_1^M\) and \({\mathcal {C}}_1^S\), respectively. Then, \({\mathcal {C}}_1^M\) and \({\mathcal {C}}_1^S\) contain exactly \(k_M\) and \(k_S\) of these arcs, respectively. From this, it readily follows that \(k=2k_M+2k_S+1\). Furthermore, since \({{\,\mathrm{\partial }\,}}{\mathcal {D}}_1\) also contains k maximal unit circular arcs of length \(\beta \), we have \(k=k_M+2k_S\). This yields that \(k_M=-1\), which is a contradiction.

Fig. 2
figure 2

\({\mathcal {B}}^2\) is dissected into three topological discs

Full size image

Case 3 All of the arcs \({\mathcal {S}}_1\), \(g_{21}({\mathcal {S}}_2)\), and \(g_{31}({\mathcal {S}}_3)\) coincide.

In this case, \(g_{21}\) and \(g_{31}\) are either reflections about a line through O, or rotations around O. In particular, O is a fixed point of both of them, and thus, it is the unique common point M of all tiles. For any \(i \ne j\), let \({\mathcal {C}}_{ij} = {\mathcal {D}}_i \cap {\mathcal {D}}_j\). If both \(g_{12}\) and \(g_{13}\) are rotations around O, then the tiling is clearly rotationally generated. Hence, assume that one of \(g_{12}\) and \(g_{13}\), say \(g_{12}\) is a reflection about a line \(\ell \) through O. Then, \(g_{12}({\mathcal {C}}_{13} \cup {\mathcal {C}}_{12}) = {\mathcal {C}}_{12} \cup {\mathcal {C}}_{23}\) yields that \({\mathcal {C}}_{12}\) is a straight line segment in \(\ell \), which, by the congruence of the tiles, implies also that \(C_{ij}\) is a segment for all \(i \ne j\). Thus, also in this case, the tiling is rotationally generated, and the assertion follows.

4 Remarks and Open Problems

First, we observe that the quantity \(n({\mathcal {K}})\) can be similarly defined for any O-symmetric convex body \({\mathcal {K}}\) in \({\mathbb {R}}^d\) playing the role of \({\mathcal {B}}^2\). On the other hand, Theorem 1.1 cannot be generalized for any O-symmetric convex body even in the case \(d=2\). Indeed, dissecting a parallelogram into three congruent parallelograms with two lines parallel to a pair of sides of the parallelogram shows that there are O-symmetric plane convex bodies \({\mathcal {K}}\) with \(n({\mathcal {K}})=3\). This raises the question which O-symmetric convex bodies \({\mathcal {K}}\) satisfy \(n({\mathcal {K}}) > 3\).

Following [6], we generalize Question 1 for balls in arbitrary dimensions.

Question 4

Are there monohedral tilings of the closed unit ball \({\mathcal {B}}^d\) such that the center of the ball is not contained in all of the tiles? More specifically, what are the values of d for which it is possible?

We also raise the following, related problem:

Question 5

If \({\mathcal {B}}^2\) has a tiling with similar copies of some topological disc \({\mathcal {D}}\), does it follow that the tiles are congruent? Does it follow that \({\mathcal {B}}^2\) has a tiling with congruent copies of \({\mathcal {D}}\)? Do these properties hold under some additional assumption on the tiles, e.g., if they have piecewise analytic boundaries?

We should finally mention the divisibility problem, in which the topological conditions on the tiles are dropped: A subset of \({\mathbb {R}}^d\) is m-divisible if it can be decomposed into \(m\in {\mathbb {N}}\) mutually disjoint congruent subsets. It is proved that typical convex bodies are not divisible [14], but balls are not typical in this sense, and they are m-divisible for large values of m if d is divisible by three [9] or d is even [10].