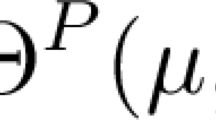Abstract
On the basis of the phase completion the notion of vertical and horizontal lifts of vector fields is defined in the tensor bundles over a Riemannian manifold. Such a tensor bundle is made into a manifold with a Riemannian structure of special type by endowing it with Sasakian metric. The components of the Levi-Civita and other metric connections with respect to Sasakian metrics on tensor bundles with respect to the adapted frame are presented. This having been done, it is shown that it is possible to study geodesics of Sasakian metrics dealing with geodesics of the base manifolds.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Cengiz N., Salimov A.A.: Diagonal lift in the tensor bundle and its applications. Appl. Math. Comput. 142, 309–319 (2003)
Cengiz N., Salimov A.A.: Complete lifts of derivations to tensor bundles. Bol. Soc. Mat. Mexiana 8(no. 1), 75–82 (2002)
L. A. Cordero, C. T. J. Dodson and M. de Leon, Differential geometry of frame bundles, Kluwer Acad. Pub., 1986.
Etayo F., Santamara R.: (J2 = ±1)-Metric manifolds. Publ. Math. Debrecen 57(no. 3-4), 435–444 (2000)
A. Gezer and A. A. Salimov, Diagonal lifts of tensor fields of type (1, 1) on crosssection in tensor bundles and its applications, J. KoreanMath. Soc. 45 (no. 2) (2008), 367–376.
A. Magden and A. A. Salimov, Horizontal lifts of tensor fields to sections of the tangent bundle, Russian Math. (Iz. VUZ.) 45 (no. 3) (2001), 73–76.
Mok K.P.: On differential geometry of frame bundles of Riemannian manifolds. J. reine angew. Math. 302, 16–31 (1976)
A. A. Salimov and N. Cengiz, Lifting of Riemannian metrics to tensor bundles, Russian Math. (IZ. VUZ.) 47 (no. 11) (2003), 47–55.
Salimov A.A., Iscan M., Etayo F.: Paraholomorphic B-manifold and its properties. Topology Appl. 154, 925–933 (2007)
Sasaki S.: On the differential geometry of tangent bundles of Riemannian manifolds. Tôhoku Math. J. 10, 338–358 (1958)
Yano K., Ishihara S.: Tangent and Cotangent bundles. Marcel Dekker, Inc, New York (1973)
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to the memory of Vladimir Vishnevskii (1929-2007)
This paper is supported by The Scientific and Technological Council of Turkey (TBAG-108T590)
Rights and permissions
About this article
Cite this article
Salimov, A.A., Gezer, A. & Akbulut, K. Geodesics of Sasakian Metrics on Tensor Bundles. Mediterr. J. Math. 6, 135–147 (2009). https://doi.org/10.1007/s00009-009-0001-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00009-009-0001-z