Analysis of a nonlinear magnetic levitation system vibrations controlled by a time-delayed proportional-derivative controller

Abstract

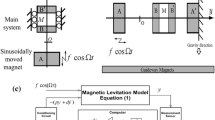
A time-delayed proportional-derivative controller is proposed in this paper to reduce the horizontal vibration of a magnetically levitated system having quadratic and cubic nonlinearities to primary and parametric excitations. Applying multiple scales perturbation technique, a second-order approximate solution is sought to analyze the nonlinear behavior of the system. The effects of the time delay are studied to indicate the stable range of time delays for the best performance. The results are compared with the numerical simulations, and this shows a good verification for the approximate solution and for the control algorithm used in this paper. A comparison with previously published work is included at the end.

Appendix

$$\begin{aligned} \zeta _{1}&= -\frac{5}{16}\alpha _{2}^{2} \alpha _{3} +\frac{9}{64}\alpha _{3}^{2} +\frac{25}{144}\alpha _{2}^4 \\ \zeta _{2}&= \frac{5}{6}\sigma _{1} \alpha _{2}^{2} -\frac{3}{4}\sigma _{1} \alpha _{3} -\frac{5}{12}p\alpha _{2}^{2} \cos \tau _{1}\\&+\,\frac{3}{8}d\alpha _{3} \sin \tau _{2} -\frac{5}{12}d\alpha _{2}^{2} \sin \tau _{2} +\frac{3}{8}p\alpha _{3} \cos \tau _{1} \\ \zeta _{3}&= \sigma _{1} ^{2}+\mu ^{2}+\frac{1}{4}p^{2}+\frac{1}{4}d^{2}-\frac{1}{2}pd\sin (\tau _{1} -\tau _{2} )\\&-\,\mu p\sin \tau _{1} +\mu d\cos \tau _{2} \\&-\,\sigma _{1} d\sin \tau _{2} -\sigma _{1} p\cos \tau _{1} \\ \\ \zeta _4&= -(\frac{k_{1} f_{1} }{2}+\frac{f_{1t} }{4})^{2} \\ \delta _{1}&= \frac{\left( {2k_{1} f_{1} \sin \varphi _{0} +f_t \sin \varphi _{0} +4\mu a_{0} -2pa_{0} \sin \tau _{1} +2da_{0} \cos \tau _{2} } \right) }{4a_{0} } \\ \delta _{2}&= \frac{\left( {2k_{1} f_{1} +f_t } \right) }{48a_{0}^{2} }\\&\times \left( {\begin{array}{l} -10\alpha _{2} ^{2}a_{0} ^{3}\cos \varphi _{0} +9\alpha _{3} a_{0} ^{3}\cos \varphi _{0} +6k_{1} f_{1} \cos ^{2}\varphi _{0} \\ \quad +3f_t \cos ^{2}\varphi _{0} +12\mu a_{0} \sin \varphi _{0} -6pa_{0} \sin \tau _{1} \sin \varphi _{0} \\ \quad +6da_{0} \cos \tau _{2} \sin \varphi _{0} \\ \end{array}} \right) \\ \rho _{1}&= \frac{25}{144}\alpha _{2}^4 +\frac{9}{64}\alpha _{3}^{2} -\frac{5}{16}\alpha _{2}^{2} \alpha _{3} \\ \rho _{2}&= \frac{3}{8}p\alpha _{3} \cos \tau _{1} -\frac{5}{12}d\alpha _{2}^{2} \sin \tau _{2} -\frac{3}{8}\sigma _{2} \alpha _{3} \\&-\,\frac{5}{12}p\alpha _{2}^{2} \cos \tau _{1} +\frac{5}{12}\sigma _{2} \alpha _{2}^{2} +\frac{3}{8}d\alpha _{3} \sin \tau _{2} \\ \rho _{3}&= \frac{1}{4}\sigma _{2} ^{2}+\mu ^{2}+\frac{1}{4}p^{2}+\frac{1}{4}d^{2}-\frac{1}{2}pd\sin (\tau _{1} -\tau _{2} )\\&-\,\mu p\sin \tau _{1} +\mu d\cos \tau _{2} \\&-\,\frac{1}{2}\sigma _{2} p\cos \tau _{1} -\frac{1}{2}\sigma _{2} d\sin \tau _{2} -\left[ {\frac{k_{2} f_{1} }{2}-\frac{\alpha _{2} k_{1} f_{1} }{2(1-\Omega ^{2})}} \right] ^{2} \\ \\ \eta _{1}&= \frac{1}{2(1-\Omega ^{2})}\left( {\begin{array}{l} k_{2} f_{1} \sin \varphi _{0} -k_{2} f_{1} \Omega ^{2}\sin \varphi _{0} -\alpha _{2} k_{1} f_{1} \sin \varphi _{0} \\ +2\mu -2\mu \Omega ^{2}-p\sin \tau _{1} +p\Omega ^{2}\sin \tau _{1} +d\cos \tau _{2} \\ -d\Omega ^{2}\cos \tau _{2} \end{array}} \right) \\ \end{aligned}$$

$$\begin{aligned} \eta _{2}&= \frac{k_{2} f_{1} -{k}_{2} f_{1} \Omega ^{2}-\alpha _{2} k_{1} f_{1} }{12(1-\Omega ^{2})^{2}}\left( {\begin{array}{l} -10\alpha _{2} ^{2}a_{0} ^{2}\cos \varphi _{0} +10\alpha _{2} ^{2}\Omega ^{2}a_{0} ^{2}\cos \varphi _{0} +9\alpha _{3} a_{0} ^{2}\cos \varphi _{0} \\ \quad -9\alpha _{3} \Omega ^{2}a_{0} ^{2}\cos \varphi _{0} -12\mu \Omega ^{2}\sin \varphi _{0} -6p\sin \tau _{1} \sin \varphi _{0} \\ \quad +12\mu \sin \varphi _{0} +6p\Omega ^{2}\sin \tau _{1} \sin \varphi _{0} +6d\cos \tau _{2} \sin \varphi _{0} \\ \quad -6d\Omega ^{2}\cos \tau _{2} \sin \varphi _{0} -6k_{2} f_{1} \sin ^{2}\varphi _{0} +6k_{2} f_{1} \Omega ^{2}\sin ^{2}\varphi _{0} \\ \quad +\,6\alpha _{2} k_{1} f_{1} \sin ^{2}\varphi _{0} \\ \end{array}} \right) \end{aligned}$$