Skip to main content
SpringerLink
Log in

Generalizations and Applications of the Lagrange Implicit Function Theorem

  • Published:
The Journal of the Astronautical Sciences Aims and scope Submit manuscript

Abstract

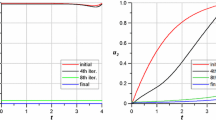
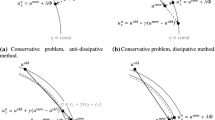
The implicit function theorem due to Lagrange is generalized to enable high order implicit rate calculations of general implicit functions about pre-computed solutions of interest. The sensitivities thus calculated are subsequently used in determining neighboring solutions about an existing root (for algebraic systems) or trajectory (in case of dynamical systems). The generalization to dynamical systems, as a special case, enables the calculation of high order time varying sensitivities of the solutions of boundary value problems with respect to the parameters of the system model and/or functions describing the boundary condition. The generalizations thus realized are applied to various problems arising in trajectory optimization. It was found that useful information relating the neighboring extremal paths can be deduced from these implicit rates characterizing the behavior in the neighborhood of the existing solutions. The accuracy of solutions obtained is subsequently enhanced using an averaging scheme based on the Global Local Orthogonal Polynomial (GLO-MAP) weight functions developed by the first author to blend many local approximations in a continuous fashion. Example problems illustrate the wide applicability of the presented generalizations of Lagrange’s classical results to static and dynamic optimization problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Hale, J. K. Ordinary Differential Equations, Pure and Applied Mathematics, ed. R. Courant, Bers, L., Stoker, J. J., Vol. XXI, 1969, New York, NY, Wiley-Interscience.

  2. Lagrange, J.L. Nouvelle Methode Pour Resoudre Les Equations Litterales (Pare le moten des series), in Euvres de Lagrange, 1770, Gauthier — Villars, Imperium — Libraire: Paris.

    Google Scholar 

  3. Dunyak, J. P., Junkins, J. L., and Watson, L. T. “Robust Nonlinear Least Squares Estimation Using the Chow-Yorke Homotopy Method,” Journal of Guidance, Control and Dynamics, 1984, Vol. 7, No. 6, pp. 752–753.

    Article  MATH  Google Scholar 

  4. Krantz, S.G. and Parks, H.R. The Implicit Function Theorem: History, Theory and Applications, 2002, Boston, MA, Birkhauser.

    MATH  Google Scholar 

  5. Bryson, A.E. and Ho, Y.C. Applied Optimal Control: Optimization, Estimation and Control, Revised Printing ed. 1975, Washington, DC, Hemisphere Publishing Corporation.

    Google Scholar 

  6. Tapley, B.D., Schutz, B.E., and Born, G.H. Statistical Orbit Determination, Elsevier Science and Technology Books, April, 2004, Burlington, MA, Elsevier Academic Press.

    Google Scholar 

  7. Beir Man, G. J. Factorization Methods for Discrete Sequential Estimation, Dover Reprints, 2008, Mineola, NY, Dover Publications.

    Google Scholar 

  8. Lim, K.B., Junkins, J.L., and Wang, B.P. “Re-Examination of Eigenvector Derivatives,” Journal of Guidance, Control and Dynamics, 1987, Vol. 10, No. 6, pp. 581–587.

    Article  MATH  Google Scholar 

  9. Junkins, J.L. and Kim, Y. “First and Second Order Sensitivity of the Singular Value Decomposition,” The Journal of the Astronautical Sciences, 1990, Vol. 38, No. 1, pp. 69–86.

    Google Scholar 

  10. Junkins, J.L. and Kim, Y. Introduction to Dynamics and Control of Flexible Structures, AIAA Education Series, ed. J.S. Przemieniecki, 1992, Washington, D.C., AIAA, Inc.

  11. Malanowski, K. and Maurer, H. “Sensitivity Analysis for Parametric Control Problems with Control State Constraints,” Computational Optimization and Applications, 1996, Vol. 5, pp. 253–283.

    Article  MathSciNet  MATH  Google Scholar 

  12. Malanowski, K. and Maurer, H. “Sensitivity Analysis for Optimal Control Problems Subject to Higher Order State Constraints,” Annals of Operations Research, 2001, Vol 101, pp. 43–73.

    Article  MathSciNet  MATH  Google Scholar 

  13. De Pinho, M.D.R. and Rosenblueth, J. “Mixed Constraints in Optimal Control: An Implicit Function Theorem Approach,” IMA Journal of Mathematical Control and Information, 2007, Vol. 24, pp. 197–218.

    Article  MathSciNet  MATH  Google Scholar 

  14. Castillo, E., Conejo, A. J., and Aranda, E. “Sensitivity Analysis in Calculus of Variations: Some Applications,” SIAM Review, 2008, Vol. 50, No. 2, pp. 294–312.

    Article  MathSciNet  MATH  Google Scholar 

  15. Chicone, C. Ordinary Differential Equations with Applications, Texts in Applied Mathematics, ed. J.E. Marsden, Sirovich, L., and Antman, S.S. 2006, New York, NY, Springer Publishing Company.

  16. Moulton, F.R. Differential Equations, 1930, New York, Macmillan Company.

    MATH  Google Scholar 

  17. Majji, M., Turner, J.D., and Junkins, J.L. “High Order Methods for Estimation of Dynamic Systems,” The Journal of the Astronautical Sciences, Vol. 57, Nos. 1 & 2, 2009.

    Google Scholar 

  18. Singla, P. and Junkins, J.L. Multi-Resolution Methods for Modeling and Control of Dynamical Systems, Applied Mathematics and Nonlinear Science, In Press, 2008, Boca-Raton, FL, CRC Press/ Chapman Hall.

    Book  Google Scholar 

  19. Battin, R. H. An Introduction to Mathematics and Methods of Astrodynamics, AIAA Education Series, ed. J.S. Przemieniecki 1999, Reston, VA, American Institute of Aeronautics and Astronautics, p. 786.

  20. Markley, F.L. “Kepler Equation Solver,” Celestial Mechanics and Dynamical Astronomy, 1995, Vol. 63, pp. 115–300.

    Article  MathSciNet  Google Scholar 

  21. Mortari, D. and Clocchiatti, A. “Solving Kepler’s Equation using Bezier Curves,” Celestial Mechanics and Dynamical Astronomy, 2007, Vol. 99, No. 1, pp. 45–57.

    Article  MathSciNet  MATH  Google Scholar 

  22. Abraham, R., Ratiu, T., and Marsden, J.E. Manifolds, Tensor Analysis and Applications, 2nd ed., Applied Mathematical Sciences, 2001, New York, Springer — Verlag.

    Google Scholar 

  23. Nah, R.S., Vadali, S.R., and Braden, E. “Fuel-Optimal, Low Thrust, Three-Dimensional Earth — Mars Trajectories,” Journal of Guidance, Control and Dynamics, 2001, Vol. 24, No. 6, pp. 1100–1107.

    Article  Google Scholar 

  24. Bate, R.R., Mueller, D.D., and White, J.E. Fundamentals of Astrodynamics, Dover Books on Astronomy. 1971, New York, NY, Dover Publications.

    Google Scholar 

  25. Junkins, J.L., Singla, P., Mortari, D., Bottke, W., and Durda, D. “A Study of Six Near Earth Asteroids,” Proceedings of the International Conference on Computational and Experimental Engineering and Sciences, 2005, Chennai, India.

  26. Davis, J., Singla, P., and Junkins, J.L. “Identifying Near-Term Missions and Impact Keyholes for Asteroid 99942 Apophis,” in Proceedings of the 7th Cranfield Conference on Dynamics and Control of Systems and Structures in Space, 2006, Old Royal Naval College, Greenwich, UK, Cranfield University Press.

  27. Majji, M., Junkins, J.L., and Turner, J.D. “Implicit Function Theorem and a Class of Two Point Boundary Value Problems,” Journal of Guidance, Control and Dynamics, 2009. Submitted and in review.

  28. Rauwolf, G.A., and Coverstone-Carroll, V.L. “Near-Optimal Low-Thrust Orbit Transfers Generated by a Genetic Algorithm,” Journal of Spacecraft and Rockets, 1996, Vol. 33, No. 6, pp. 859–862.

    Article  Google Scholar 

  29. Bader, B. W. and Kolda, T. G. “Algorithm 862: MATLAB Tensor Classes for Fast Algorithm Prototyping,” ACM Transactions on Mathematical Software, 2006, Vol. 32, No. 4, pp. 635–653.

    Article  MathSciNet  MATH  Google Scholar 

  30. Graham, A. Kronecker Products and Matrix Calculus with Applications, Ellis Horwood Series: Mathematics and its Applications, ed. G.M. Bell, 1981, New York, NY, John Wiley & Sons.

  31. Rauhala, U.A. “Array Algebra Expansion of Matrix and Tensor Calculus: Part 1,” SIAM Journal of Matrix Analysis and Applications, 2002, Vol. 24, No. 2, pp. 490–508.

    Article  MathSciNet  MATH  Google Scholar 

  32. Golub, G. H. and Vanloan, C. F. Matrix Computations, Johns Hopkins Studies in Mathematical Sciences, 1996, Baltimore, MD, The Johns Hopkins University Press.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Aerospace Engineering, Texas A&M University, College Station, TX, 77843-3141

    John L. Junkins (Regents Professor, Distinguished Professor, Royce E. Wisenbaker ’39 Chair in Engineering), James D. Turner (Research Professor, Director of Operations, Consortium of Autonomous Space Systems) & Manoranjan Majji (Ph.D. Candidate)

Authors
  1. John L. Junkins
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. James D. Turner
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Manoranjan Majji
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to John L. Junkins.

Additional information

Presented at the F. Landis Markley Astronautics Symposium, Cambridge, Maryland, June 29–July 2, 2008.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Junkins, J.L., Turner, J.D. & Majji, M. Generalizations and Applications of the Lagrange Implicit Function Theorem. J of Astronaut Sci 57, 313–345 (2009). https://doi.org/10.1007/BF03321507

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF03321507

Keywords

Search

Navigation