Skip to main content
SpringerLink
Log in

Wavelets in statistics: A review

  • Published:
Journal of the Italian Statistical Society Aims and scope Submit manuscript

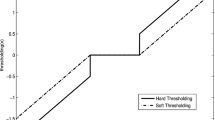
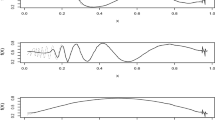
Abstract

The field of nonparametric function estimation has broadened its appeal in recent years with an array of new tools for statistical analysis. In particular, theoretical and applied research on the field of wavelets has had noticeable influence on statistical topics such as nonparametric regression, nonparametric density estimation, nonparametric discrimination and many other related topics. This is a survey article that attempts to synthetize a broad variety of work on wavelets in statistics and includes some recent developments in nonparametric curve estimation that have been omitted from review articles and books on the subject. After a short introduction to wavelet theory, wavelets are treated in the familiar context of estimation of «smooth» functions. Both «linear» and «nonlinear» wavelet estimation methods are discussed and cross-validation methods for choosing the smoothing parameters are addressed. Finally, some areas of related research are mentioned, such as hypothesis testing, model selection, hazard rate estimation for censored data, and nonparametric change-point problems. The closing section formulates some promising research directions relating to wavelets in statistics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abramovich, F., Sapatinas, T. andSilverman, B. W. (1998). Wavelet thresholding via a Bayesian approach. I. Royal Statist. Soc., Ser. B, part 4, 725–750.

    Article  MathSciNet  Google Scholar 

  2. Amato, U. andVuza, D. T. (1994). Wavelet Regularization for Smoothing Data. Technical report N. 108/94, Instituto per Applicazioni della Matematica, Napoli.

  3. Amato, U. andVuza, D. T. (1996). An Alternate Proof of a Result of Johnstone and Silverman concering Wavelet Thresholding Estimators for Data with Correlated Noise.Revue Roumaine Math. Pures Appi. 41, 431–438.

    MATH  MathSciNet  Google Scholar 

  4. Antoniadis, A. (1994). Smoothing noisy data with coiflets.Statistica Sinica 4 (2), 651–678.

    MATH  MathSciNet  Google Scholar 

  5. Antoniadis, A. (1994). Smoothing noisy data with tapered coiflets series.Scand. Journal of Statistics 23, 313–330.

    MathSciNet  Google Scholar 

  6. Antoniadis, A. andCarmona, R. (1991). Multiresolution analyses and wavelets for density estimation. Technical report, University of California, Irvine.

  7. Antoniadis, A., Grégoire, G. andMcKeague, I. (1994). Wavelet methods for curve estimation.J. Amer Statist. Assoc. 89 (428), 1340–1353.

    Article  MATH  MathSciNet  Google Scholar 

  8. Antoniadis, A. andPham, D. T. (1995). Wavelet regression for random or irregular design. Technical report. University of Grenoble.

  9. Antoniadis, A. andLavergne, C. (1995). Variance function estimation in regression with wavelet methods. In A. Antoniadis and G. Oppenheim (eds.),Wavelets and Statistics. Lecture Notes in Statistics,103, Springer-Verlag.

  10. Antoniadis, A., Grégoire, G. andVial, P. (1997a). Random design wavelet curve smoothing.Statistics and Prob. Letters, vol. 35, 225–232.

    Article  MATH  Google Scholar 

  11. Antoniadis, A., Gijbels, I. andGrégotre, G. (1997b). Model selection using wavelet decomposition and applications. Biometrika84 (4), 751–763.

    Article  MATH  MathSciNet  Google Scholar 

  12. Antoniadis, A., Grégoire, G. andNason, G. (1997c). Density and hazard rate estimation for right censored data using wavelet methods. Technical report. University of Grenoble.

  13. Antoniadis, A. andGijbels, I. (1997). Detecting abrupt changes by wavelet methods. Technical report. University of Grenoble.

  14. Averkamp, R. andHoudré, C. (1996). Wavelet thresholding for non (necessarily) Gaussian noise: a preliminary report. Technical report, Georgia Institute of Technology, Atlanta.

  15. Beran, R. (1994). Bootsrap variable selection and confidence sets. Technical report, University of California, Berkeley.

  16. Brillinger, D. R. (1994). Some River Wavelets.Environmetrics 5, 2 11–220.

    Google Scholar 

  17. Brillinger, D.R. (1995). Some Uses of Cumulants in Wvelet Analysis.J. Nonparam. Statistics 4.

  18. Bruce, A. G. andGao, H.-Y. (1194).S + Wavelets, Users manual. StatSci, Seatle.

  19. Bruce, A. G. andGao, H.-Y. (1996). Understanding WaveShrink: Variance and Bias Estimation. Biometrika83 (4), 727–746.

    Article  MATH  MathSciNet  Google Scholar 

  20. Bruce, A. G. andGao, H.-Y. (1997). WaveShink with firm shrinkage.Statistica Sinica, to appear.

  21. Buckhett, J. B. andDonoho, D. (1995). Wavelab and Reproducible research. In A. Antoniadis and G. Oppenheim (eds.),Wavelet and Statistics, Lecture Notes in Statistics,103, Springer-Verlag.

  22. Clyde, M. Parmigiani, G. andVidakovic, B. (1995). Multiple shrinkage and subset selection in wavelets. Technical report DP 95-37, Duke University.

  23. Chipman, H. A., Kolaczyj, E. D. andMcculloch, R. E. (1995). Adaptive Bayesian Wavelet Shrinkage. Technical report, University of Chicago.

  24. Chui, K. (1992).Wavelets: A Tutorial in Theory and Applications. Academic Press, Boston.

    MATH  Google Scholar 

  25. Cohen, A., Daubechies, I. andVial, P. (1993). Wavelets on the interval and fast wavelet transforms.Applied and Comp. Harmonic Analysis 1 (1), 54–81.

    Article  MATH  MathSciNet  Google Scholar 

  26. Cohen A. andRyan, R. D. (1995).Wavelets and Multiscale Signal Processing. Chapman & Hall, London.

    MATH  Google Scholar 

  27. Daubechies, I. (1992).Ten Lectures of Wavelets. CBMS-NSF regional conferences series in applied mathematics. SIAM, Philadelphia.

    Google Scholar 

  28. Daubechies, I. andLagarias, J. C. (1991). Two-scale difference equations: Existence and global regularity of solutions.SIAM Journal on Math. Analysis 22, 1388–1410.

    Article  MATH  MathSciNet  Google Scholar 

  29. Delyon, B. andJuditsky, A. (1996). On minimax wavelet estimators.Applied and Comp. Harmonic Analysis 3, 215–228.

    Article  MATH  MathSciNet  Google Scholar 

  30. DeVore, R. andLucier, B. J. (1992). Fast wavelet techniques for near-optimal signal processing. InIEEE Military Communication Conference, pp. 1129–1135.

  31. DeVore, R., Jawerth, B. andPoov, V. (1988). Interpolation of Besov spaces.Trans. Amer Math. Soc. 305, 397–414.

    Article  MATH  MathSciNet  Google Scholar 

  32. Donoho, D. L. (1994). Asymptotic risk for sup-norm loss: solution via optimal recovery. Prob.Theory and Related Fields 99, 145–170.

    Article  MATH  MathSciNet  Google Scholar 

  33. Donoho, D. L. andJohnstone, I. M. (1992). Minimax estimation via wavelet shrinkage. Technical report, Stanford University.

  34. Donoho, D. L. andJohnstone, I. M. (1994a). Ideal spatial adaptation by wavelet shrinkage.Biometrika 81, 425–455.

    Article  MATH  MathSciNet  Google Scholar 

  35. Donoho, D. L. andJohnstone, I. M. (1995). Adapting to unknown smoothness via wavelet shrinking.J. Am. Statist. Assoc. 90, 1200–1224.

    Article  MATH  MathSciNet  Google Scholar 

  36. Donoho, D. L. andJohnstone, I. M. (1994b). Ideal denoising in an orthonormal basis chosen from a library of bases.Compt. Rend. Acad. Sci. Paris A 319, 1317–1322.

    MATH  MathSciNet  Google Scholar 

  37. Donoho, D. L., Johnstone, I. M., Kerkyacharian, G. andPicard, D. (1995). Wavelet shrinkage: asymptotia (with discussion)?J. Roy. Statist. Soc., Ser. B 57(2), 301–370.

    MATH  MathSciNet  Google Scholar 

  38. Donoho, D. L., Johnstone, I. M., Kerkyacharian, G. andPicard, D. (1996). Density estimation by wavelet thresholding.Ann. Statist. 24 (2), 508–539.

    Article  MATH  MathSciNet  Google Scholar 

  39. Doukhan, P. (1990). Consistency of delta-sequence estimates of a density or of a regression function for a weakly dependent stationary sequence. Séminaire de Statistique d’Orsay, Université Paris Sud, 1991.

  40. Doukhan, P. andLéon, J. (1990). Déviation quadratique d’estimateurs de densité par projection orthogonale.Compt. Rend. Acad. Sci. Paris A 310, 424–430.

    Google Scholar 

  41. Engel, J. (1990). Density estimation with Haar series.Statistics and Probability Letters 9, 111–117.

    Article  MATH  MathSciNet  Google Scholar 

  42. Fan, J. (1996). Test of significance based on wavelet thresholding and Neyman’s truncation.J. Am. Statist. Assoc. 91, 674–688.

    Article  MATH  Google Scholar 

  43. Gao, H.-Y. (1993).Wavelet estimation of Spectral densities in Time series analysis. Ph. D. Thesis, University of California, Berkeley.

    Google Scholar 

  44. Gao, H.-Y. (1997). Wavelet Shrinkage Smoothing For Heteroscedastic Data. Technical report, ScatSci, Seatle.

  45. Gasser, T. andMüller, H. (1979). Kernel estimation of regression functions. In Gasser, T. and Müller, H. (eds.),Curve Estimation, Springer-Verlag, Heidelberg.

    Chapter  Google Scholar 

  46. Good, I. J. andGaskins, R. A. (1971). Density estimation and bump haunting by the penalized maximum likelihood method.J. Am. Statist. Assoc. 75, 42–69.

    Article  MathSciNet  Google Scholar 

  47. Hall, O. andNason, G. P. (1996). On choosing a non-integer resolution level when using wavelet methods. Technical report, University of Bristol.

  48. Hall, P. andPatil, P. (1995). On wavelet methods for estimating smooth functions.Bernoulli 1, 41–58.

    Article  MATH  MathSciNet  Google Scholar 

  49. Hall, P. andPatil, P. (1996a). Effect of threshold rules on performance of wavelet-based curve estimators.Statistica Sinica 6, 331–345.

    MATH  MathSciNet  Google Scholar 

  50. Hall, P. andPatil, P. (1996b). On the choice of smoothing parameter, threshold and truncation in nonparametric regression by nonlinear wavelet methods.J. Roy. Statist. Soc., Ser B 58, 361–377.

    MATH  MathSciNet  Google Scholar 

  51. Härdle, W. (1990).Applied nonparametric regression. Cambridge University Press, Cambridge.

    MATH  Google Scholar 

  52. Holschneider, M. (1995).Wavelets: An analysis tool. Clarendon Press, Oxford.

    MATH  Google Scholar 

  53. Jansen, M., Malfait, M. andBultheel, A. (1997). Generalized cross-validation for wavelet thresholding.Signal Processing,56 (1). To appear.

  54. Johnstone, I. M., Kerkyacharian, G. andPicard, D. (1992). Estimation d’une densité de probabilityé par méthode d’ondelettes.Compt. Rend. Acad. Sci. Paris A 315, 211–216.

    MATH  MathSciNet  Google Scholar 

  55. Johnstone, I. M. andSilverman, B. W. (1997). Wavelet threshold estimators for data with correlated noise.J. Roy. Statist. Soc., Ser B 59. In press.

  56. Kerkyacharian, G. andPicard, D. (1992). Density estimation in Besov Spaces.Statistics and Probability Letters 13, 15–24.

    Article  MATH  MathSciNet  Google Scholar 

  57. Kolaczyk, E. (1994).Wavelet methods for the inversion of some homogeneous linear operators in the presence of noisy data. Ph. D. Thesis, Stanford University.

  58. Mallat, S. G. (1989). A theory for multiresolution signal decomposition: the wavelet representation.IEEE Trans. on Pattern Analysis and Machine Intelligence 11, 674–693.

    Article  MATH  Google Scholar 

  59. Marron, S. J., Adak, S., Johnstone, I., Neumann, M. andPatil, P. (1997). Exact risk analysis of wavelet regression.Journal of Computational and Graphical Statistics. In press.

  60. Masry, E. (1994). Probability density estimation from dependent observations using wavelet orthonormal bases.Statistics and Probability Letters 21, 181–194.

    Article  MATH  MathSciNet  Google Scholar 

  61. Masry, E. (1996). Multivariate probabilty density estimation by wavelet methods: strong consistency and rates for stationary time series. Technical report, University of California, San Diego.

  62. Meyer, Y. (1990).Ondelettes et Opéerateurs I: Ondelettes. Hermann, Paris.

    Google Scholar 

  63. Michelli, C. A. andRivlin, T. J. (1975). A survey of optimal recovery. In Michelli, C. A. and Rivlin, T. J. (eds.),Optimal estimation in Approximating theory, pp. 1–54, Plenum, New York.

    Google Scholar 

  64. Müller, H. G. (1985). Empirical bandwidth choice for nonparametric kernel regression by means of pilot estimators.Statist. Decisions 2, 193–206.

    Google Scholar 

  65. Nason, G. P. (1996). Wavelet regression using cross-validation.J. Roy. Statist. Soc., Ser B 58, 463–479.

    MATH  MathSciNet  Google Scholar 

  66. Nason, G. J. (1995). Choice of the threshold parameter in wavelet function estimation. In A. Antoniadis and G. Oppenheim (eds.),Wavelets and Statistics, pp. 261–280, Lecture Notes in Statistics, Springer-Verlag, New York.

    Google Scholar 

  67. Nason, G. J. andSilverman, B. W. (1994). The discrete wavelet transform inS.Journal of Computational and Graphical Statistics 3, 163–191.

    Article  Google Scholar 

  68. Neumann, M. H. (1994). Spectral density estimation via nonlinear wavelet methods for stationary non-Gaussian series. Technical report 99, Institute for applied and stochastic analysis, Berlin.

  69. Neumann, M. H. andSpokoiny, V. G. (1993). On the efficiency of wavelet estimators under arbitrary error distributions.Discussion Paper No. 4, Hümboldt Universität zu Berlin.

  70. Ogden, T. R. (1996).Essential wavelets for statistical applications and data analysis. Birkhäuser, Basel.

    Google Scholar 

  71. Oudshoorn, C. (1994). Wavelet-based nonparametric regression: optimal rate in the sup-norm. Technical report848, University Utrecht.

  72. Penev, S. andDechevsky, L. (1997). On non-negative wavelet-based estimators. Technical report, University of New South Wales. To appear inJ. of Nonparam. Statistics.

  73. Pinheiro, A. andVidakovic, B. (1995). Estimating the square root of a density via compactly supported wavelets. Technical reportDP 95-14, Duke University.

  74. Potier, C. andVercken, C. (1994). Spline fitting Numerous Noisy Data with discontinuities. In Laurent et al. (eds.),Curves and Surfaces, pp. 477–480, Academic Press, New York.

    Google Scholar 

  75. Raimondo, M. (1996).Situations non ergodiques et utilisations de méthodes d’ondelettes. Ph. D. Thesis, University Paris 7.

  76. Ramlau-Hansen, H. (1983). Smoothing counting processes by means of kernel functions.Ann. Statist.11, 453–466.

    Article  MATH  MathSciNet  Google Scholar 

  77. Saito, N. (1994). Simultaneous noise suppression and signal compression using a library of orthonormal bases and the minimum description length criterion. In Foufoula-Georgiou, E. and Kumar, P. (eds.),Wavelets in Geophysics, Academic Press, New York.

    Google Scholar 

  78. Stein, C. (1981). Estimation of the mean of a multivariate normal distribution.Ann. Statist.10, 1135–1151.

    Article  Google Scholar 

  79. Sweldens, W. (1996). The lifting scheme: A custom-design construction of biorthogonal wavelets.Applied and Comp. Harmonic Analysis 3, 186–200.

    Article  MATH  MathSciNet  Google Scholar 

  80. Sweldens, W. (1996). The lifting scheme: A construction of second generation wavelets. Technical report 1995:6, Industrial Mathematics Initiative, Department of Mathematics, University of South Carolina.

  81. Triebel, H. (1992).Theory of function spaces II. Birkhäuser, Basel.

    Google Scholar 

  82. Tribouley, K. (1995). Practical estimation of multivariate density using wavelet methods.Statistica Neerlandica 49, 41–62.

    Article  MATH  MathSciNet  Google Scholar 

  83. Vannucci, M. andVidakovic, B. (1995). Preventing the Dirac disaster: wavelet based density estimation. Technical reportDP 95-24, Duke University.

  84. Vidakovic, B. (1994). Nonlinear wavelet shrinkage with Bayes rules and Bayes factors. Technical reportDP 94-24, Duke University.

  85. von Sachs, R. andSchneider, K. (1996). Wavelet smoothing of evolutionary spectra by nonlinear thresholding. Applied and Comp.Harmonic Analysis 3 (3), 268–282.

    Article  MATH  MathSciNet  Google Scholar 

  86. Wahba, G. (1990).Spline models for observational data. CBMS-NSF regional conferences series in applied mathematics. SIAM, Philadelphia.

    Google Scholar 

  87. Walter, G. G. (1992). Approximation of the Delta Function by Wavelets.J. Approx. Theory 71, 329–343.

    Article  MATH  MathSciNet  Google Scholar 

  88. Walter, G. O. (1994).Wavelets and Other Orthogonal Systems with Applications. CRC Press, Boca Raton, Florida.

    MATH  Google Scholar 

  89. Wang, Y. (1995). Jump and Sharp Cusp Detection by wavelets.Biometrika 82, 385–397.

    Article  MATH  MathSciNet  Google Scholar 

  90. Wang, Y. (1996). Function estimation via wavelet shrinkage for long-memory data.Ann. Statist.24 (2), 466–484.

    Article  MATH  MathSciNet  Google Scholar 

  91. Weyrich, N. andWarhola, O. T. (1995). Denoising using wavelets and cross-validation. IN Singh, S. P. (ed.),Approximation Theory, wavelet and applications, NATO ASI series C, pp. 523–532.

  92. Wickerhauser, M. V. (1994).Adapted Wavelet Analysis: From Theory to Software. AK Peters, Boston.

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratoire IMAG-LMC, University Joseph Fourier, BP 53, 38041, Grenoble Cedex 9, France

    A. Antoniadis

Authors
  1. A. Antoniadis
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Research supported by the IDOPT project (CNRS-INRIA-UJF-INPG). This paper, the following discussions and the reply by A. Antoniadis are the result of a seminar hold in Rome, in September 1997. The editorial board wants to thank ISTAT for its financial support.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Antoniadis, A. Wavelets in statistics: A review. J. Ital. Statist. Soc. 6, 97 (1997). https://doi.org/10.1007/BF03178905

Download citation

  • DOI: https://doi.org/10.1007/BF03178905

Keywords and phrares

Search

Navigation