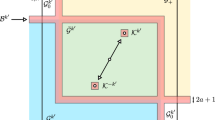
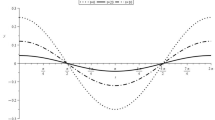
Abstract
We refine and generalize a symmetry-breaking bifurcation theorem by Werner and Spence [14]. Our theorem is so simple that we can apply it to the numerical verification for the bifurcation phenomena, for example, in non-linear vibration described by a semilinear wave equation. The point of our refinement is that the simplicity condition on (the candidate of) a bifurcation point in the original theorem is replaced by the regularity condition of a certain map, which is an easier condition to check. Our generalization enables us to apply the theorem directly to non-Fréchet differentiable maps and makes the computational process simple. For the same purpose we also generalize some basic functional analytical theorems such as the convergence theorem of Newton’s method and implicit function theorems.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
M.G. Crandall and P.H. Rabinowitz, Bifurcation from simple eigenvalues. J. Funct. Anal.,8 (1971), 321–340.
J.G. Heywood, W. Nagata and W. Xie, A numerically based existence theorem for the Navier-Stokes equations. J. Math. Fluid. Mech.,1 (1999), 5–23.
T. Kawanago, Computer assisted proof to symmetry-breaking bifurcation phenomena in nonlinear vibration. Japan J. Indust. Appl. Math.,21 (2004), 75–108.
Y. Komatsu, A bifurcation phenomenon for the periodic solutions of a semilinear dissipative wave equation. J. Math. Kyoto Univ.,41 (2001), 669–692.
A. Matsumura, Bifurcation phenomena for the Duffing equation. Advances in Nonlinear Partial Differential Equations and Stochastics (eds. Kawashima and Yanagisawa), World Scientific, 1998.
T. Nishida, Y. Teramoto and H. Yoshihara, Bifurcation problems for equations of fluid dynamics and computer aided proof. Lecture Notes in Numer. Appl. Anal.14, Springer, 1995, 145–157.
S. Oishi, Introduction to Nonlinear Analysis (in Japanese). Corona-sha, 1997.
S. Oishi, Numerical verification of existence and inclusion of solutions for nonlinear operator equations. J. Comput. Appl. Math.,60 (1995), 171–185.
M. Plum, Enclosures for two-point boundary value problems near bifurcation points. Scientific Computing and Validated Numerics (Wuppertal, 1995), Math. Res.90, Akademie Verlag, Berlin, 1996, 265–279.
P.H. Rabinowitz, Periodic solutions of non-linear hyperbolic partial differential equations. Comm. Pure Appl. Math.,20 (1967), 145–205.
Y. Shinohara, A geometric method of numerical solution of nonlinear equations and error estimation by Urabe’s proposition. Publ. RIMS Kyoto Univ.,5 (1969), 1–9.
T. Tsuchiya, Numerical verification of simple bifurcation points. RIMS Kokyuroku831 (1993), 129–140.
T. Tsuchiya and M.T. Nakao, Numerical verification of solutions of parametrized nonlinear boundary value problems with turning points. Japan J. Indust. Appl. Math.,14 (1997), 357–372.
B. Werner and A. Spence, The computation of symmetry-breaking bifurcation point. SIAM J. Numer. Anal.,21 (1984), 388–399.
M. Urabe, Galerkin’s procedure for nonlinear periodic systems. Arch. Rat. Mech. Anal.,20 (1965), 120–152.
Author information
Authors and Affiliations
Corresponding author
Additional information
Dedicated to Professors Takaaki Nishida and Masayasu Mimura on their sixtieth birthdays
An erratum to this article is available at http://dx.doi.org/10.1007/BF03167481.
About this article
Cite this article
Kawanago, T. A symmetry-breaking bifurcation theorem and some related theorems applicable to maps having unbounded derivatives. Japan J. Indust. Appl. Math. 21, 57–74 (2004). https://doi.org/10.1007/BF03167432
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF03167432