Skip to main content
SpringerLink
Log in

Exact penalization and stationarity conditions of mathematical programs with equilibrium constraints

  • Published:
Mathematical Programming Submit manuscript

Abstract

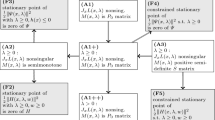
Using the theory of exact penalization for mathematical programs with subanalytic constraints, the theory of error bounds for quadratic inequality systems, and the theory of parametric normal equations, we derive various exact penalty functions for mathematical programs subject to equilibrium constraints, and we also characterize stationary points of these programs.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. E. Aiyoshi and K. Shimizu, “A solution method for the static constrained Stackelberg problem via penalty method”,IEEE Transactions on Automatic Control AC-29 (1984) 1111–1114.

    Article  MATH  MathSciNet  Google Scholar 

  2. G. Anandalingam and T. Friesz, eds. “Hierarchical optimization”,Annals of Operations Research 34 (1992).

  3. G. Anandalingam and D.J. White, “A solution method for the linear static Stackelberg problem using penalty function”,IEEE Transactions on Automatic Control 35 (1990) 1170–1173.

    Article  MATH  MathSciNet  Google Scholar 

  4. J.P. Aubin and H. Frankowska,Set-Valued Analysis (Birkäuser, Boston, 1990).

    MATH  Google Scholar 

  5. J.F. Bard, “An algorithm for solving the general bilevel programming problem”,Mathematics of Operations Research 8 (1983) 260–272.

    MATH  MathSciNet  Google Scholar 

  6. J.F. Bard, “Optimality conditions for the bilevel programming problem”,Naval Research Logistics Quarterly 31 (1984) 13–26.

    MATH  MathSciNet  Google Scholar 

  7. J.F. Bard, “Convex two-level optimization”Mathematical Programming 40 (1988) 15–27.

    Article  MATH  MathSciNet  Google Scholar 

  8. Z. Bi, P. Calamai, and A. Conn, “An exact penalty function approach for the linear bilevel programming problem”, Working paper. Department of Systems Design and Engineering, University of Waterloo, Waterloo, (1991).

    Google Scholar 

  9. E. Bierstone and P.D. Milman, “Semianalytic and subanalytic sets”,Institut des Hautes Etudes Scientifiques, Publications Mathématiques 67 (1988) 5–42.

    MATH  MathSciNet  Google Scholar 

  10. J.V. Burke, “An exact penalization viewpoint of constrained optimization”,SIAM Journal on Control and Optimization 29 (1991) 968–998.

    Article  MATH  MathSciNet  Google Scholar 

  11. R.W. Chaney, “PiecewiseC k functions in nonsmooth analysis”,Nonlinear Analysis, Theory, Methods & Applications 15 (1990) 649–660.

    Article  MATH  MathSciNet  Google Scholar 

  12. F.H. Clarke,Optimization and Nonsmooth Analysis (Wiley, New York, 1983).

    MATH  Google Scholar 

  13. R.W. Cottle, J.S. Pang, and R.E. Stone,The Linear Complementarity Problem (Academic Press, Boston, 1992).

    MATH  Google Scholar 

  14. J.P. Dedieu, “Penalty functions in subanalytic optimization”,Optimization 26 (1992) 27–32.

    MATH  MathSciNet  Google Scholar 

  15. S. Dempe, “A necessary and a sufficient optimality condition for bilevel programming problems”,Optimization 25 (1992) 341–354.

    MATH  MathSciNet  Google Scholar 

  16. B.C. Eaves, “On the basic theorem of complementarity”,Mathematical Programming 1 (1971) 68–75.

    Article  MATH  MathSciNet  Google Scholar 

  17. A.V. Fiacco,Introduction to Sensitivity and Stability Analysis in Nonlinear Programming (Academic Press, New York, 1993).

    Google Scholar 

  18. J. Gauvin, “A necessary and sufficient regularity condition to have bounded multipliers in nonconvex programming”,Mathematical Programming 12 (1977) 136–138.

    Article  MATH  MathSciNet  Google Scholar 

  19. M.S. Gowda and J.S. Pang, “Stability analysis of variational inequalities and nonlinear complementarity problems”,Mathematics of Operations Research 19 (1994) 831–879.

    Article  MATH  MathSciNet  Google Scholar 

  20. M. Guignard, “Generalized Kuhn-Tucker conditions for mathematical programming problems in a Banach Space”,SIAM Journal on Control 7 (1969) 232–241.

    Article  MATH  MathSciNet  Google Scholar 

  21. P.T. Harker and J.S. Pang, “On the existence of optimal solutions to mathematical program with equilibrium constraints”,Operations Research Letters 7 (1988) 61–64.

    Article  MATH  MathSciNet  Google Scholar 

  22. H. Hironaka, “Introduction to real-analytic sets and real-analytic maps”, Istituto Matematico “L. Tonelli” dell' Università de Pisa, Italy (1973).

    Google Scholar 

  23. A.J. Hoffman, “On approximate solutions of systems of linear inequalities”,Journal of Research of the National Bureau of Standards 49 (1952) 263–265.

    MathSciNet  Google Scholar 

  24. R. Janin, “Directional derivative of the marginal function in nonlinear programming”,Mathematical Programming Study 21 (1984) 110–126.

    MATH  MathSciNet  Google Scholar 

  25. M. Kojima, “Strongly stable stationary solutions in nonlinear programs”, in: S.M. Robinson, ed.,Analysis and Computation of Fixed Points, (Academic Press, New York 1980) pp 93–138.

    Google Scholar 

  26. J. Kyparisis, “On uniqueness of Kuhn-Tucker multipliers in nonlinear programming”,Mathematical Programming 32 (1985) 242–246.

    Article  MATH  MathSciNet  Google Scholar 

  27. N.G. Lloyd,Degree Theory (Cambridge University Press Cambridge, 1978).

    MATH  Google Scholar 

  28. M.S. Lojasiewicz, “Sur le problème de la division”,Studia Mathematica 18 (1959) 87–136.

    MATH  MathSciNet  Google Scholar 

  29. M.S. Lojasiewicz, “Ensembles semi-analytiques”, Institut des Hautes Etudes Scientifiques, Bures-sur-Yvette (1964).

    Google Scholar 

  30. Z.Q. Luo and J.S. Pang, “Error bounds for analytic systems and their applications”,Mathematical Programming 67 (1994) 1–28.

    Article  MathSciNet  Google Scholar 

  31. O.L. Mangasarian,Nonlinear Programming (McGraw-Hill, New York, 1969).

    MATH  Google Scholar 

  32. O.L. Mangasarian, “Sufficiency of exact penalty minimization”,SIAM Journal on Control and Optimization 23 (1985) 30–37.

    Article  MATH  MathSciNet  Google Scholar 

  33. O.L. Mangasarian “A simple characterization of solution sets of convex program”,Operations Research Letters 7 (1988) 21–26.

    Article  MATH  MathSciNet  Google Scholar 

  34. O.L. Mangasarian and S. Fromovitz, “The Fritz John optimality necessary conditions in the presence of equality and inequality constraints”,Journal of Mathematical Analysis and Applications 17 (1967) 37–47.

    Article  MATH  MathSciNet  Google Scholar 

  35. P. Marcotte, “Network design problem with congestion effects: A case of bilevel programming”,Mathematical Programming, 34 (1986) 142–162.

    Article  MATH  MathSciNet  Google Scholar 

  36. P. Marcotte and D.L. Zhu, “Exact and inexact penalty methods for the generalized bilevel programming problems”, Publication #920, Centre de Recherche sur les Transports, Université de Montréal, Montréal, Québec, Canada (1993).

    Google Scholar 

  37. J.M. Ortega and W.C. Rheinboldt,Iterative Solution of Nonlinear Equations in Several Variables (Academic Press, New York, 1970).

    MATH  Google Scholar 

  38. J.V. Outrata, “On optimization problems with variational inequality constraints”,SIAM Journal of Optimization 4 (1994) 340–357.

    Article  MATH  MathSciNet  Google Scholar 

  39. J.S. Pang, “Newton's method for B-differentiable equations”Mathematics of Operations Research 15 (1990) 311–341.

    MATH  MathSciNet  Google Scholar 

  40. J.S. Pang, “Complementarity problems”, in: R. Horst and P. Pardalos, eds.,Handbook on Global Optimization (Kluwer Academic Publishers, Dordrecht/Boston, 1994), pp. 271–338.

    Google Scholar 

  41. J.S. Pang, “A degree-theoretic approach to parametric nonsmooth equations with multivalued perturbed solution sets”,Mathematical Programming, Series B 62 (1993) 359–384.

    Article  Google Scholar 

  42. J.S. Pang and D. Ralph, “Piecewise smoothness, local invertibility, and parametric analysis of normal maps”,Mathematics of Operations Research 21 (1996) 401–426.

    MATH  MathSciNet  Google Scholar 

  43. D. Ralph and S. Dempe, “Directional derivatives of the solution of a parametric nonlinear program”, Manuscript, Department of Mathematics, University of Melbourne, Australia (1994).

    Google Scholar 

  44. S.M. Robinson, “Strongly regular generalized equations”,Mathematics of Operations Research 5 (1980) 43–62.

    MATH  MathSciNet  Google Scholar 

  45. S.M. Robinson, “Some continuity properties of polyhedral multifunctions”,Mathematical Programming Study 14 (1981) 206–214.

    MATH  Google Scholar 

  46. S.M. Robinson, “Generalized equations and their applications, part II: applications to nonlinear programming”,Mathematical Programming Study 19 (1982) 200–221.

    MATH  Google Scholar 

  47. S.M. Robinson, “Local structure of feasible sets in nonlinear programming, Part III: Stability and sensitivity”,Mathematical Programming Study 30 (1987) 45–66. Corrigenda,Mathematical Programming 49 (1987) 143.

    MATH  Google Scholar 

  48. S.M. Robinson, “An implicit-function theorem for a class of nonsmooth functions”,Mathematics of Operations Research 16 (1991) 292–309.

    MATH  MathSciNet  Google Scholar 

  49. S.M. Robinson, “Normal maps induced by linear transformations”,Mathematics of Operations Research 17 (1992) 691–714.

    MATH  MathSciNet  Google Scholar 

  50. H. Van Stackelberg,The Theory of Market Economy (Oxford University Press, 1952).

  51. J. Warga, “A necessary and sufficient condition for a constrained minimum”,SIAM Journal on Optimization 2 (1992) 665–667.

    Article  MATH  MathSciNet  Google Scholar 

  52. J.J. Ye and D.L. Zhu, “Optimality conditions for bilevel programming problems”, DMS-6180IR, Department of Mathematics and Statistics, University of Victoria, Victoria, B.C., Canada (1993).

    Google Scholar 

  53. J.J. Ye, D.L. Zhu, and Q. Zhu, “Generalized bilevel programming problem”, manuscript. Department of Mathematics and Statistics, University of Victoria, Victoria, B.C., Canada (1993).

    Google Scholar 

  54. R. Zhang, “Problems of hierarchical optimization: Nonsmoothness and analysis of solutions”, Ph.D. dissertation, Department of Applied Mathematics, University of Washington, Seattle (1990).

    Google Scholar 

  55. R. Zhang, “Problems of hierarchical optimization in finite dimensions”,SIAM Journal on Optimization 4 (1994) 521–536.

    Article  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Communications Research Laboratory, McMaster University, Room 225, L8S 4K1, Hamilton, Ont, Canada

    Zhi-Quan Luo

  2. Department of Mathematical Sciences, The Johns Hopkins University, 21218-2689, Baltimore, MD, USA

    Jong-Shi Pang

  3. Department of Mathematics, The University of Melbourne, 3052, Parkville, Vic., Australia

    Daniel Ralph

  4. Institute of Applied Mathematics, Academia Sinica, Beijing, People's Republic of China

    Shi-Quan Wu

Authors
  1. Zhi-Quan Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jong-Shi Pang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Daniel Ralph
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shi-Quan Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

The research of this author is based on work supported by the National Sciences and Engineering Research Council of Canada under grant OPG0090391.

The research of this author is based on work supported by the National Science Foundation under grants DDM-9104078 and CCR-9213739. Part of this paper was completed while he was visiting The University of Melbourne and The University of New South Wales.

The research of this author is based on work supported by the Australian Research Council.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Luo, ZQ., Pang, JS., Ralph, D. et al. Exact penalization and stationarity conditions of mathematical programs with equilibrium constraints. Mathematical Programming 75, 19–76 (1996). https://doi.org/10.1007/BF02592205

Download citation

  • Received:

  • Revised:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02592205

Keywords

Search

Navigation