Skip to main content
SpringerLink
Log in

Shallow-water equations with dispersion. Hyperbolic model

  • Published:
Journal of Applied Mechanics and Technical Physics Aims and scope

Abstract

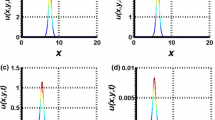
A hyperbolic shallow-water model is constructed with allowance for nonlinear and dispersive effects. The model describes solitonlike solutions in a range of wave velocities and predicts the breaking of smooth waves when the limiting amplitude is attained. The model is found to be adequate by comparison with experimental data on the evolution of a wave packet generated by the moving lateral wall of a channel.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G. B. Whitham,Linear and Nonlinear Waves, John Wiley and Sons, New York (1974).

    MATH  Google Scholar 

  2. V. E. Nakoryakov, “Hydrodynamics of two-phase flows,” in:Hydrodynamics and Heat Transfer in Two-Phase Media (Collected scientific papers) [in Russian], Inst. of Thermal Physics, Sib. Div., Acad. of Sci. of the USSR, Novosibirsk (1981).

    Google Scholar 

  3. S. L. Gavrilyuk and S. M. Shurgin, “Media with equations of state that depend on derivatives,”Prikl. Mekh. Tekh. Fiz.,37, No. 2, 35–49 (1996).

    MATH  Google Scholar 

  4. S. V. Iordanskii, “On the equations of motion of a liquid with gas bubbles,”Prikl. Mekh. Tekh. Fiz., No. 3, 102–110 (1960).

    MATH  Google Scholar 

  5. V. Yu. Liapidevskii, “Modeling of two-phase flows on the basis of conservation laws,” in:Dynamics of Continuous Media (Collected scientific papers) [in Russian], Novosibirsk,76 (1986), pp. 111–120.

  6. L. V. Ovsyannikov, N. I. Makarenko, V. I. Nalimov, et al.,Nonlinear Problems of the Theory of Surface and Internal Waves [in Russian], Nauka, Novosibirsk (1985).

    MATH  Google Scholar 

  7. V. I. Bukreev and N. P. Turanov, “Experiments with shallow-water waves generated by the motion of the lateral wall of a channel,”Prikl. Mekh. Tekh. Fiz.,37, No. 6, 44–50 (1996).

    Google Scholar 

  8. V. I. Bukreev, E. M. Romanov, and N. P. Turanov, “Breaking of gravity waves in the neighborhood of the second critical velocity of their propagation,”Prikl. Mekh. Tekh. Fiz.,39, No. 2, 52–58 (1998).

    MATH  Google Scholar 

  9. V. Yu. Liapidevskii and S. I. Plaksin, “Structure of shock waves in a gas-liquid medium with the nonlinear equation of state,” in:Dynamics of Continuous Media (Collected scientific papers) [in Russian], Novosibirsk,62 (1983), pp. 75–92.

  10. V. Yu. Liapidevskii, “Flow chocking in flowing about an obstacle by a two-layer mixed liquid,”Prikl. Mat. Mekh.,58, No. 4, 108–112 (1994).

    MathSciNet  Google Scholar 

Download references

Authors
  1. V. Yu. Liapidevskii
    View author publications

    You can also search for this author in PubMed Google Scholar

Additional information

Lavrent'ev Institute of Hydrodynamics, Siberian Division, Russian Academy of Sciences, Novosibirsk 630090. Translated from Prikladnaya Mekhanika i Tekhnicheskaya Fizika, Vol. 39, No. 2, pp. 40–46, March–April, 1998.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liapidevskii, V.Y. Shallow-water equations with dispersion. Hyperbolic model. J Appl Mech Tech Phys 39, 194–199 (1998). https://doi.org/10.1007/BF02468084

Download citation

  • Received:

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02468084

Keywords

Search

Navigation