Skip to main content
SpringerLink
Log in

A simple calculation of the transverse impact on beams and its experimental verification

Since central maximum loading on beams by transverse impact is independent of boundary conditions, the integral equation for impact force due to transverse impact can be simplified and thereby facilitate mechanical-loading calculations

  • Published:
Experimental Mechanics Aims and scope Submit manuscript

Abstract

The tests of several scientific workers have shown that the central maximum loading by transverse impact on beams is independent of the boundary conditions. In this case, the length of the beam is so long that the elastic waves reflected from the supports return to the point of contact after the central peak stress has developed. Now, by these conditions it is possible to simplify the integral equation for the impact force due to the transverse impact. The simplification is realized by calculating separately the series of the eigenfunctions and the eigenfrequencies. Introducing a special reference time and dimensionaless variables, the altered integral equation may be treated in a relative simple way by a computer. The results given in dimensionless form, namely the impact force and the central bending strain as a function of time, allow quickly the calculation of the mechanical loading. The magnitudes of the impact values also depend on a parameter which may be signified as a characteristic value of the transverse impact. This parameter contains the impact velocity, the striking mass, the Hertz constant and a parameter of the beam. This simplified theory of transverse impact was verified by measurements with strain gages, displacement device and PhotoStress method. The contact time was also measured and the data of the tests were changed, i.e., the velocity of the striking mass and the magnitude of the mass. In order to obtain the axial central strain at the lower side of the beam, the added action of the impact force must be taken into account according to the theory of Wilson-Stokes. Using the normalized curves of data of the impact, it is possible for untrained engineers to calculate the mechanical loading.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

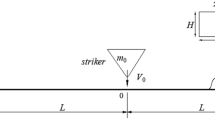
m :

mass of the striking body

M :

mass of the beam

μ:

mass of the beam per unit length

r :

radius of the spherical surface of the striking body

ρ:

density

L :

length of the beam

h :

height of the beam

d :

thickness of the beam

C b :

48EI/L 3

I :

moment of inertia (=1/12dh 3)

x :

coordinate coincident with neutral axis of the beam

x 0 :

point of contact (equalL/2)

W :

deflection of the beam (W 0 central deflection)

w :

displacement of the striking mass

(w-W 0):

relative approach of the colliding bodies

t,t′ :

time variables

T :

reference time

T k :

contact time

τ,τ′:

dimensionless time variables (t,T resp.t′/T)

σ:

dimensionless relative approach (w-W 0/Tv 0

K :

Hertz constant

ε:

strain

v 0 :

impact velocity of the striking mass

ω n :

eigenfrequency

C n :

eigenfunction

b n :

L/2 (especially by simple supported beams)

P :

impact force

\(\bar \lambda \) :

wavelength of the bending wave

c :

phase velocity of the bending waves

n :

ordinal number of the vibration

E :

Young's modulus

ν:

Poisson's ratio

α:

parameter of the beam

λ:

parameter of the impact

References

  1. Timoshenko, S., “Zur Frage nach der Wirkung eines Stoßes auf einen Balken,”Z. Math. Phys. 62,198–209 (1913).

    Google Scholar 

  2. Emschermann, H. H., and Rühl, K. “Beanspruchungen eines Biegeträgers bei schlagartiger Querbelatung,” VDI-Forschungsheft Nr. 443 (1954).

  3. Goldsmith, W., “Impact, the Theory and Physical Behavior of Colliding Solids,”Ed. Arnold Ltd., London, 278–279 (1960).

    Google Scholar 

  4. Eringen, A. C., “Transverse Impacton Beams and Plates,”Jnl. Appl. Mech.,20,461–468 (1953).

    Google Scholar 

  5. Zener, Cl., “The Intrinsic Inelasticity of Large Plates,”Phys. Rev.,59,669–673 (1941).

    Google Scholar 

  6. Boussinesq, J. N., “Application des Potentiels,” Paris, 486 (1885).

  7. Eschler, H., “Beitrag zur elementaren Theorie des Querstoßes auf Stäbe und Platten,”Ing. Arch.,12,31–37 (1941).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Deutsche Versuchsanstalt für Luft-und Raumfahrt E. V., Institut für Festigkeit, Mülheim-Ruhr, Flughafen, Germany

    Horst Schwieger

Authors
  1. Horst Schwieger
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Schwieger, H. A simple calculation of the transverse impact on beams and its experimental verification. Experimental Mechanics 5, 378–384 (1965). https://doi.org/10.1007/BF02326086

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1007/BF02326086

Keywords

Search

Navigation